Login/Sign Up
Home » Prove the result that the velocity v of translation of a rolling body (like a ring, disc, cylinder or sphere) at the bottom of an inclined plane of a height is given by using dynamical consideration (i.e. by consideration of forces and torques). Note is the radius of gyration of the body about its symmetry axis, and is the radius of the body. The body starts from rest at the top of the plane.
Prove the result that the velocity v of translation of a rolling body (like a ring, disc, cylinder or sphere) at the bottom of an inclined plane of a height h is given by \mathrm{v}^{2}=2 \mathrm{gh} /\left(1+\mathrm{k}^{2} / \mathrm{R}^{2}\right) using dynamical consideration (i.e. by consideration of forces and torques). Note \mathrm{k} is the radius of gyration of the body about its symmetry axis, and \mathbf{R} is the radius of the body. The body starts from rest at the top of the plane.
CBSE | Class 11 | NCERT | Physics | System of Particles and Rotational Motion
Prove the result that the velocity v of translation of a rolling body (like a ring, disc, cylinder or sphere) at the bottom of an inclined plane of a height h is given by \mathrm{v}^{2}=2 \mathrm{gh} /\left(1+\mathrm{k}^{2} / \mathrm{R}^{2}\right) using dynamical consideration (i.e. by consideration of forces and torques). Note \mathrm{k} is the radius of gyration of the body about its symmetry axis, and \mathbf{R} is the radius of the body. The body starts from rest at the top of the plane.

The given question can be represented as:

where,

R is the body’s radius

g is the acceleration due to gravity

\mathrm{K} is the body’s radius of gyration

v is the body’s translational velocity

\mathrm{m} is the Mass of the body

h is the height of the inclined plane

Total energy at the top of the plane will be potential energy given by,

E_{T} (potential energy) =m g h

Total energy at the bottom of the plane will be given as,

E_{b}=K E_{\text {rot }}+K E_{\text {trans }}

=(1 / 2) \mid \omega^{2}+(1 / 2) \mathrm{mv}^{2}

We know, I=m k^{2} and \omega=v / R

Thus, we have 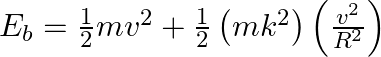E_{b}=\frac{1}{2} m v^{2}+\frac{1}{2}\left(m k^{2}\right)\left(\frac{v^{2}}{R^{2}}\right)

=\frac{1}{2} m v^{2}\left(1+\frac{k^{2}}{R^{2}}\right)

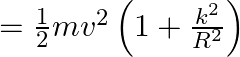
According to the law of conservation of energy, we can write,

E_{T}=E_{b}

m g h=\frac{1}{2} m v^{2}\left(1+\frac{k^{2}}{R^{2}}\right)

\therefore \mathrm{v}^{2}=2 \mathrm{gh} /\left[1+\left(\mathrm{k}^{2} / \mathrm{R}^{2}\right)\right]

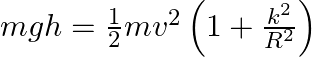
Hence, the given relation is proved.

i

More Material