Here ![]()
(1)
also, ![]()
(2)
Where ![]() and
and ![]() denote the radius vector and velocity of the
denote the radius vector and velocity of the ![]() particle refers to the new origin as the centre of mass
particle refers to the new origin as the centre of mass ![]() ‘, and
‘, and ![]() is the velocity of the centre of mass with respect to
is the velocity of the centre of mass with respect to ![]() .
.
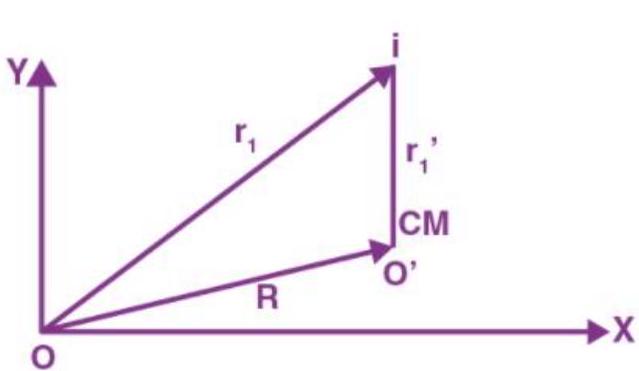
(i) Total angular momentum of the system of particles is calculated below:
![]()
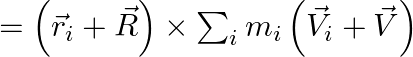
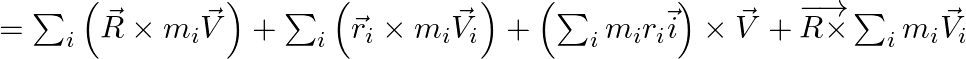
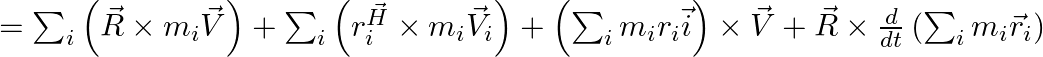
![]()
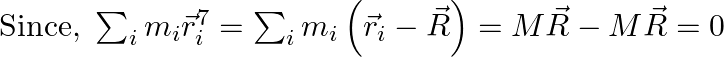
According to the definition of centre of mass, we can write,
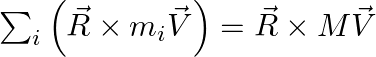
Such that, ![]()
Given, ![]()
Thus, we have ; ![]()
(ii) From previous solution, we have
![]()
![]()
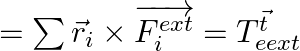
Total torque can be calculated as,
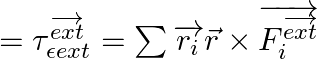
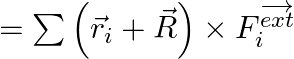
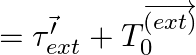
Where, ![]() is the net torque about the centre of mass as origin and
is the net torque about the centre of mass as origin and ![]() is about the origin
is about the origin ![]() .
.
![]()
![]()
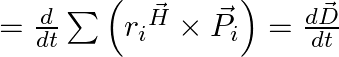
As a result, we have, ![]()
