Show that the function $f: R \rightarrow R: f(x)=x^{4}$ is neither one-one nor onto.

Home » Show that the function is neither one-one nor onto.

Show that the function $f: R \rightarrow R: f(x)=x^{4}$ is neither one-one nor onto.

Solution:

We need to prove: function is neither one-one nor onto
It is given that: $f: R \rightarrow R: f(x)=x^{4}$
We have,
$f(x)=x^{4}$
For, $f\left(x_{1}\right)=f\left(x_{2}\right)$
$\begin{array}{l} \Rightarrow x_{1}^{4}=x_{2}^{4} \\ \Rightarrow\left(x_{1}^{4}-x_{2}^{4}\right)=0 \\ \Rightarrow\left(x_{1}^{2}-x_{2}^{2}\right)\left(x_{1}^{2}+x_{2}^{2}\right)=0 \\ \Rightarrow\left(x_{1}-x_{2}\right)\left(x_{1}+x_{2}\right)\left(x_{1}^{2}+x_{2}^{2}\right)=0 \\ \Rightarrow x_{1}=x_{2} \text { or, } x_{1}=-x_{2} \text { or, } x_{1}^{2}=-x_{2}^{2} \end{array}$
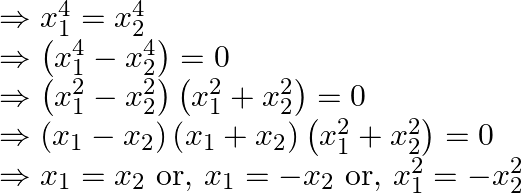
Since we are getting more than one value of $x_{1}$ (no unique image)
$\therefore f(x)$ is not one-one
$f(x)=x^{4}$
Suppose $f(x)=y$ such that $y \in R$
$\begin{array}{l} \Rightarrow y=x^{4} \\ \Rightarrow x=\sqrt[4]{y} \end{array}$
If $y=-2$ , as $y \in R$
Therefore $\mathrm{x}$ will be undefined as we cannot place the negative value under the square root
Therefore $f(x)$ is not onto
As a result, hence proved.