Login/Sign Up
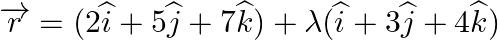
Home » Show that the line line is parallel to the plane . Also, find the distance between them.
Show that the line line \overrightarrow r = (2\widehat i + 5\widehat j + 7\widehat k) + \lambda (\widehat i + 3\widehat j + 4\widehat k) is parallel to the plane \overrightarrow r = (\widehat i + \widehat j - \widehat k) = 7. Also, find the distance between them.
CBSE | Class 12 | Exercise 28G | Maths | RS Aggarwal | The Planes
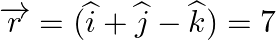
Show that the line line \overrightarrow r = (2\widehat i + 5\widehat j + 7\widehat k) + \lambda (\widehat i + 3\widehat j + 4\widehat k) is parallel to the plane \overrightarrow r = (\widehat i + \widehat j - \widehat k) = 7. Also, find the distance between them.

Answer:

A line 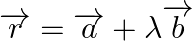\begin{array}{l} \overrightarrow r = \overrightarrow a + \lambda \overrightarrow b \\ \end{array} is parallel to the plane 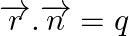\begin{array}{l} \overrightarrow r .\overrightarrow n = q\\ \end{array} only when this line is perpendicular to the normal to the plane.

\begin{array}{l} \overrightarrow b .\overrightarrow n = 0\\ \end{array}

\begin{array}{l} \left( {\overrightarrow b .\overrightarrow n } \right) = (\widehat i + 3\widehat j + 4\widehat k).(\widehat i + \widehat j - \widehat k) = > (1 + 3 - 4) = 0 \end{array}

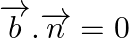
The line is parallel to the given plane.

Required distance between the line and the plane

=|a→·n→–q||n→|=|(2i^+5j^+7k^)·(i^+j^–k^)–7||i^+j¯–k^|=|2+5–7–7|12+12+(–1)2=|–7|3=73 units. 

\begin{array}{l}

=\frac{|\overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{n}}-\mathrm{q}|}{|\overrightarrow{\mathrm{n}}|}=\frac{|(2 \hat{\mathrm{i}}+5 \hat{\mathrm{j}}+7 \hat{\mathrm{k}}) \cdot(\hat{\mathrm{i}}+\hat{\mathrm{j}}-\hat{\mathrm{k}})-7|}{|\hat{\mathrm{i}}+\overline{\mathrm{j}}-\hat{\mathrm{k}}|} \\

=\frac{|2+5-7-7|}{\sqrt{1^{2}+1^{2}+(-1)^{2}}} \\

=\frac{|-7|}{\sqrt{3}}=\frac{7}{\sqrt{3}} \text { units. }

\end{array}

i

More Material