Login/Sign Up
Home » Show that the points P(2, 3, 5), Q(-4, 7, -7), R(-2, 1, -10) and S(4, -3, 2) are the vertices of a rectangle.
Show that the points P(2, 3, 5), Q(-4, 7, -7), R(-2, 1, -10) and S(4, -3, 2) are the vertices of a rectangle.
CBSE | Class 11 | Exercise 26B | Maths | RS Aggarwal | Three Dimensional Geometry
Show that the points P(2, 3, 5), Q(-4, 7, -7), R(-2, 1, -10) and S(4, -3, 2) are the vertices of a rectangle.

Answer:

(x1,y1,z1) = (2, 3, 5)

(x2,y2,z2) = (-4, 7, -7)

(x3,y3,z3) = (-2, 1, -10)

(x4,y4,z4) = (4, -3, 2)

\begin{array}{l} Length PQ = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2} + {{({z_2} - {z_1})}^2}} \\ => \sqrt {{{( -4 - 2)}^2} + {{(7 - 3))}^2} + {{( -7 - 5))}^2}} \\ => \sqrt {36 + 16 + 144} \\ => \sqrt {196} \end{array}

\begin{array}{l} Length QR = \sqrt {{{({x_3} - {x_2})}^2} + {{({y_3} - {y_2})}^2} + {{({z_3} - {z_2})}^2}} \\ => \sqrt {{{( -2 + 4)}^2} + {{(1 - 7))}^2} + {{( -10 + 7))}^2}} \\ => \sqrt {4 + 36 + 9} \\ => \sqrt {19} \end{array}

\begin{array}{l} Length RS = \sqrt {{{({x_4} - {x_3})}^2} + {{({y_4} - {y_3})}^2} + {{({z_4} - {z_3})}^2}} \\ => \sqrt {{{( 4 + 2)}^2} + {{(-3 - 1))}^2} + {{( 2 + 10))}^2}} \\ => \sqrt {36 + 16 + 144} \\ => \sqrt {196} \end{array}

\begin{array}{l} Length PS = \sqrt {{{({x_4} - {x_1})}^2} + {{({y_4} - {y_1})}^2} + {{({z_4} - {z_1})}^2}} \\ => \sqrt {{{( 4 - 2)}^2} + {{(-3 - 3))}^2} + {{( 2 - 5))}^2}} \\ => \sqrt {4 + 36 + 9} \\ => \sqrt {49} \end{array}

\begin{array}{l} Length PR = \sqrt {{{({x_3} - {x_1})}^2} + {{({y_3} - {y_1})}^2} + {{({z_3} - {z_1})}^2}} \\ => \sqrt {{{( -2 - 2)}^2} + {{(1 - 3))}^2} + {{( -10 - 5))}^2}} \\ => \sqrt {16 + 4 + 225} \\ => \sqrt {245} \end{array}

\begin{array}{l} Length QS = \sqrt {{{({x_4} - {x_2})}^2} + {{({y_4} - {y_2})}^2} + {{({z_4} - {z_2})}^2}} \\ => \sqrt {{{( 4 + 4)}^2} + {{(-3 - 7))}^2} + {{( 2 + 7))}^2}} \\ => \sqrt {64 + 100 + 81} \\ => \sqrt {245} \end{array}

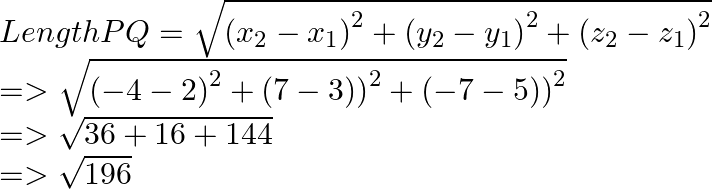
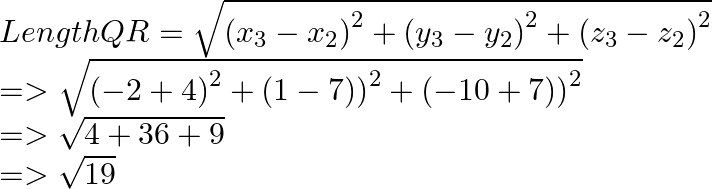
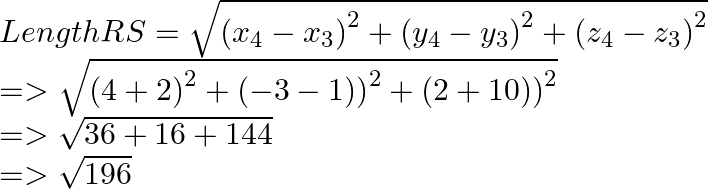
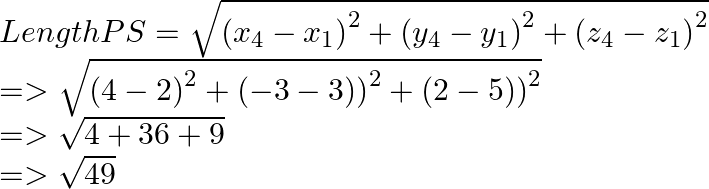
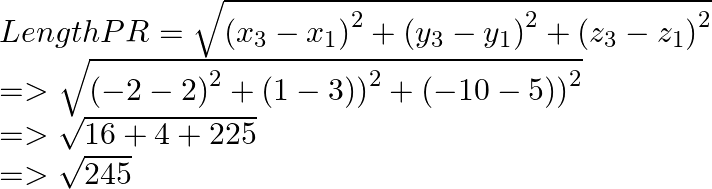
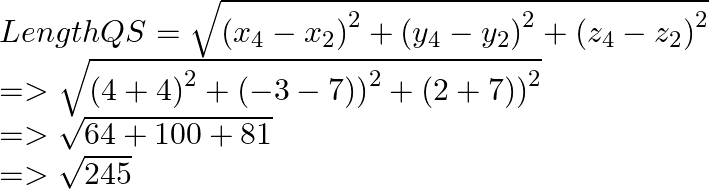
PQ = RS which are opposite sides of polygon.

QR = PS which are opposite sides of polygon.

The diagonals PR = QS.

Hence, the polygon is a rectangle.

i

More Material