Solution:
It is given that:
Volume ![]()
![]()
![]() (constant)
(constant)
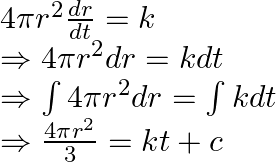
For ![]() and for
and for ![]() , Therefore, we have,
, Therefore, we have,
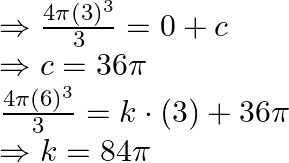
Therefore after ![]() seconds the radius of the balloon will be,
seconds the radius of the balloon will be,
![Rendered by QuickLaTeX.com \begin{array}{l} \Rightarrow \frac{4 \pi r^{3}}{3}=84 \pi t+36 \pi \\ \Rightarrow 4 \pi r^{3}=252 \pi t+108 \pi \\ \Rightarrow r^{3}=\frac{252 \pi t+108 n}{4 \pi} \\ \Rightarrow r^{3}=63 t+27 \\ \Rightarrow r=\sqrt[3]{63 t+27} \end{array}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1f44c82b17958afb4af2576fe20f8c4d_l3.png)
As a result, the radius of the balloon as a function of time is
![]()
Solution:
It is given that:
Volume ![]()
![]()
![]() (constant)
(constant)
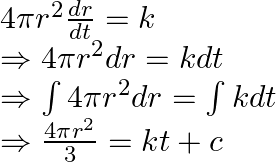
For ![]() and for
and for ![]() , Therefore, we have,
, Therefore, we have,
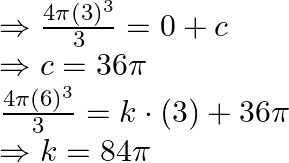
Therefore after ![]() seconds the radius of the balloon will be,
seconds the radius of the balloon will be,
![Rendered by QuickLaTeX.com \begin{array}{l} \Rightarrow \frac{4 \pi r^{3}}{3}=84 \pi t+36 \pi \\ \Rightarrow 4 \pi r^{3}=252 \pi t+108 \pi \\ \Rightarrow r^{3}=\frac{252 \pi t+108 n}{4 \pi} \\ \Rightarrow r^{3}=63 t+27 \\ \Rightarrow r=\sqrt[3]{63 t+27} \end{array}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1f44c82b17958afb4af2576fe20f8c4d_l3.png)
As a result, the radius of the balloon as a function of time is
![]()