Login/Sign Up
Home » The weights of coffee in 70 jars are shown in the following table:     Determine variance and standard deviation of the above distribution.
The weights of coffee in 70 jars are shown in the following table:

    \[\begin{tabular}{|l|l|} \hline Weight (in grams) & Frequency \\ \hline $200-201$ & 13 \\ \hline $201-202$ & 27 \\ \hline $202-203$ & 18 \\ \hline $203-204$ & 10 \\ \hline $204-205$ & 1 \\ \hline $205-206$ & 1 \\ \hline \end{tabular}\]

Determine variance and standard deviation of the above distribution.
CBSE | Class 11 | Maths | NCERT Exemplar | Statistics
The weights of coffee in 70 jars are shown in the following table:

    \[\begin{tabular}{|l|l|} \hline Weight (in grams) & Frequency \\ \hline $200-201$ & 13 \\ \hline $201-202$ & 27 \\ \hline $202-203$ & 18 \\ \hline $203-204$ & 10 \\ \hline $204-205$ & 1 \\ \hline $205-206$ & 1 \\ \hline \end{tabular}\]

Determine variance and standard deviation of the above distribution.

Solution:

The weights of coffee in 70 jars is given

We now need to find the variance and standard deviation of the distribution

Let’s construct a table of the given data and append other columns after calculations

    \[\begin{tabular}{|l|l|l|l|} \hline Weight (in grams) & Mid-Value $\left(\mathrm{x}_{\mathrm{i}}\right)$ & Frequency $\left(\mathrm{f}_{\mathrm{i}}\right)$ & $\mathrm{f}_{\mathrm{i}} x_{i}$ \\ \hline $200-201$ & $200.5$ & 13 & $13 \times 200.5=2606.5$ \\ \hline $201-202$ & $201.5$ & 27 & $27 \times 201.5=5440.5$ \\ \hline $202-203$ & $202.5$ & 18 & $18 \times 202.5=3645$ \\ \hline $203-204$ & $203.5$ & 10 & $10 \times 203.5=2035$ \\ \hline $204-205$ & $204.5$ & 1 & $1 \times 204.5=204.5$ \\ \hline $205-206$ & $205.5$ & 1 & $1 \times 205.5=205.5$ \\ \hline & Total & $\mathrm{N}=70$ & $\sum \mathrm{f}_{\mathrm{i}} x_{i}=14137$ \\ \hline \\ \end{tabular}\]

Mean, \overline{\mathrm{x}}=\frac{\sum f_{\mathrm{i}} \mathrm{X}_{\mathrm{i}}}{\mathrm{N}}=\frac{14137}{70}=201.9

Therefore the above table with more columns is shown below,

\begin{tabular}{|l|l|l|l|l|l|}
\hline Weight (in grams) & MidValue \left(\mathrm{x}_{i}\right) & Frequency \left(f_{i}\right) & d_{i} =x_{i}-\bar{x} & \mathrm{fi}_{i} \mathrm{~d}_{i} & \mathrm{fi} \mathrm{d}_{i}{ }^{2} \\
\hline 200-201 & 200.5 & 13 & 200.5- 201.9= -1.4 & 13 x-1.4= -18.2 & 13 \times-1.4^{2} =25.48 \\
\hline 201-202 & 201.5 & 27 & 201.5- 201.9= -0.4 & 27 \times-0.4= -10.8 & 27 \times-0.4^{2} =4.32 \\
\hline 202-203 & 202.5 & 18 & 202.5- 201.9= 0.6 & 18 \times 0.6= 10.8 & 18 \times 0.6^{2}= 6.48 \\
\hline 203-204 & 203.5 & 10 & 203.5- 201.9= 1.6 & 10 \times 1.6= 16 & 10 \times 1.6^{2}= 25.6 \\
\hline 204-205 & 204.5 & 1 & 204.5- 201.9= 2.6 & 1 \times 2.6= 2.6 & 1 \times 2.6^{2} =6.76 \\
\hline 205-206 & 205.5 & 1 & 205.5- 201.9= 3.6 & 1 \times 3.6= 3.6 & 1 \times 3.6^{2} =12.96 \\
\hline & Total & N=70 & & \Sigma f_{i} d_{i}=4 & \Sigma f_{i} d_{i}^{2} =81.6 \\
\hline
\end{tabular}

And the standard deviation is

\sigma=\sqrt{\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{d}_{\mathrm{i}}^{2}}{\mathrm{n}}-\left(\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{d}_{\mathrm{i}}}{\mathrm{n}}\right)^{2}}

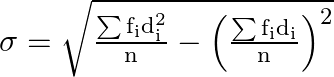
Substitute the values from above table,

\begin{aligned} &\sigma=\sqrt{1.17-(0.057)^{2}} \\ &\sigma=\sqrt{1.17-0.003249}=\sqrt{1.17} \\ &\Rightarrow \sigma=1.08 \mathrm{~g} \\ &\text { And } \sigma^{2}=1.08^{2}=1.17 \mathrm{~g} \end{aligned}

\sigma=\sqrt{\frac{81.6}{70}-\left(\frac{4}{70}\right)^{2}}

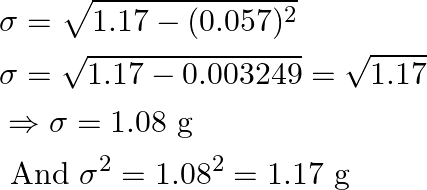
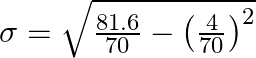
As a result, the variance and standard deviation of the distribution are respectively 1.166 \mathrm{~g} and 1.08.

i

More Material