Login/Sign Up
Home » Without expanding the determinant, prove that . SINGULAR MATRIX A square matrix is said to be singular if . Also, is called non singular if .
Without expanding the determinant, prove that \left|\begin{array}{ccc}41 & 1 & 5 \\ 79 & 7 & 9 \\ 29 & 5 & 3\end{array}\right|=0. SINGULAR MATRIX A square matrix A is said to be singular if |A|=0. Also, A is called non singular if |A| \neq 0.
CBSE | Class 12 | Determinants | Exercise 6A | Maths | RS Aggarwal
Without expanding the determinant, prove that \left|\begin{array}{ccc}41 & 1 & 5 \\ 79 & 7 & 9 \\ 29 & 5 & 3\end{array}\right|=0. SINGULAR MATRIX A square matrix A is said to be singular if |A|=0. Also, A is called non singular if |A| \neq 0.

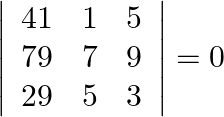
Solution:

We know that C_{1} \Rightarrow C_{1}-C_{2}, would not change anything for the determinant.
Applying the same in above determinant, we get
\left[\begin{array}{lll}40 & 1 & 5 \\ 72 & 7 & 9 \\ 24 & 5 & 3\end{array}\right] Now it can clearly be seen that C_{1}=8 \times C_{3}
Applying above equation we get,
\left[\begin{array}{lll} 0 & 1 & 5 \\ 0 & 7 & 9 \\ 0 & 3 & 3 \end{array}\right]
We know that if a row or column of a determinant is 0 . Then it is singular determinant.

i

More Material