
كونك أحد الطلاب الذين يستعدون لاختبار القدرات العامة فبلا شك ستبحث عن أسئلة لا يخلو منها اختبار القدرات كي تتدرب على حلها جيداً، فمن اسمها لا يخلو منها أي اختبار أي أنه إذا لم تأتي كما هي سيأتي مثلها على نفس النمط.
اختبار القدرات العامة من اسمه يعمل على قياس قدرات الطالب لذلك فإنه ليس ضد الطالب كما يعتقد البعض ولا يركز فقط على الأسئلة الصعبة, بل ينوع في هذه الأسئلة كي يتم قياس مختلف المهارات المطلوبة في هذا الاختبار والتي تساعد الطالب في اكتشاف قدراته ومن ثم تحديد أكثر التخصصات ملاءمة له في الجامعة.
في هذا المقال أحضرنا لكم مجموعة أسئلة لا يخلو منها اختبار القدرات وهي تتعلق بالقسم الكمي في الاختبار, ومن المعروف بأن هذا النمط يتكرر في كل عام وخصوصًا الأسئلة التي تتعلق بالكسور والأسس والعمليات الهامة التي تتعلق بها, فتابعوا معنا هذه الأسئلة وتدربوا على الحل بيدكم وليس فقط الاطلاع على الأسئلة بأعينكم فهذا لا يفيد في التدرب على المسائل الحسابية.
أسئلة لا يخلو منها اختبار القدرات
فيما يلي إليكم مجموعة أسئلة لا يخلو منها اختبار القدرات, مع التنويه أنها أُخذت من قناة نون أكاديمي الغنية عن التعريف والتي إذا قمتم بزيارتها على اليوتيوب ستجدون المزيد من هذه الأسئلة هنا. أما الآن فإليكم مقتطفات فقط من الأسئلة الهامة:
السؤال الأول:
السؤال الأول من أسئلة لا يخلو منها اختبار القدرات
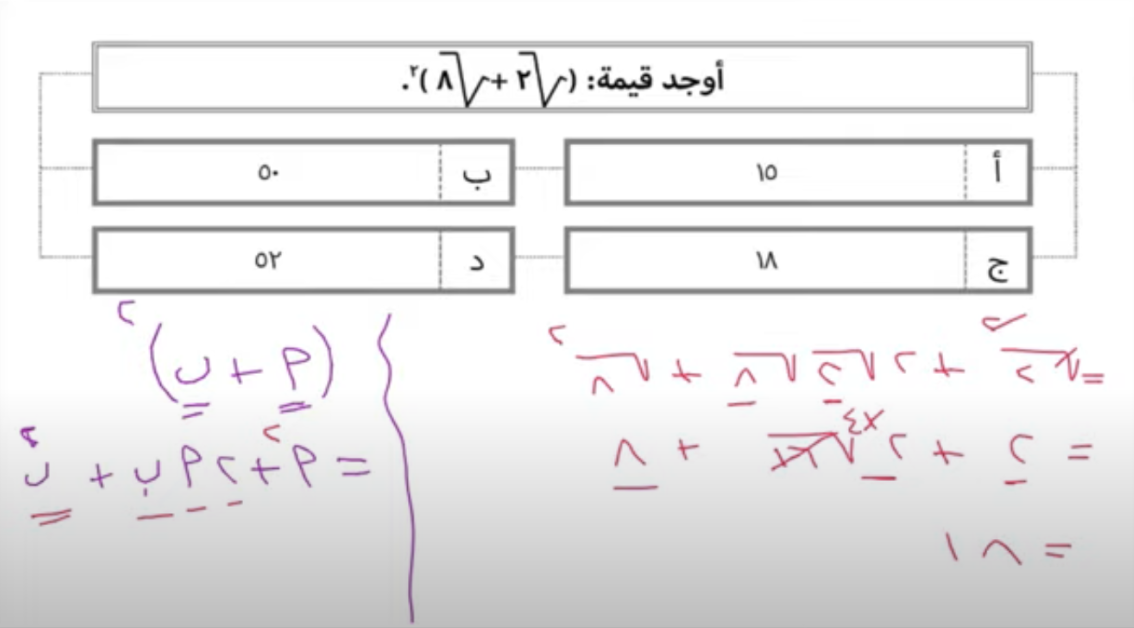
كما ترون الحل واضح في الصورة, حيث أننا لدينا جذور مربعة والتي يتم حلها عبر قانون مجموع مربعين الموضح أعلاه. ويتم التعويض باستخدام المعطيات وننوه أنه عند وجود تربيع أعلى الجذر فإننا نتخلص من الجذر والتربيع مع بعضهما البعض أي أنهما يلغيان وجود بعض. والإجابة الصحيحة بعد جمع الحدود هي 18.
السؤال الثاني:
السؤال الثاني من أسئلة لا يخلو منها اختبار القدرات 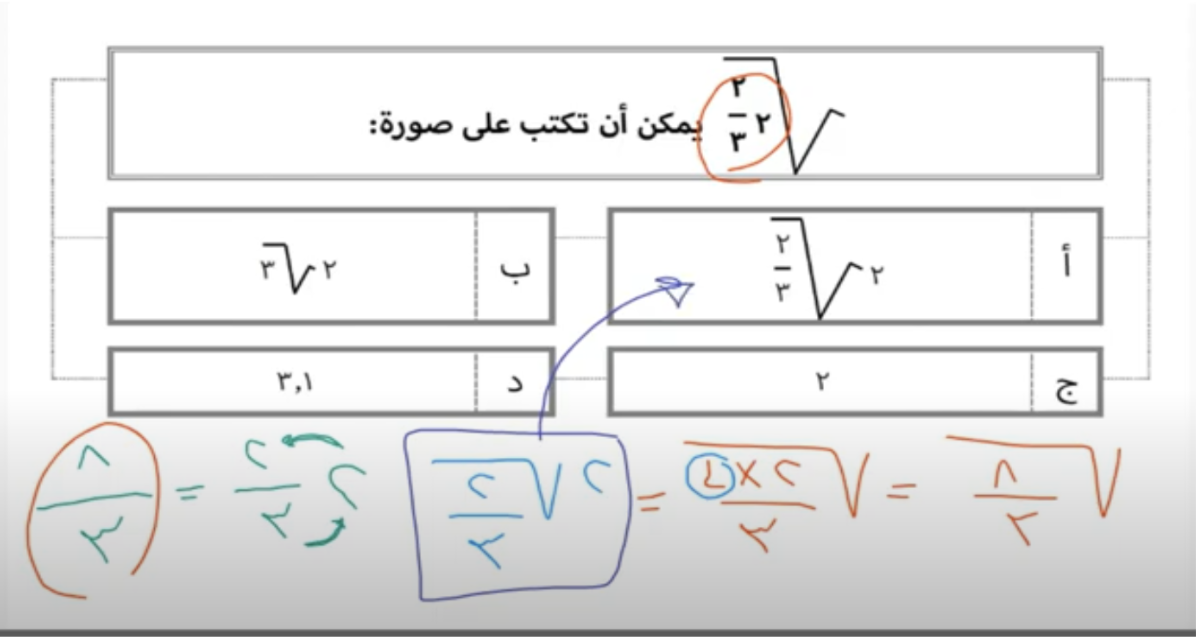
في البداية لحل السؤال كما تلاحظون قمنا بالتحويل إلى كسر عادي من خلال ابقاء المقام 3 كما هو ومن ثم ضرب 2*3 وجمعهما مع البسط 2 فيكون الناتج 8 في البسط والمقام 3. ومن ثم سيصبح لدينا جذر 8/3 ولتبسيطه نقوم بأن 8 عبارة عن 2*4 ويبقى المقام 3 كما هو, بعد ذلك نسأل أنفسنا أي من الأعداد في البسط يمكن أن يتم تبسيطها فنجد بأن 4 عبارة عن 2*2, لذلك نخرج 2 قبل الجذر ونبقي واحدة في الداخل وبذلك نصل إلى الجواب النهائي وهو 2 جذر 2/3.
السؤال الثالث:
السؤال الثالث من أسئلة لا يخلو منها اختبار القدرات

للحل سنقوم بتحليل الجذور في البداية فنحلل 18 إلى 2*9, ونحلل 8 إلى 2*4, بعد ذلك بما أن جذر 9 هو 3 سنضرب 3 في 4 ويكون الناتج 12 جذر 2. في الجذر الأخر نقول بأن جذر 4 هو 2 فنخرجها إلى الخارج تصبح 2 جذر 2, ويبقى المقام كما هو. بما أن جذر 2 مكرر في الحدين يمكننا الطرح بشكل عادي 12-2 ويساوي 10 جذر 2, والمقام كما هو 5 جذر 2. بما أن جذر 2 مكرر في الأعلى والأسفل فإننا نتخلص منه ويبقى لدينا 10/5 وتساوي 2 وهو الإجابة الصحيحة.
السؤال الرابع:
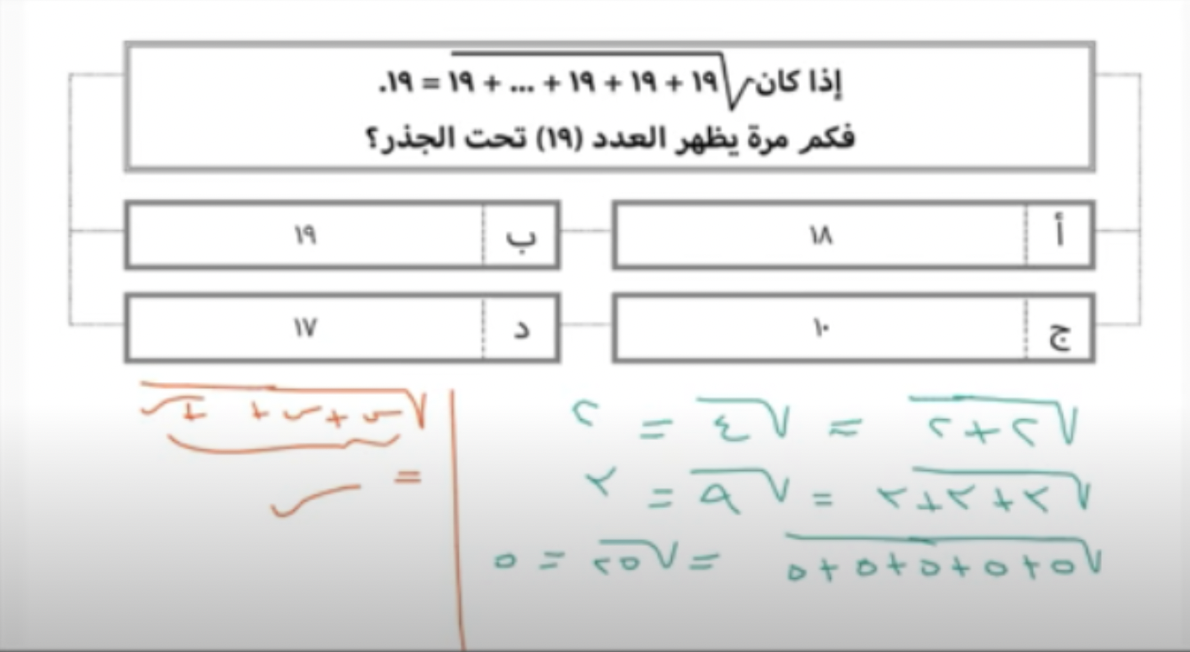 السؤال الرابع من أسئلة لا يخلو منها اختبار القدرات
السؤال الرابع من أسئلة لا يخلو منها اختبار القدرات
ويعتبر هذا من ضمن أسئلة لا يخلو منها اختبار القدرات , ولحله ننظر إلى الثلاث أمثلة على اليمين والتي من خلالها تم استنتاج المبدأ على اليسار وهو أن جذر مجموع س + س +س…دائماً تكون إجابته س من المرات. وبذلك نستنتج أن الإجابة الصحيحة هي 19.
السؤال الخامس:
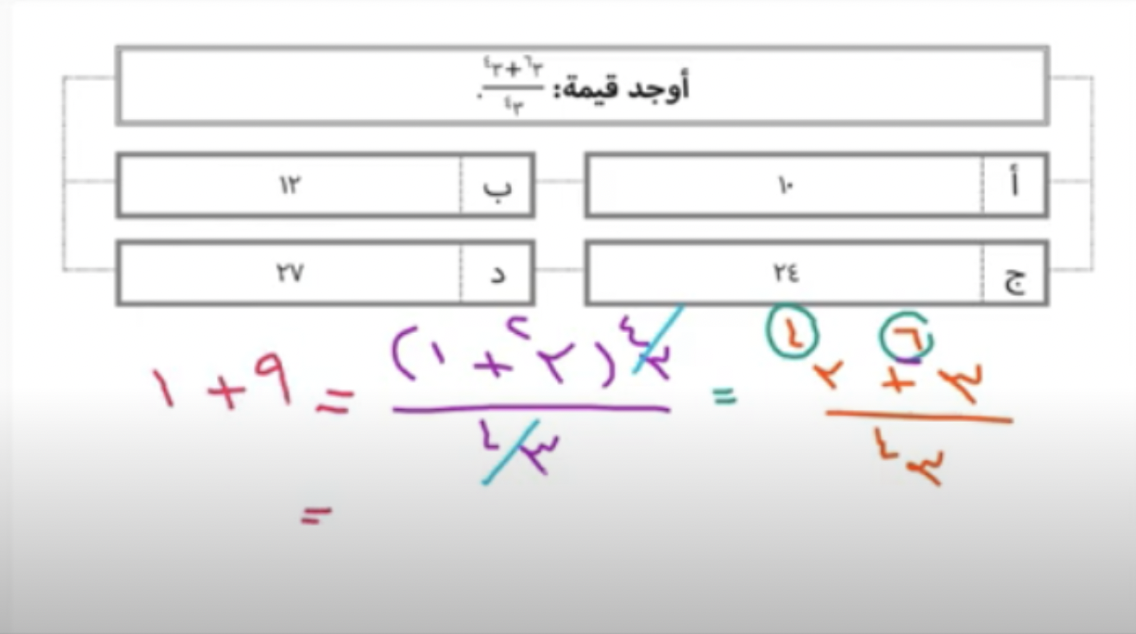
السؤال الخامس من أسئلة لا يخلو منها اختبار القدرات
إن فكرة السؤال الأساسية مبنية على إيجاد العامل المشترك بين الأسس في البسط, فكما نرى عند تبسيط البسط يكون 2 هو العامل المشترك بين الأسس. ثم نقوم باختصار 3 أس 4 في البسط مع المقام. يتبقى لنا 3 أس 2 وهي عبارة عن 9 وأخيراً نجمع 9+1 ويكون الناتج هو 10 أي أن الإجابة الصحيحة هي الخيار أ.
السؤال السادس:
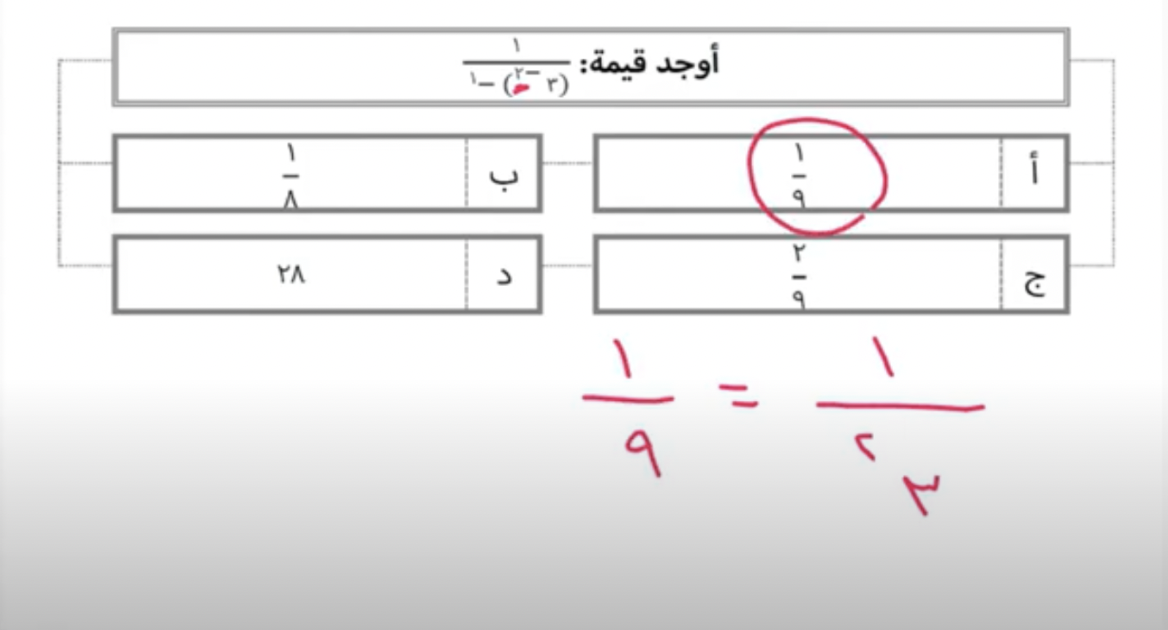 السؤال السادس من أسئلة لا يخلو منها اختبار القدرات
السؤال السادس من أسئلة لا يخلو منها اختبار القدرات
طريقة الحل السريعة في هذا السؤال كانت ضرب القوى أي ضرب الأسس في المقام فقمنا بضرب الأس -2 * الأس -1 فيكون ناتج الأسس هو +2, ويصبح لدينا الكسر عبارة عن 1/ 3 أس 2, والذي يعني 1/9 وهو الخيار الصحيح أ.
السؤال السابع:
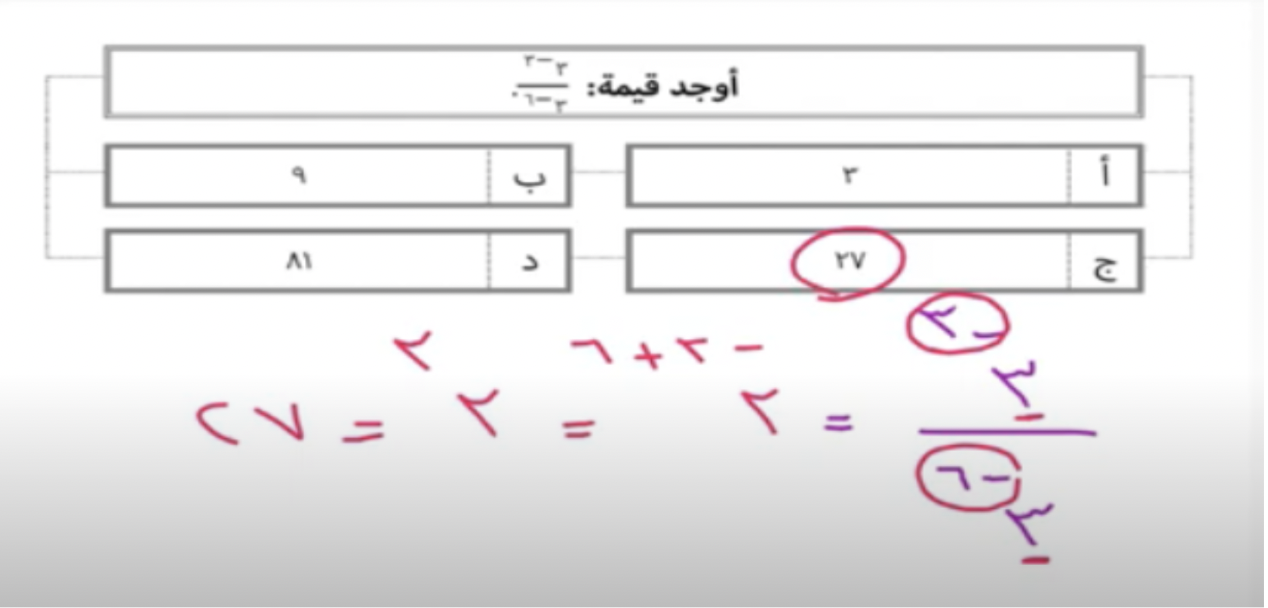
السؤال السابع من أسئلة لا يخلو منها اختبار القدرات
وفي هذا السؤال من ضمن أسئلة لا يخلو منها اختبار القدرات, بما أن لدينا قسمة كسور, فإن المبدأ الذي نتبعه هو طرح الأسس , أي نطرح الأس -3- -6, ويصبح
– 3+6 =3, وبالتالي 3 أس 3 تساوي 27 وهي الإجابة الصحيحة.
ختامًا ..
وبهذا ننهي مقالنا لهذا اليوم والذي ذكرنا فيه مجموعة أسئلة لا يخلو منها اختبار القدرات الكمي وذلك لتسهيل دراسة ومذاكرة القسم الكمي للطلاب, حيث أنه يسبب خوف وقلق كبير لدى نسبة كبيرة من الطلاب وخصوصاً من لم يأخذوا وقت كافي في التأسيس, ويبحثون عن أساسيات في الاختبار وتتكرر في كل مرة لمذاكرتها جيداً وضمان اجتياز الأسئلة المشابهة لها في الاختبار.


