If you are new to programming or simply want to understand how the hexadecimal number system works, then this blog is for you! Hexadecimal numbers are represented by a string of letters and numbers that has 16 different characters. For example, the hexadecimal number “FFFF” is often shown as “255” because each hexadecimal character represents four binary digits. Read on for more information on the hexadecimal number system.
What is the hexadecimal number system?
The hexadecimal number system is a base-16 number system that uses the digits 0-9 and the letters A-F to represent numbers. The hexadecimal number system has 16 possible values for each digit, which allows for a larger range of numbers to be represented than in the decimal number system.
The hexadecimal number system is commonly used in computer science because it provides an easy way to represent binary data. When converting from binary to hexadecimal, each group of four bits is represented by a single hexadecimal digit. For example, the binary number 1010 can be represented as the hexadecimal number A. This makes it easy to convert between the two systems when working with computer code.
The hexadecimal number system can also be used to represent colors on a computer screen. Each color is represented by a six-digit hexadecimal code, which includes a mix of the digits 0-9 and the letters A-F. For example, the color black can be represented as #000000, while the color white can be represented as #FFFFFF.
How the hexadecimal number system works
The hexadecimal number system is a base 16 number system. This means that there are 16 possible digits that can be used to represent a number. The most common digits used are 0-9 and A-F.
To understand how the hexadecimal number system works, it is first important to understand how the decimal number system works. In the decimal number system, there are 10 possible digits that can be used to represent a number (0-9). Each digit in a decimal number has a place value. The place value of a digit is determined by its position in the number. For example, in the number 123, the 1 has a place value of 100, the 2 has a place value of 10, and the 3 has a place value of 1.
The hexadecimal number system works similarly to the decimal number system, except there are 16 possible digits that can be used instead of 10. As with the decimal system, each digit in a hexadecimal number has a place value. However, since there are more digits in the hexadecimal system, the place values are different. In the hexa decimal number system, the place values of digits increase by powersof16 as you move from right to left instead of powers of 10 like in decimal system. For example, in thenumber1234hthe1hasaplacevalueof16^3=4096 ,the2hasaplacevalue
The benefits of the hexadecimal number system
The hexadecimal number system is a base 16 number system that uses the digits 0-9 and the letters A-F to represent numbers. This number system is used in many applications, such as computer programming, because it is easy to convert between binary (the language computers use) and hexadecimal.
The main benefit of the hexadecimal number system is its simplicity. Because there are only 16 symbols used to represent numbers, it is easy to convert between different bases (such as binary and decimal). Hexadecimal is also more compact than other number systems, which makes it ideal for storage and transmission.
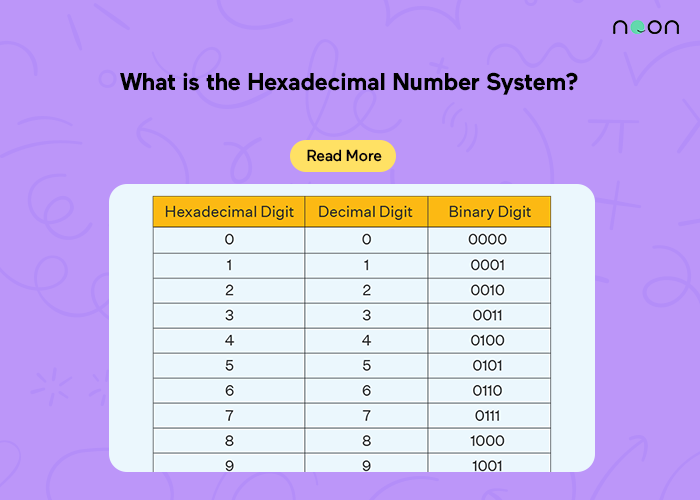
Hexadecimal conversion table
The hexadecimal number system is a base 16 number system. This means that there are 16 digits in the system, 0-9 and A-F. The hexadecimal conversion table below shows the decimal values for each of the hexadecimal digits:
Hexadecimal Conversion Table
Digit Decimal Value
0 0
1 1
2 2
3 3
4 4
5 5
6 6
7 7
8 8
9 9
A 10
B 11
C 12
D 13
E 14
How to convert Hexadecimal to Binary?
The Hexadecimal number system is a base 16 number system that uses the letters A-F to represent the 10-15 values. To convert a Hexadecimal number to Binary, simply write out the hexadecimal number as if it were a normal base 10 number, and then break it into groups of 4 binary digits.
For example, the hexadecimal number “AF” would be written out as “10” in base 10, which can then be broken into two groups of 4 binary digits: “1000” and “1111”. Therefore, the binary equivalent of “AF” is “10001111”.
Conclusion
The hexadecimal number system is a great alternative to the more traditional decimal system. It is especially useful for representing numbers in computer code. If you are working with large numbers, the hexadecimal system can be a handy way to keep track of them.
If you’re looking to learn about other subjects, there’s no better place to start than with the Noon app. With over 10,000 lectures available, you can learn at your own pace and from anywhere in the world. Plus, with teachers from all over the globe, you’re sure to find the perfect educator for your needs. So what are you waiting for? Download the Noon app now and start learning today!


