
If you’re new to real and complex numbers, you might be wondering what they are, and why you should care. In this post, we’ll give you a quick overview of what real and complex numbers are, and then show you a few examples that will help you understand them better. So read on, and let us teach you all about complex numbers!
What are Real numbers?
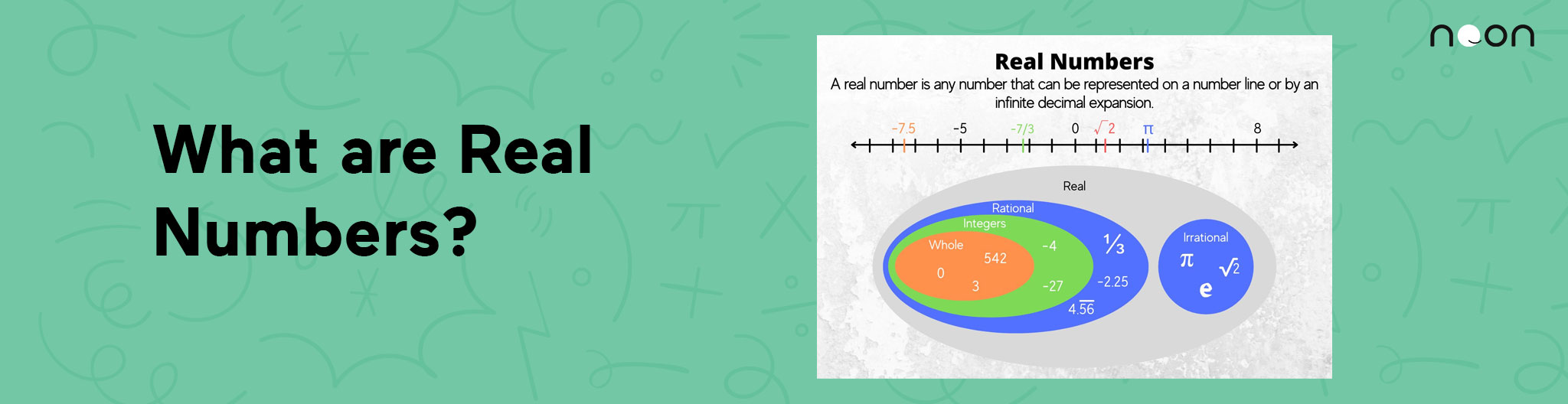
Real numbers are the basic building blocks of mathematical reality. They exist outside of any physical dimension and can be represented by a unique set of numerical symbols.
Every real number has a corresponding positive or negative counterpart, and they can be ordered along any named axis (such as magnitude, time, etc.). Real numbers also have many properties that make them particularly useful in mathematics and science. For example, they obey laws such as the Pythagorean theorem and the law of quadratic reciprocity.
Real Numbers Example
Here are the examples of real numbers
- Integers are whole numbers that can be expressed as a combination of 1, 2, 3…n digits. For example, integers are (-4,0,4)
- Fractions are mathematical quantities that represent part of a whole by dividing it into smaller parts. Fractions can also be expressed in terms of decimals (e.g., 0.5 represents half).
- Irrational numbers are real numbers that cannot be expressed as fractions or integers (for example, π2).
Complex Numbers Definition

A complex number is a mathematical object that consists of a real part (a number representing the physical reality) and an imaginary part (a number that represents the mathematical concept of an unreal quantity). Together, these two parts define its magnitude.
Complex numbers can be used in many different ways, including solving equations and problems in physics and engineering. They also play an important role in mathematics, statistics, signal processing, and other fields.
Complex Numbers Example
Complex numbers can be tough to understand at first, but once you have a basic understanding they can be very helpful in solving problems. Here are some examples:
- The equation y = x + i has the solution y = –x + i. This is because the imaginary part of the equation accounts for the fact that when we add two real numbers together their squares will always equal 1. The complex number (-1+i) represents this answer nicely.
- If you want to find out how long it will take for something to reach its maximum speed, you need to use calculus. One approach would be to use exponential functions and simplify them until you get rid of all negative terms; this would give you y = ct where c is an arbitrary constant (in this case, 2). Now plug in t into both sides of the equation: y = ct2 -> You’ve solved for y using Complex Numbers!
Complex numbers play an important role in many mathematical situations – so learning about them isn’t a waste after all!
Conclusion
By now you might have understood the difference between real numbers and complex numbers. Using this knowledge, you can now answer any question related to these two kinds of numbers, but if it’s still confusing, feel free to leave a comment below!


