Real numbers are the foundation of mathematics and physics, and they are essential for understanding how the world works. They provide a way to compare different quantities, and they can be used to solve equations and problems. In this article, we will discuss what real numbers are, why they are important, and their properties. We will also provide tips on how to use real numbers in your everyday life. Ready to learn more? Let’s start!
What are Real Numbers?
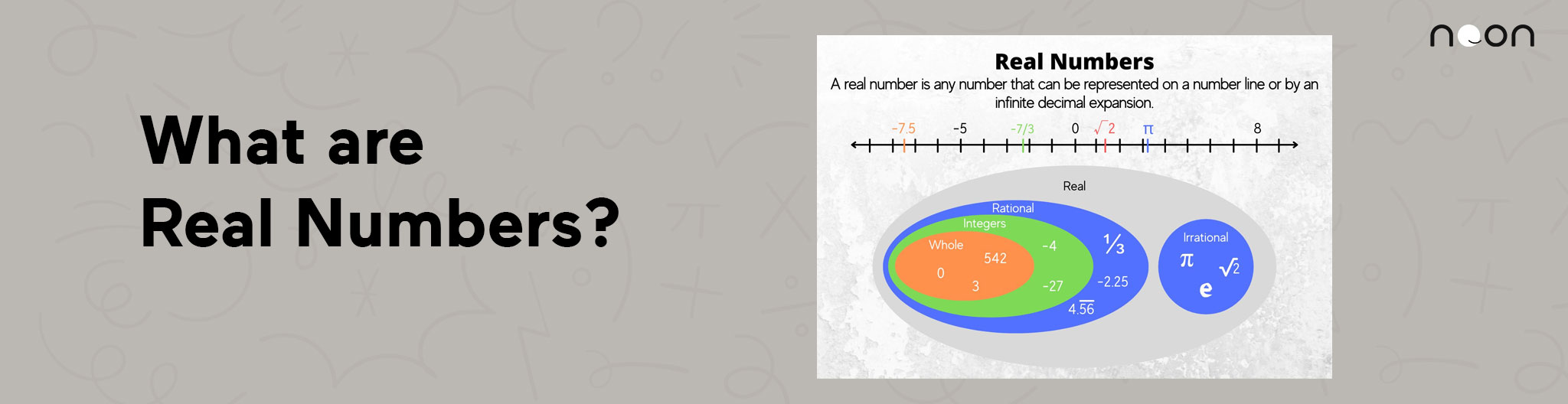
Real numbers are a fundamental concept in mathematics. They allow for precise and accurate calculations, as well as reliable measurements. Real numbers exist independently of any particular scale or measure, which makes them perfect for scientific and mathematical applications.
To understand real numbers better, let’s take a look at an example: 9 + 4 = 15. This simple equation can be represented using real number notation (which we’ll use throughout this article). The first number (9) is written on the left side of the equals sign (=), while the second number (4) is written on the right side of the equal sign. Together, these two numbers represent what’s called a rational expression – something that can be expressed as a quotient and an integer together (like 9/5). In other words, 9 + 4 equals 15 because it represents both halves of a rational expression: 5+1= 6 and 2+1= 3.
here’s no need to worry about fractions here; everything will work just fine with whole-number ratios like this one.
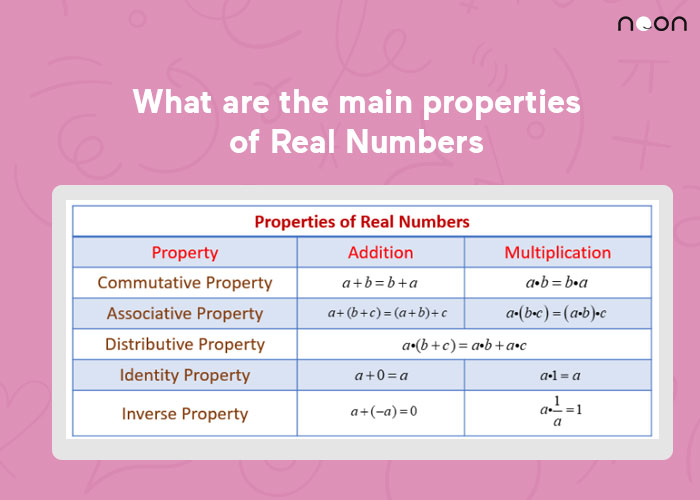
Properties of Real Numbers

Real numbers are the foundation of mathematics and physics. They provide a way to represent physical quantities, such as distances and time, in a systematic way. Real numbers also allow for comparisons between different physical systems. Here are 3 properties of real numbers
Commutative Property
Commutative properties state that the order in which two real numbers are added or multiplied does not affect their sum or product. This is called the Commutative Property of Addition and Multiplication. For example, 4 + 3 = 5 because the order of addition doesn’t matter. Similarly, 6 * 2 = 12 because the order of multiplication doesn’t matter.
Associative Property
Associative properties state that regrouping numbers that are added or multiplied does not affect their sum or product. For example, 4 + (3 + 2) = 9 because 4 gets combined with 3 and 2 to make 9 once again (4+3+2=9).
Distributive Property
The property of real numbers distributive property states that multiplication distributes over addition or difference between two or more terms. In other words, the order in which the terms are multiplied doesn’t affect the result. For example, 3x + 4y = 10 does not change even if you perform the additions first (3+4) and then y (5) because 5 is included in both equations and has been distributed to each term equally.
Identity Property
Whenever you multiply a number by 1, it results in itself. For example, 5 × 1 = 5. And likewise, when you add 0 to a number, it equals itself: 4 + 0 always equals 3. This is called the property of real numbers – adding or multiplying zero doesn’t change the value of the number.
Conclusion
Well, there you have it! These are just some of the properties of real numbers. Try them out and see if you can make any new discoveries. If not, check back later when you get the chance to see how they all work together in a school experiment!
Thank you for downloading the Noon app! Our app has over 10,000 lectures on different subjects, so you can learn from the best teachers from across the globe. You can also find helpful tips and advice to help you ace your next exam. We hope that our app helps you as much as it has helped us. Thank you again!


