Understanding the concept of Gaussian is important for many applications in mathematics, physics, and engineering. In this blog post, we will discuss what the Gaussian surface is, its applications, and how to calculate it. We’ll also provide examples of how Gaussian surfaces can be used to solve real-world problems.
What is Gaussian Surface?
A Gaussian surface, also known as a closed surface, is a three-dimensional closed surface that encloses a volume. It is the three-dimensional analog of a two-dimensional closed curve. In other words, it is a surface that bounds a finite region in space. The name “Gaussian surface” comes from the fact that it was first studied by Carl Friedrich Gauss.
A Gaussian surface can be thought of as the boundary of a three-dimensional object. To visualize this, imagine a sphere. The surface of the sphere is the Gaussian surface enclosing the volume inside the sphere. The sphere itself is the three-dimensional object whose boundary is the Gaussian surface.
Gaussian surfaces are important in physics because they allow for the application of Gauss’s law, which is a powerful tool for understanding electric and magnetic fields.
The Different Types of Gaussian Surfaces
There are three main types of Gaussian surfaces: the sphere, the cylinder, and the plane. Each type has its own unique properties and applications.
The sphere is the simplest and most common type of Gaussian surface. It is defined by a single point in space, called the center, and a radius. The sphere is symmetrical in all directions around the center, which makes it ideal for applications such as measuring the strength of an electric field or calculating the volume of a liquid.
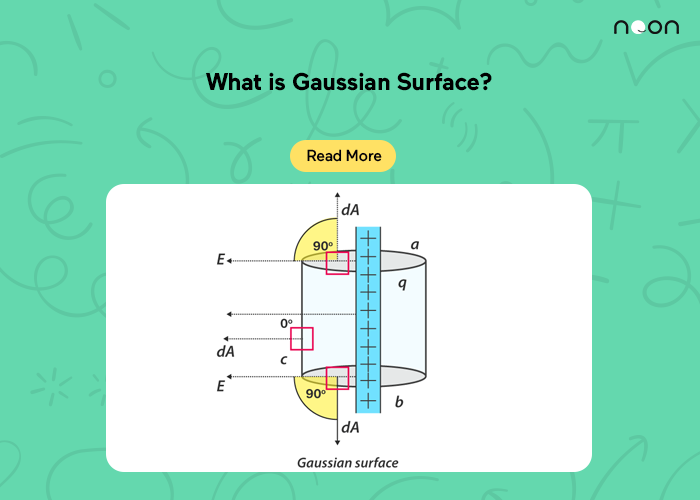
The cylinder is another common type of Gaussian surface. It is defined by two parallel planes and a radius. The cylinder is useful for applications such as measuring the flow rate of a fluid or determining the resistance of a material to electric current.
The plane is the third type of Gaussian surface. It is defined by two points in space, called the edges. The plane is useful for applications such as measuring the area of a surface or calculating the properties of a two-dimensional object.
Pros and Cons of Gaussian Surface
When it comes to the Gaussian surface, there are both pros and cons that need to be considered. For starters, let’s take a look at the pros. One major advantage of the Gaussian surface is that it can be used to calculate the electric field. This is done by using the charge enclosed within the Gaussian surface. Additionally, the Gaussian surface can be used to calculate the magnetic field. This is done by using the current enclosed within the Gaussian surface. Another pro of the Gaussian surface is that it is relatively easy to visualize. When trying to visualize something like an electric field, the Gaussian surface makes things much simpler.
Now let’s take a look at some of the cons of Gaussian surface. One downside is that it can be difficult to apply in certain situations. For example, when there are multiple charges or when the charges are not evenly distributed, the Gaussian surface can become complicated quickly. Additionally, the Gaussian surface relies on certain assumptions that may not always hold true in real-world scenarios. For instance, it assumes that there are no sources or sinks of charge within the enclosed volume. Finally, the Gaussian surface only considers static fields. This means that it cannot be used to calculate fields that are changing over time (such as electromagnetic fields).
Overall, there are both pros and cons to using the Gaussian surface. It is a powerful tool that can be useful in many scenarios but it also has its limitations. When deciding whether or
What are the Uses of Gaussian Surface?
A gaussian surface is a tool used in electrostatics to determine the electric field at a given point. It is also used in magnetostatics to determine the magnetic field at a given point.
How to Make a Gaussian Surface?
A Gaussian surface is a closed surface that encloses a volume of space and whose outward normal field is everywhere perpendicular to the inward-pointing gradient of the enclosed volume’s scalar field. In other words, it is a three-dimensional surface that divides a four-dimensional space into two distinct regions, with one region containing all the points whose scalar value is greater than that of the other region.
There are many ways to create a Gaussian surface, but the most common method is to use a computer program. Once you have chosen the program you want to use, you will need to select the type of surface you want to create. For this example, we will use a sphere.
After selecting the type of surface, you will need to enter the values for the radius and center of the sphere. These values can be found in any standard mathematical textbook. Once you have entered these values, you will need to click on the “generate” button. This will generate a three-dimensional image of your Gaussian surface.
Conclusion
Gaussian surfaces are a powerful tool used to help visualize and understand electrostatic fields in three dimensions. They can also be used to calculate electric flux, which is useful information for many different applications. Gaussian surfaces are just one of many ways that scientists can utilize mathematics and physics to study the behavior of electricity. With further research, this knowledge could lead us to even greater insights into the way our world works on an atomic level.
Noon is an application that allows you to learn from the best teachers from across the globe. With over 10,000 lectures on different subjects, Noon is the ultimate teacher’s assistant tool for e-learning. The app provides teachers with tools for online teaching, including video streams, high-quality videos, and interactive classrooms.


