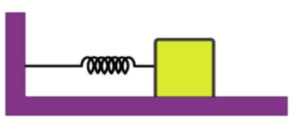
Determine<br>(i) the frequency of oscillations,
(ii) maximum acceleration of the mass
Solution:
Spring constant is given as ![]()
Mass is given as ![]()
Displacement is given as ![]()
![]()
(i) Frequency of oscillation ‘ ![]() ‘ can be calculated as,
‘ can be calculated as,
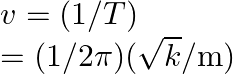
Where,
![]() time period
time period
So,
![]()
![]()
As a result, the frequency of oscillations is ![]() cycles per second.
cycles per second.
(ii) Maximum acceleration (a) is given by the relation:
![]()
Where,
![]()
![]() Maximum displacement
Maximum displacement
So,
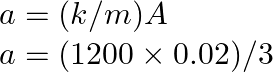
![]()
As a result, the maximum acceleration of the mass is ![]()
