a) Current is given as I = V/R from the Ohm’s law Therefore, I = 1A But, I = ne Avd vd = I/neA When the values for the above parameters are substituted, vd = 1/1.6 × 10-4 m/s The KE = (KE of one...
In an experiment with a potentiometer, VB = 10V. R is adjusted to be 50 Ω. A student wanting to measure voltage E1 of a battery finds no null point possible. He then diminishes R to 10 Ω and is able to locate the null point on the last segment of the potentiometer. Find the resistance of the potentiometer wire and potential drop per unit length across the wire in the second case.
Equivalent resistance of the potentiometer = 50 Ohm + R’ Equivalent voltage across the potentiometer = 10 V Current through the main circuit I = 10/(50 Ohms +R’) Potential difference across wire of...
A room has AC run for 5 hours a day at a voltage of 220V. The wiring of the room consists of Cu of 1 mm radius and a length of 10 m. Power consumption per day is 10 commercial units. What fraction of it goes in the joule heating in wires? What would happen if the wiring is made of aluminium of the same dimensions?
Power consumption in a day = 10 units Power consumption per hour = 2 units Power consumption = 2 units = 2 kW = 2000 J/s Power consumption in resistors, P = VI Which gives I = 9A We know that...
Two cells of voltage 10V and 2V and internal resistances 10Ω and 5Ω respectively are connected in parallel with the positive end of the 10V battery connected to the negative pole of 2V battery. Find the effective voltage and effective resistance of the combination.
Kirchhoff’s law is applied at c, I1 = I + I2 Kirchhoff’s law is applied at efbae, 10 – IR – 10I2 = 0 10 = IR + 10I1 Kirchhoff’s law is applied at cbadc, -2-IR+5I2 = 0 2 = 5I2- RI I2 = I1 – I...
Suppose there is a circuit consisting of only resistances and batteries and we have to double all voltages and all resistances. Show that currents are unaltered.
Reff is the equivalent internal resistance of the battery Veff is the equivalent voltage of the battery Using Ohm’s law, I = Veff/(Reff + R) When the resistance and effective voltage are increased...
Two conductors are made of the same material and have the same length. Conductor A is a solid wire of diameter 1 mm. Conductor B is a hollow tube of outer diameter 2 mm and inner diameter 1 mm. Find the ratio of resistance RA to RB.
Resistance of wire R = ρ l/A Where A is the cross-sectional area of the conductor L is the length of the conductor ρ is the specific resistance RA = ρl/π(10-3 × 0.5)2 RB = ρl/ π[10-3)2 × (0.5 ×...
Two cells of same emf E but internal resistance r1 and r2 are connected in series to an external resistor R. What should be the value of R so that the potential difference across the terminals of the first cell becomes zero.
Effective emf of two cells = E + E = 2E Effective resistance = R + r1 + r2 Electric current is given as I = 2E/R+r1+r2 Potential difference is given as V1 – E – Ir1 = 0 Which f=gives R = r1 –...
The circuit in the figure shows two cells connected in opposition to each other. Cell E1 is of emf 6V and internal resistance 2Ω; the cell E2 is of emf 4V and internal resistance 8 Ω. Find the potential difference between the points A and B.
Applying Ohm’s law, equivalent emf of the two cells = 6 – 4 = 2V Equivalent resistance = 2 + 8 = 10 Ω Electric current, I = 6-4/2+8 = 0.2A When the loop is considered in the anti-clockwise...
An infinitely long cylinder of radius R is made of an unusual exotic material with refractive index –1. The cylinder is placed between two planes whose normals are along the y-direction. The centre of the cylinder O lies along the y-axis. A narrow laser beam is directed along the y-direction from the lower plate. The laser source is at a horizontal distance x from the diameter in the y-direction. Find the range of x such that light emitted from the lower plane does not reach the upper plane.
The refractive index of the cylinder is -1 and is placed in the air of μ = 1 AB is incident at B to the cylinder such that θr will be negative θ1= θi = θr Total deviation of the outcoming ray is...
If light passes near a massive object, the gravitational interaction causes a bending of the ray. This can be thought of as happening due to a change in the effective refractive index of the medium given by n(r) = 1 + 2 GM/rc2 where r is the distance of the point of consideration from the centre of the mass of the massive body, G is the universal gravitational constant, M the mass of the body and c the speed of light in vacuum. Considering a spherical object find the deviation of the ray from the original path as it grazes the object.
n(r) = 1 + 2GM/rc2
The mixture a pure liquid and a solution in a long vertical column (i.e, horizontal dimensions << vertical dimensions) produces diffusion of solute particles and hence a refractive index gradient along the vertical dimension. A ray of light entering the column at right angles to the vertical deviates from its original path. Find the deviation in travelling a horizontal distance d << h, the height of the column.
Let the height of the long vertical column with transparent liquid be h and dx be the thickness The angle at which the ray AB enters is θ Let y be the new height of the liquid (θ + d θ) is the...
A myopic adult has a far point at 0.1 m. His power of accomodation is 4 diopters. (i) What power lenses are required to see distant objects? (ii) What is his near point without glasses? (iii) What is his near point with glasses? (Take the image distance from the lens of the eye to the retina to be 2 cm.)
i) Power lenses are required to see distant objects 1/f = 1/v – 1/u 1/f = 1/10 f = -10 cm = -0.1 m P = 1/f P = 1/(-0.1) P = -10 diopter ii) When no corrective lens used Pn = Pf + Pa u = -10 cm =...
In many experimental set-ups the source and screen are fixed at a distance say D and the lens is movable. Show that there are two positions for the lens for which an image is formed on the screen. Find the distance between these points and the ratio of the image sizes for these two points.
u = -x1 v = +(D – x1) 1/D – x1 – 1/(-x1) = 1/f u = -x2 v = +(D – x2) 1/D – x2 – 1/(-x2) = 1/f D = x1 + x2 d = x2 – x1 x1 = D – d/2 D – x1 = D + d/2 u = D/2 + d/2 v = D/2 – d/2 m1 = D – d/D + d m2/m1...
A thin convex lens of focal length 25 cm is cut into two pieces 0.5 cm above the principal axis. The top part is placed at (0,0) and an object placed at (–50 cm, 0). Find the coordinates of the image.
1/v = 1/u + 1/f = 1/-50 + 1/25 = 1/50 v = 50 cm Magnification is m = v/u = -50/50 = -1 Therefore, the coordinates of the image are (50 cm, -1 cm) ...
A circular disc of radius ‘R’ is placed co-axially and horizontally inside an opaque hemispherical bowl of radius ‘a’. The far edge of the disc is just visible when viewed from the edge of the bowl. The bowl is filled with transparent liquid of refractive index µ and the near edge of the disc becomes just visible. How far below the top of the bowl is the disc placed?
Distance at which the bowl should be placed in the disc is given as: d = μ(a2 – b2)/√(a + r)2 – μ(a – r)2
There are certain material developed in laboratories which have a negative refractive index (Fig. 9.3). A ray incident from the air (medium 1) into such a medium (medium 2) shall follow a path given by
Answer: (a) The speed of the car in the rear is 65 km h–1. Negative refractive index materials react to Snell's law in the exact opposite direction. When a...
You are given four sources of light each one providing a light of a single colour- red, blue, green, and yellow. Suppose the angle of refraction for a beam of yellow light corresponding to a particular angle of incidence at the interface of two media is 90o. Which of the following statements is correct if the source of yellow light is replaced with that of other lights without changing the angle of incidence?
a) the beam of red light would undergo total internal reflection
b) the beam of red light would bend towards normal while it gets refracted through the second medium
c) the beam of blue light would undergo total internal reflection
d) the beam of green light would bend away from the normal as it gets refracted through the second medium
Answer: c) the beam of blue light would undergo total internal reflection
A ray of light incident at an angle θ on a refracting face of a prism emerges from the other face normally. If the angle of the prism is 5o and the prism is made of a material of refractive index 1.5, the angle of incidence is
a) 7.5o
b) 5o
c) 15o
d) 2.5o
Answer: a) 7.5o The distance between the refracting surfaces is negligible with thin prisms, thus the prism angle (A) is very small. Because A = r1 + r2, if A is tiny, both r1 and r2 will be little...
Two cells of same emf E but internal resistance r1 and r2 are connected in series to an external resistor R. What should be the value of R so that the potential difference across the terminals of the first cell becomes zero.
Effective emf of two cells = E + E = 2E Effective resistance = R + r1 + r2 Electric current is given as I = 2E/R+r1+r2 Potential difference is given as V1 – E – Ir1 = 0 Which f=gives R = r1 –...
Let there be n resistors R1……..Rn with Rmax = max(R1……Rn) and Rmin = min(R1…….Rn). Show that when they are connected in parallel, the resultant resistance Rp < Rmin and when they are connected in series, the resultant resistance Rs > Rmax. Interpret the result physically.
The current is represented as I = E/R+nR when the resistors are connected in series. Current is expressed as 10I = E/(R+R/n) when the resistors are connected in parallel....
First, a set of n equal resistors of R each are connected in series to a battery of emf E and internal resistance R. A current I is observed to flow. Then the n resistors are connected in parallel to the same battery. It is observed that the current is increased 10 times. What is ‘n’?
The current is represented as I = E/R+nR when the resistors are connected in series. Current is expressed as 10I = E/(R+R/n) when the resistors are connected in parallel. We get n = 10 by solving...
. A cell of emf E and internal resistance r is connected across an external resistance R. Plot a graph showing the variation of PD across R versus R.
The graphic depiction is as follows: The resistance r is connected across the external resistance R, and E is the cell's emf. V = ER/R+r is the connection between voltage and R....
While doing an experiment with potentiometer it was found that the deflection is one-sided and i) the deflection decreased while moving from one end A of the wire to the end B; ii) the deflection increased, while the jockey was moved towards the end B. i) Which terminal +ve or –ve of the cell E, is connected at X in case
i) and how is E1 related to E?
ii) Which terminal of the cell E1 is connected at X in case ii)?
The positive terminal of cell E1 is linked to E, and E is connected to X. Furthermore, E1 > E ii) cell E1's negative terminal is linked to X.
Power P is to be delivered to a device via transmission cables having resistance Rc. If V is the voltage across R and I the current through it, find the power wasted and how can it be reduced.
P = i2Rc is the power utilised by transmission lines. The resistance of connecting wires is denoted by Rc. P = VI is the formula for calculating power. Power...
Power P is to be delivered to a device via transmission cables having resistance Rc. If V is the voltage across R and I the current through it, find the power wasted and how can it be reduced.
Power consumed by the transmission lines is given as P = i2Rc. Where Rc is the resistance of connecting cables. Power is given as P = VI. The transmission of power takes places either during low...
Why are alloys used for making standard resistance coils?
Alloys are used in the making of the standard resistance coils because they have less temperature coefficient of resistance and the temperature sensitivity is also less.
For wiring in the home, one uses Cu wires or Al wires. What considerations are involved in this?
The main considerations in the selection of the wires is the conductivity of the metal, cost of metal, and their availability.
What is the advantage of using thick metallic strips to join wires in a potentiometer?strips to join wires in a potentiometer?
The advantage of using thick metallic strips is that the resistance of these strips is negligible.
What are the advantages of the null-point method in a Wheatstone bridge? What additional measurements would be required to calculate R unknown by any other?
The advantage of a null-point in the Wheatstone bridge is that the resistance of the galvanometer is not affected by the balance point. The R unknown is calculated by using Kirchhoff’s rule.
The relaxation time τ is nearly independent of applied E field whereas it changes significantly with temperature T. First fact is responsible for Ohm’s law whereas the second fact leads to a variation of ρ with temperature. Elaborate why?
Relaxation time is the time interval between two successive collisions of the electrons.It is defined asτ = mean free path/rms velocity of electrons usually, the drift velocity of the electrons is...
Is the momentum conserved when charge crosses a junction in an electric circuit? Why or why not?
The momentum is not conserved when the charge crosses a junction in an electric circuit. This is because the drift velocity is proportional to the electric field.
Temperature dependence of resistivity ρ(T) of semiconductors, insulators, and metals is significantly based on the following factors:
a) number of charge carriers can change with temperature T
b) time interval between two successive collisions can depend on T
c) length of material can be a function of T
d) mass of carriers is a function of T
The correct answer is a) number of charge carriers can change with temperature T b) time interval between two successive collisions can depend on T
In a meter bridge, the point D is a neutral point.
a) the meter bridge can have no other neutral point for this set of resistances
b) when the jockey contacts a point on meter wire left of D, current flows to B from the wire
c) when the jockey contacts a point on a meter wire to the right of D, current flows from B to the wire through the galvanometer
d) when R is increased, the neutral point shifts to left
The correct answer is a) the meter bridge can have no other neutral point for this set of resistances c) when the jockey contacts a point on a meter wire to the right of D, current flows from B to...
Temperature dependence of resistivity ρ(T) of semiconductors, insulators, and metals is significantly based on the following factors:
a) number of charge carriers can change with temperature T
b) time interval between two successive collisions can depend on T
c) length of material can be a function of T
d) mass of carriers is a function of T
solution:The correct answer is a) number of charge carriers can change with temperature T b) time interval between two successive collisions can depend on T
Consider a simple circuit in the figure.stands for a variable resistance R’.
R’ can vary from R0 to infinity. r is internal resistance of the battery,
a) potential drop across AB is nearly constant as R’ is varied
b) current through R’ is nearly a constant as R’ is varied
c) current I depends sensitively on R’
d) I ≥V/r+R always
solution: The correct answer is a) potential drop across AB is nearly constant as R’ is varied d) I ≥V/r+R always
Kirchhoff’s junction rule is a reflection of
a) conservation of current density vector
b) conservation of charge
c) the fact that the momentum with which a charged particle approaches a junction is unchanged as the charged particle leaves the junction
d) the fact that there is no accumulation of charges at a junction
solution: The correct answer is b) conservation of charge d) the fact that there is no accumulation of charges at a junction
Which of the following characteristics of electrons determines the current in a conductor?
v a) drift velocity alone
b) thermal velocity alone
c) both drift velocity and thermal velocity
d) neither drift nor thermal velocity
solution: The correct answer is a) drift velocity alone
A metal rod of length 10 cm and a rectangular cross-section of 1 cm × 1/2 cm is connected to battery across opposite faces. The resistance will be
a) maximum when the battery is connected across 1 cm × 1/2 cm faces
b) maximum when the battery is connected across 10 cm × 1 cm faces
c) maximum when the battery is connected across 10 cm × 1/2 cm faces
d) same irrespective of the three faces
solution:The correct solution is a) maximum when the battery is connected across 1 cm × 1/2 cm faces
Two cells of emf’s approximately 5V and 10V are to be accurately compared using a potentiometer of length 400 cm.
a) the battery that runs the potentiometer should have voltage of 8V
b) the battery of potentiometer can have a voltage of 15V and R adjusted so that the potential drop across the wire slightly exceeds 10V
c) the first portion of 50 cm of wire itself should have a potential drop of 10V
d) potentiometer is usually used for comparing resistances and not voltages
Solution: The correct solution is b) the potentiometer's battery can be set to 15V and R adjusted so that the potential drop across the wire is a little higher than 10V.
A resistance R is to be measured using a meter bridge. Student chooses the standard resistance S to be 100Ω. He finds the null point at l1 = 2.9 cm . He is told to attempt to improve the accuracy. Which of the following is a useful way?
a) he should measure l1 more accurately
b) he should change S to 1000 Ω and repeat the experiment
c) he should change S to 3 Ω and repeat the experiment
d) he should give up hope of a more accurate measurement with a meter bridge
solution:The correct answer is c) he should change S to 3 Ω and repeat the experiment
Two batteries of emf ε1 and ε2 and internal resistances r1 and r2 respectively are connected in parallel as shown in the figure.a) the equivalent emf εeq of the two cells is between ε1 and ε2 that is ε1 < εeq < ε2
b) the equivalent emf εeq is smaller than ε1
c) the εeq is given by εeq = ε1 + ε2 always
d) εeq is independent of internal resistances r1 and r2
solution: The correct answer is a) the equivalent emf εeq of the two cells is between ε1 and ε2 that is ε1 < εeq < ε2
Consider a current-carrying wire in the shape of a circle. Note that as the current progresses along the wire, the direction of j changes in an exact manner, while the current I remain unaffected. The agent that is essentially responsible for is
a) source of emf
b) electric field produced by charges accumulated on the surface of wire
c) the charges just behind a given segment of wire which push them just the right way by repulsion
d) the charges ahead
solution: The correct answer is b) electric field produced by charges accumulated on the surface of wire
Consider a ray of light incident from air onto a slab of glass (refractive index n) of width d, at an angle θ. The phase difference between the ray reflected by the top surface of the glass and the bottom surface is (a) 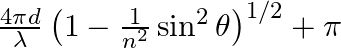 (b)
(b) 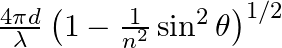 (c)
(c) 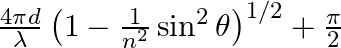 (d)
(d) 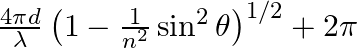
The correct answer is a) $ \frac{4 \pi d}{\lambda}\left(1-\frac{1}{n^{2}} \sin ^{2} \theta\right)^{1 / 2}+\pi $ Explanation: When a slab of glass is put in air, the wave reflected from the upper...
Can reflection result in plane-polarized light if the light is incident on the interface from the side with higher refractive index?
When the angle of incidence is equal to the Brewster's angle, polarised light is transmitted and plane-polarized light is reflected. The equation is as follows: $ \tan...
The figure shown a two-slit arrangement with a source which emits unpolarised light. P is a polariser with axis whose direction is not given. If I0 is the intensity of the principal maxima when no polarizer is present, calculate in the present case, the intensity of the principal maxima as well as of the first minima.
Given wave amplitude in perpendicular polarisation $ A_{\perp}=A_{\perp}^{0}(\sin (k x-\omega t)+\sin (k x-\omega t+\phi)) $ wave amplitude in parallel polarisation $ A_{\|}=A_{\|}^{0}(\sin (k...
AC = CO = D, S1 C = S2 C = d << D A small transparent slab containing material of µ =1.5 is placed along AS2. What will be the distance from O of the principal maxima and of the first minima on either side of the principal maxima obtained in the absence of the glass slab?
According to the question, $ \begin{array}{l} \Delta x=2 d \sin \theta+(\mu-1) L \\ \sin \theta 0=-1 / 16 \end{array} $ From central maxima, $O P=-D / 16$ $ \sin \theta_{1}=\frac{\pm \lambda / 2-d /...
The output of the given circuit in the figure
(a) would be zero at all times (b) would be like a half-wave rectifier with positive cycles in output (c) would be like a half-wave rectifier with negative cycles in output (d) would be like that of...
The Bohr model for the H-atom relies on the Coulomb’s law of electrostatics. Coulomb’s law has not directly been verified for very short distances of the order of angstroms. Supposing Coulomb’s law between two opposite charge 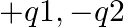 is modified to
is modified to 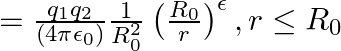 Calculate in such a case, the ground state energy of an
Calculate in such a case, the ground state energy of an  atom, if
atom, if 
Case 1: When $\varepsilon=0.1, \mathrm{R_O}=1 \mathrm{~A}$ $\mathrm R_1=8 \times 10^{-11}$ $\mathrm{M}=0.08 \mathrm{~nm}$ Velocity at ground level is given as $\mathrm v_1=1.44 \times 10^{6}...
The inverse square law in electrostatics is 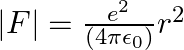 for the force between an electron and a proton. The
for the force between an electron and a proton. The  dependence of
dependence of  can be understood in quantum theory as being due to the fact that the ‘particle’ of light (photon) is massless. If photons had a mass
can be understood in quantum theory as being due to the fact that the ‘particle’ of light (photon) is massless. If photons had a mass  , force would be modified to
, force would be modified to ![Rendered by QuickLaTeX.com |F|=\frac{e^{2}}{\left(4 \pi \epsilon_{0}\right)} r^{2}\left[\frac{1}{r^{2}}+\frac{\lambda}{r}\right] \quad](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-514ad8afbf25cd57a0bc62f92316ce07_l3.png) where
where 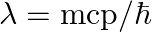 and
and 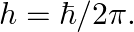 Estimate the change in the ground state energy of an H-atom if
Estimate the change in the ground state energy of an H-atom if 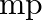 were
were 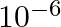 times the mass of an electron.
times the mass of an electron.
$m_{\mathrm{p}} c^{2}=10^{-6} \times$ electron mass $\times c^{2}$ $=10^{-6} \times 0.5 \mathrm{MeV}$ $\approx 10^{-6} \times 0.5 \times 1.6 \times 10^{-13}$ $\approx \mathrm{O} .8 \times 1...
In the Auger process, an atom makes a transition to a lower state without emitting a photon. The excess energy is transferred to an outer electron which may be ejected by the atom. (This is called an Auger electron). Assuming the nucleus to be massive, calculate the kinetic energy of an 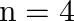 Auger electron emitted by Chromium by absorbing the energy from an
Auger electron emitted by Chromium by absorbing the energy from an 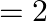 to
to 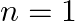 transition.
transition.
The energy in the nth state can be calculated as, $-\operatorname{Rch} Z^{2} / n^{2}=-13.6 z^{2} / n^{2} e V$ Where $R=$ Rydberg constant and $\mathrm{Z}=24$ Energy released is given as $\left(13.6...
Deuterium was discovered in 1932 by Harold Urey by measuring the small change in wavelength for a particular transition in 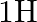 and
and 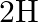 . This is because the wavelength of transition depends to a certain extent on the nuclear mass. If nuclear motion is taken into account then the electrons and nucleus revolve around their common centre of mass. Such a system is equivalent to a single particle with a reduced mass
. This is because the wavelength of transition depends to a certain extent on the nuclear mass. If nuclear motion is taken into account then the electrons and nucleus revolve around their common centre of mass. Such a system is equivalent to a single particle with a reduced mass 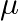 , revolving around the nucleus at a distance equal to the electron-nucleus separation. Here
, revolving around the nucleus at a distance equal to the electron-nucleus separation. Here 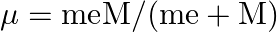 where
where 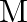 is the nuclear mass and
is the nuclear mass and 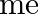 is the electronic mass. Estimate the percentage difference in wavelength for the 1 st line of the Lyman series in
is the electronic mass. Estimate the percentage difference in wavelength for the 1 st line of the Lyman series in 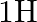 and
and 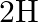 . (Mass of
. (Mass of 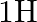 nucleus is
nucleus is 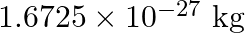 , Mass of
, Mass of 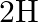 nucleus is
nucleus is 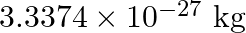 , Mass of electron
, Mass of electron 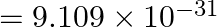 kg.)
kg.)
The energy of an electron in the nth state is given by the expression, $E_ n=-\mu Z^{2} \mathrm{e}^{4} / 8 \varepsilon_ 0^{2} h^{2}\left(1 / n^{2}\right)$ For hydrogen atom we have, $\mu...
The first four spectral lines in the Lyman series of an H-atom are 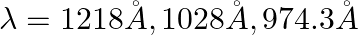 and
and 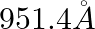 . If instead of Hydrogen, we consider Deuterium, calculate the shift in the wavelength of these lines.
. If instead of Hydrogen, we consider Deuterium, calculate the shift in the wavelength of these lines.
Let the reduced masses of electrons of hydrogen and deuteriur be $\mu _{H}$ and $\mu _{D}$ The fixed mass series for hydrogen and deuterium be $n_i$ and $n_f$ $R_h / R_d=\mu _H / \mu _D$ Reduced...
What is the minimum energy that must be given to an  atom in ground state so that it can emit an Hy line in Balmer series? If the angular momentum of the system is conserved, what would be the angular momentum of such Hy photon?
atom in ground state so that it can emit an Hy line in Balmer series? If the angular momentum of the system is conserved, what would be the angular momentum of such Hy photon?
Energy required for the transition from $n=1$ to $n=5$ can be calculated as, $E=E _5-E_ 1=\left(-13.6 / 5^{2}\right)-\left(-13.6 / 1^{2}\right)=13.06 \mathrm{eV}$ Angular momentum is given as change...
Show that the first few frequencies of light that are emitted when electrons fall to the  th level from levels higher than
th level from levels higher than 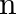 are approximate harmonics (i.e. in the ratio
are approximate harmonics (i.e. in the ratio 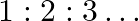 ) when
) when 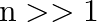 .
.
The difference between the two atoms is used to indicate the frequency of any line in the hydrogen spectrum series. $\mathrm{f_{cm}}=\mathrm{cRZ}^{2}\left[1 /(\mathrm{n}+\mathrm{p})^{2}-1 /...
Using the Bohr model, calculate the electric current created by the electron when the H-atom is in the ground state.
Let the velocity of the electron be $v$ Number of revolutions per unit time is given as $\mathrm{f}=2 \mathrm{ma}_{0} / \mathrm{V}$ The electric current is given as $I=Q$ When change $Q$ flows in...
Assume that there is no repulsive force between the electrons in an atom but the force between positive and negative charges is given by Coulomb’s law as usual. Under such circumstances, calculate the ground state energy of a He-atom.
For He nucleus we have, $Z=2$ and in ground state, $n=1$ As a result, $E n=-13.6 Z^{2} / n^{2} e V=-54.4 \mathrm{eV}$
Positronium is just like an H-atom with the proton replaced by the positively charged anti-particle of the electron (called the positron which is as massive as the electron). What would be the ground state energy of positronium?
The positronium has the lowest energy of -6.8 electron volts. The greatest energy level of positronium is -1.7 electron volt, which is the next highest energy level after n = 1.
Consider two different hydrogen atoms. The electron in each atom is in an excited state. Is it possible for the electrons to have different energies but the same orbital angular momentum according to the Bohr model?
Because the value of n in two hydrogen atoms differs, their angular momentum differs as well. The angular momentum, according to Bohr's model, is given as L = nh/2π
The mass of H atom is less than sum of the masses of a proton and electron. Why is this?
Protons and neutrons (and other particles) are held together by something called the strong nuclear force (strong interaction). This force diminishes the system's overall energy, which is dissipated...
Let 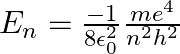 be the energy of the nth level of H-atom. If all the H-atoms are in the ground state and radiation of frequency
be the energy of the nth level of H-atom. If all the H-atoms are in the ground state and radiation of frequency 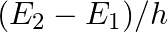 falls on it
falls on it
(a) it will not be absorbed at all
(b) some of the atoms will move to the first excited state
(c) all atoms will be excited to the  state
state
(d) no atoms will make a transition to the  state
state
The correct options are: (b) some of the atoms will move to the first excited state (d) no atoms will make a transition to the $n=3$ state
The Balmer series for the H-atom can be observed
(a) if we measure the frequencies of light emitted when an excited atom falls to the ground state
(b) if we measure the frequencies of light emitted due to transitions between excited states and the first excited state
(c) in any transition in a  -atom
-atom
(d) as a sequence of frequencies with the higher frequencies getting closely packed
The correct options are: (b) if we measure the frequencies of light emitted due to transitions between excited states and the first excited state (d) as a sequence of frequencies with the higher...
The Bohr model for the spectra of an H-atom
(a) will not be applicable to hydrogen in the molecular from
(b) will not be applicable as it is for a He-atom
(c) is valid only at room temperature
(d) predicts continuous as well as discrete spectral lines
The correct options are: (a) will not be applicable to hydrogen in the molecular from (b) will not be applicable as it is for a $\mathrm{He}$-atom
Consider aiming a beam of free electrons towards free protons. When they scatter, an electron and a proton cannot combine to produce an H-atom,
(a) because of energy conservation
(b) without simultaneously releasing energy in the form of radiation
(c) because of momentum conservation
(d) because of angular momentum conservation
The correct options are: (a) because of energy conservation (b) without simultaneously releasing energy in the form of radiation
An ionised H-molecule consists of an electron and two protons. The protons are separated by a small distance of the order of angstrom. In the ground state,
(a) the electron would not move in circular orbits
(b) the energy would be (2) 4 times that of an 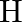 -atom
-atom
(c) the electrons, the orbit would go around the protons
(d) the molecule will soon decay in a proton and an 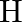 -atom
-atom
The correct options are: (a) the electron would not move in circular orbits (c) the electrons, the orbit would go around the protons
A set of atoms in an excited state decays.
(a) in general to any of the states with lower energy
(b) into a lower state only when excited by an external electric field
(c) all together simultaneously into a lower state
(d) to emit photons only when they collide
The correct option is: (a) in general to any of the states with lower energy
Two H atoms in the ground state collide inelastically. The maximum amount by which their combined kinetic energy is reduced is
(a) 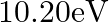
(b) 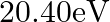
(c) 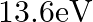
(d) 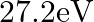
The correct option is: (a) $10.20 \mathrm{eV}$
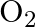 molecule consists of two oxygen atoms. In the molecule, nuclear force between the nuclei of the two atoms
molecule consists of two oxygen atoms. In the molecule, nuclear force between the nuclei of the two atoms
(a) is not important because nuclear forces are short-ranged
(b) is as important as an electrostatic force for binding the two atoms
(c) cancels the repulsive electrostatic force between the nuclei
(d) is not important because the oxygen nucleus have an equal number of neutrons and protons
The correct option is: (a) is not important because nuclear forces are short-ranged
For the ground state, the electron in the H-atom has an angular momentum 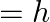 , according to the simple Bohr model. Angular momentum is a vector and hence there will be infinitely many orbits with the vector pointing in all possible directions. In actuality, this is not true,
, according to the simple Bohr model. Angular momentum is a vector and hence there will be infinitely many orbits with the vector pointing in all possible directions. In actuality, this is not true,
(a) because Bohr model gives incorrect values of angular momentum
(b) because only one of these would have a minimum energy
(c) angular momentum must be in the direction of spin of electron
(d) because electrons go around only in horizontal orbits
The correct option is: (a) because Bohr model gives incorrect values of angular momentum
The simple Bohr model cannot be directly applied to calculate the energy levels of an atom with many electrons. This is because
(a) of the electrons not being subject to a central force
(b) of the electrons colliding with each other
(c) of screening effects
(d) the force between the nucleus and an electron will no longer be given by Coulomb’s law
The correct option is: (a) of the electrons not being subject to a central force
The binding energy of an H-atom, considering an electron moving around a fixed nucleus (proton), is 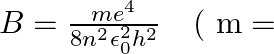 electron mass
electron mass 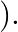 If one decides to work in a frame of reference where the electron is at rest, the proton would be moving around it. By similar arguments, the binding energy would be
If one decides to work in a frame of reference where the electron is at rest, the proton would be moving around it. By similar arguments, the binding energy would be 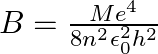 (M = proton mass) This last expression is not correct because
(M = proton mass) This last expression is not correct because
(a) n would not be integral
(b) Bohr-quantisation applies only to electron
(c) the frame in which the electron is at rest is not inertial
(d) the motion of the proton would not be in circular orbits, even approximately
The correct option is: (c) the frame in which the electron is at rest is not inertial
Taking the Bohr radius as 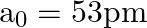 , the radius of
, the radius of 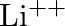 ion in its ground state, on the basis of Bohr’s model, will be about
ion in its ground state, on the basis of Bohr’s model, will be about
(a) 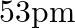
(b) 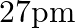
(c) 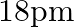
(d) 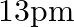
The correct option is: (c) $18 \mathrm{pm}$
Nuclei with magic no. of proton 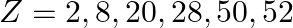 and magic no. of neutrons
and magic no. of neutrons 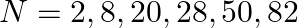 and
and 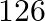 are found to be very stable
are found to be very stable
(i) Verify this by calculating the proton separation energy Sp for 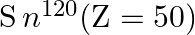 and
and 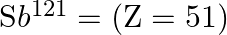 . The proton separation energy for a nuclide is the minimum energy required to separate the least tightly bound proton from a nucleus of that nuclide. It is given by
. The proton separation energy for a nuclide is the minimum energy required to separate the least tightly bound proton from a nucleus of that nuclide. It is given by 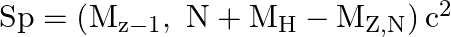 . Given
. Given 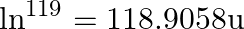 ,
, 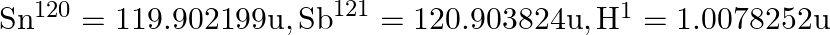
(ii) What does the existence of magic number indicate?
i) The proton separation energy is given by, $\mathrm{SpSn}=(\mathrm{M} 119.70+\mathrm{Mh}-\mathrm{M} 120.70) \mathrm{c}^{2}=0.0114362 \mathrm{c}^{2}$ Similarly we have, $\mathrm{SpSp}=(\mathrm{M}...
The activity 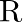 of an unknown radioactive nuclide is measured at hourly intervals. The results found are tabulated as follows:
of an unknown radioactive nuclide is measured at hourly intervals. The results found are tabulated as follows: ![Rendered by QuickLaTeX.com \[\begin{tabular}{|l|l|l|l|l|l|} \hline$t(\mathrm{~h})$ & 0 & 1 & 2 & 3 & 4 \\ \hline R(MBq) & 100 & $35.36$ & $12.51$ & $4.42$ & $1.56$ \\ \hline \end{tabular}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2cff4d33a1ea1a3274f405d5eee59de6_l3.png)
(i) Plot the graph of R versus 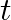 and calculate half-life from the graph.
and calculate half-life from the graph.
(ii) Plot the graph of 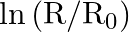 versus
versus 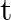 and obtain the value of half-life from the graph.
and obtain the value of half-life from the graph.
![Rendered by QuickLaTeX.com \[\begin{tabular}{|l|l|l|l|l|l|} \hline$t(\mathrm{~h})$ & 0 & 1 & 2 & 3 & 4 \\ \hline R(MBq) & 100 & $35.36$ & $12.51$ & $4.42$ & $1.56$ \\ \hline \end{tabular}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2cff4d33a1ea1a3274f405d5eee59de6_l3.png)
(i) Graph between $\mathrm{R}$ versus $\mathrm{t}$ will be an exponential curve. From the graph at slightly more than $\mathrm{t}=\frac{1}{2} \mathrm{~h}$ the $\mathrm{R}$ should be $50 \%$ so at...
Before the neutrino hypothesis, the beta decay process was thought to be the transition 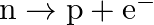 . If this was true, show that if the neutron was at rest, the proton and electron would emerge with fixed energies and calculate them. Experimentally, the electron energy was found to have a large range.
. If this was true, show that if the neutron was at rest, the proton and electron would emerge with fixed energies and calculate them. Experimentally, the electron energy was found to have a large range.
It is given that neutron was at rest before $\beta$ decay from neutron. So, energy of neutron $=$ $\mathrm{E}_{\mathrm{n}}=\mathrm{m}_{\mathrm{n}} \mathrm{c}^{2}$. Momentum of neutron...
The deuteron is bound by nuclear forces just as 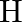 -atom is made up of
-atom is made up of 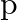 and e bound by electrostatic forces. If we consider the force between neutron and proton in deuteron as given in the form of a Coulomb potential but with an effective charge
and e bound by electrostatic forces. If we consider the force between neutron and proton in deuteron as given in the form of a Coulomb potential but with an effective charge 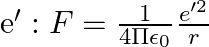 estimate the value of
estimate the value of 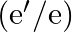 given that the binding energy of a deuteron is
given that the binding energy of a deuteron is 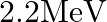 .
.
The binding energy of $\mathrm{H}$ atom is given as $\mathrm{E}=13.6 \mathrm{eV}$ The reduced $\mathrm{m}^{\prime}$ is given as $918 \mathrm{~m}$ The mass of a neutron or a proton is given as...
Deuteron is a bound state of a neutron and a proton with a binding energy B = 2.2 MeV. A γ -ray of energy E is aimed at a deuteron nucleus to try to break it into a (neutron + proton) such that the n and p move in the direction of the incident γ-ray. If E = B, show that this cannot happen. Hence calculate how much bigger than B must E be for such a process to happen.
The binding energy of a deuteron is given as $B = 2.2 MeV$ The kinetic energies of neutron and proton be $K_n$ and $K_p$ $p_n$ and $p_p$ are the momentum of neutron and proton $E - B = K_n + K_p$ B...
Sometimes a radioactive nucleus decays into a nucleus which itself is radioactive. An example is
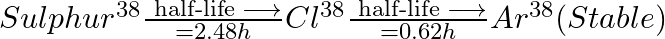
Assume that we start with 1000 38S nuclei at time  . The number of
. The number of 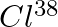 is of count zero at
is of count zero at  and will again be zero at
and will again be zero at 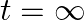 . At what value of
. At what value of 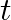 , would the number of counts be a maximum?
, would the number of counts be a maximum?
Let the disintegration constants for $S^{38}$ and $Cl^{38}$ be $\lambda_ 1$ and $\lambda_ 2$ respectively. $\mathrm dN_1 / \mathrm{dt}=-\lambda N_{1}$ $\mathrm dN_2 / \mathrm{dt}=$ rate of decay of...
A nuclide 1 is said to be the mirror isobar of nuclide 2 if 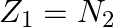 and
and 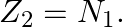
(a) What nuclide is a mirror isobar of 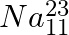 ?
?
(b) Which nuclide out of the two mirror isobars have greater binding energy and why?
a) We are given that a nuclide 1 is to be the mirror isobar of nuclide 2 if, $\mathrm Z_1=\mathrm N_2$ and $\mathrm Z_2=\mathrm N_1$ As a result, mirror isobar is $Z _2=12-N_ 1$ and $N_...
Are the nucleons fundamental particles, or do they consist of still smaller parts? One way to find out is to probe a nucleon just as Rutherford probed an atom. What should be the kinetic energy of an electron for it to be able to probe a nucleon? Assume the diameter of a nucleon to be approximately 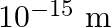 .
.
$\lambda=\mathrm{h} / \mathrm{p}$ and, kinetic energy $=$ potential energy $\mathrm{E}=\mathrm{hc} / \lambda$ Kinetic energy of an electron can be calculated as, $\mathrm{KE}=\mathrm{PE}=\mathrm{hc}...
A piece of wood from the ruins of an ancient building was found to have a 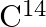 activity of 12 disintegrations per minute per gram of its carbon content. The
activity of 12 disintegrations per minute per gram of its carbon content. The 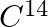 activity of the living wood is 16 disintegrations per minute per gram. How long ago did the tree, from which the wooden sample came, die? Given the half-life of
activity of the living wood is 16 disintegrations per minute per gram. How long ago did the tree, from which the wooden sample came, die? Given the half-life of 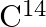 is 5760 years.
is 5760 years.
$\mathrm{C}^{14}$ activity of a piece of wood from the ruins is given as $\mathrm{R}=12 \mathrm{dis} / \mathrm{min}$ per gram $\mathrm{C}^{14}$ activity of a living wood is given as...
Consider a radioactive nucleus A which decays to a stable nucleus 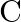 through the following sequence:
through the following sequence: 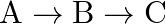 Here
Here 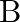 is an intermediate nuclei which is also radioactive. Considering that there are
is an intermediate nuclei which is also radioactive. Considering that there are 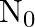 atoms of A initially, plot the graph showing the variation of number of atoms of
atoms of A initially, plot the graph showing the variation of number of atoms of  and
and  versus time.
versus time.
At $\mathrm{t}=0,$ $\mathrm{~N}_{\mathrm{A}}=\mathrm{N}_{0}$ As time passes, $N_A$ decreases exponentially, while the number of atoms in B increases, reaches its maximum, and then decays to...
Why do stable nuclei never have more protons than neutrons?
Because protons are charged particles that resist one other, stable nuclei never have more protons than neutrons. Because of the strong repulsion, extra neutrons only produce attractive forces,...
In pair annihilation, an electron and a positron destroy each other to produce gamma radiation. How is the momentum conserved?
An electron and a positron kill one other to produce gamma radiation in pair annihilation. Also, their momentum is conserved because they move in opposing directions.
Which one of the following cannot emit radiation and why? Excited nucleus, excited electron.
Because the energy of the electronic energy level is in the eV range rather than the MeV range, an excited electron cannot release radiation.
Which sample, A or B shown in the figure has shorter mean-life?
Solution: At t=0, $(d N / d t) A=(d N / d t) B$ $d N / d t=-\lambda N$ $\left(N_{0}\right) A=\left(N_{0}\right) B$ $\lambda_ A N_ A=\lambda_ B N_ B$ $N_ a>N_ B$ $\lambda_ B>\lambda_ A$
Draw a graph showing the variation of decay rate with number of active nuclei.
According to Rutherford and Soddy law, the radioactive decay is given as –dN/dt = λN.
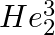 and
and 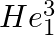 nuclei have the same mass number. Do they have the same binding energy?
nuclei have the same mass number. Do they have the same binding energy?
Despite the fact that $H e_{2}^{3}$ and $H e_{1}^{3}$ have the same mass number, their binding energies are different. Because the number of protons and neutrons in both nuclei differs, the binding...
The variation of the decay rate of two radioactive samples A and B with time is shown in the figure. Which of the following statements are true?
(a) The decay constant of A is greater than that of B, hence A always decays faster than B (b) The decay constant of B is greater than that of A but its decay rate is always smaller than that of A...
Samples of two radioactive nuclides A and B are taken. 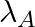 and
and 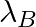 are the disintegration constants of A and B respectively. In which of the following cases, the two samples can simultaneously have the same decay rate at any time?
are the disintegration constants of A and B respectively. In which of the following cases, the two samples can simultaneously have the same decay rate at any time?
(a) Initial rate of decay of A is twice the initial rate of decay of B and 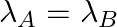
(b) Initial rate of decay of A is twice the initial rate of decay of B and 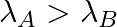
(c) Initial rate of decay of B is twice the initial rate of decay of A and 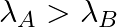
(d) Initial rate of decay of B is the same as the rate of decay of A at  and
and 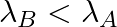
The correct options are: (b) Initial rate of decay of A is twice the initial rate of decay of B and $\lambda _A>\lambda_B$ (d) Initial rate of decay of B is the same as the rate of decay of A at...
Fusion processes, like combining two deuterons to form a He nucleus are impossible at ordinary temperatures and pressure. The reasons for this can be traced to the fact:
(a) nuclear forces have short-range
(b) nuclei are positively charged
(c) the original nuclei must be completely ionized before fusion can take place
(d) the original nuclei must first break up before combining with each other
The correct options are: (a) nuclear forces have short-range (b) nuclei are positively charged
In a nuclear reactor, moderators slow down the neutrons which come out in a fission process. The moderator used to have light nuclei. Heavy nuclei will not serve the purpose because
(a) they will break up
(b) elastic collision of neutrons with heavy nuclei will not slow them down
(c) the net weight of the reactor would be unbearably high
(d) substances with heavy nuclei do not occur in a liquid or gaseous state at room temperature
The correct option is: (b) elastic collision of neutrons with heavy nuclei will not slow them down
Heavy stable nuclei have more neutrons than protons. This is because of the fact that
(a) neutrons are heavier than protons
(b) electrostatic force between protons are repulsive
(c) neutrons decay into protons through beta decay
(d) nuclear forces between neutrons are weaker than that between protons
The correct option is: (b) electrostatic force between protons are repulsive
Tritium is an isotope of hydrogen whose nucleus Triton contains 2 neutrons and 1 proton. Free neutrons decay into 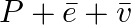 . If one of the neutrons in Triton decays, it would transform into He3 nucleus. This does not happen. This is because
. If one of the neutrons in Triton decays, it would transform into He3 nucleus. This does not happen. This is because
(a) Triton energy is less than that of a 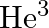 nucleus
nucleus
(b) the electron created in the beta decay process cannot remain in the nucleus
(c) both the neutrons in triton have to decay simultaneously resulting in a nucleus with 3 protons, which is not a 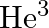 nucleus
nucleus
(d) because free neutrons decay due to external perturbations which is absent in a triton nucleus
The correct option is: (a) Triton energy is less than that of a $\mathrm{He}^{3}$ nucleus
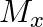 and
and 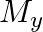 denote the atomic masses of the parent and the daughter nuclei respectively in a radioactive decay. The Q-value for a
denote the atomic masses of the parent and the daughter nuclei respectively in a radioactive decay. The Q-value for a 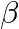 – decay is
– decay is  and that for a
and that for a 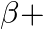 decay is
decay is  . If me denotes the mass of an electron, then which of the following statements is correct?
. If me denotes the mass of an electron, then which of the following statements is correct?
(a) 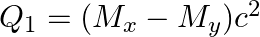 and
and 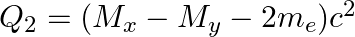
(b) 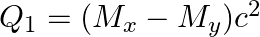 and
and 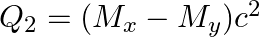
(c) 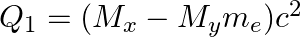 and
and 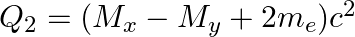
(d) 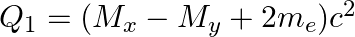 and
and 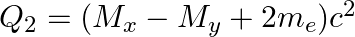
The correct option is: (a) $Q_ 1=(M _x-M_ y) c^{2}$ and $Q_ 2=(M _x-M_ y-2 m_ e) c^{2}$
When a nucleus in an atom undergoes radioactive decay, the electronic energy levels of the atom
(a) do not change for any type of radioactivity
(b) change for α and β radioactivity but not for γ-radioactivity
(c) change for α-radioactivity but not for others
(d) change for β-radioactivity but not for others
The correct option is: (b) change for α and β radioactivity but not for γ-radioactivity
The gravitational force between an H-atom and another particle of mass m will be given by Newton’s law: 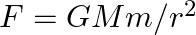 , where r is in km and
, where r is in km and
(a) M = mproton + m electron
(b) M = mproton 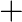 melectron
melectron 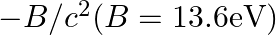
(c) M is not related to the mass of the hydrogen atom
(d) M = mproton +melectron 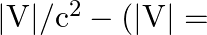 magnitude of the potential energy of electron in the
magnitude of the potential energy of electron in the 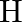 -atom)
-atom)
The correct option is: (b) M = mproton $+$ melectron $-B / c^{2}(B=13.6 \mathrm{eV})$
Suppose we consider a large number of containers each containing initially 10000 atoms of a radioactive material with a half-life of 1 year. After 1 year
(a) all the containers will have 5000 atoms of the material
(b) all the containers will contain the same number of atoms of the material but that number will only be approximately 5000
(c) the containers will, in general, have different numbers of the atoms of the material but their average will be close to 5000
(d) none of the containers can have more than 5000 atoms
The correct option is: (c) the containers will, in general, have different numbers of the atoms of the material but their average will be close to 5000
If the total charge enclosed by a surface is zero, does it imply that the electric field everywhere on the surface is zero? Conversely, if the electric field everywhere on a surface is zero, does it imply that net charge inside is zero.
Although a surface's total charge is zero, this does not imply that the electric field is zero everywhere on the surface; the field may be normal to the surface. In addition, it implies that the...
The dimensions of an atom are of the order of an Angstrom. Thus there must be large electric fields between the protons and electrons. Why, then is the electrostatic field inside a conductor zero?
Because the dimensions of an atom are on the order of an Angstrom, the electrostatic field within a conductor is zero, and the electrostatic field inside the conductor is created by the presence of...
A metallic spherical shell has an inner radius R1 and outer radius R2. A charge Q is placed at the centre of the spherical cavity. What will be surface charge density on a) the inner surface b) the outer surface
Q is the charge which is kept at the centre of the spherical cavity. –Q is the charge that is induced in the inner surface and –Q on the outer surface. σ is the surface charge density a) σ1 is the...
An arbitrary surface encloses a dipole. What is the electric flux through this surface?
According to Gauss law, for an enclosed surface, the electric flux is given as: $\oint_{s} \underset{E} \cdot d \frac{q_{e n c l o s e d}}{\epsilon_{0}}$ The net charge on the dipole is given as...
A positive charge Q is uniformly distributed along a circular ring of radius R. A small test charge q is placed at the centre of the ring. Then a) if q > 0 and is displaced away from the centre in the plane of the ring., it will be pushed back towards the centre b) if q < 0 and is displaced away from the centre in the plane of the ring, it will never return to the centre and will continue moving till it hits the ring c) if q < 0, it will perform SHM for small displacement along the axis d) q at the centre of the ring is in an unstable equilibrium within the plane of the ring for q > 0
The correct options are a) if q > 0 and is displaced away from the centre in the plane of the ring., it will be pushed back towards the centre b) if q < 0 and is displaced away from the centre...
Refer to the arrangement of charges in the figure and a Gaussian surface of radius R with Q at the centre. Then a) total flux through the surface of the sphere is –Q/ε0 b) field on the surface of the sphere is –Q/4πε0R2 c) flux through the surface of the sphere due to 5Q is zero d) field on the surface of the sphere due to -2Q is the same everywhere
The correct options are a) total flux through the surface of the sphere is –Q/ε0 c) flux through the surface of the sphere due to 5Q is zero
Consider a region inside which there are various types of charges but the total charge is zero. At points outside the region a) the electric field is necessarily zero b) the electric field is due to the dipole moment of the charge distribution only c) the dominant electric field is proportional to 1/r3 for large r, where r is the distance from an origin in this region d) the work done to move a charged particle along a closed path, away from the region, will be zero
The correct options are c) the dominant electric field is proportional to 1/r3 for large r, where r is the distance from an origin in this region d) the work done to move a charged particle along a...
The electric field at a point is a) always continuous b) continuous if there is no charge at that point c) discontinuous only if there is a negative charge at that point d) discontinuous if there is a charge at that point
The correct options are b) continuous if there is no charge at that point d) discontinuous if there is a charge at that point
If  over a surface, then a) the electric field inside the surface and on it is zero b) the electric field inside the surface is necessarily uniform c) the number of flux lines entering the surface must be equal to the number of flux lines leaving it d) all charges must necessarily be outside the surface
over a surface, then a) the electric field inside the surface and on it is zero b) the electric field inside the surface is necessarily uniform c) the number of flux lines entering the surface must be equal to the number of flux lines leaving it d) all charges must necessarily be outside the surface
The correct options are c) the number of flux lines entering the surface must be equal to the number of flux lines leaving it d) all charges must necessarily be outside the surface
A hemisphere is uniformly charged positively. The electric field at a point on a diameter away from the centre is directed a) perpendicular to the diameter b) parallel to the diameter c) at an angle tilted towards the diameter d) at an angle tilted away from the diameter
The correct option is a) perpendicular to the diameter
A point charge +q is placed at a distance d from an isolated conducting plane. The field at a point P on the other side of the plane is a) directed perpendicular to the plane and away from the plane b) directed perpendicularly to the plane towards the plane c) directed radially away from the point charge d) directed radially towards the point charge
The correct option is a) directed perpendicular to the plane and away from the plane
Figure shows electric field lines in which an electric dipole p is placed as shown. Which of the following statements is correct? a) the dipole will not experience any force b) the dipole will experience a force towards right c) the dipole will experience a force towards left d) the dipole will experience a force upwards
The correct option is c) the dipole will experience a force towards left
Five charges 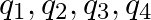 , and
, and 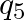 are fixed at their positions as shown in the figure.
are fixed at their positions as shown in the figure. 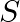 is a Gaussian surface. The Gauss’s law is given by
is a Gaussian surface. The Gauss’s law is given by 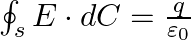 Which of the following statements is correct? a) E on the LHS of the above equation will have a contribution from q1, q3, and q5 while q on the RHS will have a contribution from q2 and q4 only b) E on the LHS of the above equation will have a contribution from all charges while q on the RHS will have a contribution from q2 and q4 only c) E on the LHS of the above equation will have a contribution from all charges while q on the RHS will have a contribution from q1, q3, and q5 only d) both E on the LHS and q on the RHS will have contributions from q2 and q4 onlyv
Which of the following statements is correct? a) E on the LHS of the above equation will have a contribution from q1, q3, and q5 while q on the RHS will have a contribution from q2 and q4 only b) E on the LHS of the above equation will have a contribution from all charges while q on the RHS will have a contribution from q2 and q4 only c) E on the LHS of the above equation will have a contribution from all charges while q on the RHS will have a contribution from q1, q3, and q5 only d) both E on the LHS and q on the RHS will have contributions from q2 and q4 onlyv
The correct option is b) E on the LHS of the above equation will have a contribution from all charges while q on the RHS will have a contribution from q2 and q4 only
The electric flux through the surface a) fig (iv) is the largest b) fig (iii) is the least c) fig (ii) is the same as fig (iii) but is smaller than fig (iv) d) is the same for all the figures
The correct option is d) is the same for all the figures
A point positive charge is brought near an isolated conducting sphere. The electric field is best given by a) fig (i) b) fig (ii) c) fig (iii) d) fig (iv)
The correct option is a) fig (i)
A plane EM wave travelling along z-direction is described by 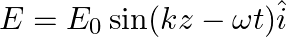 and
and 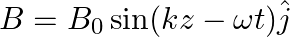 Show that
Show that
i) the average energy density of the wave is given by 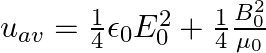
ii) the time-averaged intensity of the wave is given by 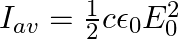
i) The energy density due to electric field $E$ is given as $\mathrm{uE}=1 / 2 \varepsilon_{0} \mathrm{E}^{2}$ The energy density due to magnetic field $B$ is givena as $\mathrm{uB}=1 / 2...
A plane EM wave travelling in vacuum along z-direction is given by 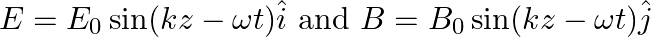
a) Use equation 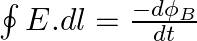 to prove
to prove 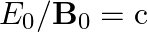
b) by using a similar process and the equation 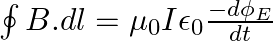 , prove that
, prove that 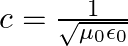
a) Substituting the above equations in the following equation we get ${c} \oint E . d l=-\frac{d \phi_{B}}{d t}=-\frac{d}{d t} \oint B \cdot d s$ So, $E_{0} / B_{0}=0$ b) We get $c=1 /...
A plane EM wave travelling in vacuum along z-direction is given by 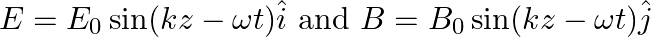
a) evaluate 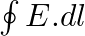 over the rectangular loop 1234 shown in the figure
over the rectangular loop 1234 shown in the figure
b) evaluate 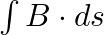 over the surface bounded by loop 1234
over the surface bounded by loop 1234
Solution: (a) $\oint_{\vec{E}} \cdot \overrightarrow{d l}=E_{0} h\left[\sin \left(k z_{2}-\omega t\right)-\sin \left(k z_{1}-\omega t\right)\right]$ (b) $\int \vec{B}.{\overrightarrow{d s}} =...
A long straight cable of length 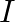 is placed symmetrically along the z-axis and has radius
is placed symmetrically along the z-axis and has radius 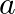 . The cable consists of a thin wire and a co-axial conducting tube. An alternating current
. The cable consists of a thin wire and a co-axial conducting tube. An alternating current 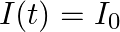 sin
sin 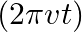 flows down the central thin wire and returns along the co-axial conducting tube. The induced electric field at a distance
flows down the central thin wire and returns along the co-axial conducting tube. The induced electric field at a distance 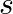 from the wire inside the cable is
from the wire inside the cable is 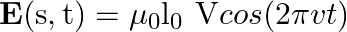 . In
. In 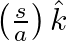 ,
,
compare the conduction current 10 with the displacement current 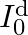
The displacement will be, $I_{0}^{\mathrm{d}} / \mathrm{I}_{0}=(\mathrm{am} / \lambda)^{2}$
A long straight cable of length 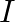 is placed symmetrically along the z-axis and has radius
is placed symmetrically along the z-axis and has radius 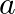 . The cable consists of a thin wire and a co-axial conducting tube. An alternating current
. The cable consists of a thin wire and a co-axial conducting tube. An alternating current 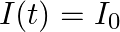 sin
sin 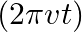 flows down the central thin wire and returns along the co-axial conducting tube. The induced electric field at a distance
flows down the central thin wire and returns along the co-axial conducting tube. The induced electric field at a distance 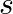 from the wire inside the cable is
from the wire inside the cable is 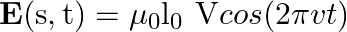 . In
. In 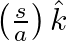 ,
,
a) calculate the displacement current density inside the cable
b) integrate the displacement current density across the cross-section of the cable to find the total displacement current I
a) The displacement current density is given as $\vec{J}_{d}=\frac{2 \pi I_{0}}{\lambda^{2}} \ln \frac{a}{s} \sin 2 \pi v t \hat{k}$ b) Total displacement current will be, $I^{d}=\int J_{d} 2 \pi s...
Seawater at frequency 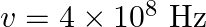 has permittivity
has permittivity 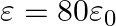 , permeability
, permeability 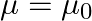 and resistivity
and resistivity 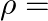
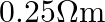 . Imagine a parallel plate capacitor immersed in seawater and driven by an alternating voltage source
. Imagine a parallel plate capacitor immersed in seawater and driven by an alternating voltage source 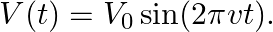 What fraction of the conduction current density is the displacement current density?
What fraction of the conduction current density is the displacement current density?
The separation between the plates of the capacitor is given as $V(t)=V_{0} \sin (2 \pi v t)$ Ohm's law for the conduction of current density is given as $\mathrm{J}_{0}{...
An infinitely long thin wire carrying a uniform linear static charge density 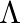 is placed along the z-axis. The wire is set into motion along its length with a uniform velocity
is placed along the z-axis. The wire is set into motion along its length with a uniform velocity 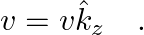 Calculate the pointing vectors
Calculate the pointing vectors 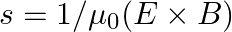
The electric field in an infinitely long thin wire is given by the expression, $\vec{E}=\frac{\lambda \hat{e}_{s}}{2 \pi \epsilon_{0} a} \hat{j}$ Magnetic field due to the wire is given by the...
Even though an electric field E exerts a force qE on a charged particle yet the electric field of an EM wave does not contribute to the radiation pressure. Explain.
Despite the fact that an electric field E imposes a force qE on a charged particle, the electric field of an EM wave has no effect on radiation pressure because radiation pressure is the product of...
What happens to the intensity of light from a bulb if the distance from the bulb is doubled? As a laser beam travels across the length of a room, its intensity essentially remains constant. What geometrical characteristics of the LASER beam is responsible for the constant intensity which is missing in the case of light from the bulb?
When the distance between two points is doubled, the intensity of light is reduced by one-fourth. Geometrical characteristics of the LASER are: a) unidirectional b) monochromatic c) coherent...
Show that the radiation pressure exerted by an EM wave of intensity I on a surface kept in vacuum is I/c.
Energy received by the surface per second is given as $E = IA$ Number of photons received by the surface per second is given as $N$ The perfect absorbing can be expressed as $h/ \lambda$ Hence,...
You are given a 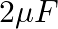 parallel plate capacitor. How would you establish an instantaneous displacement current of
parallel plate capacitor. How would you establish an instantaneous displacement current of 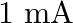 in the space between its plates?
in the space between its plates?
The capacitance of the capacitor is given by $\mathrm{C}=2 \mu \mathrm{F}$ Displacement current is given as $I_{d}=1 \mathrm{~mA}$ Hence, Charge in capacitor will be, $q=C V$ $\mathrm{dV} /...
Show that the average value of radiant flux density S over a single period 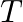 is given by
is given by 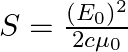
Radiant flux density is given as $\vec{S}=\frac{1}{\mu_{0}}\left(\vec{E} \times \vec B\right)=c^{2} \epsilon_{0}\left({\vec{E}} \times \vec B\right)$ $\mathrm{E}=\mathrm{E}_{0} \cos...
Electromagnetic waves with wavelength
i) 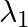 is used in satellite communication
is used in satellite communication
ii) 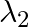 is used to kill germs in water purifies
is used to kill germs in water purifies
iii) 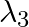 is used to detect leakage of oil in underground pipelines
is used to detect leakage of oil in underground pipelines
iv) 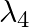 is used to improve visibility in runaways during fog and mist conditions
is used to improve visibility in runaways during fog and mist conditions
a) identify and name the part of the electromagnetic spectrum to which these radiations belong
b) arrange these wavelengths in ascending order of their magnitude
c) write one more application of each
a) i) $\lambda_{1}$ is a microwave, used in satellite communication. ii) $\lambda_{2}$ is UV rays, used in a water purifier for killing germs. iii) $\lambda_{3}$ is X-rays, used in improving the...
The figure shows a standard two-slit arrangement with slits S1, S2. P1, P2 are the two minima points on either side of P. At P2 on the screen, there is a hole and behind P2 is a second 2- slit arrangement with slits S3, S4 and a second screen behind them;(a) There would be no interference pattern on the second screen but it would be lighted (b) The second screen would be totally dark (c) There would be a single bright point on the second screen (d) There would be a regular two-slit pattern on the second screen
The correct answer is d) there would be a regular two-slit pattern on the second screen
Why is the diffraction of sound waves more evident in daily experience than that of lightwave?
Sound waves have a frequency of 20 Hz to 20,000 Hz and a wavelength of 15 m to 15 mm, respectively. When the size of the slit is similar to the wavelength of the sound, it causes diffraction....
The human eye has an approximate angular resolution of φ = 5.8 × 10–4 rad and a typical photo printer prints a minimum of 300 dpi (dots per inch, 1 inch = 2.54 cm). At what minimal distance z should a printed page be held so that one does not see the individual dots.
Angular separation, φ = 5.8 × 10–4 rad The average distance between the two dots = 2.54/300 = 0.85 × 10-2 cm At distance z cm, the angle subtended = 0.85 × 10-2/z Resolution angle for human = 0.85 ×...
A polaroid (I) is placed in front of a monochromatic source. Another polaroid (II) is placed in front of this polaroid (I) and rotated till no light passes. A third polaroid (III) is now placed in between (I) and (II). In this case, will light emerge from (II)? Explain.
A monochromatic source is placed in front of polaroid (I), and polaroid (II) is positioned in front of polaroid (I) (I). The light is unaltered as it travels through the polaroid (II). The Polaroid...
For the same objective, find the ratio of the least separation between two points to be distinguished by a microscope for light of 5000 Ao and electrons accelerated through 100V used as the illuminating substance.
5000 Ao = 5000 × 10-10 m 1/d = 2 sin β/1.22λ dmin = 1.22 λ/ 2 sin β λd = 1.22/10 × 10-10 m When the 100V light is used, d’min = 1.22 λd/ 2 sin β d’min = 1.22 × 1.22 × 10-10/2 sin β The required...
Show that the magnetic field 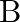 at a point in between the plates of a parallel plate capacitor during charging is
at a point in between the plates of a parallel plate capacitor during charging is 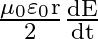
Let $I_{d}$ be the displacement current in the magnetic field region between two parallel plate capacitor plates. The magnetic field induction at a point between two capacitor plates at a...
Consider a two-slit interference arrangements such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen falls at a distance D from the centre O.
The minima will occur when ∆x = S2P – S1P = (2n-1/2)λ S1P = √D2 + (D – x)2 S2P = √D2 + (D + x)2 T2P = D + x T1P = D – x [D2 + (D+x)2]-1/2 – [D2+(D-x)2]1/2 = λ/2 D =...
Four identical monochromatic sources A, B, C, D as shown in the figure produce waves of the same wavelength λ and are coherent. Two receiver R1 and R2 are at great but equal distances from B. (i) Which of the two receivers picks up the larger signal? (ii) Which of the two receivers picks up the larger signal when B is turned off? (iii) Which of the two receivers picks up the larger signal when D is turned off? (iv) Which of the two receivers can distinguish which of the sources B or D has been turned off?
i) R2 is the larger signal. ii) When B is switched off, R1 is y = a cos ꞷt IR1 = a2/2 R2 is y = a cos ꞷt IR2 = a2/2 So, it can be said that R1 and R2 are the same. iii) When D is switched off, R1 is...
The optical properties of a medium are governed by the relative permittivity (εr) and relative permeability (µr ). The refractive index is defined as √µr εr = n. For ordinary material εr > 0 and µr > 0 and the positive sign is taken for the square root. In 1964, a Russian scientist V. Veselago postulated the existence of material with εr < 0 and µr < 0. Since then such ‘metamaterials’ have been produced in the laboratories and their optical properties studied. For such materials n = -√µrεr. As light enters a medium of such refractive index the phases travel away from the direction of propagation. (i) According to the description above show that if rays of light enter such a medium from the air (refractive index =1) at an angle θ in 2nd quadrant, them the refracted beam is in the 3rd quadrant (ii) Prove that Snell’s law holds for such a medium
BC = √μrεr (CD-AE) BC >0; CD > AE -√μrεr AE = BC – √μrεr CD BC = √μrεr (CD – AE) AE > CD Therefore, BC < 0 ii) BC = AC sin θi CD – AE = AC sin θr BC = √μrεr AC sin θi = √μrεr AC sin θr...
Professor C.V.Raman surprised his students by suspending freely a ting light ball in a transparent vacuum chamber by shining a laser beam on it. Which property of EM waves was he exhibiting? Give one more example of this property.
Professor CV Raman demonstrated the radiation pressure property of EM waves.
To ensure almost 100 per cent transmissivity, photographic lenses are often coated with a thin layer of dielectric material. The refractive index of this material is intermediated between that of air and glass (which makes the optical element of the lens). A typically used dielectric film is MgF2 (n = 1.38). What should the thickness of the film be so that at the centre of the visible spectrum (5500 Ao) there is maximum transmission?
IA is incident at point A, forming an incident angle I between the air and the film surface. The reflected and refracted rays are AR1 and AD, respectively. D is the point where the partial...
Poynting vectors 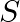 is defined as a vector whose magnitude is equal to the wave intensity and whose direction is along the direction of wave propagation. Mathematically, it is given by
is defined as a vector whose magnitude is equal to the wave intensity and whose direction is along the direction of wave propagation. Mathematically, it is given by 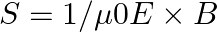 . Show that nature of
. Show that nature of 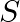 versus
versus 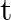 graph.
graph.
The magnetic field of a beam emerging from a filter facing a floodlight is given by 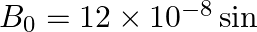
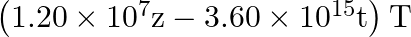 . What is the average intensity of the beam?
. What is the average intensity of the beam?
$\begin{array}{l} B_{0}=12 \times 10^{-8} \sin \left(1.20 \times 10^{7} z-3.60 \times 10^{15} \mathrm{t}\right) \mathrm{T} \\ \mathrm{B} 0=12 \times 10^{-8} \mathrm{~T} \\ \mathrm{lav}=1.71...
Consider a 20 W bulb emitting light of wavelength 5000 A ° and shining on a metal surface kept at a distance 2m. Assume that the metal surface has work function of 2 eV and that each atom on the metal surface can be treated as a circular disk of radius 1.5 A ° . (i) Estimate no. of photons emitted by the bulb per second. [Assume no other losses] (ii) Will there be photoelectric emission? (iii) How much time would be required by the atomic disk to receive energy equal to work function (2 eV)? (iv) How many photons would atomic disk receive within time duration calculated in (iii) above? (v) Can you explain how photoelectric effect was observed instantaneously?
Given, P = 20W λ = 5000 Ao = 5000 × 10-10 m d = 2m ϕ0 = 2 eV r = 1.5 × 10-10 m No.of photon emitted per second by the bulb = n’ = dN/dt i) No.of photon emitted by bulb per second = n’ = p λ/hc = 5 ×...
A variable frequency a.c source is connected to a capacitor. How will the displacement current change with a decrease in frequency?
Capacitive reaction is given as, $\mathrm{Xc}=1 / 2 \mathrm{mf} \mathrm{C}$ As the frequency decreases, $X_ c$ rises, and the conduction current becomes inversely proportional to $X_ c$.
A particle A with a mass mA is moving with a velocity v and hits a particle B (mass mB) at rest (one dimensional motion). Find the change in the de Broglie wavelength of the particle A. Treat the collision as elastic.
According to the law of conservation of momentum, mAv + mB0 = mAv1 + mBv2 mA(v-v1) = mBv2 1/2 mAv2 = 1/2 mAv12 + 1/2mBv22 mA(v-v1)(v+v1) = mBv22 v1 = (mA-mB/mA+mB)v v2 = (2mA/mA+mB)v λinitial =...
A student performs an experiment on the photoelectric effect, using two materials A and B. A plot of Vstop vs ν is given in the figure. (i) Which material A or B has a higher work function? (ii) Given the electric charge of an electron = 1.6 × 10–19 C, find the value of h obtained from the experiment for both A and B. Comment on whether it is consistent with Einstein’s theory
i) The threshold frequency of A is vOA = 5 × 1014 Hz The threshold frequency of B is vOB = 10 × 1014 Hz Work function is ϕ = hv0 ϕOA/ ϕOB = 5 × 1014/10 × 1014 < 1 ϕOA <...
The charge on a parallel plate capacitor varies as 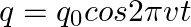 . The plates are very large and close together. Neglecting the edge effects, find the displacement current through the capacitor?
. The plates are very large and close together. Neglecting the edge effects, find the displacement current through the capacitor?
Displacement current through the capacitor is given as, $\mathrm{Id}=\mathrm{Ic}=\mathrm{dq} / \mathrm{dt}$ Given, $q=q_{0} \cos 2 \pi v t$ On putting the values, we get $\mathrm{Id}=\mathrm{Ic}=-2...
Consider an electron in front of the metallic surface at a distance d (treated as an infinite plane surface). Assume the force of attraction by the plate is given as 2 2 0 1 4 4 q πε d Calculate work in taking the charge to an infinite distance from the plate. Taking d = 0.1nm, find the work done in electron volts. [Such a force law is not valid for d < 0.1nm].
An electron is progressively moved in the picture. The distance travelled by the electron is x, and this is accomplished by the application of an external force. F = q2/4×4πε0d2 d = 0.1 nm = 10-10 m...
Consider a thin target ( m square,
m square,  m thickness) of sodium, which produces a photocurrent of 100µA when a light of intensity 100W/m2 (λ = 660nm) falls on it. Find the probability that a photoelectron is produced when a photon strikes a sodium atom. [Take density of Na = 0.97 kg/m3].
m thickness) of sodium, which produces a photocurrent of 100µA when a light of intensity 100W/m2 (λ = 660nm) falls on it. Find the probability that a photoelectron is produced when a photon strikes a sodium atom. [Take density of Na = 0.97 kg/m3].
Area = 10-4 m2 Thickness = 10-3 m Current = 10-4 A Intensity = 100 W/m2 Mass = (volume)(density) = 0.97 × 10-4 gm No.of target atoms = 0.254 × 1019 Total energy = nhv Where n = 3.3 × 1016 The...
Why does a microwave oven heats up a food item containing water molecules most efficiently?
Because the microwave's frequency and the resonant frequency of the water molecules are the same, the microwave oven cooks a food item containing water molecules most efficiently.
A neutron beam of energy E scatters from atoms on a surface with a spacing d = 0.1nm. The first maximum of intensity in the reflected beam occurs at θ = 30°. What is the kinetic energy E of the beam in eV?
From Bragg’s law, 2d sin θ = nλ p = h/λ = 6.6 × 10-24 kg m/s E = 1/2 mv2 = p2/2m E = 0.085 eV
Why is the orientation of the portable radio with respect to broadcasting station important?
As electromagnetic waves are plane polarised, the antenna must be parallel to the vibration of the fields of the wave. The orientation of the portable radio with respect to the transmitting station...
Two particles A and B of de Broglie wavelengths λ1 and λ2 combine to form a particle C. The process conserves momentum. Find the de Broglie wavelength of the particle C. (The motion is one dimensional).
By de-Broglie wavelengths, λ=h/p p=h/ λ p1 = h/ λ1 p2 = h/ λ2 p3 = h/ λ3 There are 4 possible cases and they are: Case 1: When p1 and p2 are positive, then λ3 = λ1 λ1/ λ1+ λ2 Case 2: When p1 and p2...
Two monochromatic beams A and B of equal intensity I, hit a screen. The number of photons hitting the screen by beam A is twice that by beam B. Then what inference can you make about their frequencies?
Let nA represent the number of photons that fall per second from beam A, and nB represent the number of photons that fall per second from beam B. Given, A has twice as many photons reaching the...
Assuming an electron is confined to a 1nm wide region, find the uncertainty in momentum using the Heisenberg Uncertainty principle. You can assume the uncertainty in position ∆x as 1nm. Assuming p = ∆p, find the energy of the electron in electron volts.
As the electrons rotate in a circular path, ∆r = 1 nm = 10-9 m ∆p = h/∆x ∆p = (331/314) × 10-25 E = 1/2 mv2 = ∆p2/2m E = 3.8 × 10-2 eV
An EM wave of intensity I falls on a surface kept in vacuum and exerts radiation pressure 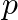 on it. Which of the following are true?
on it. Which of the following are true?
a) radiation pressure is 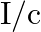 if the wave is totally absorbed
if the wave is totally absorbed
b) radiation pressure is 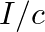 if the wave is totally reflected
if the wave is totally reflected
c) radiation pressure is 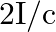 if the wave is totally reflected
if the wave is totally reflected
d) radiation pressure is in the range 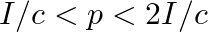 for real surface
for real surface
The correct options are: a) radiation pressure is $\mathrm{l} / \mathrm{c}$ if the wave is totally absorbed c) radiation pressure is $2 \mathrm{l} / \mathrm{c}$ if the wave is totally reflected d)...
Consider a metal exposed to light of wavelength 600 nm. The maximum energy of the electron doubles when light of wavelength 400 nm is used. Find the work function in eV.
Let K1 and K2 be the maximum energy emitted by the electrons when 600 and 400 nm wavelength is used. K2 = 2K1 Therefore, the work function, ϕ = 1.03 eV
Consider the figure given for photoemission. How would you reconcile with momentum-conservation? Note light (photons) have momentum in a different direction than the emitted electrons.
When photons collide with a metal surface, momentum is transferred to the atoms on the metal surface, resulting in a reduction in photon speed. Photons transmit their momentum to the nucleus and...
The source of electromagnetic waves can be a charge
a) moving with a constant velocity
b) moving in a circular orbit
c) at rest
d) falling in an electric field
The correct options are: b) moving in a circular orbit d) falling in an electric field
There are two sources of light, each emitting with a power of 100 W. One emits X-rays of wavelength 1nm and the other visible light at 500 nm. Find the ratio of a number of photons of X-rays to the photons of visible light of the given wavelength?
Ex = hvx Ev = hvv Let nx and nv be the no.of photons from x-rays and visible light are of equal energies and they emit 100 W power. nxhvx = nvhvv nx/nv = vv/vx = λx/λv nx/nv = 1 nm/500 nm nx:nv =...
Do all the electrons that absorb a photon come out as photoelectrons?
No, not every electron absorbed as a photon emerges as a photoelectron.
A charged particle oscillates about its mean equilibrium position with a frequency of 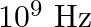 . The electromagnetic waves produced:
. The electromagnetic waves produced:
a) will have a frequency of 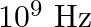
b) will have a frequency of 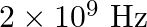
c) will have a wavelength of 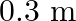
d) fall in the region of radiowaves
The correct options are: a) will have a frequency of $10^{9} \mathrm{~Hz}$ c) will have a wavelength of $0.3 \mathrm{~m}$ d) fall in the region of radiowaves
A proton and an α-particle are accelerated, using the same potential difference. How are the de Broglie wavelengths λp and λa related to each other?
The proton and α-particle are accelerated at the same potential difference. λ = h/√2mqv λ is proportional to 1/√mq λp/ λa = √maqa/mpqp = √8 Hence, proton wavelength is √8 times α-particle....
A particle moves in a closed orbit around the origin, due to a force which is directed towards the origin. The de Broglie wavelength of the particle varies cyclically between two values λ1, λ2 with λ1>λ2. Which of the following statement are true? (a) The particle could be moving in a circular orbit with origin as centre (b) The particle could be moving in an elliptic orbit with origin as its focus (c) When the de Broglie wavelength is λ1, the particle is nearer the origin than when its value is λ2 (d) When the de Broglie wavelength is λ2, the particle is nearer the origin than when its value is λ1
The correct answers are b) The particle could be moving in an elliptic orbit with origin as its focus d) When the de Broglie wavelength is λ2, the particle is nearer the origin than when its value...
Photons absorbed in matter are converted to heat. A source emitting n photon/sec of frequency ν is used to convert 1kg of ice at 0°C to water at 0°C. Then, the time T taken for the conversion (a) decreases with increasing n, with ν fixed (b) decreases with n fixed, ν increasing (c) remains constant with n and ν changing such that nν = constant (d) increases when the product nν increases
The correct answers are a) decreases with increasing n, with ν fixed b) decreases with n fixed, ν increasing c) remains constant with n and ν changing such that nν = constant
The de Broglie wavelength of a photon is twice the de Broglie wavelength of an electron. The speed of the electron is ve = c/100. Then (a)  (b)
(b) (c)
(c)  (d)
(d) 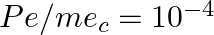
The correct answers are b) Ee/Ep = 10-2 c) Pe/mec = 10-2
Two particles A1 and A2 of masses m1, m2 (m1 > m2) have the same de Broglie wavelength. Then (a) their momenta are the same (b) their energies are the same (c) energy of A1 is less than the energy of A2 (d) energy of A1 is more than the energy of A2
The correct answers are a) their momenta are the same c) energy of A1 is less than the energy of A2
Relativistic corrections become necessary when the expression for the kinetic energy 1/2 mv2 , becomes comparable with mc2, where m is the mass of the particle. At what de Broglie wavelength will relativistic corrections become important for an electron? (a) λ =10nm (b) nm (c)
nm (c)  nm (d)
nm (d) nm
nm
The correct answers are c) λ =10–4nm d) λ =10–6nm
An electron is moving with an initial velocity  and is in a magnetic field
and is in a magnetic field 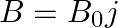 Then it’s de Broglie wavelength (a) remains constant (b) increases with time (c) decreases with time (d) increases and decreases periodically
Then it’s de Broglie wavelength (a) remains constant (b) increases with time (c) decreases with time (d) increases and decreases periodically
The correct answer is a) remains constant
A proton, a neutron, an electron and an α-particle have the same energy. Then their de Broglie wavelengths compare as (a) λp = λn > λe > λα (b) λα < λp = λn < λe (c) λe < λp = λn > λα (d) λe = λp = λn = λα
The correct answer is b) λα < λp = λn < λe
A particle is dropped from a height H. The de Broglie wavelength of the particle as a function of height is proportional to (a) H (b) H ½ (c) H0 (d)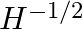
The correct answer is d) H–1/2
A plane electromagnetic wave propagating along  -direction can have the following pairs of
-direction can have the following pairs of  and
and 
a) 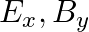
b) 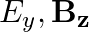
c) 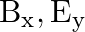
d) 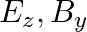
The correct options are: b) $E_y, \mathbf{B_ z}$ d) $E_z, B_y$
An electromagnetic wave travelling along the 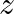 -axis is given as:
-axis is given as: 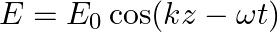 . Choose the correct options from the following a) the associated magnetic field is given as
. Choose the correct options from the following a) the associated magnetic field is given as 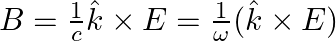
b) the electromagnetic field can be written in terms of the associated magnetic field as
c)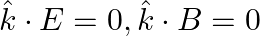
d)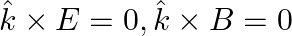
a) the associated magnetic field is given as $B=\frac{1}{c} \hat{k} \times E=\frac{1}{\omega}(\hat{k} \times E)$ b) the electromagnetic field can be written in terms of the associated magnetic field...
An electromagnetic wave travels in vacuum along z-direction: 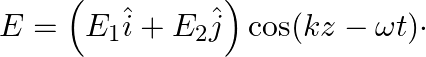 Choose the correct options from the following:
Choose the correct options from the following:
a) the associated magnetic field is given as 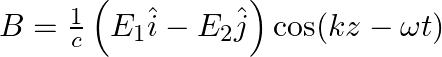
b) the associated magnetic field is given as 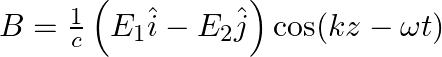
c) the given electromagnetic field is circularly polarised
d) the given electromagnetic waves is plane polarised
a) the associated magnetic field is given as $B=\frac{1}{c}\left(E_{1} \hat{i}-E_{2} \hat{j}\right) \cos (k z-\omega t)$ d) the given electromagnetic waves is plane polarised
An EM wave radiates outwards from a dipole antenna, with  as the amplitude of its electric field vector. The electric field
as the amplitude of its electric field vector. The electric field  which transports significant energy from the source falls off as
which transports significant energy from the source falls off as
a) 
b) 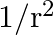
c) 
d) remains constant
c) $1 / \mathrm{r}$
The ratio of contributions made by the electric field and magnetic field components to the intensity of an EM wave is
a) 
b) 
c) 
d) 
c) $1: 1$
If  and
and  represent electric and magnetic field vectors of the electromagnetic wave, the direction of propagation of the electromagnetic wave is along
represent electric and magnetic field vectors of the electromagnetic wave, the direction of propagation of the electromagnetic wave is along
a) 
b) 
c) 
d) 
d) $E \times B$
The electric field intensity produced by the radiations coming from 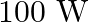 bulb at a
bulb at a 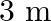 distance is E. The electric field intensity produced by the radiations coming from
distance is E. The electric field intensity produced by the radiations coming from 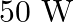 bulb at the same distance is
bulb at the same distance is
a) 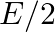
b) 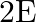
c) 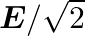
d) 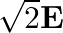
c) $\mathrm{E} / \sqrt{2}$
Light with an energy flux of 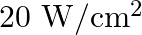 falls on a non-reflecting surface at normal incidence. If the surface has an area of
falls on a non-reflecting surface at normal incidence. If the surface has an area of  , the total momentum delivered during 30 minutes is
, the total momentum delivered during 30 minutes is
a) 
b) 
c) 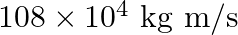
d) 
b) $36 \times 10^{-4} \mathrm{~kg} \mathrm{~m} / \mathrm{s}$
A linearly polarized electromagnetic wave given as 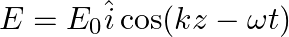 is incident normally on a perfectly reflecting infinite wall at
is incident normally on a perfectly reflecting infinite wall at  .
.
Assuming that the material of the wall is optically inactive, the reflected wave will be given as
a)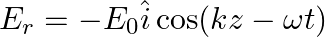
b)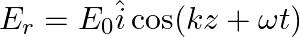
c)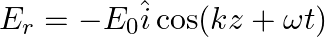
d)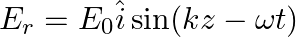
b)$E_{r}=E_{0} \hat{i} \cos (k z+\omega t)$
In the LCR circuit the ac driving voltage is v = vm sin ωt.
Describe subsequent motion of charges.
R must be short-circuited in order for the circuit to become an LC oscillator. The capacitor will continue to drain, and all of the energy will be transferred to L and back. Energy will oscillate...
In the LCR circuit the ac driving voltage is v = vm sin ωt.
(i) Write down the equation of motion for q (t).
(ii) At  , the voltage source stops and R is short-circuited. Now write down how much energy is stored in each of L and C.
, the voltage source stops and R is short-circuited. Now write down how much energy is stored in each of L and C.
i) The equation for charge motion variation with respect to time is as follows: $\mathrm{L} d^{2} q(\mathrm{t}) / \mathrm{dt}+\mathrm{R} \mathrm{dq}(\mathrm{t}) / \mathrm{dt}+\mathrm{q}(\mathrm{t})...
For an LCR circuit driven at frequency ω, the equation reads L di/dt + Ri + q/C = vi = vm sin ꞷ t
(i) Cast the equation in the form of a conservation of energy statement
(ii) Integrate the equation over one cycle to find that the phase difference between v and i must be acute.
i) The first equation is in the form of conservation of energy ii) We get dt as positive when we integrate the equation from $0$ to $T$, which is possible when the phase difference is constant and...
For an LCR circuit driven at frequency ω, the equation reads L di/dt + Ri + q/C = vi = vm sin ꞷ t
(i) Multiply the equation by i and simplify where possible.
(ii) Interpret each term physically.
Given equation is, $L d i / d t+R i+q / C=v i=v m \sin \omega t$ i) On multiplying the above equation with I, we get, $\mathrm{d}\left(1 / 2 \mathrm{Li}^{2}\right) / \mathrm{dt}+1 / 2 \mathrm{C}...
Consider the LCR circuit such that the net current i and the phase of i. Show that i = V/Z . Find the impedance Z for this circuit.
The impedance $Z$ for the given circuit is represented as, $1 / \mathrm{Z}=\left[1 / \mathrm{R}^{2}+1 /(1 / \omega \mathrm{C}-\omega \mathrm{L})^{2}\right]^{1 / 2}$
1MW power is to be delivered from a power station to a town 10 km away. One uses a pair of Cu wires of radius 0.5 cm for this purpose. Calculate the fraction of ohmic losses to power transmitted if
(i) power is transmitted at 220V. Comment on the feasibility of doing this.
(ii) a step-up transformer is used to boost the voltage to 11000 V, power transmitted, then a step-down transformer is used to bring the voltage to 220 V.
i) It is given that the power station is $10 \mathrm{~km}$ away from the town Length of the $\mathrm{Cu}$ wire is given as $\mathrm{L}=20 \mathrm{~km}=20000 \mathrm{~m}$ Resistance of $\mathrm{Cu}$...
An electrical device draws 2kW power from AC mains (voltage 223V (rms) = 50,000 V). The current differs (lags) in phase by φ (tan φ = -3/4) as compared to voltage.
Find (i) R,
(ii)  ,
,
and (iii) 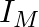 . Another device has twice the values for
. Another device has twice the values for 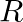 ,
, 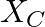 and
and 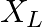 . How are the answers affected?
. How are the answers affected?
Impedance is given as Z = 25 ohms $635=25R^{2}/16$ a) Resistance can be calculated as, $R=\sqrt 25\times 16=\sqrt 400=20 ohms$ b) $X_{c}-X_{l}=-3R/4=-15ohms$ c) Main current will be...
Explain why the reactance offered by an inductor increases with increasing frequency of an alternating voltage.
The reactance offered by an inductor increases with the increasing frequency of an alternating voltage because the induced emf is proportional to the rate of change of current.
Explain why the reactance provided by a capacitor to an alternating current decreases with increasing frequency.
Because capacitance reactance is inversely proportional to frequency, and capacitors have a tendency to pass high-frequency current while blocking low-frequency currents, the reactance delivered by...
A 60 W load is connected to the secondary of a transformer whose primary draws line voltage. If a current of 0.54 A flows in the load, what is the current in the primary coil? Comment on the type of transformer being used.
$P_{s}$ is given as $60W$ $I_{s}$ is given as $0.54A$ Primary voltage is given as $220V$ $V_{s}=60/0.54=110V$ The transformer is a step-down transformer because the secondary voltage is lower than...
A coil of 0.01-henry inductance and 1-ohm resistance is connected to 200 volt, 50 Hz ac supply. Find the impedance of the circuit and time lag between max. alternating voltage and current.
Inductance L is given as 0.01 H Resistance R is given as 1 ohm Voltage is given as 200 V Frequency is given as 50 Hz Impedance is given Z = 3.3 ohms Phase difference will be 72 × π/180 rad 0.004 sec...
Both alternating current and direct current are measured in amperes. But how is the ampere defined for an alternating current?
The phenomenon called Joule's law of heating is used to determine the ampere for an alternating current. According to Joule's law of heating in a one-ohm resistance, AC is the current produced in a...
A device ‘X’ is connected to an a.c source. The variation of voltage, current and power in one complete cycle is shown in the figure.
Identify the device ‘X’.
Solution: X could be an inductor, a capacitor, or a hybrid of the two.
A device ‘X’ is connected to an a.c source. The variation of voltage, current and power in one complete cycle is shown in the figure.
(a) Which curve shows power consumption over a full cycle?
(b) What is the average power consumption over a cycle?
Solution: a) The greatest amplitude of the power curve is equal to the product of the voltage and current amplitudes. As a result, curve A denotes power. b) Because the whole cycle in the graph...
How does the sign of the phase angle φ, by which the supply voltage leads the current in an LCR series circuit, change as the supply frequency is gradually increased from very low to very high values.
$tan \phi = \frac{X_{l}-X_{c}}{R}$ $X_{l}<X_{c}$ At resonate frequency we have, $X_{l}=X_{c}$ $tan \phi = 0$
The alternating current in a circuit is described by the graph shown in the figure. Show rms current in this graph.
Solution: $I_{rms}=1.6A$
In series LCR circuit, the plot of I max vs ω is shown in the figure. Find the bandwidth and mark in the figure.
Frequency 1 is 0.8 rad/s Frequency 2 is 1.2 rad/s The bandwidth is 0.4 rad/s
Can the instantaneous power output of an ac source ever be negative? Can the average power output be negative?
a) When P < 0, then AC source's instantaneous power output can be negative. b) The average power output cannot be negative as $P_{av}>0$.
Study the circuits (a) and (b) shown in the figure and answer the following questions.
(a) Under which conditions would the rms currents in the two circuits be the same? (b) Can the rms current in the circuit (b) be larger than that in (a)? Solution: a) $(I_{rms})a=(I_{rms})b$...
Draw the effective equivalent circuit of the circuit shown in the figure, at very high frequencies and find the effective impedance.
Solution: The effective impedance will be, $Z_{eq}=R_{1}+R_{3}$
If an LC circuit is considered analogous to a harmonically oscillating spring block system, which energy of the LC circuit would be analogous to potential energy and which one analogous to kinetic energy?
The magnetic energy of the LC circuit is equivalent to kinetic energy, while electrostatic energy due to a capacitor's charge change is analogous to potential energy.
The line that draws power supply to your house from street has
(a) zero average current.
(b) 220 V average voltage.
(c) voltage and current out of phase by 90°.
(d) voltage and current possibly differing in phase φ such that |φ| < π/2.
The correct options are: (a) zero average current. (d) voltage and current possibly differing in phase φ such that |φ| < π/2.
When an AC voltage of 220 V is applied to the capacitor C
(a) the maximum voltage between plates is 220 V.
(b) the current is in phase with the applied voltage.
(c) the charge on the plates is in phase with the applied voltage.
(d) power delivered to the capacitor is zero.
The correct options are: (c) the charge on the plates is in phase with the applied voltage. (d) power delivered to the capacitor is zero.
For an LCR circuit, the power transferred from the driving source to the driven oscillator is P = I2Z cos φ.
(a) Here, the power factor cos 0, 0. φ ≥ ≥ P
(b) The driving force can give no energy to the oscillator (P = 0) in some cases.
(c) The driving force cannot syphon out (P < 0) the energy out of oscillator.
(d) The driving force can take away energy out of the oscillator.
The correct options are: (a) Here, the power factor cos 0, 0. φ ≥ ≥ P (b) The driving force can give no energy to the oscillator (P = 0) in some cases. (c) The driving force cannot syphon out (P...
