Chloride radical is detected by the chromyl chloride test. In this test, chromyl chloride gas (orange red color) is produced. Equation Involved – 4NaCl + K2Cr2O7 + 6H2SO4 → 4NaHSO4 + 2KHSO4 + 3H2O +...
CBSE Study Material
What do you understand by lanthanide contraction
The lanthanide contraction is the decrease in the atomic or ionic radii with increase in the atomic number of lanthanides
What are lanthanide elements?
Lanthanide elements resembles a lot in properties with lanthanum. Lanthanide is group of 14 elements from atomic number 58 to 71. In these elements on increasing atomic number electron enters into...
Explain oxidization properties of potassium permanganate in acidic medium.
2KMnO4 + 8H2SO4 + 10KI → 6K2SO4 + 8H2O + 5I2 2KMnO4 + 5SO2 + 2H2O → 2MnSO4 + 2H2SO4 + K2SO4 2KmO4 + 16HCl → 2KCl + 2MnCl2 + 8H2O + 5Cl2 5COOH – COOH + [5O] → 10CO2 + 5H2O
Show that the lines
Compute the shortest distance between the lines
Find the shortest distance between the given lines.
Find the shortest distance between the given lines.
Find the shortest distance between the given lines.
Find the shortest distance between the given lines.
Find the shortest distance between the given lines.
Find the shortest distance between the given lines.
Find the shortest distance between the given lines.
Give two differences between double salt and complex salt.
Answer: Double salt Complex salt A double salt is a combination of two salt compounds. A complex salt is a molecular structure that is composed of one or more complex ions. Double salts can give...
Give two differences between DNA and RNA.
Answer: DNA RNA DNA – Deoxyribo Nucleic Acid RNA – Ribo Nucleic acid DNA consists of adenine (A), cytosine (C), guanine (G), and thymine (T) RNA consists of adenine (A), cytosine (C), guanine (G),...
Find the shortest distance between the given lines. ![Rendered by QuickLaTeX.com \[\begin{array}{l} \square \vec{r}=(\hat{i}+\hat{j})+\lambda(2 \hat{i}-\hat{j}+\hat{k}) \\ \vec{r}=(2 \hat{i}+\hat{j}-\hat{k})+\mu(3 \hat{i}-5 \hat{j}+2 \hat{k}) \end{array}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2f8ab5b81e582387cb9ae472791476e4_l3.png)
![Rendered by QuickLaTeX.com \[\begin{array}{l} \square \vec{r}=(\hat{i}+\hat{j})+\lambda(2 \hat{i}-\hat{j}+\hat{k}) \\ \vec{r}=(2 \hat{i}+\hat{j}-\hat{k})+\mu(3 \hat{i}-5 \hat{j}+2 \hat{k}) \end{array}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2f8ab5b81e582387cb9ae472791476e4_l3.png)
Answer Given equations: r¯=(ı^+ȷ^)+λ(2ı^-ȷ^+k^) \overline{\mathrm{r}}=(\hat{\imath}+\hat{\jmath})+\lambda(2 \hat{\imath}-\hat{\jmath}+\hat{\mathrm{k}})...
Find the shortest distance between the given lines. ![Rendered by QuickLaTeX.com \[\begin{array}{l} \square \vec{r}=(\hat{i}+\hat{j})+\lambda(2 \hat{i}-\hat{j}+\hat{k}) \\ \vec{r}=(2 \hat{i}+\hat{j}-\hat{k})+\mu(3 \hat{i}-5 \hat{j}+2 \hat{k}) \end{array}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2f8ab5b81e582387cb9ae472791476e4_l3.png)
![Rendered by QuickLaTeX.com \[\begin{array}{l} \square \vec{r}=(\hat{i}+\hat{j})+\lambda(2 \hat{i}-\hat{j}+\hat{k}) \\ \vec{r}=(2 \hat{i}+\hat{j}-\hat{k})+\mu(3 \hat{i}-5 \hat{j}+2 \hat{k}) \end{array}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2f8ab5b81e582387cb9ae472791476e4_l3.png)
Answer Given equations: r¯=(ı^+ȷ^)+λ(2ı^-ȷ^+k^) \overline{\mathrm{r}}=(\hat{\imath}+\hat{\jmath})+\lambda(2 \hat{\imath}-\hat{\jmath}+\hat{\mathrm{k}})...
Which of the following compounds has tetrahedral geometry? (a) ![Rendered by QuickLaTeX.com \left[\mathrm{Ni}(\mathrm{CN})_{4}\right]^{-2}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c5a91864ba7e1e0ed1b5d273d822f5e5_l3.png) (b)
(b) ![Rendered by QuickLaTeX.com \left[\mathrm{Pd}(\mathrm{CN})_{4}\right]^{2-}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-ffda616d3dbe7dc8925722e87005924e_l3.png) (c)
(c) ![Rendered by QuickLaTeX.com \left[\mathrm{PdCl}_{4}\right]^{2-}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-90cc6a4f4d42dee46e06d6f8ed516b7a_l3.png) (d)
(d) ![Rendered by QuickLaTeX.com \left[\mathrm{NiCl}_{4}\right]^{2}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-149ee5c95bd9cfcc4405704fba2e1bab_l3.png)
SOL: Correct option is D. $\left[\mathrm{NiCl}_{4}\right]^{2}$
Oxidation number of gold metal is (a)+1 (b) 0 (c) 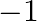 (d) all of these
(d) all of these
Sol: Correct option is B. 0
If A(1, 2, 3), B(4, 5, 7), C(-4, 3, -6) and D(2, 9, 2) are four given points then find the angle between the lines AB and CD.
Answer Given - A = (1,2,3) B = (4,5,7) C = (-4,3,-6) D = (2,9,2) Formula to be used – If P = (a,b,c) and Q = (a’,b’,c’),then the direction ratios of the line PQ is given by ((a’-a),(b’-b),(c’-c))...
Show that the lines x = – y = 2z and x + 2 = 2y – 1 = – z + 1 are perpendicular to each other.
To prove – The lines are perpendicular to each other Direction ratios of L1 = (2,-2,1) Direction ratios of L2 = (2,1,-2) Tip – If (a,b,c) be the direction ratios of the first line and (a’,b’,c’) be...
prove that
To find – The value of λ Direction ratios of L1 = (-3,2λ,2) Direction ratios of L2 = (3λ,1,-5) Tip – If (a,b,c) be the direction ratios of the first line and (a’,b’,c’) be that of the second, then...
To prove – The lines are perpendicular to each other Direction ratios of L1 = (2,-3,4) Direction ratios of L2 = (2,4,2) Tip – If (a,b,c) be the direction ratios of the first line and (a’,b’,c’) be...
Find the angle between each of the following pairs of lines:
To find – Angle between the two pair of lines Direction ratios of L1 = (-3,-2,0) Direction ratios of L2 = (1,-3,2) Tip – If (a,b,c) be the direction ratios of the first line and (a’,b’,c’) be that...
Find the angle between each of the following pairs of lines:
To find – Angle between the two pair of lines Direction ratios of L1 = (1,0,-1) Direction ratios of L2 = (3,4,5) Tip – If (a,b,c) be the direction ratios of the first line and (a’,b’,c’) be that of...
Find the angle between each of the following pairs of lines:
To find – Angle between the two pair of lines Direction ratios of L1 = (2,1,-3) Direction ratios of L2 = (3,2,-1) Tip – If (a,b,c) be the direction ratios of the first line and (a’,b’,c’) be that of...
Find the angle between each of the following pairs of lines:
To find – Angle between the two pair of lines Direction ratios of L1 = (4,3,5) Direction ratios of L2 = (1,-1,1) Tip – If (a,b,c) be the direction ratios of the first line and (a’,b’,c’) be that of...
Find the angle between each of the following pairs of lines
To find – Angle between the two pair of lines Direction ratios of L1 = (1,1,2) Direction ratios of L2 = (3,5,4) Tip – If (a,b,c) be the direction ratios of the first line and (a’,b’,c’) be that of...
Find the angle between each of the following pairs of lines:
To find – Angle between the two pair of lines Direction ratios of L1 = (2,-2,1) Direction ratios of L2 = (1,2,-2) Tip – If (a,b,c) be the direction ratios of the first line and (a’,b’,c’) be that of...
Find the angle between each of the following pairs of lines
Tip – If (a,b,c) be the direction ratios of the first line and (a’,b’,c’) be that of the second, then the angle between these pair of lines is given by
The position vectors of three points A, B and C are
It can thus be written as: A = (-4,2,-3) B = (1,3,-2) C = (-9,1,-4) To prove – A, B and C are collinear Formula to be used – If P = (a,b,c) and Q = (a’,b’,c’),then the direction ratios of the line...
Find the values of λ and μ so that the points A(-1, 4, -2), B(λ, μ 1) and C(0, 2, -1) are collinear.
Answer Given - A = (-1,4,-2) B = (λ,μ,1) C = (0,2,-1) To find – The value of λ and μ so that A, B and C are collinear Formula to be used – If P = (a,b,c) and Q = (a’,b’,c’),then the direction ratios...
Find the values of λ and μ so that the points A(3, 2, -4), B(9, 8, -10) and C(λ, μ -6) are collinear.
Answer Given - A = (3,2,-4) B = (9,8,-10) C = (λ,μ,-6) To find – The value of λ and μ so that A, B and C are collinear Formula to be used – If P = (a,b,c) and Q = (a’,b’,c’),then the direction...
Find the value of λ for which the points A(2, 5, 1), B(1, 2, -1) and C(3, λ, 3) are collinear.
Answer Given - A = (2,5,1) B = (1,2,-1) C = (3,λ,3) To find – The value of λ so that A, B and C are collinear Formula to be used – If P = (a,b,c) and Q = (a’,b’,c’),then the direction ratios of the...
Show that the points A(2, 3, -4), B(1, -2, 3) and C(3, 8, -11) are collinear.
Answer Given - A = (2,3,-4) B = (1,-2,3) C = (3,8,-11) To prove – A, B and C are collinear Formula to be used – If P = (a,b,c) and Q = (a’,b’,c’),then the direction ratios of the line PQ is given by...
Show that the points A(2, 1, 3), B(5, 0, 5) and C(-4, 3, -1) are collinear.
Answer Given - A = (2,1,3) B = (5,0,5) C = (-4,3,-1) To prove – A, B and C are collinear Formula to be used – If P = (a,b,c) and Q = (a’,b’,c’),then the direction ratios of the line PQ is given by...
Find the image of the point (2, -1, 5) in the line
Find the image of the point $(2,-1,5)$ in the line r→=(11i^-2j^-8k^)+λ(10i^-4j^-11k^) \overrightarrow{\mathrm{r}}=(11 \hat{i}-2 \hat{j}-8 \hat{\mathrm{k}})+\lambda(10 \hat{i}-4...
Find the image of the point (5, 9, 3) in the line
Find the image of the point $(5,9,3)$ in the line $\frac{\mathrm{x}-1}{2}=\frac{\mathrm{y}=2}{3}=\frac{\mathrm{z}-3}{4}$. Answer Given: Equation of line is...
Find the image of the point (0, 2, 3) in the line
Find the image of the point $(0,2,3)$ in the line $\frac{\mathrm{x}+3}{5}=\frac{\mathrm{y}-1}{2}=\frac{\mathrm{z}+4}{3}$. Answer Given: Equation of line is...
Find the coordinates of the foot of the perpendicular drawn from the point A(1, 8, 4) to the line joining the points B(0, -1, 3) and C(2, -3, -1).
Find the coordinates of the foot of the perpendicular drawn from the point $A(1,8,4)$ to the line joining the points $B(0,-1,3)$ and $C(2,-3,-1)$ Answer Given: perpendicular drawn from point...
Find the coordinates of the foot of the perpendicular drawn from the point A(1, 2, 1) to the line joining the points B(1, 4, 6) and C(5, 4, 4).
Find the coordinates of the foot of the perpendicular drawn from the point $A(1,2,1)$ to the line joining the points $B(1,4,6)$ and $C(5,4,4)$. Answer Given: perpendicular drawn from point...
Find the vector equation of a line passing through the point having the position vector
Find the vector equation of a line passing through the point having the position vector $(\hat{i}+2 \hat{j}-3 \hat{k})$ and parallel to the line joining the points with position vectors...
Find the vector equation of a line passing through the point A(3, -2, 1) and parallel to the line joining the points B(-2, 4, 2) and C(2, 3, 3). Also, find the Cartesian equations of the line.
Find the vector equation of a line passing through the point $A(3,-2,1)$ and parallel to the line joining the points $\mathrm{B}(-2,4,2)$ and $\mathrm{C}(2,3,3) .$ Also, find the Cartesian equations...
Find the vector and Cartesian equations of the line joining the points whose position vectors are
Find the vector and Cartesian equations of the line joining the points whose position vectors are $(\hat{i}-2 \hat{j}+\hat{k})$ and $(\hat{i}+3 \hat{j}-2 \hat{k})$ Answer Given: line passes through...
Find the vector and Cartesian equations of the line passing through the points A(2, -3, 0) and B(-2, 4, 3).
Find the vector and Cartesian equations of the line passing through the points $A(2,-3,0)$ and $B(-2,4,$, 3). Answer Given: line passes through the points $(2,-3,0)$ and $(-2,4,3)$ To find: equation...
Find the vector and Cartesian equations of the line passing through the points A(3, 4, -6) and B(5, -2, 7).
Find the equations of the line passing through the point $(1,-2,3)$ and parallel to the line $\frac{\mathrm{x}-6}{3}=\frac{\mathrm{y}-2}{-4}=\frac{\mathrm{Z}+7}{5}$. Also find the vector form of...
Find the coordinates of the foot of the perpendicular drawn from the point (1, 2, 3) to the line
Find the coordinates of the foot of the perpendicular drawn from the point $(1,2,3)$ to the line $\frac{\mathrm{x}-6}{3}=\frac{\mathrm{y}-7}{2}=\frac{\mathrm{z}-7}{-2}$. Also, find the length of the...
Show that the lines and do not intersect each other.
Show that the lines $\frac{\mathrm{x}-1}{2}=\frac{\mathrm{y}+1}{3}=z$ and $\frac{\mathrm{x}+1}{5}=\frac{\mathrm{y}-2}{1}, Z=2$ do not intersect each other. Answer Given: The equations of the two...
Show that the lines and intersect each other. Also, find the point of their intersection.
Show that the lines $\frac{\mathrm{x}-1}{2}=\frac{\mathrm{y}-2}{3}=\frac{\mathrm{Z}-3}{4}$ and $\frac{\mathrm{x}-4}{5}=\frac{\mathrm{y}-1}{2}=\mathrm{Z}$ intersect each other. Also, find the point...
Prove that the lines
Prove that the lines $\frac{\mathrm{x}-4}{1}=\frac{\mathrm{y}+3}{4}=\frac{\mathrm{z}+1}{7}$ and $\frac{\mathrm{x}-1}{2}=\frac{\mathrm{y}+1}{-3}=\frac{\mathrm{z}+10}{8}$ intersect each other and find...
Find the Cartesian and vector equations of the line passing through the point (1, 2, -4) and
Find the Cartesian and vector equations of the line passing through the point $(1,2,-4)$ and perpendicular to each of the lines...
Find the equations of the line passing through the point (-1, 3, -2) and perpendicular to each of the lines and
Find the equations of the line passing through the point $(-1,3,-2)$ and perpendicular to each of the lines $\frac{\mathrm{X}}{1}=\frac{\mathrm{y}}{2}=\frac{\mathrm{Z}}{3}$ and...
Find the Cartesian and vector equations of a line which passes through the point (1, 2, 3) and is parallel to the line
Find the Cartesian and vector equations of a line which passes through the point $(1,2,3)$ and is parallel to the line $\frac{-\mathrm{X}-2}{1}=\frac{\mathrm{y}+3}{7}=\frac{2 Z-6}{3}$ Answer Given:...
Find the equations of the line passing through the point (1, -2, 3) and parallel to the line Also find the vector form of this equation so obtained.
Find the equations of the line passing through the point $(1,-2,3)$ and parallel to the line $\frac{\mathrm{x}-6}{3}=\frac{\mathrm{y}-2}{-4}=\frac{\mathrm{Z}+7}{5}$. Also find the vector form of...
Find the Cartesian equations of the line which passes through the point (1, 3, -2) and is parallel to the line Also, find the vector form of the equations so obtained.
Find the Cartesian equations of the line which passes through the point $(1,3,-2)$ and is parallel to the line given by $\frac{\mathrm{x}+1}{3}=\frac{\mathrm{y}-4}{5}=\frac{\mathrm{z}+3}{-6}$. Also,...
The Cartesian equations of a line are 3x + 1 = 6y – 2 = 1 – z. Find the fixed point through which it passes, its direction ratios and also its vector equation.
The Cartesian equations of a line are $3 x+1=6 y-2=1-z$. Find the fixed point through which it passes, its direction ratios and also its vector equation. Answer Given: Cartesian equation of line are...
The Cartesian equations of a line Find the vector equation of the line.
The Cartesian equations of a line are $\frac{\mathrm{x}-3}{2}=\frac{\mathrm{y}+2}{-5}=\frac{\mathrm{Z}-6}{4}$. Find the vector equation of the line. Answer Given: Cartesian equation of line...
A line is drawn in the direction and it passes through a point with position vector Find the equations of the line in the vector as well as Cartesian forms.
A line is drawn in the direction of $(\hat{\mathrm{i}}+\hat{\mathrm{j}}-2 \hat{\mathrm{k}})$ and it passes through a point with position vector $(2 \hat{i}-\hat{j}-4 \hat{k}) .$ Find the equations...
Find the vector equation of the line passing through the point with position vector and parallel to the vector Deduce the Cartesian equations of the line.
Find the vector equation of the line passing through the point with position vector $(2 \hat{\mathrm{i}}+\hat{\mathrm{j}}-5 \hat{\mathrm{k}})$ and parallel to the vector $(\hat{i}+3...
A line passes through the point (2, 1, -3) and is parallel to the vector Find the equations of the line in vector and Cartesian forms.
A line passes through the point $(2,1,-3)$ and is parallel to the vector $(\hat{\mathrm{i}}-2 \hat{\mathrm{j}}+3 \hat{\mathrm{k}})$. Find the equations of the line in vector and Cartesian forms....
A line passes through the point (3, 4, 5) and is parallel to the vector Find the equations of the line in the vector as well as Cartesian forms.
Answer Given: line passes through point $(3,4,5)$ and is parallel to $2 \hat{\imath}+2 \hat{\jmath}-3 \hat{k}$ To find: equation of line in vector and Cartesian forms Formula Used: Equation of a...
Evaluate:
90C88 Answer : We know that: ⇒90C88=4005 Ans: ⇒90C88=4005
Evaluate:
16c13 Answer : We know that: nCr = ⇒16C13= ⇒16C13= ⇒16C13 = ⇒16C13 = ⇒16C13 = ⇒16C13 =560 Ans: 16C13=560
Evaluate:
21C4 Answer : We know that: nCr ⇒20C4 ⇒20C4 ⇒20C4 ⇒20C4 ⇒20C4 ⇒20C4 =4845 Ans: 20C4 =4845
Question consists of two statements, namely, Assertion (A) and Reason (R). For selecting the correct answer, use the following code:
(a) Both Assertion (A) and reason (R) are true and Reason (R) is a correct explanation of Assertion (A). (b) Both Assertion (A) and reason (R) are true and Reason (R) is not a correct explanation of...
Question consists of two statements, namely, Assertion (A) and Reason (R). For selecting the correct answer, use the following code:
(a) Both Assertion (A) and reason (R) are true and Reason (R) is a correct explanation of Assertion (A). (b) Both Assertion (A) and reason (R) are true and Reason (R) is not a correct explanation of...
Match the following:
The mean of 2, 7, 6 and x is 15 and mean of 18, 1, 6, x and y is 10. What is the value of y? (a) 5 (b) 10 (c) -20 (d) 30
If the median of the data 4, 7, x-1, x-3, 16, 25, written in ascending order, is 13 then x is equal to
(a) 13 (b) 14 (c) 15 (d) 16 Answer: (c) 15 Sol: Median of 6 numbers is the average of 3rd and 4th term. ∴ 13 = (????−1)+(????−3) 2 ⇒ 26 = 2x – 4 ⇒ 2x = 30 ⇒ x = 15 Thus, x is equal to...
The mean of 20 numbers is 0. OF them, at the most, how many may be greater than zero?
(a) 0 (b) 1 (c) 10 (d) 19 Answer: (d) 19 Sol: It is given that mean of 20 numbers is zero. i.e., average of 20 numbers is zero. i.e., sum of 20 numbers is zero. Thus, at most, there can be 19...
The median of the first 8 prime numbers is
(a) 7 (b) 9 (c) 11 (d) 13 Answer: (b) 9 Sol: First 8 prime numbers are 2, 3, 5, 7, 11, 13, 17 and 19. Median of 8 numbers is average of 4th and 5th terms.
Look at the cumulative frequency distribution table given below:
Answer: (c) 13 Sol: Converting the given data into a frequency table, we get: Hence, the number of families having an income range of Rs. 20,000 – Rs. 25,000 is 13. The correct option is...
For a symmetrical frequency distribution, we have:
(a) mean ˂ mode ˂ median (b) mean > mode > median (c) mean = mode = median (d) mode = 1 2 (mean + median) Answer: (c) mean = mode = median Sol: A symmetric distribution is one where the left...
The median and mode of a frequency distribution are 26 and 29 respectively. Then, the mean is
(a) 27.5 (b) 24.5 (c) 28.4 (d) 25.8 Answer: (b) 24.5 Sol: Mode = (3 × median) – (2 × mean) ⇒ (2 × mean) = (3 × median) – mode ⇒ (2 × mean) = 3 × 26 – 29 ⇒ (2 × mean) = 49 ⇒ Mean = 49 2 ∴ Mean = 24.5...
The mean and mode of a frequency distribution are 28 and 16 respectively. The median is
(a) 22 (b) 23.5 (c) 24 (d) 24.5 Answer: (c) 24 Sol: Mode = (3 × median) – (2 × mean) ⇒ (3 × median) = (mode + 2 mean) ⇒ (3 × median) = 16 + 56 ⇒ (3 × median) = 72 ⇒ Median = 72 3 ∴...
Consider the following table:
Look at the frequency distribution table given below:
If the mean and median of a set of numbers are 8.9 and 9 respectively, then the mode will be
(a) 7.2 (b) 8.2 (c) 9.2 (d) 10.2 Answer: (c) 9.2 Sol: It is given that the mean and median are 8.9 and 9, respectively, ∴ Mode = (3 × Median) – (2 × Mean) ⇒ Mode = (3 × 9) – (2 × 8.9) = 27 – 17.8 =...
Median =?
Mode = ?
Consider the following frequency distribution
Consider the frequency distribution of the heights of 60 students of a class
if the ‘less than type’ ogive and ‘more than type’ ogive intersect each other at (20.5, 15.5) then the median of the given data is
(a) 5.5 (b) 15.5 (c) 20.5 (d) 36.0 Answer: (c) 20.5 Sol: The x- coordinate represents the median of the given data. Thus, median of the given data is 20.5.
The relation between mean, mode and median is
(a) mode=(3 * mean) – (2 * median) (b) mode=(3 *median) – (2 *mean) (c) median=(3 * mean) – (2 * mode) (d) mean=(3 * median) – (2 *mode) Answer: (b) mode=(3 * median) – (2 *mean) Sol: mode=(3 *...
While computing the mean of the groue data, we assume that the frequencies are
(a) evenly distributed over the classes (b) centred at the class marks of the classes (c) centred at the lower limits of the classes (d) centred at the upper limits of the classes Answer: (b)...
In the formula for the following the mean of the grouped data, the i d ’s are the deviations from A of
(a) lower limits of the classes (b) upper limits of the classes (c) midpoints of the classes (d) none of these Answer: (c) midpoints of the classes Sol: The ???????? ′???? are the deviations from A...
For the finding the mean by using the formula,
If ‘ i x s are the midpoints of the class intervals of a grouped data, ‘ i f s are the corresponding frequencies and x is the mean then
The abscissa of the point of intersection of the Less Than Type and of the More Than Type cumulative frequency curves of a grouped data gives its
(a) Mean (b) Median (c) Mode (d)None of these Answer: (b) Median Sol: The abscissa of the point of intersection of the ‘less than type’ and that of the ‘more than type’ cumulative...
The cumulative frequency table is useful is determining the
(a) Mean (b) Median (c) Mode (d) all of these Answer: (b) Median Sol: The cumulative frequency table is useful in determining the median.
The medium of a frequency distribution is found graphically with the help of
(a) a histogram (b) a frequency curve (c) a frequency polygon (d) ogives Answer: (d) ogives Sol: This because median of a frequency distribution is found graphically...
The mode of frequency distribution is obtained graphically from
(a) a frequency curve (b) a frequency polygon (c) a histogram (d) an ogive Answer: (c) a histogram Sol: The mode of a frequency distribution can be obtained graphically from a histogram.
Which of the following measures of central tendency is influence by extreme values?
(a) Mean (b) Median (c) Mode (d) None of these Answer: (a) Mean Sol: Mean is influenced by extreme values.
Which of the following cannot be determined graphically?
(a) Mean (b) Median (c) Mode (d) None of these Answer: (a) Mean Sol: The mean cannot be determined graphically because the values cannot be summed.
Which of the following is not a measure of central tendency?
(a) Mean (b) Mode (c) Median (d) Standard Deviation Answer: (d) Standard Deviation Sol: The standard deviation is a measure of dispersion. It is the action or process of distributing...
Calculate the missing frequency form the following distribution, it being given that the median of the distribution is 24.
The following table, construct the frequency distribution of the percentage of marks obtained by 2300 students in a competitive examination.
The following table gives the life-time (in days) of 100 electric bulbs of a certain brand.
The following frequency distribution gives the monthly consumption of electricity ofr 64 consumers of locality.
In the following data, find the values of p and q. Also, find the median class and modal class.
The following are the ages of 300 patients getting medical treatment in a hospital on a particular day:
Find the mode of the given data:
What is the cumulative frequency of the modal class of the following distribution?
If the median of ???? 5 , ???? 4 , ???? 2 , ???? and ???? 3 , where x > 0, is 8, find the value of x. Hint Arranging the observations in ascending order, we have ????/ 5 , ???? /4 , ????/ 3 , ????/ 2 , ???? Median= ????/ 3 = 8.
If 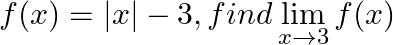
Answer:
Let 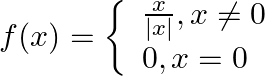 . Show that
. Show that 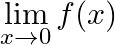 does not exist.
does not exist.
Answer:
Let 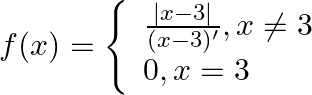 . Show that
. Show that 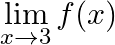 does not exist.
does not exist.
Answer:
Let 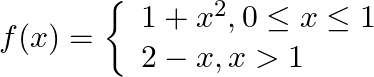 . Show that
. Show that 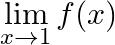 does not exist.
does not exist.
Answer:
Let 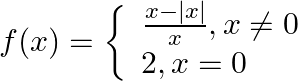 . Show that
. Show that 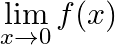 does not exist.
does not exist.
Answer:
Let 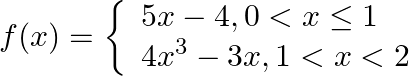 Find
Find 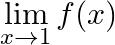
Answer:
Let 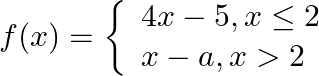 Find
Find 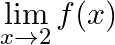
Answer:
Let 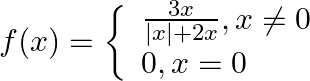 Show that
Show that 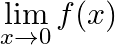 does not exist.
does not exist.
Answer:
Evaluate the following limits: 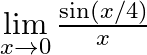
Answer:
Evaluate the following limits: 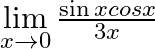
Answer:
Evaluate the following limits: 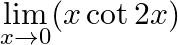
Answer:
Evaluate the following limits: 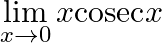
Answer:
Evaluate the following limits: 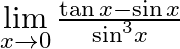
Answer:
Evaluate the following limits: 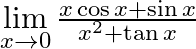
Answer:
Evaluate the following limits: 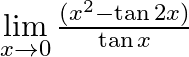
Answer:
Evaluate the following limits: 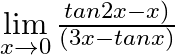
Answer:
Evaluate the following limits: 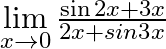
Answer:
Evaluate the following limits: 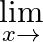 \pi
\pi  6
6
Answer:
Evaluate the following limits: 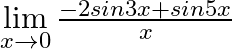
Answer:
Evaluate the following limits: 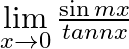
Answer:
Evaluate the following limits: 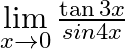
Answer:
Evaluate the following limits: 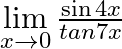
Answer:
Evaluate the following limits: 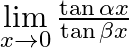
Answer:
Evaluate the following limits: 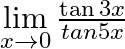
Answer:
Evaluate the following limits: 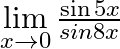
Answer:
Evaluate the following limits: 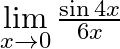
Answer:
Evaluate 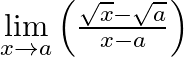
Answer:
Evaluate 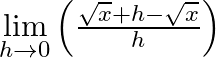
Answer:
Evaluate 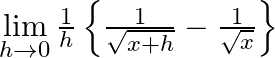
Answer:
Evaluate 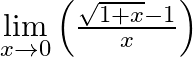
Answer:
Evaluate 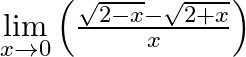
Answer:
Evaluate 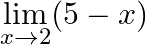
Answer:
Evaluate 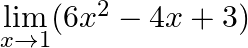
Answer:
Evaluate 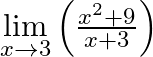
Answer:
Evaluate 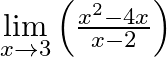
Answer:
Evaluate 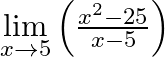
Answer:
Evaluate 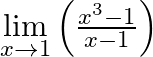
Answer:
Evaluate 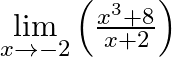
Answer:
Evaluate 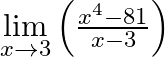
Answer:
Evaluate 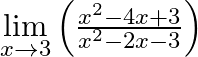
Answer:
Evaluate 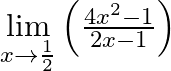
Answer:
Evaluate 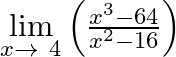
Answer:
Evaluate 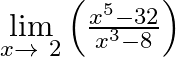
Answer:
Evaluate 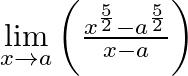
Answer:
Evaluate 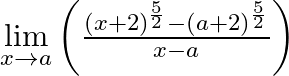
Answer:
Evaluate 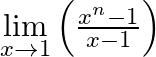
Answer:
For the binary operation ×10 set S = {1, 3, 7, 9}, find the inverse of 3.
Answer: 1 ×10 1 = remainder obtained by dividing 1 × 1 by 10 = 1 3 ×10 7 = remainder obtained by dividing 3 × 7 by 10 = 1 7 ×10 9 = remainder obtained by dividing 7 × 9 by 10 = 3 Composition table:...
Construct the composition table for ×5 on set Z5 = {0, 1, 2, 3, 4}
Answer: 1 ×5 1 = remainder obtained by dividing 1 × 1 by 5 = 1 3 ×5 4 = remainder obtained by dividing 3 × 4 by 5 = 2 4 ×5 4 = remainder obtained by dividing 4 × 4 by 5 = 1 Composition table: ×5 0 1...
Construct the composition table for ×6 on set S = {0, 1, 2, 3, 4, 5}.
Answer: 1 ×6 1 = remainder obtained by dividing 1 × 1 by 6 = 1 3 ×6 4 = remainder obtained by dividing 3 × 4 by 6 = 0 4 ×6 5 = remainder obtained by dividing 4 × 5 by 6 = 2 Composition table: ×6 0 1...
Construct the composition table for +5 on set S = {0, 1, 2, 3, 4}
Answer: 1 +5 1 = remainder obtained by dividing 1 + 1 by 5 = 2 3 +5 1 = remainder obtained by dividing 3 + 1 by 5 = 2 4 +5 1 = remainder obtained by dividing 4 + 1 by 5 = 3 Composition Table: +5 0 1...
Construct the composition table for ×4 on set S = {0, 1, 2, 3}.
Answer: Given, ×4 on set S = {0, 1, 2, 3} 1 ×4 1 = remainder obtained by dividing 1 × 1 by 4 = 1 0 ×4 1 = remainder obtained by dividing 0 × 1 by 4 = 0 2 ×4 3 = remainder obtained by dividing 2 × 3...
Let * be a binary operation on Z defined by a * b = a + b – 4 for all a, b ∈ Z. (i) Show that * is both commutative and associative. (ii) Find the identity element in Z
Answers: (i) Consider, a, b ∈ Z a * b = a + b – 4 = b + a – 4 = b * a a * b = b * a, ∀ a, b ∈ Z Then, * is commutative on Z. a * (b * c) = a * (b + c – 4) = a + b + c -4 – 4 = a + b + c – 8 (a * b)...
Let * be a binary operation on Q0 (set of non-zero rational numbers) defined by a * b = (3ab/5) for all a, b ∈ Q0. Show that * is commutative as well as associative. Also, find its identity element, if it exists.
Answer: Consider, a, b ∈ Q0 a * b = (3ab/5) = (3ba/5) = b * a a * b = b * a, for all a, b ∈ Q0 a * (b * c) = a * (3bc/5) = [a (3 bc/5)] /5 = 3 abc/25 (a * b) * c = (3 ab/5) * c = [(3 ab/5)...
Let * be a binary operation on Q – {-1} defined by a * b = a + b + ab for all a, b ∈ Q – {-1}. Then, (i) Show that * is both commutative and associative on Q – {-1} (ii) Find the identity element in Q – {-1}
Answers: (i) Consider, a, b ∈ Q – {-1} a * b = a + b + ab = b + a + ba = b * a a * b = b * a, ∀ a, b ∈ Q – {-1} a * (b * c) = a * (b + c + b c) = a + (b + c + b c) + a (b + c + b c) = a + b +...
Let * be a binary operation on Q – {-1} defined by a * b = a + b + ab for all a, b ∈ Q – {-1}. Then, Show that every element of Q – {-1} is invertible. Also, find inverse of an arbitrary element.
Answer: Consider, a ∈ Q – {-1} and b ∈ Q – {-1} be the inverse of a. a * b = e = b * a a * b = e and b * a = e a + b + ab = 0 and b + a + ba = 0 b (1 + a) = – a Q – {-1} b = -a/1 + a Q – {-1}...
Let A = R0 × R, where R0 denote the set of all non-zero real numbers. A binary operation ‘O’ is defined on A as follows: (a, b) O (c, d) = (ac, bc + d) for all (a, b), (c, d) ∈ R0 × R. (i) Show that ‘O’ is commutative and associative on A (ii) Find the identity element in A
Answers: (i) Consider, X = (a, b) Y = (c, d) ∈ A, ∀ a, c ∈ R0 b, d ∈ R X O Y = (ac, bc + d) Y O X = (ca, da + b) X O Y = Y O X, ∀ X, Y ∈ A O is not commutative on A. X = (a, b) Y = (c, d) a Z = (e,...
Let A = R0 × R, where R0 denote the set of all non-zero real numbers. A binary operation ‘O’ is defined on A as follows: (a, b) O (c, d) = (ac, bc + d) for all (a, b), (c, d) ∈ R0 × R. Find the invertible element in A.
Answer: Consider, F = (m, n) be the inverse in A ∀ m ∈ R0 and n ∈ R X O F = E F O X = E (am, bm + n) = (1, 0) and (ma, na + b) = (1, 0) Considering (am, bm + n) = (1, 0) am = 1 m = 1/a And bm + n =...
Let * be a binary operation on Z defined by a * b = a + b – 4 for all a, b ∈ Z. Find the invertible element in Z.
Answer: Consider, a ∈ Z and b ∈ Z be the inverse of a. a * b = e = b * a a * b = e and b * a = e a + b – 4 = 4 and b + a – 4 = 4 b = 8 – a ∈ Z Hence, 8 – a is the inverse of a ∈...
Find the identity element in the set of all rational numbers except – 1 with respect to * defined by a * b = a + b + ab
Answer: Consider, e be the identity element in I+ with respect to * such that a * e = a = e * a, ∀ a ∈ Q – {-1} a * e = a and e * a = a, ∀ a ∈ Q – {-1} a + e + ae = a and e + a + ea = a, ∀ a ∈ Q –...
Find the identity element in the set I+ of all positive integers defined by a * b = a + b for all a, b ∈ I+.
Answer: Consider, e be the identity element in I+ with respect to * a * e = a = e * a, ∀ a ∈ I+ a * e = a and e * a = a, ∀ a ∈ I+ a + e = a and e + a = a, ∀ a ∈ I+ e = 0, ∀ a ∈ I+ Hence, 0 is the...
The median of 19 observations is 30. Two more observation are made and the values of these are 8 and 32. Find the median of the 21 observations taken together. Hint Since 8 is less than 30 and 32 is more than 30, so the value of median (middle value) remains unchanged.
Sol: Since, 8 is less than 30 and 32 is more than 30, so the middle value remains unchanged Thus, the median of 21 observations taken together is 30.
The observation 29, 32, 48, 50, x, x+2, 72, 78, 84, 95 are arranged in ascending order. What is the value of x if the median of the data is 63?arranged in ascending order. What is the value of x if the median of the data is 63?
In a frequency distribution table with 12 classes, the class-width is 2.5 and the lowest class boundary is 8.1, then what is the upper class boundary of the highest class?
Sol: Upper class boundary = Lowest class boundary + width × number of classes = 8.1 + 2.5×12 = 8.1 + 30 = 38.1 Thus, upper class boundary of the highest class is 38.1.
