Answer
Given equations:

$\overline{\mathrm{r}}=(\hat{ı}+\hat{ȷ})+\lambda (2\hat{ı}–\hat{ȷ}+\hat{\mathrm{k}})$
\overline{\mathrm{r}}=(\hat{\imath}+\hat{\jmath})+\lambda(2 \hat{\imath}-\hat{\jmath}+\hat{\mathrm{k}})
$\overline{\mathrm{r}}=(2\hat{\mathrm{i}}+\hat{\mathrm{ȷ}}–\hat{\mathrm{k}})+\mu (3\hat{\mathrm{i}}–5\hat{\mathrm{ȷ}}+2\hat{\mathrm{k}})$
\overline{\mathrm{r}}=(2 \hat{\mathrm{i}}+\hat{\mathrm{\jmath}}-\hat{\mathrm{k}})+\mu(3 \hat{\mathrm{i}}-5 \hat{\mathrm{\jmath}}+2 \hat{\mathrm{k}})

To Find :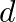
Formula :
1. Cross Product :
If 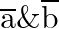are two vectors

$\begin{array}{l}\overline{\mathrm{a}}={\mathrm{a}}_1\hat{ı}+{\mathrm{a}}_2\hat{\mathrm{l}}+{\mathrm{a}}_3\hat{\mathrm{k}}\\ \overline{\mathrm{b}}={\mathrm{b}}_1\hat{\mathrm{l}}+{\mathrm{b}}_2\hat{\mathrm{ȷ}}+{\mathrm{b}}_3\hat{\mathrm{k}}\end{array}$
\begin{array}{l}
\overline{\mathrm{a}}=\mathrm{a}_{1} \hat{\imath}+\mathrm{a}_{2} \hat{\mathrm{l}}+\mathrm{a}_{3} \hat{\mathrm{k}} \\
\overline{\mathrm{b}}=\mathrm{b}_{1} \hat{\mathrm{l}}+\mathrm{b}_{2} \hat{\mathrm{\jmath}}+\mathrm{b}_{3} \hat{\mathrm{k}}
\end{array}

then,

$\overline{\mathrm{a}}\times \overline{\mathrm{b}}=\left|\begin{array}{ccc}\hat{\mathrm{l}}& \hat{\mathrm{l}}& \hat{\mathrm{k}}\\ {\mathrm{a}}_1& {\mathrm{a}}_2& {\mathrm{a}}_3\\ {\mathrm{ }\mathrm{b}}_1& {\mathrm{ }\mathrm{b}}_2& {\mathrm{ }\mathrm{b}}_3\end{array}\right|$
\overline{\mathrm{a}} \times \overline{\mathrm{b}}=\left|\begin{array}{ccc}
\hat{\mathrm{l}} & \hat{\mathrm{l}} & \hat{\mathrm{k}} \\
\mathrm{a}_{1} & \mathrm{a}_{2} & \mathrm{a}_{3} \\
\mathrm{~b}_{1} & \mathrm{~b}_{2} & \mathrm{~b}_{3}
\end{array}\right|

2. Dot Product :
If 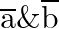are two vectors

$\begin{array}{l}\overline{\mathrm{a}}={\mathrm{a}}_1\hat{ı}+{\mathrm{a}}_2\hat{ȷ}+{\mathrm{a}}_3\hat{\mathrm{k}}\\ \overline{\mathrm{b}}={\mathrm{b}}_1\hat{ı}+{\mathrm{b}}_2\hat{ȷ}+{\mathrm{b}}_3\hat{\mathrm{k}}\end{array}$
\begin{array}{l}
\overline{\mathrm{a}}=\mathrm{a}_{1} \hat{\imath}+\mathrm{a}_{2} \hat{\jmath}+\mathrm{a}_{3} \hat{\mathrm{k}} \\
\overline{\mathrm{b}}=\mathrm{b}_{1} \hat{\imath}+\mathrm{b}_{2} \hat{\jmath}+\mathrm{b}_{3} \hat{\mathrm{k}}
\end{array}

then,

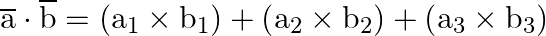
3. Shortest distance between two lines :
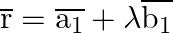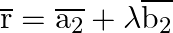The shortest distance between the skew lines and is given by,

$\mathrm{d}=\left|\frac{\left(\overline{{\mathrm{b}}_1}\times \overline{{\mathrm{b}}_2}\right)·\left(\overline{{\mathrm{a}}_2}–\overline{{\mathrm{a}}_1}\right)}{\left|\overline{{\mathrm{b}}_1}\times \overline{{\mathrm{b}}_2}\right|}\right|$
\mathrm{d}=\left|\frac{\left(\overline{\mathrm{b}_{1}} \times \overline{\mathrm{b}_{2}}\right) \cdot\left(\overline{\mathrm{a}_{2}}-\overline{\mathrm{a}_{1}}\right)}{\left|\overline{\mathrm{b}_{1}} \times \overline{\mathrm{b}_{2}}\right|}\right|

Answer:
For given lines,

$\begin{array}{l}\overline{\mathrm{r}}=(\hat{\mathrm{i}}+\hat{\mathrm{j}})+\lambda (2\hat{\mathrm{i}}–\hat{\mathrm{j}}+\hat{\mathrm{k}})\\ \overline{\mathrm{r}}=(2\hat{\mathrm{i}}+\hat{\mathrm{j}}–\hat{\mathrm{k}})+\mu (3\hat{ı}–5\hat{\mathrm{j}}+2\hat{\mathrm{k}})\end{array}$
\begin{array}{l}
\overline{\mathrm{r}}=(\hat{\mathrm{i}}+\hat{\mathrm{j}})+\lambda(2 \hat{\mathrm{i}}-\hat{\mathrm{j}}+\hat{\mathrm{k}}) \\
\overline{\mathrm{r}}=(2 \hat{\mathrm{i}}+\hat{\mathrm{j}}-\hat{\mathrm{k}})+\mu(3 \hat{\imath}-5 \hat{\mathrm{j}}+2 \hat{\mathrm{k}})
\end{array}

Here,

$\begin{array}{l}\overline{{\mathrm{a}}_1}=\hat{\mathrm{l}}+\hat{\mathrm{ȷ}}\\ \overline{{\mathrm{b}}_1}=2\hat{\mathrm{l}}–\hat{\mathrm{ȷ}}+\hat{\mathrm{k}}\end{array}$
\begin{array}{l}
\overline{\mathrm{a}_{1}}=\hat{\mathrm{l}}+\hat{\mathrm{\jmath}} \\
\overline{\mathrm{b}_{1}}=2 \hat{\mathrm{l}}-\hat{\mathrm{\jmath}}+\hat{\mathrm{k}}
\end{array}
$\begin{array}{l}\overline{{\mathrm{a}}_2}=2\hat{\mathrm{l}}+\hat{\mathrm{ȷ}}–\hat{\mathrm{k}}\\ \overline{{\mathrm{b}}_2}=3\hat{\mathrm{i}}–5\hat{\mathrm{j}}+2\hat{\mathrm{k}}\end{array}$
\begin{array}{l}
\overline{\mathrm{a}_{2}}=2 \hat{\mathrm{l}}+\hat{\mathrm{\jmath}}-\hat{\mathrm{k}} \\
\overline{\mathrm{b}_{2}}=3 \hat{\mathrm{i}}-5 \hat{\mathrm{j}}+2 \hat{\mathrm{k}}
\end{array}

Therefore,

$\begin{array}{l}\overline{{\mathrm{b}}_1}\times \overline{{\mathrm{b}}_2}=\left|\begin{array}{ccc}\hat{ı}& \hat{ȷ}& \hat{\mathrm{k}}\\ 2& –1& 1\\ 3& –5& 2\end{array}\right|\\ =\hat{\mathrm{i}}(–2+5)–\hat{\mathrm{ȷ}}(4–3)+\hat{\mathrm{k}}(–10+3)\\ \therefore \overline{{\mathrm{b}}_1}\times \overline{{\mathrm{b}}_2}=3\hat{\mathrm{i}}–\hat{\mathrm{ȷ}}–7\hat{\mathrm{k}}\\ \therefore \left|\overline{{\mathrm{b}}_1}\times \overline{{\mathrm{b}}_2}\right|=\sqrt{3^2+(–1{)}^2+(–7{)}^2}\\ =\sqrt{9+1+49}\\ =\sqrt{59}\\ \overline{{\mathrm{a}}_2}–\overline{{\mathrm{a}}_1}=(2–1)\hat{\mathrm{i}}+(1–1)\hat{\mathrm{j}}+(–1–0)\hat{\mathrm{k}}\\ \therefore \overline{{\mathrm{a}}_2}–\overline{{\mathrm{a}}_1}=\hat{\mathrm{l}}+0\hat{\mathrm{ȷ}}–\hat{\mathrm{k}}\end{array}$
\begin{array}{l}
\overline{\mathrm{b}_{1}} \times \overline{\mathrm{b}_{2}}=\left|\begin{array}{ccc}
\hat{\imath} & \hat{\jmath} & \hat{\mathrm{k}} \\
2 & -1 & 1 \\
3 & -5 & 2
\end{array}\right| \\
=\hat{\mathrm{i}}(-2+5)-\hat{\mathrm{\jmath}}(4-3)+\hat{\mathrm{k}}(-10+3) \\
\therefore \overline{\mathrm{b}_{1}} \times \overline{\mathrm{b}_{2}}=3 \hat{\mathrm{i}}-\hat{\mathrm{\jmath}}-7 \hat{\mathrm{k}} \\
\therefore\left|\overline{\mathrm{b}_{1}} \times \overline{\mathrm{b}_{2}}\right|=\sqrt{3^{2}+(-1)^{2}+(-7)^{2}} \\
=\sqrt{9+1+49} \\
=\sqrt{59} \\
\overline{\mathrm{a}_{2}}-\overline{\mathrm{a}_{1}}=(2-1) \hat{\mathrm{i}}+(1-1) \hat{\mathrm{j}}+(-1-0) \hat{\mathrm{k}} \\
\therefore \overline{\mathrm{a}_{2}}-\overline{\mathrm{a}_{1}}=\hat{\mathrm{l}}+0 \hat{\mathrm{\jmath}}-\hat{\mathrm{k}}
\end{array}

Now,

$\begin{array}{l}\left(\overline{b_1}\times \overline{b_2}\right)·\left(\overline{a_2}–\overline{a_1}\right)=(3\hat{ı}–\hat{ȷ}–7\hat{k})·(\hat{ı}+0\hat{ȷ}–\hat{k})\\ =(3\times 1)+\left(\right(–1)\times 0)+\left(\right(–7)\times (–1\left)\right)\\ =3+0+7\end{array}$
\begin{array}{l}
\left(\overline{b_{1}} \times \overline{b_{2}}\right) \cdot\left(\overline{a_{2}}-\overline{a_{1}}\right)=(3 \hat{\imath}-\hat{\jmath}-7 \hat{k}) \cdot(\hat{\imath}+0 \hat{\jmath}-\hat{k}) \\
=(3 \times 1)+((-1) \times 0)+((-7) \times(-1)) \\
=3+0+7
\end{array}
$=10$
=10

Therefore, the shortest distance between the given lines is

$\begin{array}{l}\mathrm{d}=\left|\frac{\left(\overline{{\mathrm{b}}_1}\times \overline{{\mathrm{b}}_2}\right)·\left(\overline{{\mathrm{a}}_2}–\overline{{\mathrm{a}}_1}\right)}{\left|\overline{{\mathrm{b}}_1}\times \overline{{\mathrm{b}}_2}\right|}\right|\\ \therefore \mathrm{d}=\left|\frac{10}{\sqrt{59}}\right|\end{array}$
\begin{array}{l}
\mathrm{d}=\left|\frac{\left(\overline{\mathrm{b}_{1}} \times \overline{\mathrm{b}_{2}}\right) \cdot\left(\overline{\mathrm{a}_{2}}-\overline{\mathrm{a}_{1}}\right)}{\left|\overline{\mathrm{b}_{1}} \times \overline{\mathrm{b}_{2}}\right|}\right| \\
\therefore \mathrm{d}=\left|\frac{10}{\sqrt{59}}\right|
\end{array}