A line passes through the point $(2,1,-3)$ and is parallel to the vector $(\hat{\mathrm{i}}-2 \hat{\mathrm{j}}+3 \hat{\mathrm{k}})$. Find the equations of the line in vector and Cartesian forms....
Find the maximum and minimum values of 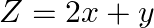 , subject to the constraints
, subject to the constraints 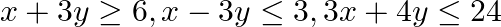
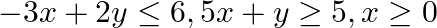 and
and 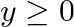
The feasible region determined by $x+3 y \geq 6, x-3 y \leq 3,3 x+4 y \leq 24$ $-3 x+2 y \leq 6,5 x+y \geq 5, x \geq 0$ and $y \geq 0$ is given by The corner points of the feasible region are $A(4 /...
Draw a cumulative frequency curve for the following data :
Marks obtained 0-10 10-20 20-30 30-40 40-50 No. of students 8 10 22 40 20 Hence determine: (i) the median (ii) the pass marks if 85% of the students pass. (iii) the marks which 45% of the...
Using the data given below, construct the cumulative frequency table and draw the ogive. From the ogive, estimate : (i) the median (ii) the inter quartile range.
Marks 0-10 10-20 20-30 30-40 40-50 50-60 60-70 70-80 Frequency 3 8 12 14 10 6 5 2 Also state the median class Solution: Arranging the data in cumulative frequency table. Marks Frequency Cumulative...
Calculate the mean, the median and the mode of the following distribution.
Age in years 12 13 14 15 16 17 18 No. of students 2 3 5 6 4 3 2 Solution: Age in years xi No. of students fi Cumulative frequency fixi 12 2 2 24 13 3 5 39 14 5 10 70 15 6 16 90 16 4 20 64 17 3 23 51...
Find the median and mode for the set of numbers : 2, 2, 3, 5, 5, 5, 6, 8, 9
Solution: Here n = 9 which is odd. Median = ((n+1)/2)th term Median = ((9+1)/2)th term Median = (10/2)th term Median = 5 th term Median = 5 Mode is the number which appears most often in a set of...
The marks scored by 16 students in a class test are : 3, 6, 8, 13, 15, 5, 21, 23, 17, 10, 9, 1, 20, 21, 18, 12 Find (i) the median (ii) lower quartile (iii) upper quartile
Solution: Arranging data in ascending order 1,3,5,6,8,9,10,12,13,15,17,18,20,21,21,23 Here n = 16 which is even (i) So median = ½ ( n/2 th term + ((n/2)+1)th term) = ½ (16/2 th term +...
Find the median of: 17, 26, 60, 45, 33, 32, 29, 34, 56 . If 26 is replaced by 62, find the new median.
Solution: Arranging numbers in ascending order 17,26,29,32,33,34,45,56,60 Here n = 9 which is odd. So Median =( (n+1)/2) th term Median = ((9+1)/2)th term Median = (10/2)th term Median = 5th term...
If the median of 5, 9, 11, 3, 4, x, 8 is 6, find the value of x.
Solution: Arranging numbers in ascending order 3,4,5,x,8,9,11 Here n = 7 which is odd Given median = 6 So Median =( (n+1)/2) th term 6 = ((7+1)/2)th term 6 = ((8/2)th term 6 = 4th term 6 = x Hence...
Graph the solution sets of the following inequations: 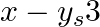
Given $x-y \leq 3$ $\Rightarrow-y \leq 3-x$ Multiplying by minus on both the sides, we'll get $\begin{array}{l} y \geq-3+x \\ y \geq x-3 \end{array}$ Consider the equation $y=x-3$. Finding points on...
The measures of the diameter of the heads of 150 screw is given in the following table. If the mean diameter of the heads of the screws is 51.2 mm, find the values of p and q .
Diameter in mm 32-36 37-41 42-46 47-51 52-56 57-61 62-66 No. of screws 15 17 p 25 q 20 30 Solution: Given mean = 51.2 mm The given distribution is not continuous. Adjustment factor = (37-36)/2 = ½ =...
The daily expenditure of 100 families are given below. Calculate f1, and f2, if the mean daily expenditure is Rs 188.
Expenditure in Rs 140-160 160-180 180-200 200-220 220-240 No. of families 5 25 f1 f2 5 Solution: Given mean = 188 Class Frequency fi Class mark xi fixi 140-160 5 150 750 160-180 25 170 4250 180-200...
The mean of the following frequency distribution is 62.8. Find the value of p.
Class 0-20 20-40 40-60 60-80 80-100 100-120 Frequency 5 8 p 12 7 8 Solution: Class Frequency fi Class mark xi fixi 0-20 5 10 50 20-40 8 30 240 40-60 p 50 50p 60-80 12 70 840 80-100 7 90 630 100-120...
Calculate the Arithmetic mean, correct to one decimal place, for the following frequency
Marks 10-20 20-30 30-40 40-50 50-60 60-70 70-80 80-90 90-100 Students 2 4 5 16 20 10 6 8 4 Solution: Class mark, xi = (upper class limit + lower class limit)/2 Marks Students fi Class mark xi fixi...
Find the value of p if the mean of the following distribution is 18.
Variate (xi) 13 15 17 19 20+p 23 Frequency (fi) 8 2 3 4 5p 6 Solution: Variate (xi) Frequency (fi) fi xi 13 8 104 15 2 30 17 3 51 19 4 76 20+p 5p 5p2+100p 23 6 138 Total Ʃfi = 23+5p Ʃfi xi =...
Find the value of p for the following distribution whose mean is 20.6.
Variate (xi) 10 15 20 25 35 Frequency (fi) 3 10 p 7 5 Solution: Variate (xi) Frequency (fi) fx 10 3 30 15 10 150 20 p 20p 25 7 175 35 5 175 Total Ʃfi = 25+p Ʃfi xi = 530+20p Mean = Ʃfx/Ʃf 20.6 =...
The heights of 50 children were measured (correct to the nearest cm) giving the following results
Height (in cm) 65 66 67 68 69 70 71 72 73 No. of children 1 4 5 7 11 10 6 4 2 Calculate the mean height for this distribution correct to one place of decimal. Solution: Height x No. of children f...
The contents of 50 boxes of matches were counted giving the following results.
No. of matches 41 42 43 44 45 46 No. of boxes 5 8 13 12 7 5 Calculate the mean number of matches per box. Solution: No. o f matches x No. of boxes f fx 41 5 205 42 8 336 43 13 559 44 12 528 45 7 315...
There are 50 students in a class of which 40 are boys and the rest girls. The average weight of the students in the class is 44 kg and average weight of the girls is 40 kg. Find the average weight of boys.
Solution: Total number of students = 50 No. of boys = 40 No. of girls = 50-40 = 10 Average weight of 50 students = 44 kg So sum of weight = 44×50 = 2200 kg Average weight of girls = 40 kg So sum of...
The average height of 30 students is 150 cm. It was detected later that one value of 165 cm was wrongly copied as 135 cm for computation of mean. Find the correct mean.
Solution: Average height of 30 students = 150 cm So sum of height = 150×30 = 4500 Difference between correct value and wrong value = 165-135 = 30 So actual sum = 4500+30 = 4530 So actual mean =...
The mean of 20 numbers is 18. If 3 is added to each of the first ten numbers, find the mean of new set of 20 numbers.
Solution: Given the mean of 20 numbers = 18 Sum of numbers = 18×20 = 360 If 3 is added to each of first 10 numbers, then new sum = (3×10)+360 = 30+360 = 390 New mean = 390/20 = 19.5 Hence the mean...
Arun scored 36 marks in English, 44 marks in Civics, 75 marks in Mathematics and x marks in Science. If he has scored an average of 50 marks, find x.
Solution: Marks scored in English = 36 Marks scored in Civics = 44 Marks scored in Mathematics = 75 Marks scored in Science = x No. of subjects = 4 Average marks = sum of marks / No. of subjects =...
100 pupils in a school have heights as tabulated below
Height in cm 121-130 131-140 141-150 151-160 161-170 171-180 No. of pupils 12 16 30 20 14 8 Draw the ogive for the above data and from it determine the median (use graph paper). Solution: We write...
The following distribution represents the height of 160 students of a school.
Height 140-145 145-150 150-155 155-160 160-165 165-170 170-175 175-180 No. of students 12 20 30 38 24 16 12 8 Draw an ogive for the given distribution taking 2 cm = 5 cm of height on one axis and 2...
The marks obtained by 120 students in a Mathematics test are-given below
Marks 0-10 10-20 20-30 30-40 40-50 50-60 60-70 70-80 80-90 90-100 No. of students 5 9 16 22 26 18 11 6 4 3 Draw an ogive for the given distribution on a graph sheet. Use a suitable scale for ogive...
Using a graph paper, draw an ogive for the following distribution which shows a record of the weight in kilograms of 200 students
Weight 40-45 45-50 50-55 55-60 60-65 65-70 70-75 75-80 Frequency 5 17 22 45 51 31 20 9 Use your ogive to estimate the following: (i) The percentage of students weighing 55 kg or more. (ii) The...
The monthly income of a group of 320 employees in a company is given below
Monthly income No. of employees 6000-7000 20 7000-8000 45 8000-9000 65 9000-10000 95 10000-11000 60 11000-12000 30 12000-13000 5 Draw an ogive of the given distribution on a graph sheet taking 2 cm...
Marks obtained by 200 students in an examination are given below
marks 0-10 10-20 20-30 30-40 40-50 50-60 60-70 70-80 80-90 90-100 No. of students 5 11 10 20 28 37 40 29 14 6 Draw an ogive for the given distribution taking 2 cm = 10 marks on one axis and 2 cm =...
The daily wages of 80 workers in a project are given below
Wages in Rs 400-450 450-500 500-550 550-600 600-650 650-700 700-750 No. of workers 2 6 12 18 24 13 5 Use a graph paper to draw an ogive for the above distribution. ( a scale of 2 cm = Rs 50 on x-...
The table shows the distribution of scores obtained by 160 shooters in a shooting competition. Use a graph sheet and draw an ogive for the distribution. (Take 2 cm = 10 scores on the x-axis and 2 cm = 20 shooters on the y-axis)
Scores 0-10 10-20 20-30 30-40 40-50 50-60 60-70 70-80 80-90 90-100 No. of shooters 9 13 20 26 30 22 15 10 8 7 Use your graph to estimate the following: (i) The median. (ii) The interquartile...
The weight of 50 workers is given below:
Weight in kg 50-60 60-70 70-80 80-90 90-100 100-110 110-120 No. of workers 4 7 11 14 6 5 3 Draw an ogive of the given distribution using a graph sheet. Take 2 cm = 10 kg on one axis , and 2 cm = 5...
Attempt this question on graph paper.
Age( yrs) 5-15 15-25 25-35 35-45 45-55 55-65 65-75 No. of casualities due to accidents 6 10 15 13 24 8 7 (i) Construct the ‘less than’ cumulative frequency curve for the above data, using 2 cm = 10...
Use graph paper for this question. The following table shows the weights in gm of a sample of 100 potatoes taken from a large consignment:
Weight (gm) 50-60 60-70 70-80 80-90 90-100 100-110 110-120 120-130 Frequency 8 10 12 16 18 14 12 10 (i) Calculate the cumulative frequencies. (ii) Draw the cumulative frequency curve and from it...
Using the data given below construct the cumulative frequency table and draw the-Ogive. From the ogive determine the median.
Marks 0-10 10-20 20-30 30-40 40-50 50-60 60-70 70-80 No. of students 3 8 12 14 10 6 5 2 Solution: We write the given data in cumulative frequency table. Marks No of students f Cumulative frequency...
The following table shows the distribution of the heights of a group of a factory workers.
Height ( in cm ) 150-155 155-160 160-165 165-170 170-175 175-180 180-185 No. of workers 6 12 18 20 13 8 6 (i) Determine the cumulative frequencies. (ii) Draw the cumulative frequency curve on a...
33:
Marks obtained 24-29 29-34 34-39 39-44 44-49 49-54 54-59 No. of students 1 2 5 6 4 3 2 Solution: We write the given data in cumulative frequency table. Marks obtained No of students Cumulative...
Draw an ogive for the following data:
Class intervals 1-10 11-20 21-30 31-40 41-50 51-60 Frequency 3 5 8 7 6 2 Solution: The given distribution is not continuous. Adjustment factor = (11-10)/2 = ½ = 0.5 We subtract 0.5 from lower limit...
Draw an ogive for the following frequency distribution:
Height ( in cm ) 150-160 160-170 170-180 180-190 190-200 No. of students 8 3 4 10 2 Solution: We write the given data in cumulative frequency table. Height in cm No of students Cumulative frequency...
Find the mode of the following distribution by drawing a histogram
Mid value 12 18 24 30 36 42 48 Frequency 20 12 8 24 16 8 12 Also state the modal class. Solution: Mid value Frequency 12 20 18 12 24 8 30 24 36 16 42 8 48 12 Here mid value and frequency is given....
Use a graph paper for this question. The daily pocket expenses of 200 students in a school are given below:
Pocket expenses (in Rs) Number of students (Frequency ) 0-5 10 5-10 14 10-15 28 15-20 42 20-25 50 25-30 30 30-35 14 35-40 12 Draw a histogram representing the above distribution and estimate the...
IQ of 50 students was recorded as follows.
IQ score 80-90 90-100 100-110 110-120 120-130 130-140 No. of students 6 9 16 13 4 2 Draw a histogram for the above data and estimate the mode. Solution: Construct histogram using given data....
Draw a histogram and estimate the mode for the following frequency distribution :
Classes 0-10 10-20 20-30 30-40 40-50 50-60 Frequency 2 8 10 5 4 3 Solution: Construct histogram using given data. Classes 0-10 10-20 20-30 30-40 40-50 50-60 Frequency 2 8 10 5 4 3 Represent classes...
A Mathematics aptitude test of 50 students was recorded as follows :
Marks 50-60 60-70 70-80 80-90 90-100 No. of students 4 8 14 19 5 Draw a histogram for the above data using a graph paper and locate the mode. (2011) Solution: Construct histogram using given data....
Find the modal height of the following distribution by drawing a histogram :
Height (in cm) 140-150 150-160 160-170 170-180 180-190 No. of students 7 6 4 10 2 Solution: Construct histogram using given data. Height (in cm) 140-150 150-160 160-170 170-180 180-190 No. of...
Draw a histogram for the following frequency distribution and find the mode from the graph :
Class 0-5 5-10 10-15 15-20 20-25 25-30 Frequency 2 5 18 14 8 5 Solution: Construct histogram using given data. Class 0-5 5-10 10-15 15-20 20-25 25-30 Frequency 2 5 18 14 8 5 Represent class on...
The following table gives the weekly wages (in Rs.) of workers in a factory :
Weekly wages (in Rs) 50-55 55-60 60-65 65-70 70-75 75-80 80-85 85-90 No. of workers 5 20 10 10 9 6 12 8 Calculate: (i) The mean. (ii) the modal class (iii) the number of workers getting weekly wages...
(i) Using step-deviation method, calculate the mean marks of the following distribution.
(ii) State the modal class.
Class interval 50-55 55-60 60-65 65-70 70-75 75-80 80-85 85-90 Frequency 5 20 10 10 9 6 12 8 Solution: (i) Class mark (xi) = (upper limit + lower limit)/2 Let assumed mean (A) = 67.5 Class size (h)...
The distribution given below shows the marks obtained by 25 students in an aptitude test. Find the mean, median and mode of the distribution.
Marks obtained 5 6 7 8 9 10 No. of students 3 9 6 4 2 1 Solution: We write the marks in cumulative frequency table. Marks x Frequency (f) fx Cumulative frequency 5 3 15 3 6 9 54 12 7 6 42 18 8 4 32...
The marks obtained by 30 students in a class assessment of 5 marks is given below:
Marks 0 1 2 3 4 5 No. of students 1 3 6 10 5 5 Calculate the mean, median and mode of the above distribution. Solution: We write the data in cumulative frequency table. Marks x Frequency (f)...
Find the mode and median of the following frequency distribution :
x 10 11 12 13 14 15 f 1 4 7 5 9 3 Solution: We write the data in cumulative frequency table. x Frequency (f) Cumulative frequency 10 1 1 11 4 5 12 7 12 13 5 17 14 9 26 15 3 29 Here number of...
A boy scored the following marks in various class tests during a term each test being marked out of 20: 15, 17, 16, 7, 10, 12, 14, 16, 19, 12, 16
(i) What are his modal marks ?
(ii) What are his median marks ?
(iii) What are his mean marks ?
Solution: (i)We arrange given marks in ascending order 7, 10, 12, 12, 14, 15, 16, 16, 16, 17, 19 16 appears maximum number of times. Hence his modal mark is 16. (ii)Here number of observations, n =...
The marks of 10 students of a class in an examination arranged in ascending order are as follows: 13, 35, 43, 46, x, x +4, 55, 61,71, 80 If the median marks is 48, find the value of x. Hence, find the mode of the given data. (2017)
Solution: Given data in ascending order: 13, 35, 43, 46, x, x +4, 55, 61,71, 80 Given median = 48 Number of observations, n = 10 which is even. median = ½ ( n/2 th term + ((n/2)+1)th term) 48 = ½...
Calculate the mean, the median and the mode of the following numbers : 3, 1, 5, 6, 3, 4, 5, 3, 7, 2
Solution: We arrange given data in ascending order 1, 2, 3, 3, 3, 4, 5, 5, 6, 7 Mean = Ʃxi/n = (1+2+3+3+3+4+5+5+6+7)/10 = 39/10 = 3.9 Here number of observations, n = 10 which is even. So median = ½...
Find the mean, median and mode of the following distribution : 8, 10, 7, 6, 10, 11, 6, 13, 10
Solution: We arrange given data in ascending order 6, 6, 7, 8, 10, 10, 10, 11, 13 Mean = Ʃxi/n = (6+6+7+8+10+10+10+11+13)/9 = 81/9 = 9 Hence the mean is 9. Here number of observations, n = 9 which...
Calculate the mean, the median and the mode of the numbers : 3, 2, 6, 3, 3, 1, 1, 2
Solution: We arrange given data in ascending order 1, 1, 2, 2, 3, 3, 3, 6 Mean = Ʃxi/n = (1+1+2+2+3+3+3+6)/8 = 21/8 = 2.625 Hence the mean is 2.625. Here number of observations, n = 8 which is even....
Find the mode of the following sets of numbers ;
(i) 3, 2, 0, 1, 2, 3, 5, 3
(ii) 5, 7, 6, 8, 9, 0, 6, 8, 1, 8
(iii) 9, 0, 2, 8, 5, 3, 5, 4, 1, 5, 2, 7
Solution: Mode is the number which appears most often in a set of numbers. (i)Given set is 3, 2, 0, 1, 2, 3, 5, 3. In this set, 3 occurs maximum number of times. Hence the mode is 3. (ii) Given set...
For the following frequency distribution, find :
(i) the median
(ii) lower quartile
(iii) upper quartile
Variate 25 31 34 40 45 48 50 60 Frequency 3 8 10 15 10 9 6 2 Solution: We write the variates in cumulative frequency table. Variate Frequency (f) Cumulative frequency 25 3 3 31 8 11 34 10 21 40 15...
From the following frequency distribution, find :
(i) the median
(ii) lower quartile
(iii) upper quartile
(iv) inter quartile range
Variate 15 18 20 22 25 27 30 Frequency 4 6 8 9 7 8 6 Solution: We write the variates in cumulative frequency table. Variate Frequency (f) Cumulative frequency 15 4 4 18 6 10 20 8 18 22 9 27 25 7 34...
The daily wages in (rupees of) 19 workers are 41, 21, 38, 27, 31, 45, 23, 26, 29, 30, 28, 25, 35, 42, 47, 53, 29, 31, 35. find :
(i) the median
(ii) lower quartile
(iii) upper quartile
(iv) inter quartile range
Solution: Arranging the observations in ascending order 21, 23, 25, 26, 27, 28, 29, 29, 30, 31, 31, 35, 35, 38, 41, 42, 45, 47, 53 Here n = 19 which is odd. (i)Median = ((n+1)/2)th term = (19+1)/2 =...
Calculate the mean and the median for the following distribution :
Number 5 10 15 20 25 30 35 Frequency 1 2 5 6 3 2 1 Solution: We write the numbers in cumulative frequency table. Marks (x) No. of students (f) Cumulative frequency fx 5 1 1 5 10 2 3 20 15 5 8 75 20...
Marks obtained by 70 students are given below :
Marks 20 70 50 60 75 90 40 No. of students 8 12 18 6 9 5 12 Calculate the median marks. Solution: We write the marks in ascending order in cumulative frequency table. Marks No. of students (f)...
Find the median for the following distribution.
Marks 35 45 50 64 70 72 No. of students 3 5 8 10 5 5 Solution: We write the distribution in cumulative frequency table. Marks No. of students (f) Cumulative frequency 35 3 3 45 5 8 50 8 16 64 10 26...
Find the median for the following distribution:
Wages per day in Rs. 38 45 48 55 62 65 No. of workers 14 8 7 10 6 2 Solution: We write the distribution in cumulative frequency table. Wages per day in Rs. No. of workers (f) Cumulative frequency 38...
The mean of the numbers 1, 7, 5, 3, 4, 4, is m. The numbers 3, 2, 4, 2, 3, 3, p have mean m-1 and median q. Find
(i) p
(ii) q
(iii) the mean of p and q.
Solution: (i) Mean of 1, 7, 5, 3, 4, 4 is m. Here n = 6 Mean, m = (1+7+5+3+4+4)/6 m = 24/6 m = 4 Given the numbers 3, 2, 4, 2, 3, 3, p have mean m-1. So m-1 = (3+2+4+2+3+3+p)/7 4-1 = (17+p)/7 3 =...
The median of the observations 11, 12, 14, (x – 2), (x + 4), (x + 9), 32, 38, 47 arranged in ascending order is 24. Find the value of x and hence find the mean.
Solution: Observation are as follows : 11, 12, 14, (x-2), (x+4), (x+9), 32, 38, 47 n = 9 Here n is odd. So median = ((n+1)/2)th term = (9+1)/2 )th term = 5th term = x+4 Given median = 24 x+4 = 24 x...
Calculate the mean and the median of the numbers : 2, 1, 0, 3, 1, 2, 3, 4, 3, 5
Solution: Arranging the numbers in ascending order : 0, 1, 1, 2, 2, 3, 3, 3, 4, 5 Here, n = 10 which is even Median = ½ ( n/2 th term + ((n/2)+1)th term) = ½ (10/2 th term + ((10/2)+1)th term) = ½...
(a) Find the median of the following set of numbers : 9, 0, 2, 8, 5, 3, 5, 4, 1, 5, 2, 7 (1990) (b)For the following set of numbers, find the median: 10, 75, 3, 81, 17, 27, 4, 48, 12, 47, 9, 15.
Solution: (a) Arranging the numbers in ascending order : 0, 1, 2, 2, 3, 4, 5, 5, 5, 7, 8, 9 Here, n = 12 which is even Median = ½ ( n/2 th term + ((n/2)+1)th term) = ½ (12/2 th term +...
A student scored the following marks in 11 questions of a question paper : 3, 4, 7, 2, 5, 6, 1, 8, 2, 5, 7 Find the median marks.
Solution: Arranging the data in the ascending order 1,2,2,3,4,5,5,6,7,7,8 Here number of terms, n = 11 Here n is odd. So median = [(n+1)/2 ]th observation = (11+1)/2 = 12/2 = 6th observation Here...
Using the information given in the adjoining histogram, calculate the mean correct to one decimal place.
Solution: Class mark, xi = (upper class limit + lower class limit)/2 Assumed mean, A = 45 Class interval frequency (fi) Class mark (xi) di = xi – A fidi 20-30 3 25 -20 -60 30-40 5 35 -10 -50 40-50...
The following table gives the life time in days of 100 electricity tubes of a certain make :
Life time in days No. of tubes Less than 50 8 Less than 100 23 Less than 150 55 Less than 200 81 Less than 250 93 Less than 300 100 Find the mean life time of electricity tubes. Solution: Class mark...
The mean of the following frequency distribution is 57.6 and the sum of all the frequencies is 50. Find the values of p and q.
Class intervals 0-20 20-40 40-60 60-80 80-100 100-120 Frequency 7 P 12 q 8 5 Solution: Class mark, xi = (upper class limit + lower class limit)/2 Class intervals Frequency fi Class mark xi fixi 0-20...
The mean of the following distribution is 50 and the sum of all the frequencies is 120. Find the values of p and q.
Class intervals 0-20 20-40 40-60 60-80 80-100 Frequency 17 P 32 q 19 Solution: Class mark, xi = (upper class limit + lower class limit)/2 Class intervals Frequency fi Class mark xi fixi 0-20 17 10...
The following distribution shows the daily pocket allowance for children of a locality. The mean pocket allowance is Rs. 18. Find the value of f.
Daily pocket allowance in Rs. 11-13 13-15 15-17 17-19 19-21 21-23 23-25 No. of children 3 6 9 13 f 5 4 Solution: Class mark, xi = (upper class limit + lower class limit)/2 Daily pocket allowance in...
The mean of the following distribution is 23.4. Find the value of p.
Class intervals 0-8 8-16 16-24 24-32 32-40 40-48 Frequency 5 3 10 P 4 2 Solution: Class mark, xi = (upper class limit + lower class limit)/2 Class intervals Frequency fi Class mark xi fixi 0-8 5 4...
A class teacher has the following absentee record of 40 students of a class for the whole term. Find the mean number of days a student was absent.
No. of days 0-6 6-10 10-14 14-20 20-28 28-38 38-40 No. of students 11 10 7 4 4 3 1 Solution: Class mark, xi = (upper class limit + lower class limit)/2 No. of days Frequency fi Class mark xi fixi...
Calculate the mean of the distribution given below using the short cut method.
Marks 11-20 21-30 31-40 41-50 51-60 61-70 71-80 No. of students 2 6 10 12 9 7 4 Solution: Class mark, xi = (upper class limit + lower class limit)/2 Assumed mean, A = 45.5 Marks No. of students (fi)...
The following table gives the daily wages of workers in a factory:
Wages in Rs. 45-50 50-55 55-60 60-65 65-70 70-75 75-80 No. of workers 5 8 30 25 14 12 6 Calculate their mean by short cut method. Solution: Class mark, xi = (upper class limit + lower class limit)/2...
Calculate the mean of the following distribution using step deviation method:
Marks 0-10 10-20 20-30 30-40 40-50 50-60 No. of students 10 9 25 30 16 10 Solution: Class mark (xi) = (upper limit + lower limit)/2 Let assumed mean (A) = 25 Class size (h) = 10 Class Interval No....
Find the mean of the following distribution.
Class interval 0-10 10-20 20-30 30-40 40-50 Frequency 10 6 8 12 5 Solution: Class mark, xi = (upper class limit + lower class limit)/2 Class interval Frequency fi Class mark xi fixi 0-10 10 5 50...
Find the value of the missing variate for the following distribution whose mean is 10
Variate (xi) 5 7 9 11 _ 15 20 Frequency (fi) 4 4 4 7 3 2 1 Solution: Let the missing variate be x. Variate (xi) Frequency (fi) fixi 5 4 20 7 4 28 9 4 36 11 7 77 x 3 3x 15 2 30 20 1 20 Total Ʃfi =25...
If the mean of the following distribution is 7.5, find the missing frequency ” f “.
Variate 5 6 7 8 9 10 11 12 Frequency 20 17 f 10 8 6 7 6 Solution: Variate (x) Frequency (f) fx 5 20 100 6 17 102 7 f 7f 8 10 80 9 8 72 10 6 60 11 7 77 12 6 72 Total Ʃf = 74+f Ʃfx = 563+7f Given mean...
Six coins were tossed 1000 times, and at each toss the number of heads were counted and the results were recorded as under
No. of heads 6 5 4 3 2 1 0 No. of tosses 20 25 160 283 338 140 34 Calculate the mean for this distribution. Solution: No. of heads (x) No. of tosses (f) fx 6 20 6×20 = 120 5 25 5×25 = 125 4 160...
Calculate the mean for the following distribution :
Pocket money (in Rs) 60 70 80 90 100 110 120 No. of students 2 6 13 22 24 10 3 Solution: Pocket money in Rs (x) Number of students (f) fx 60 2 60×2 = 120 70 6 70×6 = 420 80 13 80×13 = 1040 90 22...
Find the mean of the following distribution:
Number 5 10 15 20 25 30 35 Frequency 1 2 5 6 3 2 1 Solution: Number (x) Frequency (f) fx 5 1 5×1 = 5 10 2 10×2 = 20 15 5 15×5 = 75 20 6 20×6 = 120 25 3 25×3 = 75 30 2 30×2 = 60 35 1 35×1 = 35 Total...
Using ruler and compasses only, draw an equilateral triangle of side 5 cm and draw its inscribed circle. Measure the radius of the circle.
Solution: Steps to construct: Step 1: Draw a line segment BC = 5cm. Step 2: With Center as B and radius 5cm, with center as C and radius 5cm draw two arcs which intersect each other at point A. Step...
Construct a tangent to a circle of radius 4cm from a point on the concentric circle of radius 6 cm and measure its length. Also, verify the measurement by actual calculation.
Solution: Steps to construct: Step 1: Mark a point O. Step 2: With center O and radius 4cm and 6cm, draw two concentric circles. Step 3: Join OA and mark its mid-point as M. Step 4: With center M...
(a) If a, b, c are the sides of a right triangle where c is the hypotenuse, prove that the radius r of the circle which touches the sides of the triangle is given by r = /frac (a + b – c) – (2) (b) In the given figure, PB is a tangent to a circle with center O at B. AB is a chord of length 24 cm at a distance of 5 cm from the center. If the length of the tangent is 20 cm, find the length of OP.
Solution: (a) Let the circle touch the sides BC, CA and AB of the right triangle ABC at points D, E and F respectively, where BC = a, CA = b and AB = c (as showing in the given figure). As the...
The tangent to a circle of radius 6 cm from an external point P, is of length 8 cm. Calculate the distance of P from the nearest point of the circle.
Solution: Radius of the circle = 6 cm and length of tangent = 8 cm Let OP be the distance i.e. OA = 6 cm, AP = 8 cm . OA is the radius OA ⊥ AP Now In right ∆OAP, OP2 = OA2 + AP2 (By Pythagoras...
A point P is at a distance 13 cm from the center C of a circle and PT is a tangent to the given circle. If PT = 12 cm, find the radius of the circle.
Solution: CT is the radius CP = 13 cm and tangent PT = 12 cm CT is the radius and TP is the tangent CT is perpendicular TP Now in right angled triangle CPT, CP2 = CT2 + PT2 [using Pythagoras axiom]...
(a) In the figure given below, O is the center of the circle. If ∠BAD = 30°, find the values of p, q and r.
(a) In the figure given below, two circles intersect at points P and Q. If ∠A = 80° and ∠D = 84°, calculate (i) ∠QBC (ii) ∠BCP Solution: (i) ABCD is a cyclic quadrilateral ∠A + ∠C = 180o 30o + p =...
(a) In the figure (i) given below, O is the center of the circle. If ∠AOC = 150°, find (i) ∠ABC (ii) ∠ADC (b) In the figure (i) given below, AC is a diameter of the given circle and ∠BCD = 75°. Calculate the size of (i) ∠ABC (ii) ∠EAF.
Solution: (a) Given, ∠AOC = 150° and AD = CD We know that an angle subtends by an arc of a circle at the center is twice the angle subtended by the same arc at any point on the remaining part of the...
(a) In the figure (i) given below, AB is a diameter of the circle APBR. APQ and RBQ are straight lines, ∠A = 35°, ∠Q = 25°. Find (i) ∠PRB (ii) ∠PBR (iii) ∠BPR. (b) In the figure (ii) given below, it is given that ∠ABC = 40° and AD is a diameter of the circle. Calculate ∠DAC.
Solution (a) (i) ∠PRB = ∠BAP (Angles in the same segment of the circle) ∴ ∠PRB = 35° (∵ ∠BAP = 35° given)
(a) In the figure (i) given below, M, A, B, N are points on a circle having centre O. AN and MB cut at Y. If ∠NYB = 50° and ∠YNB = 20°, find ∠MAN and the reflex angle MON. (b) In the figure (ii) given below, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°, find (i) ∠ACB (ii) ∠OBC (iii) ∠OAB (iv) ∠CBA
Solution (a) ∠NYB = 50°, ∠YNB = 20°. In ∆YNB, ∠NYB + ∠YNB + ∠YBN = 180o 50o + 20o + ∠YBN = 180o ∠YBN + 70o = 180o ∠YBN = 180o – 70o = 110o But ∠MAN = ∠YBN (Angles in the same segment) ∠MAN = 110o...
In the figure (i) given below, calculate the values of x and y. (b) In the figure (ii) given below, O is the centre of the circle. Calculate the values of x and y.
(a) ABCD is cyclic Quadrilateral ∠B + ∠D = 1800 Y + 400 + 45o = 180o (y + 85o = 180o) Y = 180o – 85o = 95o ∠ACB = ∠ADB xo = 40 (a) Arc ADC Subtends ∠AOC at the centre and ∠ ABC at the remaining part...
Solve 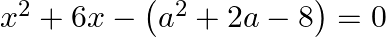
$\begin{array}{l} x^{2}+6 x-\left(a^{2}+2 a-8\right)=0 \\ \Rightarrow x^{2}+6 x-(a+4)(a-2)=0 \\ \Rightarrow x^{2}+[(a+4)-(a-2)] x-(a+4)(a-2)=0 \\ \Rightarrow x^{2}+(a+4) x-(a-2) x-(a+4)(a-2)=0 \\...
Solve 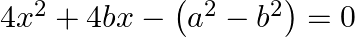
$\begin{array}{l} 4 x^{2}+4 b x-\left(a^{2}-b^{2}\right)=0 \\ \Rightarrow 4 x^{2}+4 b x-(a-b)(a+b)=0 \\ \Rightarrow 4 x^{2}+2[(a+b)-(a-b)] x-(a-b)(a+b)=0 \\ \Rightarrow 4 x^{2}+2(a+b) x-2(a-b)...
Solve 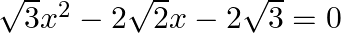
$\begin{array}{l} \sqrt{3} x^{2}-2 \sqrt{2} x-2 \sqrt{3}=0 \\ \Rightarrow \sqrt{3} x^{2}-3 \sqrt{2} x+\sqrt{2} x-2 \sqrt{3}=0 \\ \Rightarrow \sqrt{3} x(x-\sqrt{6})+\sqrt{2}(x-\sqrt{6})=0 \\...
Solve 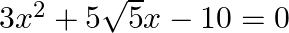
$\begin{array}{l} 3 x^{2}+5 \sqrt{5} x-10=0 \\ \Rightarrow 3 x^{2}+6 \sqrt{5} x-\sqrt{5} x-10=0 \\ \Rightarrow 3 x(x+2 \sqrt{5})-\sqrt{5}(x+2 \sqrt{5})=0 \\ \Rightarrow(x+2 \sqrt{5})(3 x-\sqrt{5})=0...
Solve 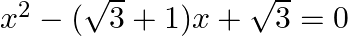
$\begin{array}{l} x^{2}-(\sqrt{3}+1) x+\sqrt{3}=0 \\ \Rightarrow x^{2}-\sqrt{3} x-x+\sqrt{3}=0 \\ \Rightarrow x(x-\sqrt{3})-1(x-\sqrt{3})=0 \\ \Rightarrow(x-\sqrt{3})(x-1)=0 \\ \Rightarrow...
Find the value of  for which the quadratic equation
for which the quadratic equation 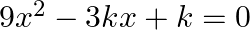 has equal roots.
has equal roots.
It is given that the quadratic equation $9 x^{2}-3 k x+k=0$ has equal roots. $\begin{array}{l} \therefore D=0 \\ \Rightarrow(-3 k)^{2}-4 \times 9 \times k=0 \\ \Rightarrow 9 k^{2}-36 k=0 \\...
If the roots of the quadratic equation 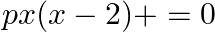 are equal, find the value of
are equal, find the value of 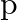 .
.
It is given that the roots of the quadratic equation $p x^{2}-2 p x+6=0$ are equal. $\begin{array}{l} \therefore D=0 \\ \Rightarrow(-2 p)^{2}-4 \times p \times 6=0 \\ \Rightarrow 4 p^{2}-24 p=0 \\...
If one zero of the polynomial 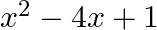 is
is 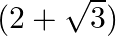 , write the other zero.
, write the other zero.
Let the other zero of the given polynomial be $\alpha$. Now, Sum of the zeroes of the given polynomial $=\frac{-(-4)}{1}=4$ $\begin{array}{l} \therefore \alpha+(2+\sqrt{3})=4 \\ \Rightarrow...
If the quadratic equation 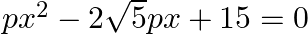 has two equal roots then find the value of
has two equal roots then find the value of 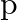 .
.
It is given that the quadratic equation $p x^{2}-2 \sqrt{5} p x+15=0$ has two equal roots. $\begin{array}{l} \therefore D=0 \\ \Rightarrow(-2 \sqrt{5} p)^{2}-4 \times p \times 15=0 \\ \Rightarrow 20...
Find the solution of the quadratic equation 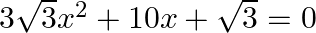 .
.
The given quadratic equation is $3 \sqrt{3} x^{2}+10 x+\sqrt{3}=0$ $\begin{array}{l} 3 \sqrt{3} x^{2}+10 x+\sqrt{3}=0 \\ \Rightarrow 3 \sqrt{3} x^{2}+9 x+x+\sqrt{3}=0 \\ \Rightarrow 3 \sqrt{3}...
Find the roots of the quadratic equation 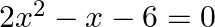 .
.
The given quadratic equation is $2 x^{2}-x-6=0$ $\begin{array}{l} 2 x^{2}-x-6=0 \\ \Rightarrow 2 x^{2}-4 x+3 x-6=0 \\ \Rightarrow 2 x(x-2)+3(x-2)=0 \\ \Rightarrow(x-2)(2 x+3)=0 \\ \Rightarrow x-2=0...
Show that 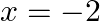 is a solution of
is a solution of 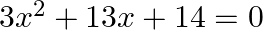 .
.
The given equation is $3 x^{2}+13 x+14=0$. Putting $x=-2$ in the given equation, we get $L H S-3 \times(-2)^{2}+13 \times(-2)+14=12-26+14=0=R H S$ $\therefore x=-2$ is a solution of the given...
The roots of the quadratic equation 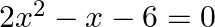 . are
. are
(a) 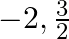
(b) 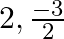
(c) 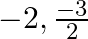
(d) 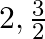
Answer is (b) $2, \frac{-3}{2}$ The given quadratic equation is $2 x^{2}-x-6=0$. $\begin{array}{l} 2 x^{2}-x-6=0 \\ \Rightarrow 2 x^{2}-4 x+3 x-6=0 \\ \Rightarrow 2 x(x-2)+3(x-2)=0 \\...
If the equation 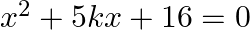 has no real roots then
has no real roots then
(a) 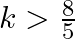
(b) 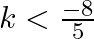
(c) 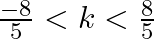
(d) None of these
Answer is (c) $\frac{-8}{5}<k<\frac{8}{5}$ It is given that the equation $\left(x^{2}+5 k x+16=0\right)$ has no real roots. $\begin{array}{l} \therefore\left(b^{2}-4 a c\right)<0 \\...
In the equation 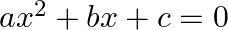 , it is given that
, it is given that 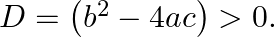 Then, the roots of the equation are
Then, the roots of the equation are
(a) real and equal
(b) real and unequal
(c) imaginary
(d) none of these
Answer is (b) real and unequal We know that when discriminant, $D>0$, the roots of the given quadratic cquation are real and uncqual.
If the equation 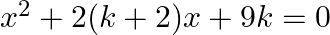 has equal roots then
has equal roots then 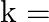 ?
?
(a) 1 or 4
(b)-1 or 4
(c) 1 or -4
(d) -1 or -4
Answer is (a) 1 or 4 It is given that the roots of the equation $\left(x^{2}+2(k+2) x+9 k=0\right)$ are equal. $\begin{array}{l} \therefore\left(b^{2}-4 a c\right)=0 \\ \Rightarrow\{2(k+2)\}^{2}-4...
If the roots of the equation 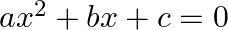 are equal then
are equal then 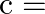 ?
?
(a) 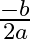
(b) 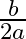
(c) 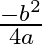
(d) 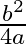
Answer is (d) $\frac{b^{2}}{4 a}$ It is given that the roots of the equation $\left(a x^{2}+b x+c=0\right)$ are equal. $\begin{array}{l} \therefore\left(b^{2}-4 a c\right)=0 \\ \Rightarrow b^{2}=4 a...
If 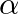 and
and 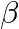 are the roots of the equation
are the roots of the equation 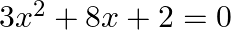 then
then 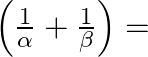 ?
?
(a) 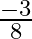
(b) 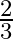
(c) 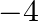
(d) 4
Answer is (c) $-4$ It is given that $\alpha$ and $\beta$ are the roots of the equation $3 x^{2}+8 x+2=0$ $\therefore \alpha+\beta=-\frac{8}{3}$ and $\alpha \beta=\frac{2}{3}$...
If the sum of the roots of the equation 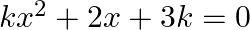 is equal to their product then the value of
is equal to their product then the value of 
(a) 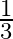
(b) 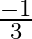
(c) 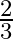
(d) 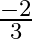
Answer is (d) $\frac{-2}{3}$ Given: $k x^{2}+2 x+3 k=0$ Sum of the roots $=$ Product of the roots $\begin{array}{l} \Rightarrow \frac{-2}{k}=\frac{3 k}{k} \\ \Rightarrow 3 k=-2 \\ \Rightarrow...
The ratio of the sum and product of the roots of the equation 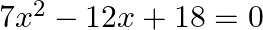 is
is
(a) 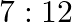
(b) 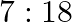
(c) 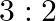
(d) 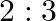
Answer is (d) $2: 3$ Given: $7 x^{2}-12 x+18=0$ $\therefore \alpha+\beta=\frac{12}{7}$ and $\beta=\frac{18}{7}$, where $\alpha$ and $\beta$ are the roots of the equation $\therefore$ Ratio of the...
The sum of the roots of the equation 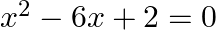 is
is
(a) 2
(b) 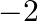
(c) 6
(d) 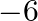
Answer is (b) -2 Sum of the roots of the equation $x^{2}-6 x+2=0$ is $\alpha+\beta=\frac{-b}{a}=\frac{-(-6)}{1}=6$, where $\alpha$ and $\beta$ are the roots of the equation.
If 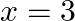 is a solution of the equation
is a solution of the equation 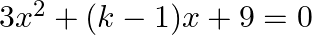 , then
, then 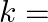 ?
?
(a) 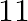
(b) 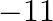
(c) 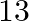
(d) 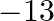
Answer is (b) $-11$ It is given that $x=3$ is a solution of $3 x^{2}+(k-1) x+9=0$; therefore, we have: $\begin{array}{l} 3(3)^{2}+(k-1) \times 3+9=0 \\ \Rightarrow 27+3(k-1)+9=0 \\ \Rightarrow...
Which of the following is not a quadratic equation?
(a) 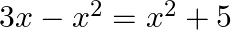
(b) 
(c) 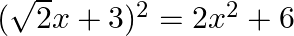
(d) 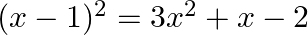
Answer is (c) $(\sqrt{2} x+3)^{2}=2 x^{2}+6$ $\begin{array}{l} \because(\sqrt{2} x+3)^{2}=2 x^{2}+6 \\ \Rightarrow 2 x^{2}+9+6 \sqrt{2} x=2 x^{2}+6 \end{array}$ $\Rightarrow 6 \sqrt{2} x+3=0$, which...
The hypotenuse of a right-angled triangle is 1 meter less than twice the shortest side. If the third side 1 meter more than the shortest side, find the side, find the sides of the triangle.
Let the shortest side be $x \mathrm{~m}$. Therefore, according to the question: Hypotenuse $=(2 x-1) m$ Third side $=(x+1) m$ On applying Pythagoras theorem, we get: $\begin{array}{l} (2...
The hypotenuse of a right-angled triangle is 20 meters. If the difference between the lengths of the other sides be 4 meters, find the other sides
Let one side of the right-angled triangle be $x \mathrm{~m}$ and the other side be $(x+4) \mathrm{m}$. On applying Pythagoras theorem, we have: $\begin{array}{l} 20^{2}=(x+4)^{2}+x^{2} \\...
The area of right-angled triangle is 96 sq meters. If the base is three time the altitude, find the base.
Let the altitude of the triangle be $x \mathrm{~m}$. Therefore, the base will be $3 x \mathrm{~m}$. $\begin{array}{l} \text { Area of a triangle }=\frac{1}{2} \times \text { Base } \times \text {...
A farmer prepares rectangular vegetable garden of area 180 sq meters. With 39 meters of barbed wire, he can fence the three sides of the garden, leaving one of the longer sides unfenced. Find the dimensions of the garden.
Let the length and breadth of the rectangular garden be $x$ and $y$ meter, respectively. Given: $x y=180 \mathrm{sq} \mathrm{m}$$\ldots(i)$ and $\begin{array}{l} 2 y+x=39 \\ \Rightarrow x=39-2 y...
The sum of the areas of two squares is 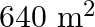 . If the difference in their perimeter be
. If the difference in their perimeter be 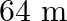 , find the sides of the two square
, find the sides of the two square
Let the length of the side of the first and the second square be $x$ and $y \cdot$ respectively. According to the question: $x^{2}+y^{2}=640$ Also, $\begin{array}{l} 4 x-4 y=64 \\ \Rightarrow x-y=16...
The perimeter of a rectangular plot is  and its area is 288 sq meters. Find the dimension of the plot
and its area is 288 sq meters. Find the dimension of the plot
Let the length and breadth of the rectangular plot be $x$ and $y$ meter, respectively. Therefore, we have: $\begin{array}{l} \text { Perimeter }=2(x+y)=62 \quad \ldots . .(i) \text { and } \\ \text...
The length of a hall is 3 meter more than its breadth. If the area of the hall is 238 sq meters, calculate its length and breadth.
Let the breath of the rectangular hall be $x$ meter. Therefore, the length of the rectangular hall will be $(x+3)$ meter. According to the question: $\begin{array}{l} x(x+3)=238 \\ \Rightarrow...
Two water taps together can fill a tank in 6 hours. The tap of larger diameter takes 9 hours less than the smaller one to fill the tank separately. Find the time which each tap can separately fill the tank.
Let the tap of smaller diameter fill the tank in $x$ hours. $\therefore$ Time taken by the tap of larger diameter to fill the tank $=(x-9) h$ Suppose the volume of the tank be $V$. Volume of the...
Two pipes running together can fill a cistern in 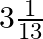 minutes. If one pipe takes 3 minutes more than the other to fill it, find the time in which each pipe would fill the cistern.
minutes. If one pipe takes 3 minutes more than the other to fill it, find the time in which each pipe would fill the cistern.
Let one pipe fills the cistern in $x$ mins. Therefore, the other pipe will fill the cistern in $(x+3)$ mins. Time taken by both, running together, to fill the cistern $=3 \frac{1}{13} \min...
A motorboat whose speed is 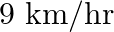 in still water, goes
in still water, goes 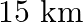 downstream and comes back in a total time of 3 hours 45 minutes. Find the speed of the stream.
downstream and comes back in a total time of 3 hours 45 minutes. Find the speed of the stream.
Let the speed of the stream be $x \mathrm{~km} / \mathrm{hr}$. $\therefore$ Downstream speed $=(9+x) \mathrm{km} / \mathrm{hr}$ Upstream speed $=(9-x) \mathrm{km} / \mathrm{hr}$ Distance covered...
A motor boat whose speed in still water is 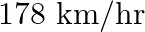 , takes 1 hour more to go
, takes 1 hour more to go 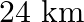 upstream than to return to the same spot. Find the speed of the stream.
upstream than to return to the same spot. Find the speed of the stream.
Let the speed of the stream be $x \mathrm{~km} / \mathrm{hr}$. Given: Speed of the boat $=18 \mathrm{~km} / \mathrm{hr}$ $\therefore$ Speed downstream $=(18+x) \mathrm{km} / h r$ Speed upstream...
A train covers a distance of 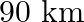 at a uniform speed. Had the speed been
at a uniform speed. Had the speed been 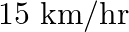 more, it would have taken 30 minutes less for the journey. Find the original speed of the train.
more, it would have taken 30 minutes less for the journey. Find the original speed of the train.
Let the original speed of the train be $x \mathrm{~km} / \mathrm{hr}$. According to the question: $\frac{90}{x}-\frac{90}{(x+15)}=\frac{1}{2}$ $\begin{array}{l} \Rightarrow \frac{90(x+15)-90...
A train travels at a certain average speed for a distanced of 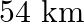 and then travels a distance of 63
and then travels a distance of 63 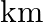 at an average speed of
at an average speed of 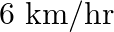 more than the first speed. If it takes 3 hours to complete the total journey, what is its first speed?
more than the first speed. If it takes 3 hours to complete the total journey, what is its first speed?
Let the first speed of the train be $x \mathrm{~km} / \mathrm{h}$. Time taken to cover $54 \mathrm{~km}=\frac{54}{x} h .$ New speed of the train $=(x+6) \mathrm{km} / \mathrm{h}$ $\therefore$ Time...
A train covers a distance of 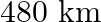 at a uniform speed. If the speed had been
at a uniform speed. If the speed had been 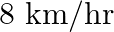 less then it would have taken 3 hours more to cover the same distance. Find the usual speed of the train.
less then it would have taken 3 hours more to cover the same distance. Find the usual speed of the train.
Let the usual speed of the train be $x \mathrm{~km} / \mathrm{h}$. $\therefore$ Reduced speed of the train $=(x-8) \mathrm{km} / \mathrm{h}$ Total distance to be covered $=480 \mathrm{~km}$ Time...
Find the domain and range of the relation
R = {(-1, 1), (1, 1), (-2, 4), (2, 4)}.
Solution: Set of all the first elements or $x$-coordinates of the ordered pairs is called Domain. Set of all the second elements or $y$-coordinates of the ordered pairs is called Range. Therefore,...
If a, b, c and d are in proportion, prove that: (iii) ![Rendered by QuickLaTeX.com \[({{\mathbf{a}}^{\mathbf{4}}}~+\text{ }{{\mathbf{c}}^{\mathbf{4}}}):\text{ }({{\mathbf{b}}^{\mathbf{4}}}~+\text{ }{{\mathbf{d}}^{\mathbf{4}}})\text{ }=\text{ }{{\mathbf{a}}^{\mathbf{2}}}{{\mathbf{c}}^{\mathbf{2}}}:\text{ }{{\mathbf{b}}^{\mathbf{2}}}{{\mathbf{d}}^{\mathbf{2}}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-faf03a20682e0b4ba6b313808f983f5f_l3.png)
(iv) ![Rendered by QuickLaTeX.com \[\frac{{{a}^{2}}+ab}{{{c}^{2}}+cd}=\frac{{{b}^{2}}-2ab}{{{d}^{2}}-2cd}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d6ef2f46a5b3995094cfb48fc5acf92f_l3.png)
![Rendered by QuickLaTeX.com \[\frac{{{a}^{2}}+ab}{{{c}^{2}}+cd}=\frac{{{b}^{2}}-2ab}{{{d}^{2}}-2cd}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d6ef2f46a5b3995094cfb48fc5acf92f_l3.png)
It is given that a, b, c, d are in proportion Consider a/b = c/d = k a = b, c = dk (iii) \[({{a}^{4}}~+\text{ }{{c}^{4}}):\text{ }({{b}^{4}}~+\text{ }{{d}^{4}})\text{ }=\text{...
If one root of the equation 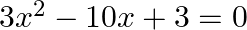 is
is 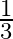 then the other root is
then the other root is
(a) 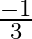
(b) 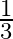
(c) -3
(d) 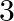
Answer is (d)3 Given: $3 x^{2}-10 x+3=0$ One root of the equation is $\frac{1}{3}$. Let the other root be $\alpha$. Product of the roots $=\frac{c}{a}$ $\begin{array}{l} \Rightarrow \frac{1}{3}...
If the product of the roots of the equation 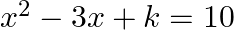 is
is 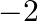 then the value of
then the value of 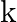 is
is
(a) 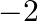
(b) 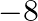
(c) 8
(d) 12
Answer is (c) 8 It is given that the product of the roots of the equation $x^{2}-3 x+k=10$ is $-2$. The equation can be rewritten as: $x^{2}-3 x+(k-10)=0$ Product of the roots of a quadratic...
If one root of the equation 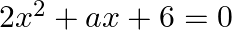 is 2 then
is 2 then 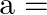 ?
?
(a) 7
(b) 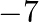
(c) 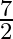
(d) 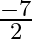
Answer is (b) $-7$ It is given that one root of the equation $2 x^{2}+a x+6=0$ is 2 . $\begin{array}{l} \therefore 2 \times 2^{2}+a \times 2+6=0 \\ \Rightarrow 2 a+14=0 \\ \Rightarrow a=-7...
Which of the following is not a quadratic equation?
(a) 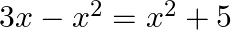
(b) 
(c) 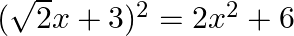
(d) 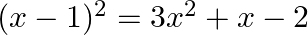
Answer is (c) $(\sqrt{2} x+3)^{2}=2 x^{2}+6$ $\begin{array}{l} \because(\sqrt{2} x+3)^{2}=2 x^{2}+6 \\ \Rightarrow 2 x^{2}+9+6 \sqrt{2} x=2 x^{2}+6 \end{array}$ $\Rightarrow 6 \sqrt{2} x+3=0$, which...
The area of right -angled triangle is 165 sq meters. Determine its base and altitude if the latter exceeds the former by 7 meters.
Let the base be $x \mathrm{~m}$. Therefore, the altitude will be $(x+7) m$. Area of a triangle $=\frac{1}{2} \times$ Base $\times$ Altitude $\begin{array}{l} \therefore \frac{1}{2} \times x...
The area of a right triangle is 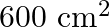 . If the base of the triangle exceeds the altitude by
. If the base of the triangle exceeds the altitude by 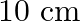 , find the dimensions of the triangle.
, find the dimensions of the triangle.
Let the altitude of the triangle be $x \mathrm{~cm}$ Therefore, the base of the triangle will be $(x+10) \mathrm{cm}$ $\begin{array}{l} \text { Area of triangle }=\frac{1}{2} x(x+10)=600 \\...
The length of a rectangle is thrice as long as the side of a square. The side of the square is 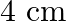 more than the width of the rectangle. Their areas being equal, find the dimensions.
more than the width of the rectangle. Their areas being equal, find the dimensions.
Let the breadth of rectangle be $x \mathrm{~cm}$. According to the question: Side of the square $=(x+4) \mathrm{cm}$ Length of the rectangle $=\{3(x+4)\} \mathrm{cm}$ It is given that the areas of...
A rectangular filed in 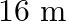 long and
long and 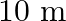 wide. There is a path of uniform width all around it, having an area of
wide. There is a path of uniform width all around it, having an area of 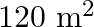 . Find the width of the path
. Find the width of the path
Let the width of the path be $x \mathrm{~m}$. $\therefore$ Length of the field including the path $=16+x+x=16+2 x$ Breadth of the field including the path $=10+x+x=10+2 x$ Now, (Area of the field...
The length of a hall is 3 meter more than its breadth. If the area of the hall is 238 sq meters, calculate its length and breadth.
Let the breath of the rectangular hall be $x$ meter. Therefore, the length of the rectangular hall will be $(x+3)$ meter. According to the question: $\begin{array}{l} x(x+3)=238 \\ \Rightarrow...
The length of rectangle is twice its breadth and its areas is 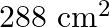 . Find the dimension of the rectangle.
. Find the dimension of the rectangle.
Let the length and breadth of the rectangle be $2 x \mathrm{~m}$ and $x \mathrm{~m}$, respectively. According to the question: $2 x \times x=288$ $\Rightarrow 2 x^{2}=288$ $\Rightarrow x^{2}=144$...
Two pipes running together can fill a tank in 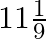 minutes. If on pipe takes 5 minutes more than the other to fill the tank separately, find the time in which each pipe would fill the tank separately.
minutes. If on pipe takes 5 minutes more than the other to fill the tank separately, find the time in which each pipe would fill the tank separately.
Let the time taken by one pipe to fill the tank be $x$ minutes. $\therefore$ Time taken by the other pipe to fill the tank $=(x+5) \min$ Suppose the volume of the tank be $V$. Volume of the tank...
A takes 10 days less than the time taken by  to finish a piece of work. If both
to finish a piece of work. If both  and
and  together can finish the work in 12 days, find the time taken by
together can finish the work in 12 days, find the time taken by  to finish the work.
to finish the work.
Let B takes $x$ days to complete the work. Therefore, A will take $(x-10)$ days. $\begin{array}{l} \therefore \frac{1}{x}+\frac{1}{(x-10)}=\frac{1}{12} \\ \Rightarrow...
The speed of a boat in still water is 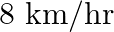 . It can go
. It can go 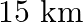 upstream and
upstream and 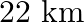 downstream is 5 hours. Fid the speed of the stream
downstream is 5 hours. Fid the speed of the stream
Speed of the boat in still water $=8 \mathrm{~km} / \mathrm{hr}$. Let the speed of the stream be $x \mathrm{~km} / \mathrm{hr}$. $\therefore$ Speed upstream $=(8-x) \mathrm{km} / \mathrm{hr}$ Speed...
The distance between Mumbai and Pune is 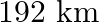 . Travelling by the Deccan Queen, it takes 48 minutes less than another train. Calculate the speed of the Deccan Queen if the speeds of the two train differ by
. Travelling by the Deccan Queen, it takes 48 minutes less than another train. Calculate the speed of the Deccan Queen if the speeds of the two train differ by 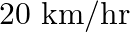 .
.
Let the speed of the Deccan Queen be $x \mathrm{~km} / \mathrm{hr}$. According to the question: Speed of another train $=(x-20) \mathrm{km} / \mathrm{hr}$ $\begin{array}{l} \therefore...
A train covers a distance of 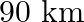 at a uniform speed. Had the speed been
at a uniform speed. Had the speed been 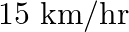 more, it would have taken 30 minutes less for the journey. Find the original speed of the train.
more, it would have taken 30 minutes less for the journey. Find the original speed of the train.
Let the original speed of the train be $x \mathrm{~km} / \mathrm{hr}$. According to the question: $\frac{90}{x}-\frac{90}{(x+15)}=\frac{1}{2}$ $\begin{array}{l} \Rightarrow \frac{90(x+15)-90...
While boarding an aeroplane, a passengers got hurt. The pilot showing promptness and concern, made arrangements to hospitalize the injured and so the plane started late by 30 minutes. To reach the destination, 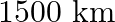 away, in time, the pilot increased the speed by
away, in time, the pilot increased the speed by 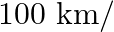 hour. Find the original speed of the plane. Do you appreciate the values shown by the pilot, namely promptness in providing help to the injured and his efforts to reach in time?
hour. Find the original speed of the plane. Do you appreciate the values shown by the pilot, namely promptness in providing help to the injured and his efforts to reach in time?
Let the original speed of the plane be $x \mathrm{~km} / \mathrm{h}$. $\therefore$ Actual speed of the plane $=(x+100) \mathrm{km} / \mathrm{h}$ Distance of the journey $=1500 \mathrm{~km}$ Time...
The sum of the ages of a boy and his brother is 25 years, and the product of their ages in years is 126 . Find their ages.
Let the present ages of the boy and his brother be $x$ years and $(25-x)$ years. According to the question: $\begin{array}{l} x(25-x)=126 \\ \Rightarrow 25 x-x^{2}=126 \\ \Rightarrow x^{2}-(18-7)...
One year ago, man was 8 times as old as his son. Now, his age is equal to the square of his son’s age. Find their present ages.
Let the present age of the son be $x$ years. $\therefore$ Present age of the $\operatorname{man}=x^{2}$ years One year ago, Age of the son $=(x-1)$ years Age of the man $=\left(x^{2}-1\right)$ years...
A man buys a number of pens for Rs. 180 . If he had bought 3 more pens for the same amount, each pen would have cost him Rs. 3 less. How many pens did he buy?
Let the total number of pens be $x$. According to the question: $\begin{array}{l} \frac{80}{x}-\frac{80}{x+4}=1 \\ \Rightarrow \frac{80(x+4)-80 x}{x(x+4)}=1 \\ \Rightarrow \frac{80+320-80 x}{x^{2}+4...
A person on tour has Rs. 10800 for his expenses. If he extends his tour by 4 days, he has to cut down his daily expenses by Rs. 90 . Find the original duration of the tour.
Let the original duration of the tour be $x$ days. $\therefore \text { Original daily expenses }=\text { γ } \frac{10,800}{x}$ If he extends his tour by 4 days, then his new daily expenses...
The numerator of a fraction is 3 less than its denominator. If 1 is added to the denominator, the fraction is decreased by 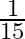 . Find the fraction.
. Find the fraction.
Let the denominator of the required fraction be $x$. Numerator of the required fraction $=x-3$ $\therefore$ Original fraction $=\frac{x-3}{x}$ If 1 is added to the denominator, then the new fraction...
A two-digit number is such that the product of its digits is 14 . If 45 is added to the number, the digit interchange their places. Find the number.
Let the digits at units and tens places be $x$ and $y$, respectively. $\therefore x y=14$ $\Rightarrow y=\frac{14}{x}$ According to the question: $\begin{array}{l} (10 y+x)+45=10 x+y \\ \Rightarrow...
Three consecutive positive integers are such that the sum of the square of the first and product of the other two is 46 . Find the integers.
Let the three consecutive positive integers be $x, x+1$ and $x+2$. According to the given condition, $\begin{array}{l} x^{2}+(x+1)(x+2)=46 \\ \Rightarrow x^{2}+x^{2}+3 x+2=46 \\ \Rightarrow 2...
Divide two natural numbers, the sum of whose squares is 25 times their sum and also equal to 50 times their difference.
Let the two natural numbers be $x$ and $y$. According to the question: $\begin{array}{l} x^{2}+y^{2}=25(x+y) \quad \ldots \ldots(i) \\ x^{2}+y^{2}=50(x-y) \end{array}$ From (i) and (ii), we get:...
Divide 27 into two parts such that the sum of their reciprocal is 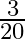 .
.
Let the two parts be $x$ and $(27-x)$. According to the given condition, $\begin{array}{l} \frac{1}{x}+\frac{1}{27-x}=\frac{3}{20} \\ \Rightarrow \frac{27-x+x}{x(27-x)}=\frac{3}{20} \\ \Rightarrow...
The sum of natural number and its reciprocal is 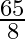 . Find the number.
. Find the number.
Let the natural number be $x$. According to the given condition, $\begin{array}{l} x+\frac{1}{x}=\frac{65}{8} \\ \Rightarrow \frac{x^{2}+1}{x}=\frac{65}{8} \\ \Rightarrow 8 x^{2}+8=65 x \\...
The difference of two natural numbers is 5 and the difference of heir reciprocals is 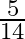 . Find the numbers.
. Find the numbers.
Let the required natural numbers be $x$ and $(x+5)$. Now, $x<x+5$ $\therefore \frac{1}{x}>\frac{1}{x+5}$ According to the given condition, $\begin{array}{l}...
The sum of two natural numbers is 15 and the sum of their reciprocals is 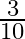 . Find the numbers.
. Find the numbers.
Let the required natural numbers be $x$ and $(15-x)$. According to the given condition, $\begin{array}{l} \frac{1}{x}+\frac{1}{15-x}=\frac{3}{10} \\ \Rightarrow \frac{15-x+x}{x(15-x)}=\frac{3}{10}...
Find the two consecutive positive even integers whose product is 288.
Let the two consecutive positive even integers be $x$ and $(x+2)$. According to the given condition, $\begin{array}{l} x(x+2)=288 \\ \Rightarrow x^{2}+2 x-288=0 \\ \Rightarrow x^{2}+18 x-16 x-288=0...
Find two consecutive multiples of 3 whose product is 648.
Let the required consecutive multiples of 3 be $3 x$ and $3(x+1)$. According to the given condition, $\begin{array}{l} 3 x \times 3(x+1)=648 \\ \Rightarrow 9\left(x^{2}+x\right)=648 \\ \Rightarrow...
The product of two consecutive positive integers is 306 . Find the integers.
Let the two consecutive positive integers be $x$ and $(x+1)$. According to the given condition, $\begin{array}{l} x(x+1)=306 \\ \Rightarrow x^{2}+x-306=0 \\ \Rightarrow x^{2}+18 x-17 x-306=0 \\...
The sum of the squares to two consecutive positive odd numbers is 514 . Find the numbers.
Let the two consecutive positive odd numbers be $x$ and $(x+2)$. According to the given condition, $\begin{array}{l} x^{2}+(x+2)^{2}=514 \\ \Rightarrow x^{2}+x^{2}+4 x+4=514 \\ \Rightarrow 2 x^{2}+4...
The sum of two natural number is 28 and their product is 192 . Find the numbers.
Let the required number be $x$ and $(28-x)$. According to the given condition, $\begin{array}{l} x(28-x)=192 \\ \Rightarrow 28 x-x^{2}=192 \\ \Rightarrow x^{2}-28 x+192=0 \\ \Rightarrow x^{2}-16...
The sum of natural number and its positive square root is 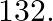 Find the number.
Find the number.
Let the required natural number be $x$. According to the given condition, $x+\sqrt{x}=132$ Putting $\sqrt{x}=y$ or $x=y^{2}$, we get $y^{2}+y=132$ $\Rightarrow y^{2}+y-132=0$ $\Rightarrow y^{2}+12...
If the roots of the equations 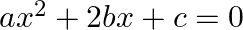 and
and 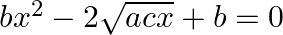 are simultaneously real then prove that
are simultaneously real then prove that 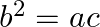
It is given that the roots of the equation $a x^{2}+2 b x+c=0$ are real. $\begin{array}{l} \therefore D_{1}=(2 b)^{2}-4 \times a \times c \geq 0 \\ \Rightarrow 4\left(b^{2}-a c\right) \geq 0 \\...
Find the value of  for which the roots of
for which the roots of 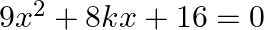 are real and equal
are real and equal
Given: $\begin{array}{l} 9 x^{2}+8 k x+16=0 \\ \text { Here, } \\ a=9, b=8 k \text { and } c=16 \end{array}$ It is given that the roots of the equation are real and equal; therefore, we have:...
Find the value of 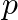 for which the quadratic equation
for which the quadratic equation 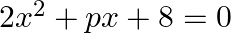 has real roots.
has real roots.
$2 x^{2}+p x+8=0$ Here, $a=2, b=p$ and $c=8$ Discriminant $D$ is given by: $\begin{array}{l} D=\left(b^{2}-4 a c\right) \\ =p^{2}-4 \times 2 \times 8 \\ =\left(p^{2}-64\right) \end{array}$ If $D...
If 3 is a root of the quadratic equation 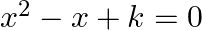 ., find the value of
., find the value of 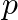 so that the roots of the equation
so that the roots of the equation  are equal.
are equal.
It is given that 3 is a root of the quadratic equation $x^{2}-x+k=0$. $\begin{array}{l} \therefore(3)^{2}-3+k=0 \\ \Rightarrow k+6=0 \\ \Rightarrow k=-6 \end{array}$ The roots of the equation...
Find the values of 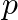 for which the quadratic equation
for which the quadratic equation 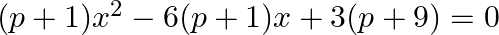 . ,
. , 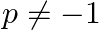 has equal roots. Hence find the roots of the equation.
has equal roots. Hence find the roots of the equation.
The given equation is $(p+1) x^{2}-6(p+1) x+3(p+9)=0$. This is of the form $a x^{2}+b x+c=0$, where $a=p+1, b=-6(p+1)$ and $c=3(p+9)$. $\begin{array}{l} \therefore D=b^{2}-4 a c \\ =[-6(p+1)]^{2}-4...
Find the values of 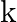 for which the quadratic equation
for which the quadratic equation 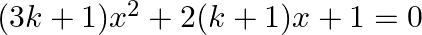 . has real and equal roots.
. has real and equal roots.
The given equation is $(3 k+1) x^{2}+2(k+1) x+1=0$. This is of the form $a x^{2}+b x+c=0$, where $a=3 k+1, b=2(k+1)$ and $c=1$. $\begin{array}{l} \therefore D=b^{2}-4 a c \\ =[2(k+1)]^{2}-4 \times(3...
For what values of 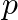 are the roots of the equation
are the roots of the equation 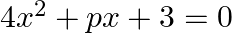 . real and equal?
. real and equal?
The given equation is $4 x^{2}+p x+3=0$. This is of the form $a x^{2}+b x+c=0$, where $a=4, b=p$ and $c=3$. $\therefore D=b^{2}-4 a c=p^{2}-4 \times 4 \times 3=p^{2}-48$ The given equation will have...
For what value of  are the roots of the quadratic equation
are the roots of the quadratic equation 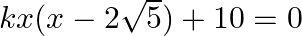 real and equal.
real and equal.
The given equation is $\begin{array}{l} k x(x-2 \sqrt{5})+10=0 \\ \Rightarrow k x^{2}-2 \sqrt{5} k x+10=0 \end{array}$ This is of the form $a x^{2}+b x+c=0$, where $a=k, b=-2 \sqrt{5} k$ and $c=10$....
If a and b are distinct real numbers, show that the quadratic equations 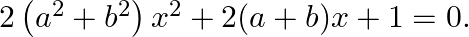 has no real roots.
has no real roots.
The given equation is $2\left(a^{2}+b^{2}\right) x^{2}+2(a+b) x+1=0$ $\begin{array}{l} \therefore D=[2(a+b)]^{2}-4 \times 2\left(a^{2}+b^{2}\right) \times 1 \\ =4\left(a^{2}+2 a...
Find the nature of roots of the following quadratic equations:
(i) 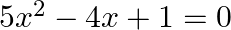
(ii) 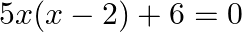
(i) The given equation is $5 x^{2}-4 x+1=0$ This is of the form $a x^{2}+b x+c=0$, where $a=5, b=-4$ and $c=1$. $\therefore$ Discriminant, $D=b^{2}-4 a c=(-4)^{2}-4 \times 5 \times 1=16-20=-4<0$...
Find the roots of the each of the following equations, if they exist, by applying the quadratic formula: 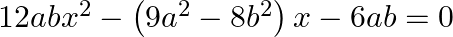 , where
, where 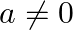 and
and 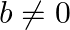
$12 a b x^{2}-\left(9 a^{2}-8 b^{2}\right) x-6 a b=0$ On comparing it with $A x^{2}+B x+C=0$, we get: $A=12 a b, B=-\left(9 a^{2}-8 b^{2}\right)$ and $C=-6 a b$ Discriminant $D$ is given by:...
Find the roots of the each of the following equations, if they exist, by applying the quadratic formula: 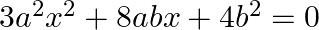
$3 a^{2} x^{2}+8 a b x+4 b^{2}=0$ On comparing it with $A x^{2}+B x+C=0$, we get: $A=3 a^{2}, B=8 a b$ and $C=4 b^{2}$ Discriminant $D$ is given by: $\begin{array}{l} D=\left(B^{2}-4 A C\right) \\...
Find the roots of the each of the following equations, if they exist, by applying the quadratic formula: 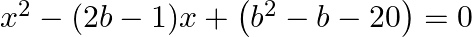 .
.
The given equation is $x^{2}-(2 b-1) x+\left(b^{2}-b-20\right)=0$ Comparing it with $A x^{2}+B x+C=0$, we get $A=1, B=-(2 b-1)$ and $C=b^{2}-b-20$ $\therefore$ Discriminant, $D=B^{2}-4 A C=[-(2...
On a horizonal plane there is a vertical tower with a flagpole on the top of the tower. At a point, 9 meters away from the foot of the tower, the angle of elevation of the top and bottom of the flagpole are 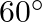 and
and 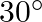 respectively. Find the height of the tower and the flagpole mounted on it
respectively. Find the height of the tower and the flagpole mounted on it
In the adjoining figure, ABC is a triangle. DE is parallel to BC and AD/DB = 3/2,
(i) Determine the ratios AD/AB, DE/BC0
(ii) Prove that ∆DEF is similar to ∆CBF. Hence, find EF/FB.
(iii) What is the ratio of the areas of ∆DEF and ∆CBF?
Solution:- (i) We have to find the ratios AD/AB, DE/BC, From the question it is given that, AD/DB = 3/2 Then, DB/AD = 2/3 Now add 1 for both LHS and RHS we get, (DB/AD) + 1 = (2/3) + 1 (DB + AD)/AD...
In the given figure, CM and RN are respectively the medians of ∆ABC and ∆PQR. If ∆ABC ~ ∆PQR, prove that:
(i) ∆AMC ~ ∆PQR
(ii) CM/RN = AB/PQ
(iii) ∆CMB ~ ∆RNQ
Solution:- From the given figure it is given that, CM and RN are respectively the medians of ∆ABC and ∆PQR. (i) We have to prove that, ∆AMC ~ ∆PQR Consider the ∆ABC and ∆PQR As ∆ABC ~ ∆PQR ∠A = ∠P,...
State which pairs of triangles in the figure given below are similar. Write the similarity rule used and also write the pairs of similar triangles in symbolic form (all lengths of sides are in cm):
Solution:- (i) From the ΔABC and ΔPQR AB/PQ = 3.2/4 = 32/40 Divide both numerator and denominator by 8 we get, = 4/5 AC/PR = 3.6/4.5 = 36/45 Divide both numerator and denominator by 9 we get, = 4/5...
Two different dice are thrown at the same time. Find the probability of getting :
(iii) sum divisible by 5
(iv) sum of at least 11.
(iii)Let E be an event of getting a sum divisible by 5. Favourable outcomes = {(1,4),(2,3), (3,2), (4,1),(4,6), (5,5), (6,4)} Number of favourable outcomes = 7 P(E) = 7/36 Probability of getting a...
Two different dice are thrown at the same time. Find the probability of getting :
(i) a doublet
(ii) a sum of 8
Solution: When two dice are thrown simultaneously, the sample space of the experiment is {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,1), (2,2), (2,3), (2,4), (2,5), (2,6), (3,1),(3,2), (3,3),...
Two different dice are thrown simultaneously. Find the probability of getting:
(i) a number greater than 3 on each dice
(ii) an odd number on both dice.
Solution: When two dice are thrown simultaneously, the sample space of the experiment is {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,1), (2,2), (2,3), (2,4), (2,5), (2,6), (3,1),(3,2), (3,3),...
From a pack of 52 cards, a blackjack, a red queen and two black kings fell down. A card was then drawn from the remaining pack at random. Find the probability that the card drawn is
(i) a black card
(ii) a king
(iii) a red queen.
Solution: Total number of cards = 52-4 = 48 [∵4 cards fell down] So number of possible outcomes = 48 (i) Let E be the event of getting black card. There will be 23 black cards since a black jack and...
All the three face cards of spades are removed from a well-shuffled pack of 52 cards. A card is then drawn at random from the remaining pack. Find the probability of getting
(v) a spade
(vi) ‘9’ of black colour.
(v) Let E be the event of getting a spade. There will be 10 spades. Number of favourable outcomes = 10 P(E) = 10/49 Hence the probability of getting a spade is 10/49. (vi) Let E be the event of...
A card is drawn from a well-shuffled pack of 52 cards. Find the probability of getting:
(iii) a king of red colour
(iv) a card of diamond
(iii) Let E be the event of getting a king of red colour. There will be 2 cards of king of red colour. Number of favourable outcomes = 2 P(E) = 2/52 = 1/26 Hence the probability of getting a king of...
A card is drawn from a well-shuffled pack of 52 cards. Find the probability of getting:
(i) ‘2’ of spades
(ii) a jack .
Solution: Total number of cards = 52. So number of possible outcomes = 52. (i) Let E be the event of getting ‘2’ of spades. There will be only one card of ‘2’ spades. Number of favourable outcomes =...
A box contains 15 cards numbered 1, 2, 3,…..15 which are mixed thoroughly. A card is drawn from the box at random. Find the probability that the number on the card is :
(v) divisible by 3 or 2
(vi) a perfect square number.
(v) Let E be the event of getting the number on the card is divisible by 3 or 2 Outcomes favourable to E are {2,3,4,6,8,9,10,12,14,15} Number of favourable outcomes = 10 P(E) = 10/15 = 2/3 Hence the...
Find the probability that the month of February may have 5 Wednesdays in
(i) a leap year
(ii) a non-leap year.
Solution: There are 7 ways in which the month of February can occur, each starting with a different day of the week. (i)Only 1 way is possible for 5 Wednesdays to occur in February with 29 days....
Find the probability that the month of January may have 5 Mondays in
(i) a leap year
(ii) a non-leap year.
Solution: For a leap year there are 366 days. Number of days in January = 31 Total number of January month types = 7 Number of January months with 5 Mondays = 3 (i)Probability that the month of...
A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (shown in the adjoining figure) and these are equally likely outcomes. What is the probability that it will point at
(iii) a number greater than 2?
(iv) a number less than 9?
(iii) Let E be the event of arrow pointing a number greater than 2. Outcomes favourable to E are {3,4,5,6,7,8} Number of favourable outcomes = 6 P(E) = 6/8 = 3/4 Hence the probability of arrow...
In a single throw of a die, find the probability of getting:
(iii) a number greater than 5
(iv) a prime number
(iii)Let E be the event of getting a number greater than 5. Outcomes favourable to E is 6. Number of favourable outcomes = 1 P(E) = 1/6 Hence the probability of getting a number greater than 5 is...
In a single throw of a die, find the probability of getting:
(i) an odd number
(ii) a number less than 5
Solution: When a die is thrown, the possible outcomes are 1,2,3,4,5,6. Number of possible outcomes = 6 (i) Let E be the event of getting an odd number. Outcomes favourable to E are 1,3,5. Number of...
A box contains 7 blue, 8 white and 5 black marbles. If a marble is drawn at random from the box, what is the probability that it will be
(i) black?
(ii) blue or black?
Solution: Number of blue marbles = 7 Number of white marbles = 8 Number of black marbles = 5 Total number of marbles = 7+8+5 = 20 (i) Probability of getting black , = 5/20 = 1/4 Hence the...
A bag contains 5 black, 7 red and 3 white balls. A ball is drawn at random from the bag, find the probability that the ball drawn is: (i) red (ii) black or white (iii) not black.
Solution: Number of black balls = 5 Number of red balls = 7 Number of white balls = 3 Total number of balls = 5+7+3 = 15 (i)Probability that the ball drawn is red, = 7/15 (ii) Probability of black...
A letter of English alphabet is chosen at random. Determine the probability that the letter is a consonant.
Solution: Total number of alphabets = 26 Number of vowels = 5 Total number of consonants = 26-5 = 21 Probability that the letter chosen is a consonant , = 21/26 Hence the required probability is...
