Answer: 1 ×10 1 = remainder obtained by dividing 1 × 1 by 10 = 1 3 ×10 7 = remainder obtained by dividing 3 × 7 by 10 = 1 7 ×10 9 = remainder obtained by dividing 7 × 9 by 10 = 3 Composition table:...
Construct the composition table for ×5 on set Z5 = {0, 1, 2, 3, 4}
Answer: 1 ×5 1 = remainder obtained by dividing 1 × 1 by 5 = 1 3 ×5 4 = remainder obtained by dividing 3 × 4 by 5 = 2 4 ×5 4 = remainder obtained by dividing 4 × 4 by 5 = 1 Composition table: ×5 0 1...
Construct the composition table for ×6 on set S = {0, 1, 2, 3, 4, 5}.
Answer: 1 ×6 1 = remainder obtained by dividing 1 × 1 by 6 = 1 3 ×6 4 = remainder obtained by dividing 3 × 4 by 6 = 0 4 ×6 5 = remainder obtained by dividing 4 × 5 by 6 = 2 Composition table: ×6 0 1...
Construct the composition table for +5 on set S = {0, 1, 2, 3, 4}
Answer: 1 +5 1 = remainder obtained by dividing 1 + 1 by 5 = 2 3 +5 1 = remainder obtained by dividing 3 + 1 by 5 = 2 4 +5 1 = remainder obtained by dividing 4 + 1 by 5 = 3 Composition Table: +5 0 1...
Construct the composition table for ×4 on set S = {0, 1, 2, 3}.
Answer: Given, ×4 on set S = {0, 1, 2, 3} 1 ×4 1 = remainder obtained by dividing 1 × 1 by 4 = 1 0 ×4 1 = remainder obtained by dividing 0 × 1 by 4 = 0 2 ×4 3 = remainder obtained by dividing 2 × 3...
Let * be a binary operation on Z defined by a * b = a + b – 4 for all a, b ∈ Z. (i) Show that * is both commutative and associative. (ii) Find the identity element in Z
Answers: (i) Consider, a, b ∈ Z a * b = a + b – 4 = b + a – 4 = b * a a * b = b * a, ∀ a, b ∈ Z Then, * is commutative on Z. a * (b * c) = a * (b + c – 4) = a + b + c -4 – 4 = a + b + c – 8 (a * b)...
Let * be a binary operation on Q0 (set of non-zero rational numbers) defined by a * b = (3ab/5) for all a, b ∈ Q0. Show that * is commutative as well as associative. Also, find its identity element, if it exists.
Answer: Consider, a, b ∈ Q0 a * b = (3ab/5) = (3ba/5) = b * a a * b = b * a, for all a, b ∈ Q0 a * (b * c) = a * (3bc/5) = [a (3 bc/5)] /5 = 3 abc/25 (a * b) * c = (3 ab/5) * c = [(3 ab/5)...
Let * be a binary operation on Q – {-1} defined by a * b = a + b + ab for all a, b ∈ Q – {-1}. Then, (i) Show that * is both commutative and associative on Q – {-1} (ii) Find the identity element in Q – {-1}
Answers: (i) Consider, a, b ∈ Q – {-1} a * b = a + b + ab = b + a + ba = b * a a * b = b * a, ∀ a, b ∈ Q – {-1} a * (b * c) = a * (b + c + b c) = a + (b + c + b c) + a (b + c + b c) = a + b +...
Let * be a binary operation on Q – {-1} defined by a * b = a + b + ab for all a, b ∈ Q – {-1}. Then, Show that every element of Q – {-1} is invertible. Also, find inverse of an arbitrary element.
Answer: Consider, a ∈ Q – {-1} and b ∈ Q – {-1} be the inverse of a. a * b = e = b * a a * b = e and b * a = e a + b + ab = 0 and b + a + ba = 0 b (1 + a) = – a Q – {-1} b = -a/1 + a Q – {-1}...
Let A = R0 × R, where R0 denote the set of all non-zero real numbers. A binary operation ‘O’ is defined on A as follows: (a, b) O (c, d) = (ac, bc + d) for all (a, b), (c, d) ∈ R0 × R. (i) Show that ‘O’ is commutative and associative on A (ii) Find the identity element in A
Answers: (i) Consider, X = (a, b) Y = (c, d) ∈ A, ∀ a, c ∈ R0 b, d ∈ R X O Y = (ac, bc + d) Y O X = (ca, da + b) X O Y = Y O X, ∀ X, Y ∈ A O is not commutative on A. X = (a, b) Y = (c, d) a Z = (e,...
Let A = R0 × R, where R0 denote the set of all non-zero real numbers. A binary operation ‘O’ is defined on A as follows: (a, b) O (c, d) = (ac, bc + d) for all (a, b), (c, d) ∈ R0 × R. Find the invertible element in A.
Answer: Consider, F = (m, n) be the inverse in A ∀ m ∈ R0 and n ∈ R X O F = E F O X = E (am, bm + n) = (1, 0) and (ma, na + b) = (1, 0) Considering (am, bm + n) = (1, 0) am = 1 m = 1/a And bm + n =...
Let * be a binary operation on Z defined by a * b = a + b – 4 for all a, b ∈ Z. Find the invertible element in Z.
Answer: Consider, a ∈ Z and b ∈ Z be the inverse of a. a * b = e = b * a a * b = e and b * a = e a + b – 4 = 4 and b + a – 4 = 4 b = 8 – a ∈ Z Hence, 8 – a is the inverse of a ∈...
Find the identity element in the set of all rational numbers except – 1 with respect to * defined by a * b = a + b + ab
Answer: Consider, e be the identity element in I+ with respect to * such that a * e = a = e * a, ∀ a ∈ Q – {-1} a * e = a and e * a = a, ∀ a ∈ Q – {-1} a + e + ae = a and e + a + ea = a, ∀ a ∈ Q –...
Find the identity element in the set I+ of all positive integers defined by a * b = a + b for all a, b ∈ I+.
Answer: Consider, e be the identity element in I+ with respect to * a * e = a = e * a, ∀ a ∈ I+ a * e = a and e * a = a, ∀ a ∈ I+ a + e = a and e + a = a, ∀ a ∈ I+ e = 0, ∀ a ∈ I+ Hence, 0 is the...
Differentiate 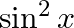 with respect to
with respect to 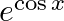
As per the given question,
Differentiate 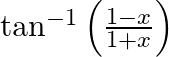 with respect to
with respect to 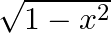 , if
, if 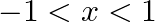
As per the given question,
Differentiate 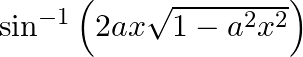 with respect to
with respect to 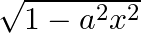 , if
, if 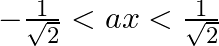
As per the given question,
Differentiate 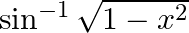 with respect to
with respect to 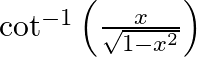 , if
, if 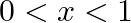
As per the given question,
Differentiate 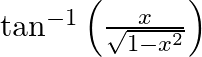 with respect to
with respect to 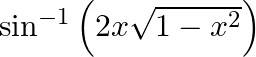 , if
, if 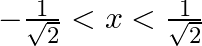
As per the given question,
Differentiate 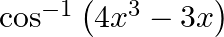 with respect to
with respect to 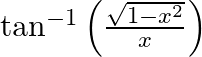 , if
, if 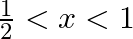
As per the given question,
Differentiate 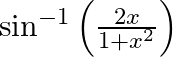 with respect to
with respect to 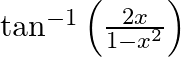 , if
, if 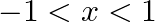
As per the given question,
Differentiate 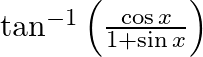 with respect to
with respect to 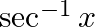
As per the given question,
Differentiate  with respect to
with respect to 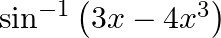 , if
, if 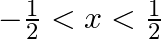
As per the given question,
Differentiate 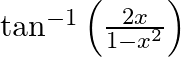 with respect to
with respect to 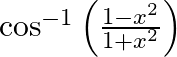 , if
, if 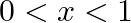
As per the given question,
Differentiate 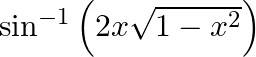 with respect to
with respect to 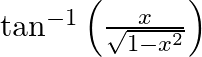 , if
, if 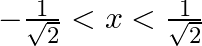
As per the given question,
Differentiate 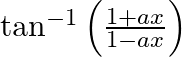 with respect to
with respect to 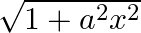
As per the given question,
Differentiate 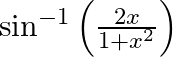 with respect to
with respect to 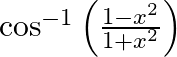 , if
, if 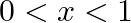
As per the given question,
Differentiate 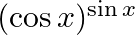 with respect to
with respect to 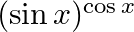 .
.
As per the given question, ......(i) ........(ii)
Differentiate 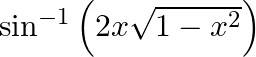 with respect to
with respect to 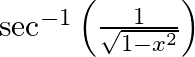 , if
, if 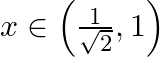
As per the given question,
Differentiate 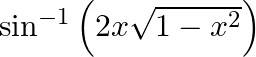 with respect to
with respect to 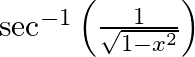 , if
, if 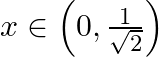
As per the given question,
Differentiate 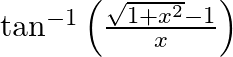 with respect to
with respect to 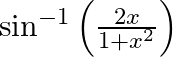 , if
, if 
As per the given question,
Differentiate 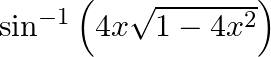 with respect to
with respect to 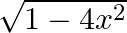 , if
, if 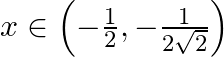
As per the given question,
Differentiate 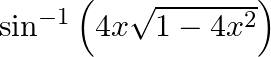 with respect to
with respect to 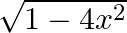 , if
, if 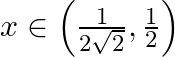
As per the given question,
Differentiate 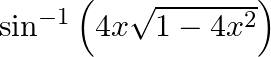 with respect to
with respect to 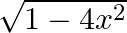 , if
, if 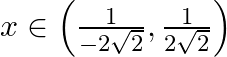
As per the given question,
Differentiate 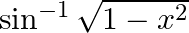 with respect to
with respect to 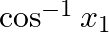 if
if 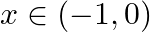
As per the given question,
Differentiate 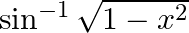 with respect to
with respect to 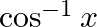 , if
, if 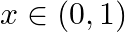
As per the given question,
Differentiate 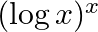 with respect to
with respect to 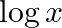
As per the given question,
Differentiate 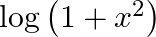 with respect to
with respect to 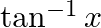
As per the given question,
Differentiate 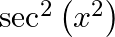 with respect to
with respect to 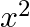
As per the given question,
If 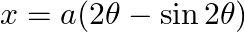 and
and 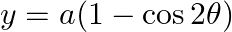 , find
, find 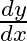 when
when 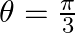
As per the given question,
If 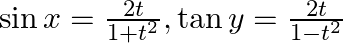 find
find 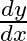
As per the given question,
If 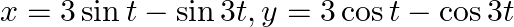 , find
, find 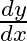 at
at 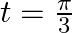 .
.
As per the given question,
If 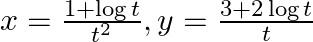 , find
, find 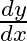
As per the given question,
If 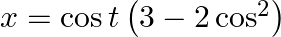 and
and 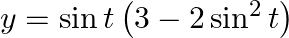 find the value of
find the value of 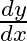 at
at 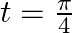
As per the given question,
If 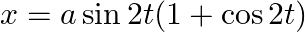 and
and 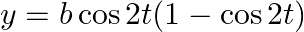 , show that at
, show that at 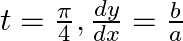 .
.
As per the given question,
If 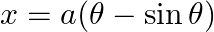 and
and 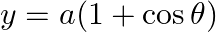 find
find 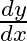 , at
, at 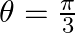 .
.
As per the given question,
Find 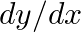 , if
, if 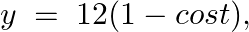
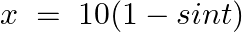
As per the given question,
If 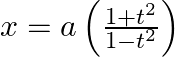 and
and 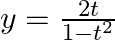 , find
, find 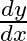
As per the given question,
If 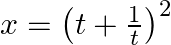 and
and 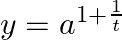 , find
, find 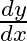
As per the given question,
If  and
and  are connected parametrically by the equation, without eliminating the parameter, find
are connected parametrically by the equation, without eliminating the parameter, find 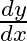 .
. 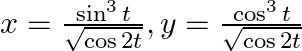
As per the given question,
If 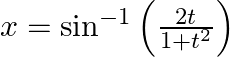 and
and 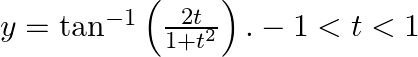 , prove that
, prove that 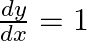
As per the given question,
If 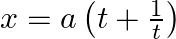 and
and 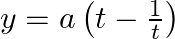 , prove that
, prove that 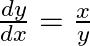 .
.
As per the given question,
If 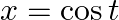 and
and 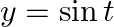 , prove that
, prove that 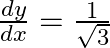 at
at 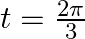
As per the given question,
If 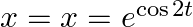 and
and 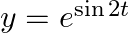 , prove that
, prove that 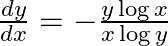
As per the given question,
If 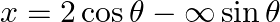 and
and 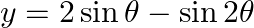 , prove that
, prove that 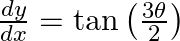
As per the given question,
Find 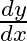 , when
, when 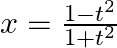 and
and 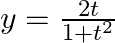
As per the given question,
Find 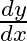 , when
, when 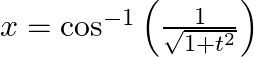 and
and 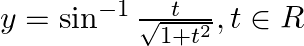
As per the given question,
Find 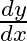 , when
, when 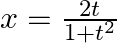 and
and 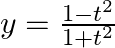
As per the given question,
Find 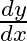 , when Find
, when Find 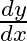 , when
, when 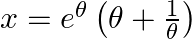 and
and 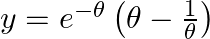
As per the given question,
If  and
and  are connected parametrically by the equation, without eliminating the parameter, find
are connected parametrically by the equation, without eliminating the parameter, find 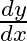 .
. 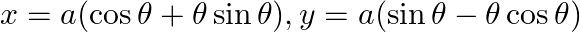
As per the given question,
Find 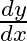 , when
, when 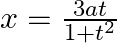 and
and 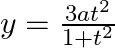
As per the given question,
Find 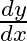 , when
, when 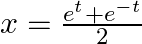 and
and 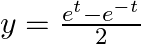
As per the given question,
Find 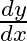 , when
, when 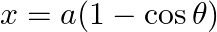 and
and 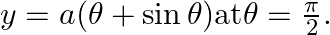
As per the given question,
Find 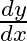 , when
, when 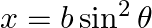 and
and 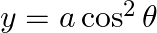
As per the given question,
Find 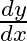 , when
, when 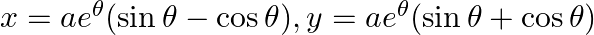
As per the given question,
Find 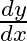 , when
, when 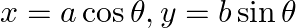
As per the given question,
Find 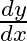 , when
, when 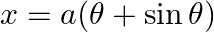 and
and 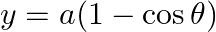
As per the given question,
Find 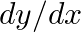 when:
when: 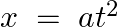 and
and 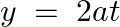
We have, $y=2 a t$ $\frac{d y}{d t}=2 a \frac{d}{d t}(t)=2 a(1)=2 a \\ \text { also } x=a t^{2} \\ \frac{d x}{d x}=a \frac{d}{d t}\left(t^{2}\right)=a(2 t)=2 a t \\ \text { now } \frac{d y}{d...
A laboratory blood test is 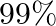 effective in detecting a certain disease when it is in fact, present. However, the test also yields a false positive result for
effective in detecting a certain disease when it is in fact, present. However, the test also yields a false positive result for 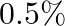 of the healthy person tested (that is, if a healthy person is tested, then, with probability
of the healthy person tested (that is, if a healthy person is tested, then, with probability 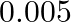 , the test will imply he has the disease). If
, the test will imply he has the disease). If 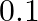 percent of the population actually has the disease, what is the probability that a person has the disease given that his test result is positive?
percent of the population actually has the disease, what is the probability that a person has the disease given that his test result is positive?
As per the given question,
In answering a question on a multiple choice test a student either knows the answer or guesses. Let 3/4 be the probability that he knows the answer and 1/4 be the probability that he guesses. Assuming that a student who guesses at the answer will be correct with probability 1/4. What is the probability that a student knows the answer given that he answered it correctly?
As per the given question,
A speaks the truth 8 times out of 10 times. A die is tossed. He reports that it was 5 What is the probability that it was actually 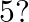
As per the given question,
 is known to speak truth 3 times out of 5 times. He throws a die and reports that it is
is known to speak truth 3 times out of 5 times. He throws a die and reports that it is 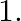 Find the probability that it is actually
Find the probability that it is actually 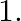
As per the given question,
Let 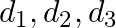 be three mutually exclusive diseases. Let
be three mutually exclusive diseases. Let 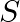 be the set of observable symptoms of these diseases. A doctor has the following information from a random sample of 5000 patients: 1800 had disease
be the set of observable symptoms of these diseases. A doctor has the following information from a random sample of 5000 patients: 1800 had disease 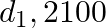 has disease
has disease 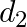 and the others had disease
and the others had disease 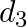 1500 patients with disease
1500 patients with disease  patients with disease
patients with disease 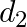 and 900 patients with disease
and 900 patients with disease 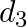 showed the symptom. Which of the diseases is the patient most likely to have?
showed the symptom. Which of the diseases is the patient most likely to have?
As per the given question,
A test for detection of a particular disease is not fool proof. The test will correctly detect the disease 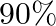 of the time, but will incorrectly detect the disease
of the time, but will incorrectly detect the disease 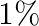 of the time. For a large population of which an estimated
of the time. For a large population of which an estimated 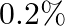 have the disease, a person is selected at random, given the test, and told that he has the disease. What are the chances that the person actually have the disease?
have the disease, a person is selected at random, given the test, and told that he has the disease. What are the chances that the person actually have the disease?
As per the given question,
By examining the chest 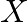 -ray, probability that T.B is detected when a person is actually suffering is
-ray, probability that T.B is detected when a person is actually suffering is  . The probability that the doctor diagnoses incorrectly that a person has T.B. on the basis of
. The probability that the doctor diagnoses incorrectly that a person has T.B. on the basis of 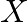 -ray is
-ray is 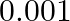 . In a certain city 1 in 100 persons suffers from T.B. A person is selected at random is diagnosed to have T.B. What is the chance that he actually has T.B.?
. In a certain city 1 in 100 persons suffers from T.B. A person is selected at random is diagnosed to have T.B. What is the chance that he actually has T.B.?
As per the given question,
If a machine is correctly set up, it produces 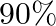 acceptable items. If it is incorrectly set up, it produces only
acceptable items. If it is incorrectly set up, it produces only 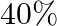 acceptable item s. Past experience shows that
acceptable item s. Past experience shows that 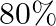 of the set ups are correctly done. If after a certain set up, the machine produces 2 acceptable items, find the probability that the machine is correctly setup.
of the set ups are correctly done. If after a certain set up, the machine produces 2 acceptable items, find the probability that the machine is correctly setup.
As per the given question,
Coloured balls are distributed in four boxes as shown in the following table ![Rendered by QuickLaTeX.com \[\begin{tabular}{cc|c|c|c} \hline Box & \multicolumn{3}{c}{ Colour } \\ & Black & White & Red & Blue \\ \hline I & 3 & 4 & 5 & 6 \\ \hline II & 2 & 2 & 2 \\ \hline III & 1 & 2 & 1 \\ \hline IV & 4 & 3 & 5 \\ \hline \end{tabular}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-22c35adcd58fd61079fed1526e84cfa7_l3.png)
A box is selected at random and then a ball is randomly drawn from the selected box. The colour of the ball is black, what is the probability that ball drawn is from the box III.
![Rendered by QuickLaTeX.com \[\begin{tabular}{cc|c|c|c} \hline Box & \multicolumn{3}{c}{ Colour } \\ & Black & White & Red & Blue \\ \hline I & 3 & 4 & 5 & 6 \\ \hline II & 2 & 2 & 2 \\ \hline III & 1 & 2 & 1 \\ \hline IV & 4 & 3 & 5 \\ \hline \end{tabular}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-22c35adcd58fd61079fed1526e84cfa7_l3.png)
As per the given question,
Assume that the chances of the patient having a heart attack are 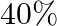 . It is also assumed that a meditation and yoga course reduce the risk of heart attack by
. It is also assumed that a meditation and yoga course reduce the risk of heart attack by 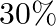 and prescription of certain drug reduces its chances by
and prescription of certain drug reduces its chances by 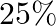 . At a time a patient can choose any one of the two options with equal probabilities. It is given that after going through one of the two options the patient selected at random suffers a heart attack. Find the probability that the patient followed a course of meditation and yoga?
. At a time a patient can choose any one of the two options with equal probabilities. It is given that after going through one of the two options the patient selected at random suffers a heart attack. Find the probability that the patient followed a course of meditation and yoga?
As per the given question,
There are three coins. One is two headed coin (having head on both faces), another is a biased coin that comes up heads 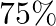 of the time and third is an unbiased coin. One of the three coins is chosen at random and tossed, it shows heads, what is the probability that it was the two headed coin?
of the time and third is an unbiased coin. One of the three coins is chosen at random and tossed, it shows heads, what is the probability that it was the two headed coin?
As per the given question,
Of the students in a college, it is known that 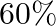 reside in a hostel and
reside in a hostel and 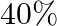 do not reside in hostel. Previous year results report that
do not reside in hostel. Previous year results report that 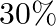 of students residing in hostel attain
of students residing in hostel attain  grade and
grade and 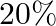 of ones not residing in hostel attain
of ones not residing in hostel attain  grade in their annual examination. At the end of the year, one students is chosen at random from the college and he has an A grade. What is the probability that the selected student is a hosteller?
grade in their annual examination. At the end of the year, one students is chosen at random from the college and he has an A grade. What is the probability that the selected student is a hosteller?
As per the given question,
An insurance company insured 2000 scooters and 300 motorcycles. The probability of an accident involving a scooter is 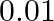 and that of a motorcycle is
and that of a motorcycle is 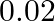 . An insured vehicle met whith an accident. Find the probability that the accident vehicle was a motorcycle
. An insured vehicle met whith an accident. Find the probability that the accident vehicle was a motorcycle
As per the given question,
For 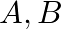 and
and  the chances of being selected as the manager of a firm are in the ratio
the chances of being selected as the manager of a firm are in the ratio 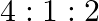 respectively. The respective probabilities for them to introduce a radical change in marketing startegy are
respectively. The respective probabilities for them to introduce a radical change in marketing startegy are  and
and 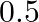 . If the change does take place, find the probability that it is due to the appointment of
. If the change does take place, find the probability that it is due to the appointment of  or
or  .
.
As per the given question,
In a certain college,  of boys and
of boys and 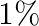 of girls are taller than
of girls are taller than 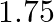 meters. Further more,
meters. Further more, 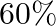 of the students in the college are girls. A student selected at random from the college is found to be taller than
of the students in the college are girls. A student selected at random from the college is found to be taller than 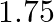 meters. Find the probability that the selected student is girl.
meters. Find the probability that the selected student is girl.
As per the given question,
A bag contains 1 white and 6 red balls, and a second bag contains 4 white and 3 red balls. One of the bags is picked up at random and a ball is randomly drawn from it, and is found to be white in colour. Find the probability that the drawn ball was from the first bag.
As per the given question,
A factory has three machines 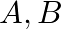 and
and  , which produce 100,200 and 300 items of a particular type daily. The machines produœe
, which produce 100,200 and 300 items of a particular type daily. The machines produœe 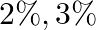 and
and 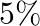 defective items respectively. One day when the production was over, an item was picked up randomly and it was found to be defective. Find the probability that it was produced by machine
defective items respectively. One day when the production was over, an item was picked up randomly and it was found to be defective. Find the probability that it was produced by machine  .
.
As per the given question,
In a group of 400 people, 160 are smokers and non-vegetarian, 100 are smokers and vegetarian and the remaining are nonsmokers and veqetarian. The probabilities of aettina a special chest disease are 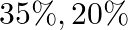 and
and 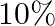 respectively. A person is chosen from the group at random and is found to be suffering from the disease. What is the probability that the selected person is a smoker and non-vegetarian?
respectively. A person is chosen from the group at random and is found to be suffering from the disease. What is the probability that the selected person is a smoker and non-vegetarian?
As per the given question,
Three urns 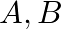 and
and  contain 6 red and 4 white; 2 red and 6 white; and 1 red and 5 white balls redpectively. an urn is chosen at random and a ball is drawn. If the ball drawn is found to be red, find the probability that the ball was drawn from urn
contain 6 red and 4 white; 2 red and 6 white; and 1 red and 5 white balls redpectively. an urn is chosen at random and a ball is drawn. If the ball drawn is found to be red, find the probability that the ball was drawn from urn  .
.
As per the given question,
A company has two plants to manufacture bicycles. The first plant manufactures 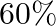 of the bicycles and the second plant
of the bicycles and the second plant 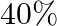 . Out of that
. Out of that 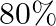 of the bicycles are rated of standard quality at the first plant and
of the bicycles are rated of standard quality at the first plant and 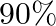 of standard quality at the second plant. A bicycle is picked up at random and found to be standard quality. Find the probability that it comes from the second plant.
of standard quality at the second plant. A bicycle is picked up at random and found to be standard quality. Find the probability that it comes from the second plant.
As per the given question,
In a factory, machine  produces
produces 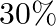 of the total output, machine
of the total output, machine  produces
produces 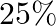 and the machine
and the machine  produces the remaining output. If defective items produced by machines
produces the remaining output. If defective items produced by machines 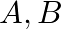 and
and  are
are 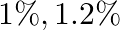 respectively. Three machines working output and found to be defective. Find the probability that it was produced by machine
respectively. Three machines working output and found to be defective. Find the probability that it was produced by machine  ?
?
As per the given question,
There are three coins. One is two-headed coin (having head on both faces), another is biased coin that comes up heads 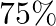 of the times and third is also a biased coin that comes up tail
of the times and third is also a biased coin that comes up tail 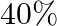 of the times. One of the three coins is chosen at random and tossed, and it shows heads. What is the probability that it was the two-headed coin?
of the times. One of the three coins is chosen at random and tossed, and it shows heads. What is the probability that it was the two-headed coin?
As per the given question,
An item is manufactured by three machine A, B and C. out of the total number of items manufactured durina a specified period. 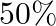 are manufacture on machine A
are manufacture on machine A 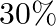 on
on  and
and 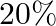 on C.
on C. 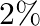 of the items produced on
of the items produced on 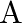 and
and 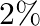 of items produced on
of items produced on 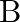 are defective and
are defective and 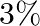 of these produced on
of these produced on 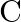 are defective. All the items stored at one godown. One items is drawn at random and is found to be defective. What is the probability that it was manufactured on machine A?
are defective. All the items stored at one godown. One items is drawn at random and is found to be defective. What is the probability that it was manufactured on machine A?
As per the given question,
A manufacturer has three machine operators 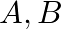 and
and  . The first operator A produces
. The first operator A produces 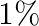 defective items, where as the other two operators
defective items, where as the other two operators  and
and  produce
produce 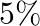 and
and 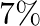 defective items respectively.
defective items respectively.  is on the job for
is on the job for 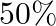 of the time,
of the time,  is on the job for
is on the job for 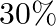 of the time and
of the time and 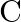 is on the job for
is on the job for 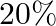 of the time. A defective item is produced, what is the probability that was produced by
of the time. A defective item is produced, what is the probability that was produced by  ?
?
As per the given question,
Suppose we have four boxes 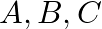 and
and 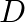 containing coloured marbles as given below:
containing coloured marbles as given below: ![Rendered by QuickLaTeX.com \[\begin{tabular}{|c|c|c|c|} \hline Box & \multicolumn{3}{|c|}{ Colour } \\ \cline { 2 - 4 } & Red & White & Black \\ \hline A & 1 & 6 & 3 \\ \hline B & 6 & 2 & 2 \\ \hline C & 8 & 1 & 1 \\ \hline D & 0 & 6 & 4 \\ \hline \end{tabular}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7e969fd3ae37333f22397872de21f8c2_l3.png)
one of the boxes has been selected at random and a single marble is drawn from it. If the marble is red, what is the probability that it was drawn from that box  ? Box B? Box C?
? Box B? Box C?
![Rendered by QuickLaTeX.com \[\begin{tabular}{|c|c|c|c|} \hline Box & \multicolumn{3}{|c|}{ Colour } \\ \cline { 2 - 4 } & Red & White & Black \\ \hline A & 1 & 6 & 3 \\ \hline B & 6 & 2 & 2 \\ \hline C & 8 & 1 & 1 \\ \hline D & 0 & 6 & 4 \\ \hline \end{tabular}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7e969fd3ae37333f22397872de21f8c2_l3.png)
As per the given question,
An insurance company issued 3000 scooters, 4000 cars and 5000 trucks. The probabilities of the accident involving a scooter, a car and a truck are 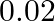 ,
, 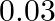 and
and  respectively. One of the insured vehicles meet with an accident Find the probability that it is a truck.
respectively. One of the insured vehicles meet with an accident Find the probability that it is a truck.
As per the given question,
An insurance company issued 3000 scooters, 4000 cars and 5000 trucks. The probabilities of the accident involving a scooter, a car and a truck are 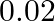 ,
, 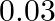 and
and  respectively. One of the insured vehicles meet with an accident Find the probability that it is a (i) scooter (ii) car
respectively. One of the insured vehicles meet with an accident Find the probability that it is a (i) scooter (ii) car
As per the given question,
A factory has three machines X, Y, and Z producing 1000, 2000 and 3000 bolts per day respectively. The machine X produces 1% defective bolts, Y produces 1.5% and Z produces 2% defective bolts. At the end of the day, a bolt is drawn at random and is found to be defective. What is the probability that this defective bolt has been produced by machine?
Total number of bolts produced in day =(1000+2000+3000) =6000 Let E1, E2 and E3 be the events of drawing a bolt produced by machines X, Y and Z respectively. Then, P(E)=1000/6000=1/6,...
In a class, 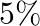 of the boys and
of the boys and 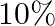 of the girls have an IQ of more than
of the girls have an IQ of more than 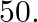 In this class,
In this class, 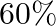 of the students are boys. If a student is selected at random and found to have an IQ of more than 150 , find the probability that the student is a boy.
of the students are boys. If a student is selected at random and found to have an IQ of more than 150 , find the probability that the student is a boy.
As per the given question,
A letter is known to have come either from LONDON or CLIFTON. On the envelope just two consecutive letters 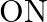 are visible. What is the probability that the letter has come from (i) LONDON (ii) CLIFTON?
are visible. What is the probability that the letter has come from (i) LONDON (ii) CLIFTON?
As per the given question,
Suppose 5 men out of 100 and 25 women out of 1000 are good orators. An orator is chosen at random. Find the probability that a male person is selected. Assume that there are equal number of men and women.
As per the given question,
Two groups are competing for the positions of the Board of Directors of a Corporation. The probabilities that the first and the second groups will win are 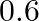 and
and 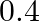 respectively. Further, if the first group wins, the probability of introducing a new product is
respectively. Further, if the first group wins, the probability of introducing a new product is 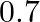 and the correspond ing probability is
and the correspond ing probability is 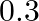 if the second group wins. Find the probability that the new product introduced was by the second group.
if the second group wins. Find the probability that the new product introduced was by the second group.
As per the given question,
Suppose a girl throws a die. If she gets 1 or 2 , she tosses a coin three times and notes the number of tails. If she gets  or 6 , she tosses a coin once and notes whether a ‘head’ or ‘tail’ is obtained. If she obtained exactly one ‘tail’, what is the probability that she threw
or 6 , she tosses a coin once and notes whether a ‘head’ or ‘tail’ is obtained. If she obtained exactly one ‘tail’, what is the probability that she threw  or 6 with the die?
or 6 with the die?
As per the given question,
The contents of three urns are as follows: Urn 1: 7 white, 3 black balls, Urn 2: 4 white, 6 black balls, and Urn 3: 2 white, 8 black balls. One of these urns is chosen at random with probabilities 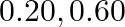 and
and 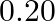 respectively. From the chosen urn two balls are drawn at random without replacement. If both these balls are white, what is the probability that these came from urn 3 ?
respectively. From the chosen urn two balls are drawn at random without replacement. If both these balls are white, what is the probability that these came from urn 3 ?
As per the given question,
Three urns contain 2 white and 3 black balls; 3 white and 2 black balls and 4 white and 1 black ball respectively. One ball is drawn from an urn chosen at random and it was found to be white. Find the probability that it was drawn from the first urn.
As per the given question,
A bag  contains 2 white and 3 red balls and a bag
contains 2 white and 3 red balls and a bag  contains 4 white and 5 red balls. One ball is drawn at random from one of the bags and is found to be red. Find the probability that it was drawn from bag
contains 4 white and 5 red balls. One ball is drawn at random from one of the bags and is found to be red. Find the probability that it was drawn from bag  .
.
As per the given question,
The contents of urns, I, II, III are as follows: Urn I: 1 white, 2 black and 3 red balls Urn II: 2 white, 1 black and 1 red balls Urn III: 4 white, 5 black and 3 red balls. One urn is chosen at random and two balls are drawn. They happen to be white and red. What is the probability that they come from Urns, I, II, III?
As per the given question,
Three machines E 1,E 2,E 3 in a certain factory produce 50%, 25% and 25% respectively, of the total daily output of electric bulbs. It is known that 4% of the tubes produced one each of machines E 1 and E 2 are defective, and that 5% of those produced on E 3 are defective. If one tube is picked up at random from a day’s production, calculate the probability that it is defective.
Let A1: Event that the bulb is produced by machine E1 A2: Event that the bulb is produced by machine E2 A3: Event that the bulb is produced by machine E3 A: Event that the picked up bulb is...
A bag contains 6 red and 8 black balls and another bag contains 8 red and 6 black balls. A ball is drawn from the first bag and without noticing its colour is put in the second bag. A ball is drawn from the second bag. Find the probability that the ball drawn is red in colur.
As per the given question,
An urn contains 10 white and 3 black balls. Another urn contains 3 white and 5 black balls. Two are drawn from first urn and put into the second urn and then a ball is drawn from the latter. Find the probability that it is a white ball.
As per the given question,
One bag contains 4 white and 5 black balls. Another bag contains 6 white and 7 black balls. A ball is transferred from first bag to the second bag and then a ball is drawn from the second bag. Find the probability that the ball drawn is white.
As per the given question,
A bag contains 4 white and 5 black balls and another bag contains 3 white and 4 black balls. A ball is taken out from the first bag and without seeing its colour is put in the second bag. A ball is taken out from the later. Find the probability that the ball drawn is white.
As per the given question,
The bag  contains 8 white and 7 black balls while the bag
contains 8 white and 7 black balls while the bag  contains 5 white and 4 black balls. One ball is randomly picked up from the bag
contains 5 white and 4 black balls. One ball is randomly picked up from the bag  and mixed up with the balls in baq
and mixed up with the balls in baq  . Then a ball is randomly drawn out from it. Find the probability that ball drawn is white.
. Then a ball is randomly drawn out from it. Find the probability that ball drawn is white.
As per the given question,
A factory has two machines  and
and  . Past records show that the machine
. Past records show that the machine  produced
produced 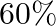 of the items of output and machine
of the items of output and machine  produced
produced 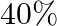 of the items. Further
of the items. Further 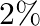 of the items produced by machine
of the items produced by machine  were defective and
were defective and 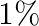 produced by machine
produced by machine  were defective. If an item is drawn at random, what is the probability that it is defective?
were defective. If an item is drawn at random, what is the probability that it is defective?
As per the given question,
An unbiased coin is tossed. If the result is a head, a pair of unbiased dice is rolled and the sum of the numbers obtained is noted. If the result is a tail, a card from a well shuffled pack of eleven cards numbered 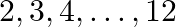 is picked and the number on the card is noted. What is the probability that the noted number is either 7 or 8 ?
is picked and the number on the card is noted. What is the probability that the noted number is either 7 or 8 ?
An unbiased coin is tossed, then I:- If head occurs, a pair of dice is rolled and sum on them is either $7$ or $8.$ II:- If tail occurs, a card is drawn from cards number $2,3,....12$ and is $7$ or...
The contents of three bags I, II and III are as follows: Bag I: 1 white, 2 black and 3 red balls, Bag II: 2 white, 1 black and 1 red, and Bag III: 4 white, 5 black and 3 red balls. A bag is chosen at random and two balls are drawn. What is the probability that the balls are white and red?
As per the given question,
A bag contains 3 white and 2 black balls and another bag contains 2 white and 4 black balls. One bag is chosen at random. From the selected bag, one ball is drawn. Find the probability that the ball drawn is white.
As per the given question,
One bag contains 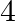 yellow and
yellow and 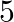 red balls. Another bag contains
red balls. Another bag contains 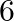 yellow and
yellow and 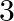 red balls. A ball is transferred from the first bag to the second bag and then a ball is drawn from the second bag. Find the probability that the ball drawn is yellow.
red balls. A ball is transferred from the first bag to the second bag and then a ball is drawn from the second bag. Find the probability that the ball drawn is yellow.
Given, $Bag\;I$ contains $4$ yellow and $5$ red balls $Bag\;II$ contains $6$ yellow and $3$ red balls Now, there are two ways of transferring a ball from $bag\;I\;to\;bag\;II$ $Way – 1$ By...
A purse contains 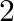 silver and
silver and 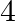 copper coins. A second purse contains
copper coins. A second purse contains 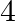 silver and
silver and 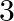 copper coins. If a coin is pulled at random from one of the two purses, what is the probability that it is a silver coin?
copper coins. If a coin is pulled at random from one of the two purses, what is the probability that it is a silver coin?
As per the given question,
A bag A contains 5 white and 6 black balls. Another bag B contains 4 white and 3 black balls. A ball is transferred from bag A to the bag B and then a ball is taken out of the second bag. Find the probability of this ball being black.
A black ball can be drawn in two mutually exclusive ways: (I) By transferring a white ball from bag A to bag B, then drawing a black ball (II) By transferring a black ball from bag A to bag B, then...
In a hockey match, both teams  and
and  scored same number of goals upto the end of the game, so to decide the winner, the refree asked both the captains to throw a die alternately and decide that the team, whose captain gets a first six, will be declared the winner. If the captain of team
scored same number of goals upto the end of the game, so to decide the winner, the refree asked both the captains to throw a die alternately and decide that the team, whose captain gets a first six, will be declared the winner. If the captain of team  was asked to start, find their respective probabilities of winning the match and state whether the decision of the refree was fair or not.
was asked to start, find their respective probabilities of winning the match and state whether the decision of the refree was fair or not.
As per the given question,
Out of 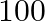 students, two sections of
students, two sections of 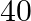 and
and 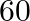 are formed. If you and your friend are among 100 students, what is the probability that: (i) you both enter the same section? (ii) you both enter the different section?
are formed. If you and your friend are among 100 students, what is the probability that: (i) you both enter the same section? (ii) you both enter the different section?
As per the given question,
A card is drawn from a well-shuffled deck of 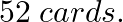 The outcome is noted, the card is replaced and the deck reshuffled. Another card is then drawn from the deck. (i) What is the probability that both the cards are of the same suit? (ii) What is the probability that the first card is an ace and the second card is a red queen?
The outcome is noted, the card is replaced and the deck reshuffled. Another card is then drawn from the deck. (i) What is the probability that both the cards are of the same suit? (ii) What is the probability that the first card is an ace and the second card is a red queen?
As per the given question,
An urn contains 7 red and 4 blue balls. Two balls are drawn at random with replacement. Find the probability of getting one red and one blue ball.
As per the given question,
An urn contains 7 red and 4 blue balls. Two balls are drawn at random with replacement. Find the probability of getting (i) 2 red balls (ii) 2blue balls
As per the given question,
A bag contains 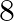 marbles of which
marbles of which 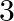 are blue and
are blue and 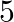 are red. one marble is drawn at random, its colour is noted and the marble is replaced in the bag. A marble is again drawn from the bag and its colour is noted. Find the probability that the marble will be Of the same colour.
are red. one marble is drawn at random, its colour is noted and the marble is replaced in the bag. A marble is again drawn from the bag and its colour is noted. Find the probability that the marble will be Of the same colour.
Bag contains blue, red marbles. One marble is drawn, its colour noted and replaced, then again a marble drawn and its colour noted.
A bag contains 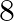 marbles of which
marbles of which 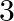 are blue and
are blue and 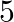 are red. one marble is drawn at random, its colour is noted and the marble is replaced in the bag. A marble is again drawn from the bag and its colour is noted. Find the probability that the marble will be (i) blue followed by red. (ii) blue and red in any order.
are red. one marble is drawn at random, its colour is noted and the marble is replaced in the bag. A marble is again drawn from the bag and its colour is noted. Find the probability that the marble will be (i) blue followed by red. (ii) blue and red in any order.
Bag contains $3$ blue, $5$ red marbles. One marble is drawn, its colour noted and replaced, then again a marble drawn and its colour noted.
Fatima and John appear in an interview for two vacancies in the same post. The probability of Fatima’s selection is 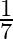 and that of John’s selection is
and that of John’s selection is 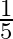 . What is the probability that none of them will be selected?
. What is the probability that none of them will be selected?
As per the given question,
Fatima and John appear in an interview for two vacancies in the same post. The probability of Fatima’s selection is 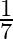 and that of John’s selection is
and that of John’s selection is 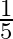 . What is the probability that (i) both of them will be selected? (ii) only one of them will be selected?
. What is the probability that (i) both of them will be selected? (ii) only one of them will be selected?
As per the given question,
There are 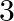 red and
red and 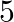 black balls in bag ‘
black balls in bag ‘ 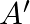 and
and 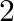 red and
red and 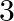 black balls in bag ‘
black balls in bag ‘ 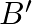 . one ball is drawn from bag ‘
. one ball is drawn from bag ‘ 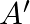 and two from bag ‘
and two from bag ‘ 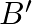 . Find the probability that out of the
. Find the probability that out of the 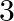 balls drawn one is red and
balls drawn one is red and 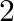 are black.
are black.
As per the given question,
 and
and  take turns in throwing two dice, the first to throw 10 being awarded the prize, show that if
take turns in throwing two dice, the first to throw 10 being awarded the prize, show that if  has the first throw, their chance of winning are in the ratio
has the first throw, their chance of winning are in the ratio 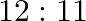 .
.
As per the given question,
Three persons 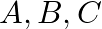 throw a die in succession till one gets a ‘six’ and wins the game. Find their respective probabilities of winning.
throw a die in succession till one gets a ‘six’ and wins the game. Find their respective probabilities of winning.
As per the given question,
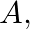
 and
and  in order toss a coin. The one to throw a head wins. What are their respective chances of winning assuming that the game may continue indefinitely?
in order toss a coin. The one to throw a head wins. What are their respective chances of winning assuming that the game may continue indefinitely?
As per the given question,
 and
and  take tums in throwing two dice, the first to throw
take tums in throwing two dice, the first to throw 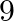 being awarded the prize. Show that their chance of winning are in the ratio
being awarded the prize. Show that their chance of winning are in the ratio 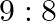 .
.
As per the given question,
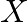 is taking up subjects – Mathematics, Physics and Chemistry in the examination. His probabilities of getting grade
is taking up subjects – Mathematics, Physics and Chemistry in the examination. His probabilities of getting grade  in these subjects are
in these subjects are 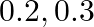 and
and 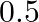 respectively. Find the probability that he gets. Grade
respectively. Find the probability that he gets. Grade  in two subjects.
in two subjects.
As per the given question,
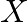 is taking up subjects – Mathematics, Physics and Chemistry in the examination. His probabilities of getting grade
is taking up subjects – Mathematics, Physics and Chemistry in the examination. His probabilities of getting grade  in these subjects are
in these subjects are 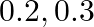 and
and 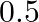 respectively. Find the probability that he gets. (i) Grade
respectively. Find the probability that he gets. (i) Grade  in all subjects (ii) Grade
in all subjects (ii) Grade  in no subject
in no subject
As per the given question,
There are three urns 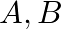 and
and  . Urn
. Urn  contains
contains 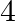 red balls and
red balls and 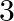 black balls. Urn
black balls. Urn  contains
contains 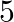 red balls and
red balls and 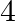 black balls. Urn
black balls. Urn  contains
contains 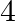 red and
red and 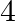 black balls. One ball is drawn from each of these urns. What is the probability that
black balls. One ball is drawn from each of these urns. What is the probability that 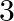 balls drawn consist of
balls drawn consist of 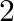 red balls and a black ball?
red balls and a black ball?
As per the given question,
The probability of student  passing an examination is
passing an examination is 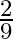 and of student
and of student  passing is
passing is 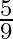 . Assuming the two events: ‘
. Assuming the two events: ‘  passes’, ‘
passes’, ‘  passes as independent, find the probability of : (i) only A passing the examination (ii) only one of them passing the examination.
passes as independent, find the probability of : (i) only A passing the examination (ii) only one of them passing the examination.
As per the given question,
A can hit a target 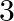 times in
times in 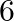 shots,
shots, 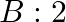 times in
times in 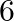 shots and
shots and 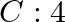 times in
times in 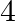 shots. They fix a volley. What is the probability that at least 2 shots hit?
shots. They fix a volley. What is the probability that at least 2 shots hit?
As per the given question,
A bag contains 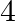 red and
red and 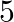 black balls, a second bag contains
black balls, a second bag contains 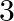 red and
red and 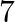 black balls. One ball is drawn at random from each bag; find the probability that the (i) balls are of different colours (ii) balls are of the same colour.
black balls. One ball is drawn at random from each bag; find the probability that the (i) balls are of different colours (ii) balls are of the same colour.
As per the given question,
Three cards are drawn with replacement from a well shuffled pack of cards. Find the probability that the cards are a king, a queen and a jack.
As per the given question,
A bag contains 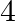 white,
white, 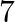 black, and
black, and 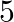 red balls. 4 balls are drawn with replacement What is the probability that at least two are white?
red balls. 4 balls are drawn with replacement What is the probability that at least two are white?
As per the given question,
A bag contains 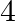 white balls and
white balls and 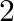 black balls. Another contains 3 white balls and 5 black balls. If one ball is drawn from each bag, find the probability that One is white and one is black.
black balls. Another contains 3 white balls and 5 black balls. If one ball is drawn from each bag, find the probability that One is white and one is black.
As per the given question,
A bag contains 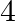 white balls and
white balls and 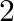 black balls. Another contains 3 white balls and 5 black balls. If one ball is drawn from each bag, find the probability that (i) Both are white (ii) Both are black
black balls. Another contains 3 white balls and 5 black balls. If one ball is drawn from each bag, find the probability that (i) Both are white (ii) Both are black
As per the given question,
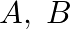 , and
, and  are independent witness of an event which is known to have occurred.
are independent witness of an event which is known to have occurred.  speaks the truth three times out of four,
speaks the truth three times out of four,  four times out of five and
four times out of five and  five times out of six. What is the probability that the occurrence will be reported truthfully by majority of three witnesses?
five times out of six. What is the probability that the occurrence will be reported truthfully by majority of three witnesses?
As per the given question,
A bag contains 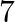 white,
white, 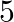 black and
black and 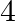 red balls. Four balls are drawn without replacement. Find the probability that at least three balls are black.
red balls. Four balls are drawn without replacement. Find the probability that at least three balls are black.
As per the given question,
A husband and wife appear in an interview for two vacancies in the same post. The probability of husband’s selection is 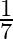 and that of wife’s selection is
and that of wife’s selection is 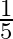 . What is the probability that none of them will be selected?
. What is the probability that none of them will be selected?
As per the given question,
A husband and wife appear in an interview for two vacancies in the same post. The probability of husband’s selection is 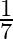 and that of wife’s selection is
and that of wife’s selection is 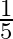 . What is the probability that (a) both of them will be selected? (b) only one of them will be selected?
. What is the probability that (a) both of them will be selected? (b) only one of them will be selected?
As per the given question,
In a family, the husband tells a lie in 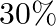 cases and the wife in
cases and the wife in 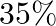 cases. Find the probability that both contradict each other on the same fact.
cases. Find the probability that both contradict each other on the same fact.
As per the given question,
Tickets are numbered from 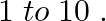 Two tickets are drawn one after the other at random. Find the probability that the number on one of the tickets is a multiple of
Two tickets are drawn one after the other at random. Find the probability that the number on one of the tickets is a multiple of 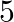 and on the other a multiple of
and on the other a multiple of 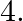
As per the given question,
Two cards are drawn from a well shuffled pack of 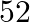 cards, one after another without replacement. Find the probability that one of these is red card and the other a black card?
cards, one after another without replacement. Find the probability that one of these is red card and the other a black card?
As per the given question,
 and
and  toss a coin alternately till one of them gets a head and wins the game, If
toss a coin alternately till one of them gets a head and wins the game, If  starts the game, find the probability that
starts the game, find the probability that  will win the game.
will win the game.
As per the given question,
Arun and Tarun appeared for an interview for two vacancies. The probability of Arun’s selection is 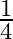 and that of Tarun’s rejection is
and that of Tarun’s rejection is 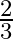 . Find the probability that at least and of them will be selected.
. Find the probability that at least and of them will be selected.
As per the given question,
A bag contains 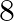 red and
red and 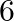 green balls. Three balls are drawn one after another without replacement. Find the probability that at least two balls drawn are green.
green balls. Three balls are drawn one after another without replacement. Find the probability that at least two balls drawn are green.
As per the given question,
A bag contains 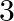 white,
white, 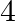 red and
red and 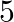 black balls. Two balls are drawn one after the other, without replacement. What is the probability that one is white and the other is black?
black balls. Two balls are drawn one after the other, without replacement. What is the probability that one is white and the other is black?
As per the given question,
Kamal and Monica appeared for an interview for two vacancies. The probability of Kamal’s selection is 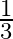 and that of Monika’s selection is
and that of Monika’s selection is 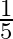 . Find the probability that (i) at least one of them will be selected (ii) only one of them will be selected.
. Find the probability that (i) at least one of them will be selected (ii) only one of them will be selected.
As per the given question, (i) (ii)
Kamal and Monica appeared for an interview for two vacancies. The probability of Kamal’s selection is 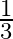 and that of Monika’s selection is
and that of Monika’s selection is 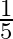 . Find the probability that
. Find the probability that 
As per the given question,
A speaks truth in 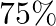 and
and  in
in 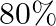 of the cases. In what percentage of cases are they likely to contradict each other in narrating the same incident?
of the cases. In what percentage of cases are they likely to contradict each other in narrating the same incident?
As per the given question,
Two cards are drawn successively without replacement from a well-shuffled deck of cards. Find the probability of exacty one ace.
As per the given question,
Two balls are drawn at random with replacement from a box containing 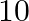 black and
black and 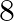 red balls. Find the probability that one of them is black and other is red.
red balls. Find the probability that one of them is black and other is red.
As per the given question,
Two balls are drawn at random with replacement from a box containing 10 black and 8 red balls. Find the probability that (i) both the ball are red (ii) first ball is black and second is red.
As per the given question,
A bag contains 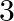 red and
red and 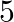 black balls and a second bag contains
black balls and a second bag contains 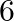 red and
red and 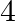 black balls. A ball is drawn from each bag. Find the probability that one is red and the other is black.
black balls. A ball is drawn from each bag. Find the probability that one is red and the other is black.
As per the given question,
A bag contains 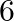 black and
black and 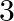 white balls. Another bag contains
white balls. Another bag contains 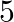 black and
black and 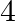 white balls. If one ball is drawn from each bag, find the probability that these two balls are of the same color.
white balls. If one ball is drawn from each bag, find the probability that these two balls are of the same color.
As per the given question,
Let  and
and  be two independent events such that
be two independent events such that  and
and 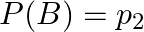 . Describe in words the events whose probabilities are
. Describe in words the events whose probabilities are 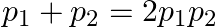
Events are said to be independent, if the occurrence or non – occurrence of one does not affect the probability of the occurrence or non – occurrence of the other.
Let  and
and  be two independent events such that
be two independent events such that  and
and 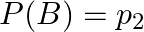 . Describe in words the events whose probabilities are
. Describe in words the events whose probabilities are 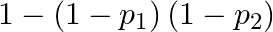
Events are said to be independent, if the occurrence or non – occurrence of one does not affect the probability of the occurrence or non – occurrence of the other.
Let  and
and  be two independent events such that
be two independent events such that  and
and 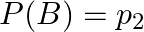 . Describe in words the events whose probabilities are (i)
. Describe in words the events whose probabilities are (i) 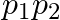 (ii)
(ii) 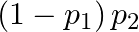
Events are said to be independent, if the occurrence or non - occurrence of one does not affect the probability of the occurrence or non - occurrence of the other.
Two dice are thrown together and the total score is noted. The event 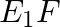 and
and 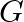 are “a total
are “a total 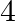 “, “a total of
“, “a total of 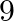 or more” and “a total divisible by
or more” and “a total divisible by 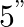 , respectively. Calculate
, respectively. Calculate 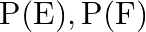 and
and 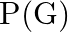 and decide which pairs of events, if any, are independent.
and decide which pairs of events, if any, are independent.
As per the given question,
The probabilities of two students 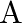 and
and 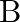 coming to the school in time are
coming to the school in time are 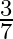 and
and 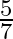 respectively. Assuming that the events, ‘A coming in time’ and ‘B coming in time’ are independent, find the probability of only one of them coming to the school in time. Write at least one advantage of coming to school in time.
respectively. Assuming that the events, ‘A coming in time’ and ‘B coming in time’ are independent, find the probability of only one of them coming to the school in time. Write at least one advantage of coming to school in time.
Given that the events 'A coming in time' and 'B coming in time' are independent. The advantage of coming to school in time is that you will not miss any part of the lecture and will be able to learn...
An urn contains 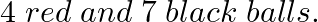 Two balls are drawn at random with replacement. Find the probability of getting one red and one blue ball.
Two balls are drawn at random with replacement. Find the probability of getting one red and one blue ball.
As per the given question,
An urn contains 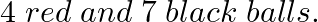 Two balls are drawn at random with replacement. Find the probability of getting
Two balls are drawn at random with replacement. Find the probability of getting 
As per the given question,
Two balls are drawn at random with replacement from a box containing 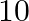 black and
black and 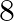 red balls. Find the probability that one of them is black and other is red
red balls. Find the probability that one of them is black and other is red
As per the given question,
Two balls are drawn at random with replacement from a box containing 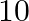 black and
black and 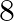 red balls. Find the probability that (i) Both balls are red (ii) First ball is black and second is red.
red balls. Find the probability that (i) Both balls are red (ii) First ball is black and second is red.
As per the given question,
A die is thrown thrice. Find the probability of getting an odd number at least once.
As per the given question,
The odds against a certain event are 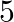 to
to 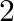 and the odds in favour of another event, independent to the former are 6 to 5 . Find the probability that (a) at least one of the events will occur, and (b) none of the events will occur.
and the odds in favour of another event, independent to the former are 6 to 5 . Find the probability that (a) at least one of the events will occur, and (b) none of the events will occur.
As per the given question,
An anti-aircraft gun can take a maximum of 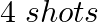 at an enemy plane moving away from it. The probabilities of hitting the plane at the first, second, third and fourth shot are
at an enemy plane moving away from it. The probabilities of hitting the plane at the first, second, third and fourth shot are 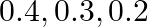 and
and 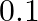 respectively. What is the probability that the gun hits the plane?
respectively. What is the probability that the gun hits the plane?
As per the given question,
The probability that  hits a target is
hits a target is 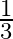 and the probability that
and the probability that  hits it, is
hits it, is 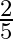 What is the probability that the target will be hit, if each one of
What is the probability that the target will be hit, if each one of  and
and  shoots at the target?
shoots at the target?
As per the given question,
An article manufactured by a company consists of two parts 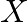 and
and 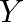 . In the process of manufacture of the part
. In the process of manufacture of the part  out of
out of 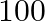 parts may be defective. Similarly,
parts may be defective. Similarly, 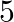 out of
out of 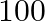 are likely to be defective in the manufacture of part
are likely to be defective in the manufacture of part 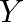 . Calculate the probability that the assembled product will not be defective.
. Calculate the probability that the assembled product will not be defective.
As per the given question,
Three cards are drawn with replacement from a well shuffled pack of cards. Find the probability that the cards drawn are king, queen and jack.
As per the given question,
A bag contains 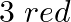 and
and 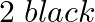 balls. One ball is drawn from it at random. Its color is noted and then it is put back in the bag. A second draw is made and the same procedure is repeated. Find the probability of drawing first red and second black ball.
balls. One ball is drawn from it at random. Its color is noted and then it is put back in the bag. A second draw is made and the same procedure is repeated. Find the probability of drawing first red and second black ball.
As per the given question,
A bag contains 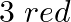 and
and 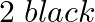 balls. One ball is drawn from it at random. Its color is noted and then it is put back in the bag. A second draw is made and the same procedure is repeated. Find the probability of drawing (i) two red balls, (ii) two black balls
balls. One ball is drawn from it at random. Its color is noted and then it is put back in the bag. A second draw is made and the same procedure is repeated. Find the probability of drawing (i) two red balls, (ii) two black balls
As per the given question,
An unbiased die is tossed twice. Find the probability of getting 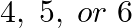 on the first toss and
on the first toss and 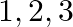 or 4 on the second toss.
or 4 on the second toss.
As per the given question,
Given the probability that  can solve a problem is
can solve a problem is 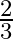 and the probability that
and the probability that  can solve the same problem is
can solve the same problem is 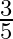 . Find the probability that none of the two will be able to solve the problem.
. Find the probability that none of the two will be able to solve the problem.
As per the given question,
A die is tossed twice. Find the probability of getting a number greater than 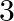 on each toss.
on each toss.
As per the given question,
If  and
and  are two independent events such that
are two independent events such that 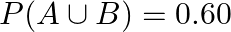 and
and 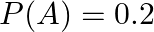 find
find 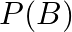
As per the given question,
 and
and  are two independent events. The probability that
are two independent events. The probability that  and
and  occur is
occur is 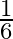 and the probability that neither of them oocurs is
and the probability that neither of them oocurs is 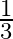 . Find the probability of occurrence of two events.
. Find the probability of occurrence of two events.
As per the given question, ......(i)
If  and
and  are two independent events such that
are two independent events such that 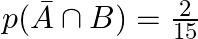 and
and 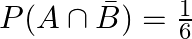 , then find
, then find 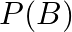 .
.
As per the given question,
If 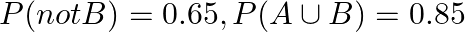 , and
, and  and
and  are independent events, then find
are independent events, then find 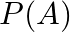 .
.
As per the given question,
Given two independent events  and
and  such that
such that 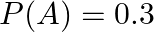 and
and 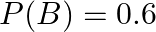 , Find
, Find 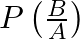
Given that $A\;and\;B$ are independent events and $P(A)\;=\;0.3,\; P(B)\;=\;0.6$
Given two independent events  and
and  such that
such that 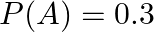 and
and 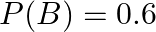 , Find (i)
, Find (i) 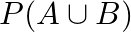 (ii)
(ii) 
Given that $A\;and\;B$ are independent events and $P(A)\;=\;0.3,\; P(B)\;=\;0.6$ (i) (ii)
Given two independent events  and
and  such that
such that 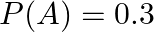 and
and 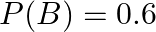 , Find
, Find 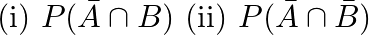
Given that $A\;and\;B$ are independent events and $P(A)\;=\;0.3,\; P(B)\;=\;0.6$ (i) (ii)
Given two independent events  and
and  such that
such that 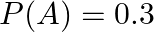 and
and 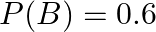 , Find
, Find 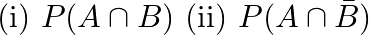
Given that $A\;and\;B$ are independent events and $P(A)\;=\;0.3,\; P(B)\;=\;0.6$
If  and
and  be two events such that
be two events such that 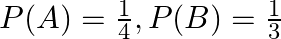 and
and 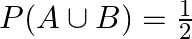 , show that
, show that  and
and  are independent events.
are independent events.
As per the given question,
A coin is tossed three times. Let the events 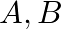 and
and  be defined as follows:
be defined as follows: 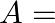 first toss is head,
first toss is head, 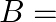 second toss is head, and
second toss is head, and 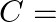 exactly two heads are tossed in a row.
exactly two heads are tossed in a row. 
As per the given question,
A coin is tossed three times. Let the events 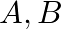 and
and  be defined as follows:
be defined as follows: 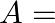 first toss is head,
first toss is head, 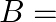 second toss is head, and
second toss is head, and 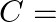 exactly two heads are tossed in a row.
exactly two heads are tossed in a row. 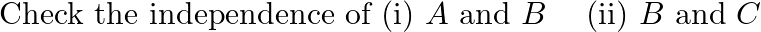
As per the given question,
A card is drawn from a pack of 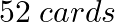 so that each card is equally likely to be selected. State whether events
so that each card is equally likely to be selected. State whether events  and
and  are independent if,
are independent if, 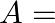 the card drawn is spade,
the card drawn is spade, 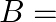 the card drawn in an ace
the card drawn in an ace
As per the given question,
(i) A card is drawn from a pack of 52 cards so that each card is equally likely to be selected. State whether events  and
and  are independent if,
are independent if, 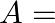 the card drawn is a king or queen
the card drawn is a king or queen 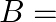 the card drawn is a queen or jack (ii) A card is drawn from a pack of 52 cards so that each card is equally likely to be selected. State whether events
the card drawn is a queen or jack (ii) A card is drawn from a pack of 52 cards so that each card is equally likely to be selected. State whether events  and
and  are independent if,
are independent if, 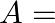 the card drawn is black,
the card drawn is black, 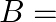 the card drawn is a king
the card drawn is a king
As per the given question, (i) (ii)
Prove that in throwing a pair of dice, the occurrence of the number 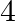 on the first die is independent of the occurrence of
on the first die is independent of the occurrence of 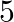 on the second die.
on the second die.
As per the given question,
A coin is tossed thrice and all the eight outcomes are assumed equally likely. State whether events  and
and  are independent if,
are independent if, 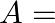 the number of heads is two,
the number of heads is two, 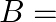 the last throw results in head
the last throw results in head
As per the given question,
(i) A coin is tossed thrice and all the eight outcomes are assumed equally likely. State whether events  and
and  are independent if,
are independent if, 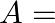 the first throw results in head,
the first throw results in head, 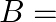 the last throw results in tail (ii) A coin is tossed thrice and all the eight outcomes are assumed equally likely. State whether events
the last throw results in tail (ii) A coin is tossed thrice and all the eight outcomes are assumed equally likely. State whether events  and
and  are independent if,
are independent if, 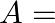 the number of heads is odd,
the number of heads is odd, 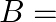 the number of tails is odd
the number of tails is odd
As per the given question, So, $A\;and\;B$ are independent events. (ii)
Assume that each born child is equally likely to be a boy or a girl. If a family has two children, what is the conditional probability that both are girls? Given that (i) the youngest is a girl (ii) at least one is girl.
As per the given question, (i) Let $'A'$ be the event that both the children born are girls. Let $'B'$ be the event that the youngest is a girl. We have to find conditional probability $P(A/B).$...
Ten cards numbered 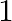 through
through 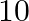 are placed in a box, mixed up thoroughly and then one card is drawn randomly. If it is known that the number on the drawn card is more than
are placed in a box, mixed up thoroughly and then one card is drawn randomly. If it is known that the number on the drawn card is more than 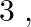 what is the probability that it is an even number?
what is the probability that it is an even number?
As per the given question,
In a school there are 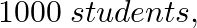 out of which
out of which 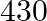 are girls. It is known that out of
are girls. It is known that out of 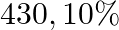 of the girls study in class
of the girls study in class  . What is the probability that a student chosen randomly studies in class
. What is the probability that a student chosen randomly studies in class  given that the chosen student is a girl?
given that the chosen student is a girl?
As per the given question,
