Answer: a) 7.5o The distance between the refracting surfaces is negligible with thin prisms, thus the prism angle (A) is very small. Because A = r1 + r2, if A is tiny, both r1 and r2 will be little...
A ray of light incident at an angle θ on a refracting face of a prism emerges from the other face normally. If the angle of the prism is 5o and the prism is made of a material of refractive index 1.5, the angle of incidence is
The velocity-displacement graph of a particle is shown in the figure. a) Write the relation between v and x. b) Obtain the relation between acceleration and displacement and plot it.
a) Consider the point P(x,v) at any time t on the graph such that angle ABO is θ such that tan θ = AQ/QP = (v0-v)/x = v0/x0 When the velocity decreases from v0 to zero during the displacement, the...
A man runs across the roof-top of a tall building and jumps horizontally with the hope of landing on the roof of the next building which is of a lower height than the first. If his speed is 9 m/s, the distance between the two buildings is 10 m and the height difference is 9 m, will he be able to land on the next building?
For a free fall at 9m, the horizontal distance covered by the man should be at least 10 m. u = 0 a = 10 m/s2 s = 9 m t = t s = ut + 1/2 at2 Substituting the values, we get t = √9/3 = 3/√5 sec The...
A ball is dropped and its displacement vs time graph is as shown in the figure where displacement x is from the ground and all quantities are positive upwards. a) Plot qualitatively velocity vs time graph b) Plot qualitatively acceleration vs time graph
a) At t=0 and v=0 , v-t graph is: b) At x = 0, a-t graph is:
A ball is dropped from a building of height 45 m. Simultaneously another ball is thrown up with a speed 40 m/s. Calculate the relative speed of the balls as a function of time.
V = v1 = ? U = 0 h = 45 m a = g t = t V = u + at v1 = 0 + gt v1 = gt Therefore, when the ball is thrown upward, v1 = -gt V = v2 u = 40 m/s a = g t = t V = u + at v2 = 40 – gt The relative velocity...
It is a common observation that rain clouds can be at about a kilometre altitude above the ground. a) If a rain drop falls from such a height freely under gravity, what will be its speed? Also, calculate in km/h b) A typical rain drop is about 4 mm diameter. Momentum is mass x speed in magnitude. Estimate its momentum when it hits ground. c) Estimate the time required to flatten the drop. d) Rate of change of momentum is force. Estimate how much force such a drop would exert on you. e) Estimate the order of magnitude force on umbrella. Typical lateral separation between two rain drops is 5 cm.
a) Velocity attained by the rain drop which is falling freely through the height h is: v2 = u2 – 2g(-h) As u = 0 v = √2gh = 100√2 m/s = 510 km/h b) Diameter of the drop, d = 2r = 4 mm Radius of the...
A motor car moving at a speed of 72 km/h cannot come to a stop in less than 3 s while for a truck this time interval is 5 s. On a highway the car is behind the truck both moving at 72 km/h. The truck gives a signal that it is going to stop at emergency. At what distance the car should be from the truck so that it does not bump onto the truck. Human response time is 0.5 s.
For truck, u = 20 m/s v = 0 a = ? t = 5s v = u + at a = 4 m/s2 For car, t = 3 s u = 20 m/s v = 0 a = ac v = u + at ac = -20/3 m/s2 Let s be the distance between the car and the truck when the truck...
A monkey climbs up a slippery pole for 3 seconds and subsequently slips for 3 seconds. Its velocity at time t is given by v(t) = 2t (3 – t); 0
a) For maximum velocity v(t) dv(t)/dt = 0 Substituting the value for v, we get t = 1.5 seconds b) For average velocity = total distance/time taken Average velocity = 3 m And the average velocity is...
A man is standing on top of a building 100 m high. He throws two balls vertically, one at t = 0 and other after a time interval. The later ball is thrown at a velocity of half the first. The vertical gap between first and second ball is +15m at t = 2s. The gap is found to remain constant. Calculate the velocity with which the balls were thrown and the exact time interval between their throw.
Let the speed of ball 1 = u1 = 2u m/s Then the speed of ball 2 = u2 = u m/s The height covered by ball 1 before coming to rest = h1 The height covered by ball 2 before coming to rest = h2 We know...
A bird is tossing between two cars moving towards each other on a straight road. One car has a speed of 18 m/h while the other has the speed of 27 km/h. The bird starts moving from first car towards the other and is moving with the speed of 36 km/h and when the two cars were separated by 36 km. What is the total distance covered by the bird? What is the total displacement of the bird?
The relative speed of the cars = 27 + 18 = 45 km/h When the two cars meet together, time t is given as t = distance between cars/relative speed of cars = 36/(27+18) t = 4/5 h Therefore, distance...
A particle executes the motion described by x(t) = x0 (1 – e-γt) where t ≥ 0, x0 > 0 a) Where does the particles start and with what velocity? b) Find maximum and minimum values of x(t), v(t), a(t). Show that x(t) and a(t) increase with time and v(t) decreases with time.
a) x(t) = x0 (1 – e-γt) v(t) = dx(t)/dt = +x0 γ e-γt a(t) = dv/dt = x0 γ2 e-γt v(0) = x0 γ b) x(t) is minimum at t = 0 since t = 0 and [x(t)]min = 0 x(t) is maximum at t = ∞ since t = ∞ and...
An object falling through a fluid is observed to have acceleration given by a = g – bv where g = gravitational acceleration and b is constant. After a long time of release, it is observed to fall with constant speed. What must be the value of constant speed?
The concept used in this question will be based on the behaviour of a spherical object when it is dropped through a viscous fluid. When a spherical body of radius r is dropped, it is first...
Give example of a motion where x>0, v<0, a>0 at a particular instant.
Let the motion be represented as: x(t) = A + Be– γ t Let A>B and γ >0 Velocity is x(t) = dx/dt = -Be– γ t Acceleration is a(t) = dx/dt = B γ 2e– γ t Therefore, it can be said that x(t) > 0,...
Give examples of a one-dimensional motion where a) the particle moving along positive x-direction comes to rest periodically and moves forward b) the particle moving along positive x-direction comes to rest periodically and moves backwardπ
When an equation has sine and cosine functions, the nature is periodic. a) When the particle is moving in positive x-direction, it is given as t > sin t When the displacement is as a function of...
A uniformly moving cricket ball is turned back by hitting it with a bat for a very short time interval. Show the variation of its acceleration with taking acceleration in the backward direction as positive.
The force which is generated by the bat is known as impulsive force. When the effect of gravity is ignored, it can be said that the ball moves with a uniform speed horizontally and returns back to...
Refer to the graphs below and match the following:
Graph Characteristics a) i) has v > 0 and a < 0 throughout b) ii) has x > 0 throughout and has a point with v = 0 and a point with a = 0 c) iii) has a point with zero displacement for t...
A ball is bouncing elastically with a speed 1 m/s between walls of a railway compartment of size 10 m in a direction perpendicular to walls. The train is moving at a constant velocity of 10 m/s parallel to the direction of motion of the ball. As seen from the ground, a) the direction of motion of the ball changes every 10 seconds b) speed of ball changes every 10 seconds c) average speed of ball over any 20 seconds intervals is fixed d) the acceleration of ball is the same as from the train
The correct option is b) speed of ball changes every 10 seconds, c) average speed of ball over any 20 seconds intervals is fixed, and d) the acceleration of the ball is the same as from the train
A spring with one end attached to a mass and the other to a rigid support is stretched and released. a) magnitude of acceleration, when just released is maximum b) magnitude of acceleration, when at equilibrium position is maximum c) speed is maximum when mass is at equilibrium position d) magnitude of displacement is always maximum whenever speed is minimum
The correct answer is a) magnitude of acceleration, when just released is maximum and c) speed is maximum when mass is at equilibrium position
For the one-dimensional motion, describe by x = t – sint a) x(t)>0 for all t>0 b) v(t)>0 for all t>0 c) a(t)>0 for all t>0 d) v(t) lies between 0 and 2
The correct answer is a) x(t)>0 for all t>0 and d) v(t) lies between 0 and 2
A graph of x versus t is shown in the figure. Choose correct alternatives from below. a) the particle was released from rest at t=0 b) at B, the acceleration a>0 c) at C, the velocity and the acceleration vanish d) average velocity for the motion A and D is positive e) the speed at D exceeds that at E
The correct answer is a) the particle was released from rest at t=0, c) at C, the velocity and the acceleration vanish and e) the speed at D exceeds that at E
The variation of quantity A with quantity B, plotted in figure describes the motion of a particle in a straight line. a) quantity B may represent time b) quantity A is velocity if motion is uniform c) quantity A is displacement if motion is uniform d) quantity A is velocity if motion is uniformly accelerated
The correct answer is a) quantity B may represent time, c) quantity A is displacement if motion is uniform, and d) quantity A is velocity if motion is uniformly accelerated
At a metro station, a girl walks up a stationary escalator in time t1. If she remains stationary on the escalator, then the escalator take her up in time t2. The time taken by her to walk up on the moving escalator will be a) (t1 + t2)/2 b) t1t2/(t2 – t1) c) t1t2/(t2 + t1) d) t1 – t2
The correct answer is c) t1t2/(t2 + t1)
The displacement of a particle is given by x = (t-2)2 where x is in metres and t is seconds. The distance covered by the particle in first 4 seconds is a) 4 m b) 8 m c) 12 m d) 16 m
The correct answer is b) 8 m
A vehicle travels half the distance L with speed V1 and the other half with speed V2, then its average speed is a) (V1+V2)/2 b) (2V1+V2)/(V1+V2) c) (2V1V2)/(V1+V2) d) L(V1+V2)/V1V2
The correct answer is c) (2V1V2)/(V1+V2)
A lift is coming from 8th floor and is just about to reach 4th floor. Taking ground floor as origin and positive direction upwards for all quantities, which one of the following is correct? a) x<0, v<0, a>0 b) x>0, v<0, a<0 c) x>0, v<0, a>0 d) x>0, v>0, a<0
The correct answer is a) x<0, v<0, a<0 The value of x and v becomes negative as the lift is moving from the 8th floor to the 4th floor whereas acceleration is acting upwards and stays...
Among the four graphs, there is only one graph for which average velocity over the time interval (0,T) can vanish for a suitably chosen T. Which one is it?
The correct answer is (b)
A helicopter of mass 2000 kg rises with a vertical acceleration of 15 m/s2. The total mass of the crew and passengers is 500 kg. Give the magnitude and direction of the a) force on the floor of the helicopter by the crew and passengers b) action of the rotor of the helicopter on the surrounding air c) force on the helicopter due to the surrounding air
Given, M = 2000 kg helicopter mass m = 500 kg m = 500 kg m = 500 kg m = 500 kg m = 500 kg m = 500 kg Helicopter acceleration with crew and passengers = 15 m/s2 a) Force exerted by the crew and...
A racing car travels on a track ABCDEFA. ABC is a circular arc of radius 2 R. CD and FA are straight paths of length R and DEF is a circular arc of radius R = 100 m. The coefficient of friction on the road is μ = 0.1. The maximum speed of the car is 50 m/s. Find the minimum time for completing one round.
Time taken from $A$ to $B$ to $C$ $\mathrm{S} 1=$ length $\mathrm{pf}$ path $=3 / 42 \pi(2 \mathrm{R})=300 \pi \mathrm{m}$ $\mathrm{V} 1=$ speed(maximum) along the circular path of the car $...
Below figures show (vx, t) and (vy, t) diagrams for a body of unit mass. Find the force as a function of time.
For graph a) $ \begin{array}{l} v_{x}=2 t \text { for } 0<t<1 s \\ a_{x}=2 / 1 \text { for } 0<t<1 s \\ v_{x}=2(2-t) \text { for } 1<t<2 s \\ a_{x}=-2 / 1=-2 \text { for }...
When a body slides down from rest along a smooth inclined plane making an angle of 45 degree with the horizontal, it takes time T. When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance, it is seen to take time pT, where p is some number greater than 1. Calculate the coefficient of friction between the body and the rough plane.
The inclined plane angle is $45^{\circ}$ such that $ \begin{array}{l} u=0 \\ s=s \\ t=T \\ a=g \sin 45^{\circ}=g / \sqrt{2} \\ s=u t+1 / 2 a t^{2} \\ s=g T^{2} / 2 \sqrt{2} \end{array} $ $...
A bock of mass M is held against a rough vertical wall by pressing it with a finger. If the coefficient of friction between the block and the wall is μ and the acceleration due to gravity is g, calculate the minimum force required to be applied by the ginger to hold the block against the wall?
F is the force exerted by the finger on a body of mass M that is resting on the wall. Using the balanced state as a starting point, $ \begin{array}{l} \mathrm{F}=\mathrm{N} \\ \mathrm{f}=\mathrm{Mg}...
Two masses of 5 kg and 3 kg are suspended with help of massless inextensible strings as shown in the figure. Calculate T1 and T2 when whole system is going upwards with acceleration = 2 m/s2.
The acceleration of the whole system is, $\mathrm{a}=2 \mathrm{~m} / \mathrm{s} 2$ $ \begin{array}{l} \mathrm{m} 1=5 \mathrm{~kg} \\ \mathrm{~m} 2=3 \mathrm{~kg} \\ \mathrm{~g}=9.8 \mathrm{~m} /...
Why does a child feel more pain when falls down on a hard cement floor, than when she falls on the soft muddy ground in the garden?
When a kid falls on a hard cement floor, the child feels more pain than when the child falls on soft muddy ground in the yard, since the time it takes the child to stop on the cemented ground is...
A block placed on a rough horizontal surface is pulled by a horizontal force F. Let f be the force applied by the rough surface on the block. Plot a graph of f versus F.
F1 is the force exerted on the heavy box, which is equal to F1 and is resisted by the lesser frictional force f1. F = Fs, which is the maximum static frictional force, is required for the box to...
The velocity of a body of mass 2 kg as a function of t is given by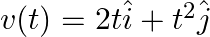 Find the momentum and the force acting on it at time t = 2 sec.
Find the momentum and the force acting on it at time t = 2 sec.
m=2kg $ \underset{v}{\rightarrow}(t)=2 t \hat{i}+t^{2} \hat{j} $ $ \vec{v} \text { at } 2 \mathrm{sec}, \underset{v}{\vec{v}}(2 t)=2(2 t) \hat{i} 2^{2} \hat{j}, v(2)=4 \hat{i}+4 \hat{j} $ $ \text {...
For the harmonic travelling wave y = 2 cos 2 π(10t-0.0080x+3.5) where x and y are in cm and t is second. What is the phase difference between the oscillatory motion at two points separated by a distance of
a) 4 m b) 0.5 m c) λ/2 d) 3 λ/4 e) what is the phase difference between the oscillation of a particle located at x = 100 cm at t = Ts and t = 5s? Answer: According to the questions, we have: y = 2...
In the given progressive waves y = 5 sin (100 πt – 0.4 πx) where y and x are in m, t is in s. What is the
a) amplitude b) wavelength Answer: According to the question, the wave is travelling in +x direction and the equation is given by; y = 5 sin (100 πt – 0.4 πx) The standard equation is as follows: y...
Given below are some functions of x and t to represent the displacement of an elastic wave.
a) y = 5 cos (4x) sin (20t) b) y = 4 sin (5x-t/2) + 3 cos (5x-t/2) c) y = 10 cos [(252-250)πt] cos [(252+250) πt] d) y = 100 cos (100 πt + 0.5x) State which of these represent a) a traveling wave...
If c is r.m.s speed of molecules in a gas and v is the speed of sound waves in the gas, show that c/v is constant and independent of temperature for all diatomic gases.
Answer: We know that the equation for molecules is: $ c=\sqrt{\frac{3RT}{M}} $ Where, M represents the molar mass of the gas $ v=\sqrt{\frac{\gamma P}{\rho }}=\sqrt{\frac{\gamma RT}{M}} $ We know...
The earth has a radius of 6400 km. The inner core of the 1000 km radius is solid. Outside it, there is a region from 1000 km to a radius of 3500 km which is in a molten state. Then again from 3500 km to 6400 km the earth is solid. Only longitudinal (P) waves can travel inside a liquid. Assume that the P wave has a speed of 8 km/s in solid parts and of 5 km/s in liquid parts of the earth. An earthquake occurs at someplace close to the surface of the earth. Calculate the time after which it will be recorded in a seismometer at a diametrically opposite point on the earth if wave travels along diameter?
Answer: According to the question, r1 = 1000 km, r2 = 3500 km, r3 = 6400 km and d1 = 1000 km And we can calculate, d2 = 3500 – 1000 d2 = 2500 km d3 = 6400 – 3500 d3 = 2900 km Expression for the...
Show that when a string fixed at its two ends vibrates in 1 loop, 2 loops, 3 loops, and 4 loops, the frequencies are in the ratio 1:2:3:4.
Answer: When n = 1, f1 = v/2L This is known as the fundamental frequency. When n = 2, f2 = 2(v/2L) This is known as the first overtone. When n = 3, f3 = 3(v/2L) This is known as the second overtone....
A tuning fork vibrating with a frequency of 512 Hz is kept close to the open end of a tube filled with water. The water level in the tube is gradually lowered. When the water level is 17 cm below the open end, the maximum intensity of sound is heard. If the room temperature is 20oC, calculate
c) if the water in the tube is replaced with mercury, will there be any difference in your observations? Answer: (c) Sound is reflected into the air column by water and mercury in the tube, forming...
A tuning fork vibrating with a frequency of 512 Hz is kept close to the open end of a tube filled with water. The water level in the tube is gradually lowered. When the water level is 17 cm below the open end, the maximum intensity of sound is heard. If the room temperature is 20oC, calculate
a) speed of sound in air at room temperature b) speed of sound in air at 0oC Answer: According to the question, the frequency of the tuning fork is f = 512 Hz a) When the first maxima are taken...
The pattern of standing waves formed on a stretched string at two instants of time are shown in the figure. The velocity of two waves superimposing to form stationary waves is 360 m/s and their frequencies are 256 Hz.
a) calculate the time at which the second curve is plotted b) mark nodes and antinodes on the curve c) calculate the distance between A’ and C’ Answer: According to the quetion, the frequency of the...
The wave pattern on a stretched string is shown in the figure. Interpret what kind of wave this is and find its wavelength.
Answer: A stationary wave which is at its mean position when the particles at t = T/4 and 3T/4 are at rest. The displacement of medium particles at distances of 10, 20, 30, 40, and 50 cm is always...
A train standing at the outer signal of a railway station blows a whistle of frequency 400 Hz still air. The train beings to move with a speed of 10 m/s towards the platform. What is the frequency of the sound for an observer standing on the platform?
Answer: It is given that v0 = 400 Hz and vz = 10 m/s We know that the velocity of sound in air is va = 330 m/s The frequency heard by the observer on the platform is v'. Therefore, we can write: v’...
A pipe of 20 cm long is closed at one end. Which harmonic mode of the pipe is resonantly excited by a source of 1237.5 Hz?
Answer: According to the question, the length is: l = 20 cm =0.2 m and the frequency is, v = 1237.5 Hz We know that the velocity of sound in air = 330 m/s The following expression is: l = λ/4 λ = 4l...
A steel wire has a length of 12 m and a mass of 2.10 kg. What will be the speed of a transverse wave on this wire when a tension of 2.06 × 104 N is applied?
Answer: According to the question, the length is, l = 12 m and the total mass, M = 2.10 kg Mass per unit length is given by7 m = M/l = 2.1/12 and we know that tension si: T = 2.06 × 104 N Therefore,...
When two waves of almost equal frequencies v1 and v2 reach at a point simultaneously, what is the time interval between successive maxima?
Answer: Beats are created when two waves of nearly identical frequency arrive at the same location at the same time. It is given that the two frequencies are almost equal, that is v1 = v2. And for...
At what temperatures will the speed of sound in air be 3 times its value at 0 degreesC?
Answer: Speed of sound in air is $ v=\sqrt{\frac{\gamma RT}{M}} $ where 'T' represents the absolute temperature. since both γ and M are constant, we can write: $ \therefore v\alpha \sqrt{T} $ $...
A sitar wire is replaced by another wire of same length and material but of three times earlier radius. If the tension in the wire remains the same, by what factor will the frequency change?
Answer: The wire is stretched both from the end so the frequency of stretched wire is as follows: $ v=\frac{n}{2L}\sqrt{\frac{T}{m}} $ As the number of harmonic n, length L, and tension (T) are kept...
The displacement of an elastic wave is given by the function y = 3 sin ωt + 4 cos ωt where y is in cm and t is in second. Calculate the resultant amplitude.
Answer: According to the question, y = 3 sin ωt + 4 cos ωt Let’s suppose that 3 = a cos φ and 4 = a sin φ Then, the equation becomes: y = a cos φ ωt + a sin φ ωt y = a sin (ωt + φ) tan φ = 4/3 φ =...
An organ pipe of length L open at both ends is found to vibrate in its first harmonic when sounded with a tuning fork of 480 Hz. What should be the length of a pipe closed at one end, so that it also vibrates in its first harmonic with the same tuning fork?
Answer: Because the medium, frequency, and number of harmonics are the same in open and closed pipes, the number of nodes and (wave) will be the same in both circumstances. When the harmonic is...
A sonometer wire is vibrating in resonance with a tuning fork. Keeping the tension applied same, the length of the wire is doubled. Under what conditions would the tuning fork still be is resonance with the wire?
Answer: When a sonometer vibrates, the length of the wire is doubled. The sonometer will resonate at 2L if the tuning fork resonates at L. The frequency of the sonometer is expressed using the...
A tuning fork A, marked 512 Hz, produces 5 beats per second, where sounded with another unmarked tuning fork B. If B is loaded with wax the number of beats is again 5 per second. What is the frequency of the tuning fork B when not loaded?
Answer: When the tuning fork B is loaded with wax, the tuning fork's frequency falls below its original frequency. Let's say that when the tuning fork is marked 512 Hz, the tuning fork B is marked...
Which of the following statements are true for a stationary wave?
a) every particle has a fixed amplitude which is different from the amplitude of its nearest particle b) all the particles cross their mean position at the same time c) all the particles are...
A train, standing in a station yard, blows a whistle of frequency 400 Hz in still air. The wind starts blowing in the direction from the yard to the station with a speed of 10 m/s. Given that the speed of sound in still air is 340 m/s
a) the frequency of sound as heard by an observer standing on the platform is 400 Hz b) the speed of sound for the observer standing on the platform is 350 m/s c) the frequency of sound as heard by...
The transverse displacement of a string is given by y(x,t) = 0.06 sin (2πx/3) cos (120πt). All the points on the string between two consecutive nodes vibrate with
a) same frequency b) same phase c) same energy d) different amplitude Answer: The correct answers are a) same frequency b) same phase d) different amplitude Explanation: This is the standing wave...
During propagation of a plane progressive mechanical wave
a) all the particles are vibrating in the same phase b) amplitude of all the particles is equal c) particles of the medium executes SHM d) wave velocity depends upon the nature of the medium Answer:...
Speed of sound waves in a fluid depends upon
a) directly on the density of the medium b) square of bulk modulus of the medium c) inversely on the square root of density d) directly on the square root of bulk modulus of the medium Answer: The...
The displacement of a string is given by y(x,t) = 0.06 sin (2πx/3) cos (120πt) where x and y are in m and t in s. The length of the string is 1.5 m and its mass is 3.0 × 10-2kg.
a) it represents a progressive wave of frequency 60 Hz b) it represents a stationary wave of frequency 60 Hz c) it is the result of the superposition of two waves of wavelength 3 m, frequency 60 Hz...
A transverse harmonic wave on a string is described by y (x,t) = 3.0 sin (36t + 0.018x + π/4) where x and y are in cm and t is in s. The positive direction of x is from left to right
a) the wave is travelling from right to left b) the speed of the wave is 20 m/s c) frequency of the wave is 5.7 Hz d) the least distance between two successive crests in the wave is 2.5 cm Answer:...
A train whistling at constant frequency is moving towards a station at a constant speed V. The train goes past a stationary observer on the station. The frequency n’ of the sound as heard by the observer is plotted as a function of time t. Identify the expected curve
Answer: The correct option is c) Explanation: Apparent Frequency can be expressed in a variety of ways. Assume that the observer (O) and the source (S) are both traveling in the same direction down...
A string of mass 2.5 kg is under a tension of 200 N. The length of the stretched string is 20.0 m. If the transverse jerk is struck at one end of the string, the disturbance will reach the other end in
a) one second b) 0.5 second c) 2 seconds d) data given is insufficient Answer: The correct option is b) 0.5 second Explanation: According to the question, m=2.50 kg, l = 20 m and T=200N $ \mu...
Equation of a plane progressive wave is given by y = 0.6 sin 2π(t-x/2). On reflection from a denser medium, its amplitude becomes 2/3 of the amplitude of the incident wave
a) y = 0.6 sin 2π(t+x/2) b) y = -0.4 sin 2π(t+x/2) c) y = 0.4 sin 2π(t+x/2) d) y = -0.4 sin 2π(t-x/2) Answer: The correct option is b) y = -0.4 sin 2π(t+x/2) Explanation: The amplitude of the...
A sound wave is passing through the air column in the form of compression and rarefaction. In consecutive compressions and rarefactions,
a) density remains constant b) Boyle’s law is obeyed c) bulk modulus of air oscillates d) there is no transfer of heat Answer: The correct option is d) there is no transfer of heat Explanation:...
Which of the following statements are true for wave motion?
a) mechanical transverse waves can propagate through all mediums b) longitudinal waves can propagate through solids only c) mechanical transverse waves can propagate through solids only d)...
With the propagation of longitudinal waves through a medium, the quantity transmitted is
a) matter b) energy c) energy and matter d) energy, matter, and momentum Answer: The correct option is b) energy The transfer of energy across a medium is caused by longitudinal waves propagating...
Change in temperature of the medium changes
a) frequency of sound waves b) amplitude of sound waves c) wavelength of sound waves d) loudness of sound waves Answer: The correct option is c) wavelength of sound waves Explanation: The velocity...
Speed of sound wave in air
a) is independent of temperature b) increases with pressure c) increases with an increase in humidity d) decreases with an increase in humidity Answer: The correct option is c) increases with an...
Sound waves of wavelength λ travelling in a medium with a speed of v m/s enter into another medium where its speed is 2v m/s. The wavelength of sound waves in the second medium is
a) λ b) λ/2 c) 2 λ d) 4 λ Answer: The correct answer is c) 2 λ Explanation: According to the question, the wavelength of sound waves in the first medium, λ = u/v ...
Water waves produced by a motorboat sailing in water are
a) neither longitudinal nor transverse b) both longitudinal and transverse c) only longitudinal d) only transverse Answer: The correct option is b) both longitudinal and transverse Let's...
A simple pendulum of time period 1s and length l is hung from a fixed support at O, such that the bob is at a distance H vertically above A on the ground. The amplitude is θo. The string snaps at θ = θ0/2. Find the time taken by the bob to hit the ground. Also, find the distance from A where bob hits the ground. Assume θ0 to be small so that sin θo, θo and cos θ0 1.
Answer: At t = t1 and θ= θ0/a We have, T = 1 sec θ0/2 = θ0 cos 2π/T t1 d θ/dt = – θ0 2π sin 2πt At t = 1/6, that is when θ = θ0/2 d θ/dt = – θ0π√3 v/l = – θ0π√3 v = -θ0π√3l θ0l [1/2 – π√6H/g] gives...
A tunnel is dug through the centre of the earth. Show that a body of mass ‘m’ when dropped from rest from one end of the tunnel will execute simple harmonic motion.
Answer: Let g’ be the acceleration due to gravity of the earth inside the earth g’ = g(1-d/R) R-d = y g’ = g y/R F = -mg y/R F is proportional to (-y) The motion is SHM when the body is in a tunnel....
One end of a V-tube containing mercury is connected to a suction pump and the other end to the atmosphere. The two arms of the tube are inclined to horizontal at an angle of 45o each. A small pressure difference is created between two columns when the suction pump is removed. Will the column of mercury in V-tube execute simple harmonic motion? Neglect capillary and viscous forces. Find the time period of oscillation.
Answer: Let h0 be the initial height of the columns and dx represent the element that needs to be considered Then the mass is given by: dm = A.dx.ρ Potential energy on the left of dm = (dm)gh Total...
A cylindrical log of wood of height h and area of cross-section A floats in water. It is pressed and then released. Show that the log would execute SHM with a time period where m is mass of the body and ρ is the density of the liquid.
Answer: Let us consider that the verticle displacement at the equilibrium position is $ {{x}_{0}} $ At equilibrium mg = Buoyant Force = $ A{{x}_{0}}\rho g $ When it is displaced further by a...
A body of mass m is attached to one end of a massless spring which is suspended vertically from a fixed point. The mass is held in hand so that the spring is neither stretched nor compressed. Suddenly the support of the hand is removed. The lowest position attained by the mass during oscillation is 4 cm below the point, where it was held in hand.
a) what is the amplitude of oscillation? b) find the frequency of oscillation? Answer: The mass m will oscillate between the lowest and the highest point, which is where it was held in hand. As a...
A person normally weighing 50 kg stands on a massless platform which oscillates up and down harmonically at a frequency of 2 s-1 and an amplitude 5 cm. A weighing machine on the platform gives the persons weight against time.
a) will there be any change in weight of the body, during the oscillation? b) if the answer to part a) is yes, what will be the maximum and minimum reading in the machine and at which position?...
Consider a pair of identical pendulums, which oscillate with equal amplitude independently such that when one pendulum is at its extreme position making an angle of 2o to the right with the vertical, the other pendulum makes an angle of 1o to the left of the vertical. What is the phase difference between the pendulums?
Answer: We can write the following set of equations: θ1 = θ0 sin (wt + δ1) ...............................(1) θ2 = θ0 sin (wt + δ2) ...
A mass of 2 kg is attached to the spring of spring constant 50 N/m. The block is pulled to a distance of 5 cm from its equilibrium position at x = 0 on a horizontal frictionless surface from rest at t = 0. Write the expression for its displacement at anytime t.
Answer: $ \omega =\sqrt{\frac{k}{m}}=5 $ Therefore, $ x=5\sin 5t $
A body of mass m is situated in a potential field U(x) = U0 (1 – cos αx) when U0 and α are constants. Find the time period of small oscillations.
Answer: According to the question, we have: U =U0 (1−cosαx) We know taht, F = −dU / dx $ F=-\frac{d}{dx}\left[ {{U}_{0}}(1-\cos \alpha x) \right] $ $ F=-{{U}_{0}}\alpha \sin \alpha x $ As it is...
Find the displacement of a simple harmonic oscillator at which its PE is half of the maximum energy of the oscillator.
Answer: we know that the mean position of the oscillator at x with PE is = 1/2 kx2 Therefore, PE = -m2x2 When PE is maximum, KE = 0 at x = A We get, E = 1/2 mω2A2 PE = 1/2 total energy x2 = 1/2 A2 x...
Show that the motion of a particle represented by y = sin ωt – cos ωt is simple harmonic with a period of 2π/ω.
Answer: A function that represents SHM is written as sin (2π/T t + ϕ) We have, y = sin ωt – cos ωt y = √2 sin (ωt – π/4) The standard equation of SHM has: y = a sin (2π/T t + ϕ) Therefore, T =...
Find the time period of mass M when displaced from its equilibrium position and then released for the system shown in the figure.
Answer: y represents the distance across which the mass is pulled. The spring's total extension is y + y = 2y. The initial mean location of equilibrium = x0 In the spring, the net extension is equal...
The length of a second’s pendulum on the surface of the earth is 1 m. What will be the length of a second’s pendulum on the moon?
Answer: We know that the expression for the time period of a simple pendulum is T = 2π√l/g Where l represents the length of the pendulum and, g denotes the acceleration due to gravity Therefore,...
Draw a graph to show the variation of PE, KE, and total energy of a simple harmonic oscillator with displacement.
Answer:
Show that for a particle executing SHM, velocity, and displacement have a phase difference of π/2.
Answer: We know that the equation for the displacement of SHM is x = a cos ꞷt where velocity can be determined as: v = dx/dt = -aꞷ sin ꞷt Here, the phase displacement is ϕ1 = ꞷt And the phase...
In figure, what will be the sign of the velocity of the point P’, which is the projection of the velocity of the reference particle P. P is moving in a circle of radius R in the anticlockwise direction.
Answer: P' is the perpendicular of the particle Pat's velocity vector at time t. When the particle moves from P to P1, its foot moves from P' to Q, which is away from the positive axis. As a result,...
What is the ratio between the distance travelled by the oscillator in one time period and amplitude?
Answer: According to the question, the distance traveled by the oscillator in one time period = 4A Where A represents the amplitude of the oscillation Therefore, the required ratio becomes = 4A/A =...
What is the ratio of maximum acceleration to the maximum velocity of a simple harmonic oscillator?
Answer: We know that the equation for the displacement of SHM is x = a sin (ꞷt + ϕ) And the velocity of the particle is given by- v = dx/dt = d a sin (ꞷt + ϕ)/dt Expression for the maximum velocity...
When will the motion of a simple pendulum be simple harmonic?
Answer: Consider a basic pendulum with a restoring torque and O as the fixed point. The restoring force is given as F = -mg sin θ θ is so small that θ = arc/radius = x/l As a result, F = – mg x/l As...
What are the two basic characteristics of a simple harmonic motion?
Answer: The two primary properties of a SHM are as follows: a) Acceleration and displacement are proportionate in magnitude. b) The acceleration is in the direction of the mean position, while the...
Two identical springs of spring constant K are attached to a block of mass m and to fixed supports as shown in the figure. When the mass is displaced from equilibrium position by a distance x towards the right, find the restoring force.
Answer: When mass m is pushed from equilibrium by a distance x to the right, spring B is squeezed by a distance x, and the force (kx) is applied to mass m to the left. However, spring A will stretch...
Displacement versus time curve for a particle executing SHM is shown. Identify the points marked at which
i) velocity of the oscillator is zero ii) speed of the oscillator is maximum Answer: (i) The oscillator's velocity is zero when the points A, C, E, and G are at their extreme positions. (ii) The...
A body is performing SHM. Then its
a) average total energy per cycle is equal to its maximum kinetic energy b) average kinetic energy per cycle is equal to half of its maximum kinetic energy c) mean velocity over a complete cycle is...
A particle is in linear simple harmonic motion between two points A and B, 10 cm apart. Taken the direction from A to B as the +ve direction and choose the correct statements.
a) the sign of velocity, acceleration, and force on the particle when it is 3 cm away from A going towards B are positive b) the sign of velocity of the particle at C going towards O is negative c)...
A body is performing SHM. Then its
a) average total energy per cycle is equal to its maximum kinetic energy b) average kinetic energy per cycle is equal to half of its maximum kinetic energy c) mean velocity over a complete cycle is...
The displacement time graph of a particle executing SHM is shown in the figure. Which of the following statement is/are true?
a) the force is zero at t = 3T/4 b) the acceleration is maximum at t = 4T/4 c) the velocity is maximum at t = T/4 d) the PE is equal to KE of oscillation t = T/2 Answer: The correct options are a)...
Which of the following statements is/are true for a simple harmonic oscillator?
a) force acting is directly proportional to the displacement from the mean position and opposite to it b) motion is periodic c) acceleration of the oscillator is constant d) the velocity is periodic...
Displacement versus time curve for a particle executing SHM is shown in the figure. Choose the correct statements.
a) phase of the oscillator is same at t = 0 s and t = 2 s b) phase of the oscillator is the same at t = 2 s and t = 6 s c) phase of the oscillator is the same at t = 1 s and t = 7 s d) phase of the...
The motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lower point is
a) simple harmonic motion b) non-periodic motion c) periodic motion d) periodic but not SHM Answer: The correct options are a) simple harmonic motion b) non-periodic motion Explanation: Allow the...
The rotation of the earth about its axis is
a) periodic motion b) simple harmonic motion c) periodic but not simple harmonic motion d) non-periodic motion Answer: The correct answers are a) periodic motion c) periodic but not simple harmonic...
When a mass m is connected individually to two springs S1 and S2, the oscillation frequencies are v1 and v2. If the same mass is attached to the two springs are shown in the figure, the oscillation frequency would be
a) v1 + v2 b) c) d) Answer: The correct option is b) Explanation: The spring constants for both the springs have been used in the expressions below: $ {{v}_{1}}=\frac{1}{2\pi...
A particle executing SHM has a maximum speed of 30 cm/s and a maximum acceleration of 60 cm/s2. The period of oscillation is
a) πs b) π/2 s c) 2 πs d) π/t s Answer: The correct option is a) πs Explanation: It isgiven that the maximum velocity is $ {{v}_{\max }}=A\omega =30cm/s $ And the maximum acceleration is as follows:...
Figure shows the circular motion of a particle. The radius of the circle, the period, sense of revolution, and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector of the rotating particle P is
a) x(t) = B sin (2πt/30) b) x(t) = B cos (πt/15) c) x(t) = B sin (πt/15 + π/2) d) x(t) = B cos (πt/15 + π/2) Answer: The correct option is a) x(t) = B sin (2πt/30) Explanation: We have, $ x(t)=A\sin...
Four pendulums A, B, C, and D are suspended from the same elastic support as shown in the figure. A and C are of the same length, while B is smaller than A and D is larger than A. If A is given a transverse displacement,
a) D will vibrate with maximum amplitude b) C will vibrate with maximum amplitude c) B will vibrate with maximum amplitude d) all four will oscillate with equal amplitude Answer: The correct option...
The displacement of a particle varies with time according to the relation y = a sin ωt + b cos ωt
a) the motion is oscillatory but not SHM b) the motion is SHM with amplitude a + b c) the motion is SHM with amplitude a2 + b2 d) the motion is SHM with amplitude √a2 + b2 Answer: The correct option...
A particle is acted simultaneously by mutually perpendicular simple harmonic motions x = a cos ωt and y = a sin ωt. The trajectory of motion of the particle will be
a) an ellipse b) a parabola c) a circle d) a straight line Answer: The correct option is c) a circle Given x=acosωt (i) y=asinωt ...
Motion of an oscillating liquid column in a U-tube is
a) periodic but not simple harmonic b) non-periodic c) simple harmonic and time period is independent of the density of the liquid d) simple harmonic and time period is directly proportional to the...
The relation between acceleration and displacement of four particles are given below:
a) ax = +2x b) ax = +2x2 c) ax = -2x2 d) ax = -2x Which one of the particles is executing simple harmonic motion? Answer: The correct option is d) ax = -2x Explanation: The acceleration in simple...
The displacement of a particle is represented by the equation y = sin3 ωt. The motion is
a) non-periodic b) periodic but not simple harmonic c) simple harmonic with period 2π/ω d) simple harmonic with period π/ω Answer: The correct option is c) simple harmonic with period 2π/ω The...
The displacement of a particle is represented by the equation y = 3 cos(π/4 – 2ωt). The motion of the particle is
a) simple harmonic with period 2p/w b) simple harmonic with period π/ω c) periodic but not simple harmonic d) non-periodic Answer: The correct option is b) simple harmonic with period π/ω...
Consider a rectangular block of wood moving with a velocity vo in a gas at temperature T and mass density ρ. Assume the velocity is along the x-axis and the area of cross-section of the block perpendicular to vo is A. Show that the drag force on the block is
, where m is the mass of the gas molecule. Answer: Let ρm represent the number of molecules per unit volume Then the expression for the change in momentum by a molecule on front side is = 2m (v +...
A box of 1.00 m3 is filled with nitrogen at 1.50 atm at 300 K. The box has a hole of an area 0.010 mm2. How much time is required for the pressure to reduce by 0.10 atm, if the pressure outside is 1 atm?
Answer: Volume of the box = 1 m3 = V1 Initial pressure P1 = 1.5 atm Final pressure P2 = 1.4 atm Air pressure Pa = 1 atm Initial temperature T1 = 300 K Final temperature T2 = 300 K Area of the hole =...
Ten small planners are flying at a speed of 150 km/h in total darkness in an air space that is 20 × 20 × 1.5 km3 in volume. You are in one of the planes, flying at random within this space with no way of knowing where the other planes are. On the average about how long a time will elapse between near collision with your plane. Assume for this rough computation that a safety region around the plane can be approximated by a sphere of radius 10 m.
Answer: We know that, Time = distance/speed Number of particles per unit volume v = N/volume n = 0.0167 km-3 d = 10 × 10-3 km v = 150 km/hr Therefore, we get: time = 225 hrs
Consider an ideal gas with the following distribution of speeds
Speed (m/s) % of molecules 200 10 400 20 600 40 800 20 1000 10 a) calculate Vrms and hence T (m = 3.0 × 10-26 kg) b) if all the molecules with speed 1000 m/s escape from the system, calculate new...
Explain why
a) there is no atmosphere on moon b) there is a fall in temperature with altitude Answer: a) The moon has no atmosphere since the gravitational pull is minimal and the Vrms is bigger on the moon,...
Answer: According to the question, the final KE of the gas is 0 The change in KE is as follows: ∆K= 1/2 (nm)v2 ∆T is the change in the temperature ∆U = nCv∆T ∆K = ∆U Making use of the expression, we...
Calculate the number of degrees of freedom of molecules of hydrogen in 1 cc of hydrogen gas at NTP.
Answer: According to the question, the volume occupied by the molecules of a gas is 22400 cc and the number of molecules in 1 cc of hydrogen are 2.688 × 1019 We know that the hydrogen has a total...
A balloon has 5.0 g mole of helium at 7 degrees C. Calculate
a) the number of atoms of helium in the balloon b) the total internal energy of the system Answer: We know that the average KE per molecule is 3/2kT No.of moles of helium are n = 5 g mole We have T...
When air is pumped into a cycle tyre the volume and pressure of the air in the tyre both are increased. What about Boyle’s law in this case?
Answer: We have, PV = P(m/ρ) = constant P/ ρ = constant Volume = m/ ρ where m is constant When air is pushed into the cycle's tyre, the mass of the air increases as the number of molecules...
We have 0.5 g of hydrogen gas in a cubic chamber of size 3 cm kept at NTP. The gas in the chamber is compressed keeping the temperature constant till a final pressure of 100 atm. Is one justified in assuming the ideal gas law, in the final state?
Answer: We know that volume of 1 molecule = 4/3 πr3 = 4.20 × 10-30 m3 And the number of moles in 0.5 g H2 gas = 0.25 mole Volume of H2 molecule in 0.25 mole = 1.04×6.023× 10+23-30 = 6.264 ×...
A gas mixture consists of molecules of tyres A, B, and C with masses mA > mB > mC. Rank the three types of molecules in decreasing order of
a) average KE b) rms speeds Answer: a) From the above result, the pressure and temperature are the same, therefore, KEc > KEb > KEa b) When P and T are constant, (Vrms)c > (Vrms)b >...
The container shown in the figure has two chambers, separated by a partition, of volumes V1 = 2.0 litre and V2 = 3.0 litre. The chambers contain μ1 = 4.0 and μ2 = 5.0 moles of a gas at pressure p1 = 1.00 atm and p2 = 2.00 atm. Calculate the pressure after the partition is removed and the mixture attains equilibrium.
V1 V2 μ1 μ2 p1 p2 Answer: We know that for an ideal gas, PV = μRT The two equations that we can write are: P1V1 = μ1R1T1 P2V2 = μ2R2T2 P1 = 1 atm, P2 = 2 atm and V1 = 2L, V2 = 3L Also, T1 = T = T2...
Calculate the ratio of the mean free paths of the molecules of two gases having molecular diameters 1 A and 2 A. The gases may be considered under identical conditions of temperature, pressure, and volume.
Answer: We know that that we can write: I α (1/d2) d1 = 1Å d2 = 2Å Therefore, l1 : l2 = 4 : 1 The ratio of the mean free paths of the molecules is 4:1
A gas mixture consists of 2.0 moles of oxygen and 4.0 moles of neon a temperature T. Neglecting all vibrational modes, calculate the total internal energy of the system. (Oxygen has two rotational modes.)
Answer: We know that oxygen has 5 degrees of freedom. Therefore, energy per mole = (5/2)RT Therefore, for 2 moles of oxygen, energy = 5RT Neon has 3 degrees of freedom. Therefore, energy per mole...
Two molecules of a gas have speeds of 9 × 106 m/s and 1 × 106 m/s respectively. What is the root mean square speed of these molecules?
Answer: Expression for root mean square velocity is as follows: $ {{v}_{rms}}=\sqrt{\frac{v_{1}^{2}+v_{2}^{2}+v_{3}^{2}+......+v_{n}^{2}}{n}} $ For two meolecules, the formula reduces to: $...
The molecules of a given mass of a gas have root mean square speeds of 100 m/s at 27oC and 1.00 atmospheric pressure. What will be the root mean square speeds of the molecules of the gas at 127oC and 2.0 atmospheric pressure?
Answer: According to the question, Vrms = 100 m/s T1 = 300 K and T2 = 400 K Expression for root mean square velocity is Vrms = √3RT/M Upon substituting the given values, we get Vrms = 115.4...
The volume of a given mass of a gas at 27 degrees C, 1 atm is 100 cc. What will be its volume at 327oC?
Answer: According to the question, T1 = 27oC = 300 K and the volume V1 = 100 cm3 It is known that V is proportional to T So, we can write V/T = constant Or, V1/T1 = V2/T2 Upon re-arranging, we have...
Calculate the number of atoms in 39.4 g gold. Molar mass of gold is 197 g/mole.
Answer: According to the question, the molar mass = mass of Avagadro's number of atoms = 6.023 × 1023 atoms Mass of gold is m = 39.4 g and the molar mass of gold is M = 197 g/mol We know that 197 g...
When an ideal gas is compressed adiabatically, its temperature rises: the molecules on the average have more kinetic energy than before. The kinetic energy increases,
a) because of collisions with moving parts of the wall only b) because of collisions with the entire wall c) because the molecules gets accelerated in their motion inside the volume d) because of...
Which of the following diagrams depicts ideal gas behaviour?
Answer: The correct answer is a) c)
In a diatomic molecules, the rotational energy at a given temperature
a) obeys Maxwell’s distribution b) have the same value for all molecules c) equals the translational kinetic energy for each molecule d) is 2/3rd the translational kinetic energy for each molecule...
Diatomic molecules like hydrogen have energies due to both translational as well as rotational motion. From the equation in kinetic theory pV = 2/3 E, E is
a) the total energy per unit volume d) only the translational part of energy because rotational energy is very small compared to the translational energy c) only the translational part of the energy...
ABCDEFGH is a hollow cube made of an insulator. Face ABCD has a positive charge on it. Inside the cube, we have ionized hydrogen. The usual kinetic theory expression for pressure
a) will be valid b) will not be valid since the ions would experience forces other than due to collision with the walls c) will not be valid since collisions with walls would not be elastic d) will...
An inflated rubber balloon contains one mole of an ideal gas, has a pressure p, volume V, and temperature T. If the temperature rises to 1.1T and the volume is increased to 1.05V, the final pressure will be
a) 1.1 p b) p c) less than p d) between p and 1.1 Answer: The correct option is d) between p and 1.1 Explanation:
A vessel of volume V contains a mixture of 1 mole of hydrogen and 1 mole of oxygen. Let f1(v)dv, denote the fraction of molecules with speed between v and (v + dv) with f2(v)dv similarly for oxygen. Then
a) f1(v) + f2(v) = f(v) obeys the Maxwell’s distribution law b) f1(v), f2(v) will obey the Maxwell’s distribution law separately c) neither f1(v) nor f2(v) will obey the Maxwell’s distribution law...
1 mole of H2 gas is contained in a box of volume V = 1.00 m3 at T = 300 K. The gas is heated to a temperature of T = 3000 K and the gas gets converted to a gas of hydrogen atoms. The final pressure would be
a) same as the pressure initially b) 2 times the pressure initially c) 10 times the pressure initially d) 20 times the pressure initially Answer: The correct option is d) 20 times the pressure...
Volume versus temperature graphs for a given mass of an ideal gas are shown in the figure at two different values of constant pressure. What can be inferred about the relation between P1 and P2?
a) P1 > P2 b) P1 = P2 c) P1 < P2 d) data is insufficient Answer: The correct option is a) P1 > P2 Explanation: When the pressure of an ideal gas is constant, Chale's law is obeyed, i.e. V ∝...
A cylinder containing an ideal gas is in a vertical position and has a piston of mass M that is able to move up or down without friction. If the temperature is increased,
a) both p and V of the gas will change b) only p will increase according to Charle’s law c) V will change but not p d) p will change but not V Answer: The correct option is c) V will change but not...
Boyle’s law is applicable for an
a) adiabatic process b) isothermal process c) isobaric process d) isochoric process Answer: The correct option is b) isothermal process Explanation: In an isothermal process, when the temperature...
1 mole of an ideal gas is contained in a cubical volume V, ABCDEFGH at 300 K. One face of the cube (EFGH) is made up of a material which totally absorbs any gas molecule incident on it. At any given time,
a) the pressure on EFGH would be zero b) the pressure on all the faces will the equal c) the pressure of EFGH would be double the pressure on ABCD d) the pressure on EFGH would be half that on ABCD...
A cubic vessel (with faces horizontal + vertical) contains an ideal gas at NTP. The vessel is being carried by a rocket which is moving at a speed of 500 m/s in the vertical direction. The pressure of the gas inside the vessel as observed by us on the ground
a) remains the same because 500 m/s is very much smaller than vrms of the gas b) remains the same because the motion of the vessel as a whole does not affect the relative motion of the gas molecules...
Consider one mole of a perfect gas in a cylinder of unit cross-section with a piston attached. A spring is attached to the piston and to the bottom of the cylinder. Initially the spring is unstretched and the gas is in equilibrium. A certain amount of heat Q is supplied to the gas causing an increase of volume from V0 to V1.
c) using the first law of thermodynamics, write down the relation between Q, Pa, V, V0, and k. Answer: c) The relation between Q, Pa, V, V0, and k is as follows: dQ = dU + dW where, dU = Cv (T – T0)...
Consider one mole of a perfect gas in a cylinder of unit cross-section with a piston attached. A spring is attached to the piston and to the bottom of the cylinder. Initially the spring is unstretched and the gas is in equilibrium. A certain amount of heat Q is supplied to the gas causing an increase of volume from V0 to V1.
a) what is the initial pressure of the system? b) what is the final pressure of the system? Answer: a) Pa is the initial pressure of the system inside the cylinder b) The final pressure of the...
Consider that an ideal gas is expanding in a process given by P = f(V), which passes through a point (V0, P0). Show that the gas is absorbing heat at (P0, V0) if the slope of the curve P = f(V) is larger than the slope of the adiabat passing through (P0, V0).
Answer: The slope of the graph as given by: $ \left( {{V}_{0}},{{P}_{0}} \right)={{\left( \frac{dP}{dV} \right)}_{{{V}_{0}},{{P}_{0}}}} $ Making use of the above relation, we can determine that $...
A cycle followed by an engine is shown in the figure. Find heat exchanged by the engine, with the surroundings for each section of the cycle considering Cv = (3/2)R.
AB: constant volume BC: constant pressure CD: adiabatic DA: constant pressure Answer: a) AB: constant volume b) BC: constant pressure c) CD: adiabatic QCD = 0 d) DA: constant pressure, there is...
A cycle followed by an engine is shown in the figure.
A to B: volume constant B to C: adiabatic C to D: volume constant D to A: adiabatic VC = VD = 2VA = 2VB c) what is the work done by the engine in one cycle in terms of PA, PB, VA? d) what is the...
A cycle followed by an engine is shown in the figure.
A to B: volume constant B to C: adiabatic C to D: volume constant D to A: adiabatic VC = VD = 2VA = 2VB a) in which part of the cycle heat is supplied to the engine from outside? b) in which part of...
Consider a P-V diagram in which the path followed by one mole of a perfect gas in a cylindrical container is shown in the figure.
c) given the internal energy for one mole of gas at temperature T is (3/2)RT, find the heat supplied to the gas when it is taken from state 1 to 2 with V2 = 2V1. Answer: We know that the expression...
Consider a P-V diagram in which the path followed by one mole of a perfect gas in a cylindrical container is shown in the figure.
a) find the work done when the gas is taken from state 1 to state 2 b) what is the ratio of temperature T1/T2 if V2 = 2V1 Answer: According to the question, PV1/2 = K = constant a) Expression for...
A person driving a car suddenly applies the brakes on seeing a child on the road ahead. If he is not wearing a seat belt, he falls forward and hits his head against the steering wheel. Why?
If a person is not wearing a seat belt and abruptly hits the brakes, he will fall forward and bang his head against the steering wheel because his upper body will continue to move in the same...
The position time graph of a body of mass 2 kg is as given in the figure. What is the impulse on the body at t – 0 sec and t = 4 sec.
Mass of body, m = 2 kg Time, t = 0 Initial velocity, v1 = 0 From graph, we know that t ≥ 0 to t ≤ 4 which is a straight line. The velocity of the body is constant v2 = tan θ = 3/4 = 0.75 m/s At t ≥...
A person of mass 50 kg stands on a weighing scale on a lift. If the lift is descending with a downward acceleration of 9 m/s2 what would be the reading of the weighing scale?
When the lift lowers with an acceleration a, the apparent weight on the weighing scale decreases. W' denotes the apparent weight. Therefore, W' = R = (mg – ma) = m(g – a) As a result, W' = 50(10-9)...
A girl riding a bicycle along a straight road with a speed of 5 m/s throws a stone of mass 0.5 kg which has a speed of 15 m/s with respect to the ground along her direction of motion. The mass of the girl and the bicycle is 50 kg. Does the speed of the bicycle change after the stone is thrown? What is the change in speed, if so?
Given, m1 = 50 kg m2 = 0.5 kg u1 = 5 m/s u2 = 5 m/s v1 = ? v2 = 15 m/s The law of conservation of momentum states that Final momentum equals initial momentum. u1 = m1v1 + m2v2 (m1 + m2) We obtain by...
Two billiard balls A and B, each of mass 50 g and moving in opposite directions with speed of 5 m/s each, collide and rebound with the same speed. If the collision lasts for 10-3 seconds, which of the following statements are true? a) the impulse imparted to each ball is 0.25 kg.m/s and the force on each ball is 250N b) the impulse imparted to each ball is 0.25 kg.m/s and the force exerted on each ball is 25 × 10-5 N c) the impulse imparted to each ball is 0.5 Ns d) the impulse and the force on each ball are equal in magnitude and opposite in direction
The correct answer is: c) the impulse imparted to each ball is 0.5 Ns d) the impulse and the force on each ball are equal in magnitude and opposite in direction
In the figure, a body A of mass m slides on a plane inclined at angle θ1 to the horizontal and μ1 is the coefficient of friction between A and the plane. A is connected by a light string passing over a frictionless pulley to another body B, also of mass m, sliding on a frictionless plane inclined at angle θ2 to the horizontal. Which of the following statements are true?;a) A will never move up the plane b) A will just start moving up the plane when 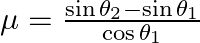 c) for A to move up the plane, θ2 must always be greater than θ1 d) B will always slide down with constant speed
c) for A to move up the plane, θ2 must always be greater than θ1 d) B will always slide down with constant speed
The correct answer is: b) A will just start moving up the plane when \(\mu =\frac{\sin {{\theta }_{2}}-\sin {{\theta }_{1}}}{\cos {{\theta }_{1}}}\) c) for A to move up the plane, θ2 must always be...
Mass m1 moves on a slope making an angle θ with the horizontal and is attached to mass m2 by a string passing over a frictionless pulley as shown in the figure. The coefficient of friction between m1 and the sloping surface is μ. Which of the following statements are true?;a) if m2 > m1 sin θ, the body will move up the plane b) if m2 > m1(sin θ + μ cos θ), the body will move up the plane c) if m2 < m1 (sin θ + μ cos θ), the body will move up the plane d) if m2 < m1 (sin θ – μ cos θ), the body will move down the plane
The correct answer is: b) if m2 > m1(sin θ + μ cos θ), the body will move up the plane d) if m2 < m1 (sin θ – μ cos θ), the body will move down the plane
In figure, the coefficient of friction between the floor and the body B is 0.1. The coefficient of friction between the bodies B and A is 0.2. A force F is applied as shown on B. The mass of A is m/2 and of B is m. Which of the following statements are true?;a) the bodies will move together if F = 0.25 mg b) the body A will slip with respect to B if F = 0.5 mg c) the bodies will move together if F = 0.5 mg d) the bodies will be at rest if F = 0.1 mg e) the maximum value of F for which the two bodies will move together is 0.45 mg
The correct answer is: a) the bodies will move together if F = 0.25 mg b) the body A will slip with respect to B if F = 0.5 mg d) the bodies will be at rest if F = 0.1 mg e) the maximum value of F...
The motion of a particle of mass m is given by x = 0 for t < 0 sec, x(t) = A sin 4p t for 0 < t < (1/4) sec, and x = 0 for t > (1/4) sec. Which of the following statements is true? a) the force at t = (1/8) sec on the particle is -16π2Am b) the particle is acted upon by on impulse of magnitude 4π2Am at t = 0 sec and t = (1/4) sec c) the particle is not acted upon by any force d) the particle is not acted upon by a constant force e) there is no impulse acting on the particle
The correct answer is: a) the force at t = (1/8) sec on the particle is -16π2Am b) the particle is acted upon by on impulse of magnitude 4π2Am at t = 0 sec and t = (1/4) sec d) the particle is not...
A car of mass m starts from rest and acquires a velocity along the east a in two seconds. Assuming the car moves with uniform acceleration, the force exerted on the car is a) mv/2 eastward and is exerted by the car engine b) mv/2 eastward and is due to the friction on the tyres exerted by the road c) more than mv/2 eastward exerted due to the engine and overcomes the friction of the road d) mv/2 exerted by the engine
The correct answer is b) mv/2 eastward and is due to the friction on the tyres exerted by the road
A body with mass 5 kg is acted upon by a force F=-3i+4j N. If its initial velocity at t = 0 is v=6i-12j m/s, the time at which it will just have a velocity along the y-axis is a) never b) 10 s c) 2 s d) 15 s
The correct answer is b) 10 s
A body of mass 2 kg travels according to the law x(t) = p(t) + qt2 + rt3 where p = 3 m/s, q = 4 m/s2, and r = 5 m/s3. The force acting on the body at t=2 seconds is a) 136 N b) 134 N c) 158 N d) 68 N
The correct answer is a) 136 N
Conservation of momentum in a collision between particles can be understood from a) conservation of energy b) Newton’s first law only c) Newton’s second law only d) both Newton’s second and third law
The correct answer is d) both Newton’s second and third law
In the previous problem, the magnitude of the momentum transferred during the hit is a) zero b) 0.75 kg.m/s c) 1.5 kg.m/s d) 14 kg.m/s
The correct option is c) 1.5 kg.m/s
A cricket ball of mass 150 g has an initial velocity u=3i+4j m/s and a final velocity v=-(3i+4j) m/s after being hit. The change in momentum a) zero (b)-(0.45i+0.6j) (c)-(0.9i+1.2j)) (d)-5(i+j)
The correct answer is (c) -(0.9i+1.2j)
A metre scale is moving with uniform velocity. This implied a) the force acting on the scale is zero, but a torque about the centre of mass can act on the scale b) the force acting on the scale is zero and the torque acting about the centre of mass of the scale is also zero c) the total force acting on it need not be zero but the torque on it is zero d) neither the force nor the torque needs to be zero
The correct answer is b) the force acting on the scale is zero and the torque acting about the centre of mass of the scale is also zero
A ball is travelling with uniform translator motion. This means that a) it is at rest b) the path can be a straight line or circular and the ball travels with uniform speed c) all parts of the ball have the same velocity and the velocity is constant d) the centre of the ball moves with constant velocity and the ball spins about its centre uniformly
The correct option is c) all parts of the ball have the same velocity and the velocity is constant
A balloon filled with helium rises against gravity increasing its potential energy. The speed of the balloon also increases as it rises. How do you reconcile this with the law of conservation of mechanical energy? You can neglect the viscous drag of air and assume that the density of air is constant.
The net buoyant force Equals vpg when the dragging viscous force of the air on the balloon is ignored. Where v is the volume of air that has been displaced. The upward net density is denoted by p....
Two identical steel cubes collide head-on face to face with a speed of 10 cm/s each. Find the maximum compression of each. Young’s modulus for steel = Y = 2 × 1011 N/m2.
Y = stress/strain Y = FL/A∆L WD = F∆L KE = 5 × 10-4 J WD = KE ∆L = 5 × 10-7 m
A rocket accelerates straight up by ejecting gas downwards. In a small time interval ∆t, it ejects a gas of mass ∆m at a relative speed u. Calculate KE of the entire system at t + ∆t and t and show that the device that ejects gas does work = (1/2) ∆m u2 in this time interval.
M is the rocket's mass at any given moment t. The rocket's velocity is v. The mass of the gas expelled during the time interval t is m. As a result, K = 1/2 u2∆m
A curved surface as shown in the figure. The portion BCD is free of friction. There are three spherical balls of identical radii and masses. Balls are released from one by one from A which is at a slightly greater height than C. with the surface AB, ball 1 has large enough friction to cause rolling down without slipping; ball 2 has a small friction and ball 3 has a negligible friction. a) for which balls is total mechanical energy conserved? b) which ball can reach D? c) for balls which do not reach D, which of the balls can reach back A?
a) For ball 1 the total mechanical energy is conserved b) Ball 1 reaches D c) Ball 3 reaches back A
A block of mass 1 kg is pushed up a surface inclined to horizontal at an angle of 30o by a force of 10 N parallel to the inclined surface. The coefficient of friction between the block and the incline is 0.1. If the block is pushed up by 10 m along the incline, calculate a) work done against gravity b) work done against the force of friction c) increase in potential energy d) increase in kinetic energy e) work done by an applied force
a) Work against gravity equals mgh 5 m= h 50 J WD against gravity b) The work done against the friction force is fs = 53 J. d) WD against gravity = 50 J increase in PE d) The system's increase in KE...
On complete combustion, a litre of petrol gives off heat equivalent to 3 × 107 J. In a test drive a car weighing 1200 kg, including the mass of driver, runs 15 km per litre while moving with a uniform speed on a surface and air to be uniform, calculate the force of friction acting on the car during the test drive, if the efficiency of the car engine were 0.5.
car engine Efficiency = 0.5 Energy given by the car with 1 litre of petrol = 1.5 × 107 WD = 1.5 × 107 f = 103 N
An adult weighing 600 N raises the centre of gravity of his body by 0.25 m while taking each step of 1 m length in jogging. If he jogs for 6 km, calculate the energy utilized by him in jogging assuming that there is no energy loss due to friction of ground and air. Assuming that the body of the adult is capable of converting 10% of energy intake in the form of food, calculate the energy equivalents of food that would be required to compensate energy utilized for jogging.
The energy used up is given as = mgh mg = 600 N h = 0.25m No.of steps in 6 km = 6000 steps Energy used in 6000 m = (6000)(600)(0.25)J Energy utilized in jogging = 9 × 104 J
An engine is attached to a wagon through a shock absorber of length 1.5 m. The system with a total mass of 50,000 kg is moving with a speed of 36 km/h when the brakes are applied to bring it to rest. In the process of the system being brought to rest, the spring of the shock absorber gets compressed by 1.0 m. If 90% of the energy of the wagon is lost due to friction, calculate the spring constant.
KE = 1/2 mv2 m = 50000 kg v = 10 m/s KE = 2500000J KE of spring = 10% of the KE wagon K = 5 × 105 N/m
Suppose the average mass of raindrops is 3.0 × 10^(-5) kg and their average terminal velocity 9 m/s. Calculate the energy transferred by rain to each square meter of the surface at a place which receives 100 cm of rain in a year.
Energy transferred by the rain to the surface of the earth = 1/2 mv2 The velocity of the rain = 9 m/s Mass = (volume)(density) = 1000 kg Energy transferred by 100 cm rainfall = 1/2 mv2 =...
Two pendulums with identical bobs and lengths are suspended from a common support such that in rest position the two bobs are in common. One of the bobs is released after being displaced by 10o so that it collides elastically head-on with the other bob. a) describe the motion of two bobs b) draw a graph showing variation in energy of either pendulum with time for 0 ≤ t ≤ 2T where T is the period of each pendulum
A raindrop of mass 1.00 g falling from a height of 1 km hits the ground with a speed of 50 m/s. Calculate a) the loss of PE of the drop b) the gain in KE of the drop c) is the gain in KE equal to loss of PE? If not why?
a) PE at the highest point = 10 J b) Gain in KE = 1/2 mv2 = 1.250 J c) Gain in KE is not equal to the PE
The bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in the figure. If the length of the pendulum is 1 m, calculate a) the height to which bob A will rise after collision b) the speed with which bob B starts moving. Neglect the size of the bobs and assume the collision to be elastic.
a) After the impact, bob A does not rise much because the PE of bob A is converted to KE and the momentum is transferred to bob B. (B) The speed of bob B is calculated as the sum of bob A's KE and...
Consider a one-dimensional motion of a particle with total energy E. There are four regions A, B, C, and D in which the relation between potential energy V, kinetic energy (K) and total energy is as given below: Region A: V > E Region B: V < E Region C: K > E Region D: V > K State with reason in each case whether a particle can be found in the given region or not.
E = V + K and V > E for area A, implying that the KE is negative and therefore this is not feasible. K = E – V and V E for area B, implying that both energies are larger than zero. V = E – K and...
A ball of mass m, moving with a speed 2v0 collides inelastically with an identical ball at rest. Show that a) for a head-on collision, both the balls move forward b) for a general collision, the angle between the two velocities of scattered balls is less than 90o.
a) Let v1 and v2 be the velocities of the two balls after the collision. According to the law of conservation of momentum, mv0 = mv1 + mv2 v2 = v1 + 2ev0 e < 1 b) Using the law of conservation of...
A graph of potential energy V(x) versus x is shown in the figure. A particle of energy E0 is executing motion in it. Draw graph of velocity and kinetic energy versus x for one complete cycle AFA.
From the given graph of KE versus x From the below graph of velocity versus x
A bob of mass m suspended by a light string of length L is whirled into a vertical circle as shown in the figure. What will be the trajectory of the particle if the string is cut at a) point B b) point C c) point X
a) When the string is severed at point B, the particle's tangential velocity will be vertically downward, and the bob will travel in the same direction. b) When the string is severed at point C, the...
Two bodies of unequal mass are moving in the same direction with equal kinetic energy. The two bodies are brought to rest by applying retarding force of the same magnitude. How would the distance moved by them before coming to rest compare?
KE1 = KE2 WD1 = WD2 F1s1 = F2s2 F1 = F2 s1 = s2
Give an example of a situation in which an applied force does not result in a change in kinetic energy.
The kinetic energy of work done in a circular motion remains unchanged.
The average work done by a human heart while it beats once is 0.5 J. Calculate the power used by heart if it beats 72 times in a minute.
P = WD/time WD is one beat of heart = 0.5 J WD in 72 beats = 36 J P = WD/t = 0.6 W
Calculate the power of a crane in watts, which lifts a mass of 100 kg to a height of 10 min 20 sec.
P = WD/time = Fs cos θ/t = mgh cos θ/t h = 10 m t = 20 sec F = mg = 1000 Therefore, P = 500 Watts
In an elastic collision of two billiard balls, which of the following quantities remain conserved during the short time of collision of the balls a) kinetic energy b) total linear momentum Give a reason for your answer in each case.
Because there is no non-conservative force, the kinetic energy and total linear momentum of the billiard balls are preserved.
A body is moved along a closed loop. Is the work done in moving the body necessarily zero? If not, state the condition under which work done over a closed path is always zero.
When the conservative force acts on the body during motion, the work done by the moving body is zero. When a non-conservative force acts on a moving body, the work done by the body is not zero.
A body falls towards earth in the air. Will its total mechanical energy be conserved during the fall? Justify.
The free-falling body's total mechanical energy is not preserved since it is utilised to overcome the frictional force of the air molecules.
Calculate the work done by a car against gravity in moving along a straight horizontal road. The mass of the car is 400 kg and the distance moved is 2m.
WD = Fs cos θ WD = Fs cos 90o = 0 Hence, the work done by the car against the gravity is zero.
A body is being raised to a height h from the surface of the earth. What is the sign of work done by a) applied force b) gravitational force
a) The applied force produces positive work. b) The gravitational pull produces negative work.
Why is electrical power required at all when the elevator is descending? Why should there be a limit on the number of passengers in this case?
In the event of an elevator falling, the number of passengers is limited because it is not a free fall and descends at a constant speed.
A rough inclined plane is placed on a cart moving with a constant velocity u on horizontal ground. A block of mass M rests on the incline. Is any work done by a force of friction between the block and incline? Is there then a dissipation of energy?
The block is clearly tilted on the plane in the illustration above. There is no work done since there is no displacement and no waste of energy.
Two blocks M1 and M2 having equal mass are free to move on a horizontal frictionless surface. M2 is attached to a massless spring as shown in the figure. Initially, M2 is at rest and M1 is moving toward M2 with speed v and collides head-on with M2.;a) while spring is fully compressed all the KE of M1 is stored as PE of spring b) while spring is fully compressed the system momentum is not conserved, though final momentum is equal to the initial momentum c) if spring is massless, the final state of the M1 is the state of rest d) if the surface on which blocks are moving has friction, then a collision cannot be elastic
c) if spring is massless, the final state of the M1 is a state of rest d) if the surface on which blocks are moving has friction, then a collision cannot be elastic
A bullet of mass m fired at 30o to the horizontal leaves the barrel of the gun with a velocity v. The bullet hits a soft target at a height h above the ground while it is moving downward and emerges out with half the kinetic energy it had before hitting the target. Which of the following statements are correct in respect of bullet after it emerges out of the target? a) the velocity of the bullet will be reduced to half its initial value b) the velocity of the bullet will be more than half of its earlier velocity c) the bullet will continue to move along the same parabolic path d) the bullet will move in a different parabolic path e) the bullet will fall vertically downward after hitting the target f) the internal energy of the particles of the target will increase
b) the velocity of the bullet will be more than half of its earlier velocity d) the bullet will move in a different parabolic path f) the internal energy of the particles of the target will...
A man, of mass m, standing at the bottom of the staircase, of height L, climbs it and stands at its top. a) work done by all forces on man is zero b) work done by all the force on man is zero c) work done by the gravitational force on man is mgL d) the reaction force from a step does not do work because the point of application of the force does not move while the force exists
b) work done by all the force on man is zero d) the reaction force from a step does not do work because the point of application of the force does not move while the force exists
A cricket ball of mass 150 g moving with a speed of 126 km/h hits at the middle of the bat, held firmly at its position by the batsman. The ball moves straight back to the bowler after hitting the bat. Assuming that collision between ball and bat is completely elastic and the two remain in contact for 0.001 sec, the force that the batsman had to apply to hold the bat firmly at its place would be a) 10.5 N b) 21 N c) 1.05 × 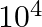 N d)
N d)  N
N
c) 1.05 × 104 N
Which of the diagrams in figure correctly shows the change in kinetic energy of an iron sphere falling freely in a lake having sufficient depth to impart it a terminal velocity?
(b
