Solution: Option(C) To find: Area of $A B C$ Given: $A(3,-2), B(k, 2)$ and $C(8,8)$ The formula used: $\Delta=\frac{1}{2}\left|\begin{array}{lll}x_{1} & y_{1} & 1 \\ x_{2} & y_{2} &...
Mark the tick against the correct answer in the following: If the points
Mark the tick against the correct answer in the following: The vertices of a a 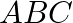 are
are 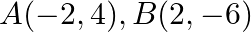 and
and  The area of a
The area of a  is
is
A. 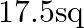 units
units
B. 35 sq units
C. 32 sq units
D. 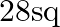 units
units
Solution: Option(B) To find: Area of $A B C$ Given: $A(-2,4), B(2,-6)$ and $C(5,4)$ Formula used: $\Delta=\frac{1}{2}\left|\begin{array}{lll}x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1 \\...
Mark the tick against the correct answer in the following: The solution set of the equation 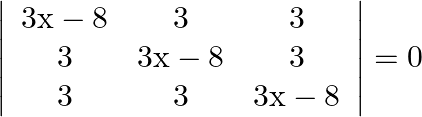 is
is
A. 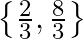
B. 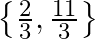
C. 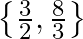
D. None of these
Solution: Option(B) To find: Value of $x$ We have, $\left|\begin{array}{ccc}3 x-8 & 3 & 3 \\ 3 & 3 x-8 & 3 \\ 3 & 3 & 3 x-8\end{array}\right|=0$ Applying $\mathrm{R}_{1}...
Mark the tick against the correct answer in the following: The solution set of the equation 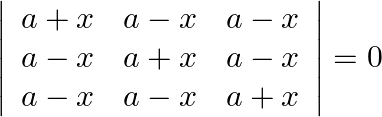 is
is
A. 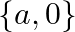
B. 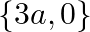
C. 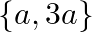
D. None of these
Solution: Option(B) To find: Value of $x$ We have, $\left|\begin{array}{ccc}a+x & a-x & a-x \\ a-x & a+x & a-x \\ a-x & a-x & a+x\end{array}\right|=0$ Applying...
Mark the tick against the correct answer in the following: The solution set of the equation 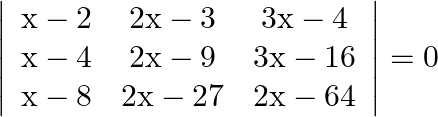 is
is
A. 
B. 
C. 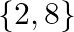
D. 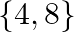
Solution: Option(A) To find: Value of $x$ We have, $\left|\begin{array}{ccc}x-2 & 2 x-3 & 3 x-4 \\ x-4 & 2 x-9 & 3 x-16 \\ x-8 & 2 x-27 & 3 x-64\end{array}\right|=0$ Applying...
Mark the tick against the correct answer in the following: The solution set of the equation 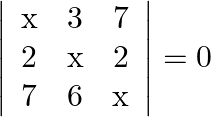 is
is
A. 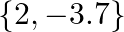
B. 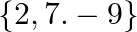
C. 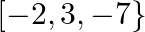
D. none of these
Solution: Option(C) To find: Value of $x$ We have, $\left|\begin{array}{lll}\mathrm{x} & 3 & 7 \\ 2 & \mathrm{X} & 2 \\ 7 & 6 & \mathrm{x}\end{array}\right|=0$ Applying...
Mark the tick against the correct answer in the following: If 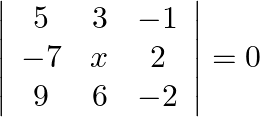 then
then 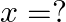
A. 0
B. 6
C. 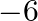
D. 9
Solution: Option(C) To find: Value of $\mathrm{x}$ We have, $\left|\begin{array}{ccc}5 & 3 & -1 \\ -7 & x & 2 \\ 9 & 6 & -2\end{array}\right|=0$ Applying $R_{1} \rightarrow 2...
Mark the tick against the correct answer in the following: 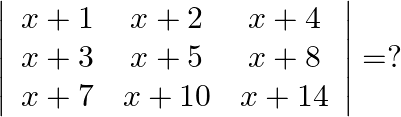
A. 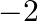
B. 2
C. 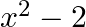
D. 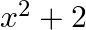
Solution: Option(A) To find: Value of $\left|\begin{array}{ccc}\mathrm{x}+1 & \mathrm{x}+2 & \mathrm{x}+4 \\ \mathrm{x}+3 & \mathrm{x}+5 & \mathrm{x}+8 \\ \mathrm{x}+7 &...
Mark the tick against the correct answer in the following: 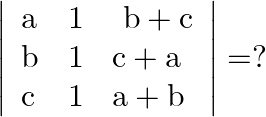
A. 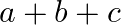
B. 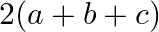
C. 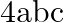
D. 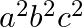
Solution: Option(C) To find: Value of $\left|\begin{array}{lll}a & 1 & b+c \\ b & 1 & c+a \\ c & 1 & a+b\end{array}\right|$ We have, $\left|\begin{array}{lll}a & 1 &...
Mark the tick against the correct answer in the following: 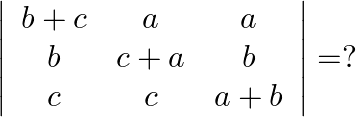
A. 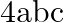
B. 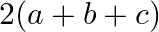
C. 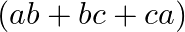
D. none of these
Solution: Option(A) To find: Value of $\left|\begin{array}{ccc}b+c & a & a \\ b & c+a & b \\ c & c & a+b\end{array}\right|$ We have, $\left|\begin{array}{ccc}b+c & a...
Mark the tick against the correct answer in the following: 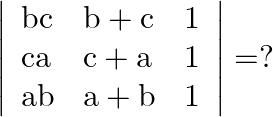
A. 
B. 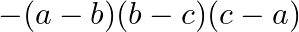
C. 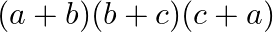
D. None of these
Solution: Option(A) To find: Value of $\left|\begin{array}{lll}\mathrm{bc} & \mathrm{b}+\mathrm{c} & 1 \\ \mathrm{ca} & \mathrm{a}+\mathrm{c} & 1 \\ \mathrm{ab} &...
Mark the tick against the correct answer in the following: 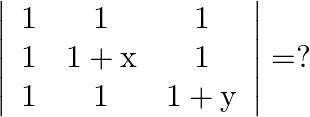
A. 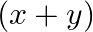
B. 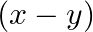
C. 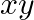
D. none of these
Solution: Option(C) To find: Value of $\left|\begin{array}{ccc}1 & 1 & 1 \\ 1 & 1+x & 1 \\ 1 & 1 & 1+y\end{array}\right|$ We have, $\left|\begin{array}{ccc}1 & 1 & 1...
Mark the tick against the correct answer in the following: 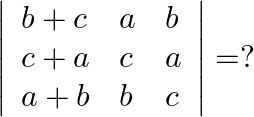
A. 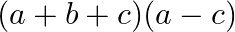
B. 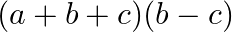
C. 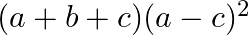
D. 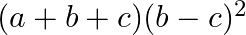
Solution: Option(C) To find: Value of $\left|\begin{array}{lll}b+c & a & b \\ c+a & c & a \\ a+b & b & c\end{array}\right|$ We have,...
Mark the tick against the correct answer in the following: 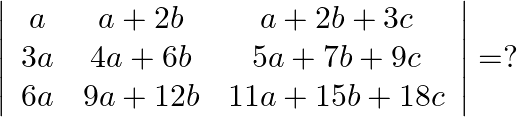
A. 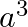
B. 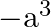
C. 0
D. none of these
Solution: Option(B) To find: Value of $\left|\begin{array}{ccc}a & a+2 b & a+2 b+3 c \\ 3 a & 4 a+6 b & 5 a+7 b+9 c \\ 6 a & 9 a+12 b & 11 a+15 b+18 c\end{array}\right|$ We...
Mark the tick against the correct answer in the following: 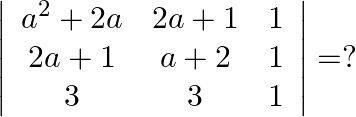
A. 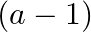
B. 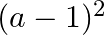
C. 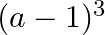
D. none of these
Solution: Option(C) To find: Value of $\left|\begin{array}{ccc}a^{2}+2 a & 2 a+1 & 1 \\ 2 a+1 & a+2 & 1 \\ 3 & 3 & 1\end{array}\right|$ We have,...
Mark the tick against the correct answer in the following: 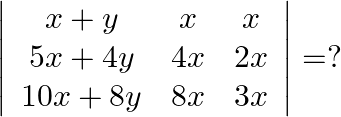
A. 0
B. 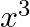
C. 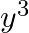
D. none of these
Solution: Option( B) To find: Value of $\left|\begin{array}{ccc}x+y & x & x \\ 5 x+4 y & 4 x & 2 x \\ 10 x+8 y & 8 x & 3 x\end{array}\right|$ We have,...
Mark the tick against the correct answer in the following: If 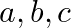 be distinct positive real numbers then the value of
be distinct positive real numbers then the value of 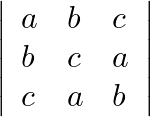 is
is
A. positive
B. negative
C. a perfect square
D. 0
Solution: Option(B) To find: Nature of $\left|\begin{array}{lll}a & b & c \\ b & c & a \\ c & a & b\end{array}\right|$ We have, $\left|\begin{array}{lll}a & b & c \\...
Mark the tick against the correct answer in the following: 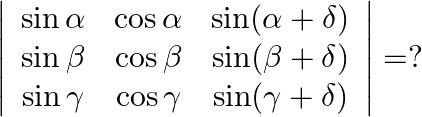
A. 0
B. 1
C. 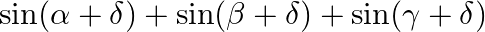
D. none of these
Solution: Option(A) To find: Value of $\left|\begin{array}{lll}\operatorname{sind} & \cos \alpha & \sin (\alpha+\bar{\delta}) \\ \sin \beta & \cos \beta & \sin (\beta+\bar{\delta})...
Mark the tick against the correct answer in the following: 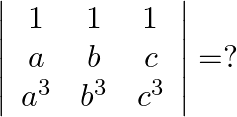
A. 
B. 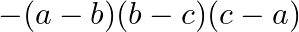
C. 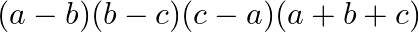
D. 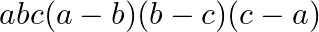
Solution: Option(C) To find: Value of $\left|\begin{array}{ccc}1 & 1 & 1 \\ a & b & c \\ a^{3} & b^{3} & c^{3}\end{array}\right|$ We have, $\left|\begin{array}{ccc}1 & 1...
Mark the tick against the correct answer in the following: 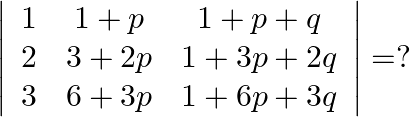
A. 0
B. 1
C. 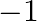
D. none of these
Solution: Option(B) To find: Value of $\left|\begin{array}{ccc}1 & 1+p & 1+p+q \\ 2 & 3+2 p & 1+3 p+2 q \\ 3 & 6+3 p & 1+6 p+3 q\end{array}\right|$ We have,...
Mark the tick against the correct answer in the following: 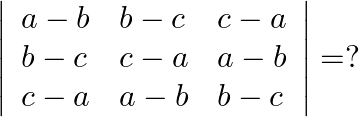
A. 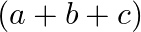
B. 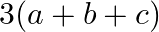
C. 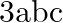
D. 0
Solution: Option(D) To find: Value of $\left|\begin{array}{lll}a-b & b-c & c-a \\ b-c & c-a & a-b \\ c-a & a-b & b-c\end{array}\right|$ We have, $\left|\begin{array}{lll}a-b...
Mark the tick against the correct answer in the following: 
A. 2
B. 6
C. 24
D. 120
Solution: Option(24) To find: Value of $\left|\begin{array}{lll}1 ! & 2 ! & 3 ! \\ 2 ! & 3 ! & 4 ! \\ 3 ! & 4 ! & 5 !\end{array}\right|$ We have,...
Mark the tick against the correct answer in the following: 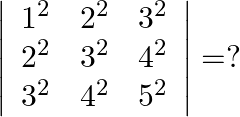
A. 8
B. 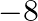
C. 16
D. 142
Solution: Option(A) To find: Value of $\left|\begin{array}{lll}1^{2} & 2^{2} & 3^{2} \\ 2^{2} & 3^{2} & 4^{2} \\ 3^{2} & 4^{2} & 5^{2}\end{array}\right|$ We have,...
Mark the tick against the correct answer in the following: If 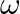 is a complex cube root of unity then the value of
is a complex cube root of unity then the value of  is
is
A. 2
B. 4
C. 0
D. 
Solution: Option(0) To find: Value of $\left|\begin{array}{ccc}1 & \omega & 1+\omega \\ 1+\omega & 1 & \omega \\ \omega & 1+\omega & 1\end{array}\right|$ Formula used: (i)...
Mark the tick against the correct answer in the following: If  is a complex root of unity then
is a complex root of unity then 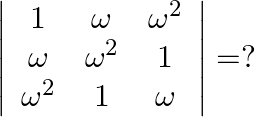
A. 1
B. 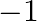
C. 0
D. none of these
Solution: Option(C) To find: Value of $\left|\begin{array}{ccc}1 & \omega & \omega^{2} \\ \omega & \omega^{2} & 1 \\ \omega^{2} & 1 & \omega\end{array}\right|$ We have,...
Mark the tick against the correct answer in the following: 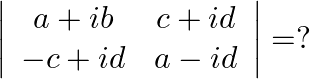
A. 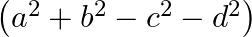
B. 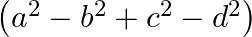
C. 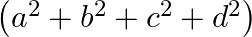
D. none of these
Solution: Option(C) To find: Value of $\left|\begin{array}{cc}a+i b & c+i d \\ -c+i d & a-i b\end{array}\right|$ Formula used: $\mathrm{i}^{2}=-1$ We have, $\left|\begin{array}{cc}a+i b...
Mark the tick against the correct answer in the following: 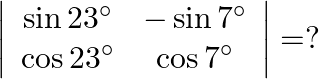
A. 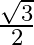
B. 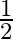
C. 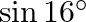
D. 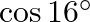
Solution: Option(B) To find: Value of $\left|\begin{array}{cc}\sin 23^{\circ} & -\sin 7^{\circ} \\ \cos 23^{\circ} & \cos 7^{\circ}\end{array}\right|$ Formula used: (i) $\sin (A+B)=\sin A...
Mark the tick against the correct answer in the following: 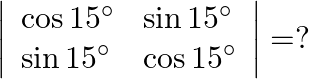
A. 1
B. 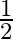
C. 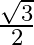
D. none of these
Solution: Option(C) To find: Value of $\left|\begin{array}{ll}\cos 15^{\circ} & \sin 15^{\circ} \\ \sin 15^{\circ} & \cos 15^{\circ}\end{array}\right|$ Formula used: (i) $\cos (A+B)=\cos A...
Mark the tick against the correct answer in the following: 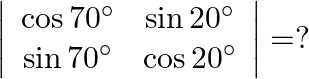
A. 1
B. 0
C. 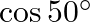
8D. 
Solution: Option(B) To find: Value of $\left|\begin{array}{cc}\cos 70^{\circ} & \sin 20^{\circ} \\ \sin 70^{\circ} & \cos 20^{\circ}\end{array}\right|$ Formula used: (i) $\cos \theta=\sin...
If the points 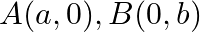 and
and 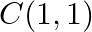 are collinear, prove that
are collinear, prove that 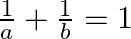
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
If 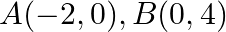 and
and 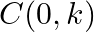 be three points such that area of a
be three points such that area of a 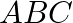 is 4 sq units, find the value of
is 4 sq units, find the value of  .
.
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the value of  for which the area of a ABC having vertices
for which the area of a ABC having vertices 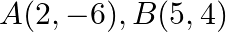 and
and 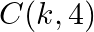 is 35 sq units.
is 35 sq units.
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the value of  for which the points
for which the points 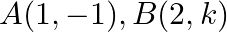 and
and 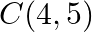 are collinear.
are collinear.
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the value of  for which the points
for which the points 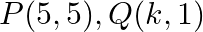 and
and 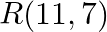 are collinear.
are collinear.
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the value of  for which the points
for which the points 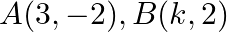 and
and 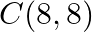 are collinear.
are collinear.
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Use determinants to show that the following points are collinear. 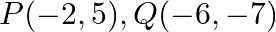 and
and 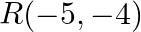
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Use determinants to show that the following points are collinear. 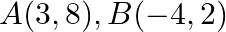 and
and 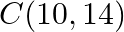
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Use determinants to show that the following points are collinear. 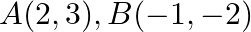 and
and 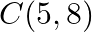
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the area of the triangle whose vertices are: 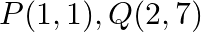 and
and 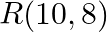
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the area of the triangle whose vertices are: 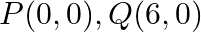 and
and 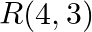
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the area of the triangle whose vertices are: 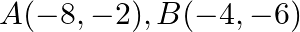 and
and 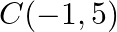
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the area of the triangle whose vertices are: 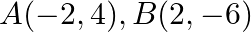 and
and 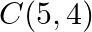
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the area of the triangle whose vertices are: 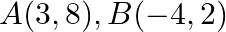 and
and 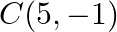
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the principal value of each of the following : 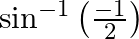
Solution: $\sin ^{-1}\left(\frac{-1}{2}\right)=-\sin ^{-1}\left(\frac{1}{2}\right)\left[\right.$ Formula: $\left.\sin ^{-1}(-x)=\sin ^{-1}(x)\right]$ $=-\frac{\pi}{6}$
Two different dice are rolled simultaneously. Find the probability that the sum o f the numbers on the two dice Is 10.
Solution: When two different dice are thrown, the total number of outcomes = 36. Let E1 be the event of getting the sum of the numbers on the two dice is 10. These numbers are (4 ,6), (5,5)...
A die is thrown three times, find the probability that 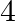 appears on the third toss if it is given that
appears on the third toss if it is given that 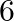 and
and 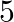 appear respectively on first two tosses.
appear respectively on first two tosses.
As per the given question, $n\;(A)\;=\;36$ And, let $B$ be the event of $6\;and\;5$ appearing respectively on first two tosses, if the die is tossed three times
a) Consider the circuit in the figure. How much energy is absorbed by electrons from the initial state of no current to the state of drift velocity? b) Electrons give up energy at the rate of RI2 per second to the thermal energy. What time scale would one associate with energy in problem a) n = no of electron/volume = 1029/m3, length of circuit = 10 cm, cross-section = A = 1mm2
a) Current is given as I = V/R from the Ohm’s law Therefore, I = 1A But, I = ne Avd vd = I/neA When the values for the above parameters are substituted, vd = 1/1.6 × 10-4 m/s The KE = (KE of one...
In an experiment with a potentiometer, VB = 10V. R is adjusted to be 50 Ω. A student wanting to measure voltage E1 of a battery finds no null point possible. He then diminishes R to 10 Ω and is able to locate the null point on the last segment of the potentiometer. Find the resistance of the potentiometer wire and potential drop per unit length across the wire in the second case.
Equivalent resistance of the potentiometer = 50 Ohm + R’ Equivalent voltage across the potentiometer = 10 V Current through the main circuit I = 10/(50 Ohms +R’) Potential difference across wire of...
A room has AC run for 5 hours a day at a voltage of 220V. The wiring of the room consists of Cu of 1 mm radius and a length of 10 m. Power consumption per day is 10 commercial units. What fraction of it goes in the joule heating in wires? What would happen if the wiring is made of aluminium of the same dimensions?
Power consumption in a day = 10 units Power consumption per hour = 2 units Power consumption = 2 units = 2 kW = 2000 J/s Power consumption in resistors, P = VI Which gives I = 9A We know that...
Two cells of voltage 10V and 2V and internal resistances 10Ω and 5Ω respectively are connected in parallel with the positive end of the 10V battery connected to the negative pole of 2V battery. Find the effective voltage and effective resistance of the combination.
Kirchhoff’s law is applied at c, I1 = I + I2 Kirchhoff’s law is applied at efbae, 10 – IR – 10I2 = 0 10 = IR + 10I1 Kirchhoff’s law is applied at cbadc, -2-IR+5I2 = 0 2 = 5I2- RI I2 = I1 – I...
Suppose there is a circuit consisting of only resistances and batteries and we have to double all voltages and all resistances. Show that currents are unaltered.
Reff is the equivalent internal resistance of the battery Veff is the equivalent voltage of the battery Using Ohm’s law, I = Veff/(Reff + R) When the resistance and effective voltage are increased...
Two conductors are made of the same material and have the same length. Conductor A is a solid wire of diameter 1 mm. Conductor B is a hollow tube of outer diameter 2 mm and inner diameter 1 mm. Find the ratio of resistance RA to RB.
Resistance of wire R = ρ l/A Where A is the cross-sectional area of the conductor L is the length of the conductor ρ is the specific resistance RA = ρl/π(10-3 × 0.5)2 RB = ρl/ π[10-3)2 × (0.5 ×...
Two cells of same emf E but internal resistance r1 and r2 are connected in series to an external resistor R. What should be the value of R so that the potential difference across the terminals of the first cell becomes zero.
Effective emf of two cells = E + E = 2E Effective resistance = R + r1 + r2 Electric current is given as I = 2E/R+r1+r2 Potential difference is given as V1 – E – Ir1 = 0 Which f=gives R = r1 –...
The circuit in the figure shows two cells connected in opposition to each other. Cell E1 is of emf 6V and internal resistance 2Ω; the cell E2 is of emf 4V and internal resistance 8 Ω. Find the potential difference between the points A and B.
Applying Ohm’s law, equivalent emf of the two cells = 6 – 4 = 2V Equivalent resistance = 2 + 8 = 10 Ω Electric current, I = 6-4/2+8 = 0.2A When the loop is considered in the anti-clockwise...
An infinitely long cylinder of radius R is made of an unusual exotic material with refractive index –1. The cylinder is placed between two planes whose normals are along the y-direction. The centre of the cylinder O lies along the y-axis. A narrow laser beam is directed along the y-direction from the lower plate. The laser source is at a horizontal distance x from the diameter in the y-direction. Find the range of x such that light emitted from the lower plane does not reach the upper plane.
The refractive index of the cylinder is -1 and is placed in the air of μ = 1 AB is incident at B to the cylinder such that θr will be negative θ1= θi = θr Total deviation of the outcoming ray is...
If light passes near a massive object, the gravitational interaction causes a bending of the ray. This can be thought of as happening due to a change in the effective refractive index of the medium given by n(r) = 1 + 2 GM/rc2 where r is the distance of the point of consideration from the centre of the mass of the massive body, G is the universal gravitational constant, M the mass of the body and c the speed of light in vacuum. Considering a spherical object find the deviation of the ray from the original path as it grazes the object.
n(r) = 1 + 2GM/rc2
The mixture a pure liquid and a solution in a long vertical column (i.e, horizontal dimensions << vertical dimensions) produces diffusion of solute particles and hence a refractive index gradient along the vertical dimension. A ray of light entering the column at right angles to the vertical deviates from its original path. Find the deviation in travelling a horizontal distance d << h, the height of the column.
Let the height of the long vertical column with transparent liquid be h and dx be the thickness The angle at which the ray AB enters is θ Let y be the new height of the liquid (θ + d θ) is the...
A myopic adult has a far point at 0.1 m. His power of accomodation is 4 diopters. (i) What power lenses are required to see distant objects? (ii) What is his near point without glasses? (iii) What is his near point with glasses? (Take the image distance from the lens of the eye to the retina to be 2 cm.)
i) Power lenses are required to see distant objects 1/f = 1/v – 1/u 1/f = 1/10 f = -10 cm = -0.1 m P = 1/f P = 1/(-0.1) P = -10 diopter ii) When no corrective lens used Pn = Pf + Pa u = -10 cm =...
In many experimental set-ups the source and screen are fixed at a distance say D and the lens is movable. Show that there are two positions for the lens for which an image is formed on the screen. Find the distance between these points and the ratio of the image sizes for these two points.
u = -x1 v = +(D – x1) 1/D – x1 – 1/(-x1) = 1/f u = -x2 v = +(D – x2) 1/D – x2 – 1/(-x2) = 1/f D = x1 + x2 d = x2 – x1 x1 = D – d/2 D – x1 = D + d/2 u = D/2 + d/2 v = D/2 – d/2 m1 = D – d/D + d m2/m1...
A thin convex lens of focal length 25 cm is cut into two pieces 0.5 cm above the principal axis. The top part is placed at (0,0) and an object placed at (–50 cm, 0). Find the coordinates of the image.
1/v = 1/u + 1/f = 1/-50 + 1/25 = 1/50 v = 50 cm Magnification is m = v/u = -50/50 = -1 Therefore, the coordinates of the image are (50 cm, -1 cm) ...
A circular disc of radius ‘R’ is placed co-axially and horizontally inside an opaque hemispherical bowl of radius ‘a’. The far edge of the disc is just visible when viewed from the edge of the bowl. The bowl is filled with transparent liquid of refractive index µ and the near edge of the disc becomes just visible. How far below the top of the bowl is the disc placed?
Distance at which the bowl should be placed in the disc is given as: d = μ(a2 – b2)/√(a + r)2 – μ(a – r)2
There are certain material developed in laboratories which have a negative refractive index (Fig. 9.3). A ray incident from the air (medium 1) into such a medium (medium 2) shall follow a path given by
Answer: (a) The speed of the car in the rear is 65 km h–1. Negative refractive index materials react to Snell's law in the exact opposite direction. When a...
You are given four sources of light each one providing a light of a single colour- red, blue, green, and yellow. Suppose the angle of refraction for a beam of yellow light corresponding to a particular angle of incidence at the interface of two media is 90o. Which of the following statements is correct if the source of yellow light is replaced with that of other lights without changing the angle of incidence?
a) the beam of red light would undergo total internal reflection
b) the beam of red light would bend towards normal while it gets refracted through the second medium
c) the beam of blue light would undergo total internal reflection
d) the beam of green light would bend away from the normal as it gets refracted through the second medium
Answer: c) the beam of blue light would undergo total internal reflection
A ray of light incident at an angle θ on a refracting face of a prism emerges from the other face normally. If the angle of the prism is 5o and the prism is made of a material of refractive index 1.5, the angle of incidence is
a) 7.5o
b) 5o
c) 15o
d) 2.5o
Answer: a) 7.5o The distance between the refracting surfaces is negligible with thin prisms, thus the prism angle (A) is very small. Because A = r1 + r2, if A is tiny, both r1 and r2 will be little...
Two cells of same emf E but internal resistance r1 and r2 are connected in series to an external resistor R. What should be the value of R so that the potential difference across the terminals of the first cell becomes zero.
Effective emf of two cells = E + E = 2E Effective resistance = R + r1 + r2 Electric current is given as I = 2E/R+r1+r2 Potential difference is given as V1 – E – Ir1 = 0 Which f=gives R = r1 –...
Let there be n resistors R1……..Rn with Rmax = max(R1……Rn) and Rmin = min(R1…….Rn). Show that when they are connected in parallel, the resultant resistance Rp < Rmin and when they are connected in series, the resultant resistance Rs > Rmax. Interpret the result physically.
The current is represented as I = E/R+nR when the resistors are connected in series. Current is expressed as 10I = E/(R+R/n) when the resistors are connected in parallel....
First, a set of n equal resistors of R each are connected in series to a battery of emf E and internal resistance R. A current I is observed to flow. Then the n resistors are connected in parallel to the same battery. It is observed that the current is increased 10 times. What is ‘n’?
The current is represented as I = E/R+nR when the resistors are connected in series. Current is expressed as 10I = E/(R+R/n) when the resistors are connected in parallel. We get n = 10 by solving...
. A cell of emf E and internal resistance r is connected across an external resistance R. Plot a graph showing the variation of PD across R versus R.
The graphic depiction is as follows: The resistance r is connected across the external resistance R, and E is the cell's emf. V = ER/R+r is the connection between voltage and R....
While doing an experiment with potentiometer it was found that the deflection is one-sided and i) the deflection decreased while moving from one end A of the wire to the end B; ii) the deflection increased, while the jockey was moved towards the end B. i) Which terminal +ve or –ve of the cell E, is connected at X in case
i) and how is E1 related to E?
ii) Which terminal of the cell E1 is connected at X in case ii)?
The positive terminal of cell E1 is linked to E, and E is connected to X. Furthermore, E1 > E ii) cell E1's negative terminal is linked to X.
Power P is to be delivered to a device via transmission cables having resistance Rc. If V is the voltage across R and I the current through it, find the power wasted and how can it be reduced.
P = i2Rc is the power utilised by transmission lines. The resistance of connecting wires is denoted by Rc. P = VI is the formula for calculating power. Power...
Power P is to be delivered to a device via transmission cables having resistance Rc. If V is the voltage across R and I the current through it, find the power wasted and how can it be reduced.
Power consumed by the transmission lines is given as P = i2Rc. Where Rc is the resistance of connecting cables. Power is given as P = VI. The transmission of power takes places either during low...
Why are alloys used for making standard resistance coils?
Alloys are used in the making of the standard resistance coils because they have less temperature coefficient of resistance and the temperature sensitivity is also less.
For wiring in the home, one uses Cu wires or Al wires. What considerations are involved in this?
The main considerations in the selection of the wires is the conductivity of the metal, cost of metal, and their availability.
What is the advantage of using thick metallic strips to join wires in a potentiometer?strips to join wires in a potentiometer?
The advantage of using thick metallic strips is that the resistance of these strips is negligible.
What are the advantages of the null-point method in a Wheatstone bridge? What additional measurements would be required to calculate R unknown by any other?
The advantage of a null-point in the Wheatstone bridge is that the resistance of the galvanometer is not affected by the balance point. The R unknown is calculated by using Kirchhoff’s rule.
The relaxation time τ is nearly independent of applied E field whereas it changes significantly with temperature T. First fact is responsible for Ohm’s law whereas the second fact leads to a variation of ρ with temperature. Elaborate why?
Relaxation time is the time interval between two successive collisions of the electrons.It is defined asτ = mean free path/rms velocity of electrons usually, the drift velocity of the electrons is...
Is the momentum conserved when charge crosses a junction in an electric circuit? Why or why not?
The momentum is not conserved when the charge crosses a junction in an electric circuit. This is because the drift velocity is proportional to the electric field.
Temperature dependence of resistivity ρ(T) of semiconductors, insulators, and metals is significantly based on the following factors:
a) number of charge carriers can change with temperature T
b) time interval between two successive collisions can depend on T
c) length of material can be a function of T
d) mass of carriers is a function of T
The correct answer is a) number of charge carriers can change with temperature T b) time interval between two successive collisions can depend on T
In a meter bridge, the point D is a neutral point.
a) the meter bridge can have no other neutral point for this set of resistances
b) when the jockey contacts a point on meter wire left of D, current flows to B from the wire
c) when the jockey contacts a point on a meter wire to the right of D, current flows from B to the wire through the galvanometer
d) when R is increased, the neutral point shifts to left
The correct answer is a) the meter bridge can have no other neutral point for this set of resistances c) when the jockey contacts a point on a meter wire to the right of D, current flows from B to...
Temperature dependence of resistivity ρ(T) of semiconductors, insulators, and metals is significantly based on the following factors:
a) number of charge carriers can change with temperature T
b) time interval between two successive collisions can depend on T
c) length of material can be a function of T
d) mass of carriers is a function of T
solution:The correct answer is a) number of charge carriers can change with temperature T b) time interval between two successive collisions can depend on T
Consider a simple circuit in the figure.stands for a variable resistance R’.
R’ can vary from R0 to infinity. r is internal resistance of the battery,
a) potential drop across AB is nearly constant as R’ is varied
b) current through R’ is nearly a constant as R’ is varied
c) current I depends sensitively on R’
d) I ≥V/r+R always
solution: The correct answer is a) potential drop across AB is nearly constant as R’ is varied d) I ≥V/r+R always
Kirchhoff’s junction rule is a reflection of
a) conservation of current density vector
b) conservation of charge
c) the fact that the momentum with which a charged particle approaches a junction is unchanged as the charged particle leaves the junction
d) the fact that there is no accumulation of charges at a junction
solution: The correct answer is b) conservation of charge d) the fact that there is no accumulation of charges at a junction
Which of the following characteristics of electrons determines the current in a conductor?
v a) drift velocity alone
b) thermal velocity alone
c) both drift velocity and thermal velocity
d) neither drift nor thermal velocity
solution: The correct answer is a) drift velocity alone
A metal rod of length 10 cm and a rectangular cross-section of 1 cm × 1/2 cm is connected to battery across opposite faces. The resistance will be
a) maximum when the battery is connected across 1 cm × 1/2 cm faces
b) maximum when the battery is connected across 10 cm × 1 cm faces
c) maximum when the battery is connected across 10 cm × 1/2 cm faces
d) same irrespective of the three faces
solution:The correct solution is a) maximum when the battery is connected across 1 cm × 1/2 cm faces
Two cells of emf’s approximately 5V and 10V are to be accurately compared using a potentiometer of length 400 cm.
a) the battery that runs the potentiometer should have voltage of 8V
b) the battery of potentiometer can have a voltage of 15V and R adjusted so that the potential drop across the wire slightly exceeds 10V
c) the first portion of 50 cm of wire itself should have a potential drop of 10V
d) potentiometer is usually used for comparing resistances and not voltages
Solution: The correct solution is b) the potentiometer's battery can be set to 15V and R adjusted so that the potential drop across the wire is a little higher than 10V.
A resistance R is to be measured using a meter bridge. Student chooses the standard resistance S to be 100Ω. He finds the null point at l1 = 2.9 cm . He is told to attempt to improve the accuracy. Which of the following is a useful way?
a) he should measure l1 more accurately
b) he should change S to 1000 Ω and repeat the experiment
c) he should change S to 3 Ω and repeat the experiment
d) he should give up hope of a more accurate measurement with a meter bridge
solution:The correct answer is c) he should change S to 3 Ω and repeat the experiment
Two batteries of emf ε1 and ε2 and internal resistances r1 and r2 respectively are connected in parallel as shown in the figure.a) the equivalent emf εeq of the two cells is between ε1 and ε2 that is ε1 < εeq < ε2
b) the equivalent emf εeq is smaller than ε1
c) the εeq is given by εeq = ε1 + ε2 always
d) εeq is independent of internal resistances r1 and r2
solution: The correct answer is a) the equivalent emf εeq of the two cells is between ε1 and ε2 that is ε1 < εeq < ε2
Consider a current-carrying wire in the shape of a circle. Note that as the current progresses along the wire, the direction of j changes in an exact manner, while the current I remain unaffected. The agent that is essentially responsible for is
a) source of emf
b) electric field produced by charges accumulated on the surface of wire
c) the charges just behind a given segment of wire which push them just the right way by repulsion
d) the charges ahead
solution: The correct answer is b) electric field produced by charges accumulated on the surface of wire
Graph the solution sets of the following inequations: 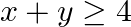
Given $x+y \geq 4$ $\Rightarrow y \geq 4-x$ Consider the equation $y=4-x$. Finding points on the coordinate axes: If $x=0$, the $y$ value is 4 i.e, $y=4$ $\Rightarrow$ the point on the $Y$ axis is...
Show that 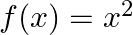 is continues at
is continues at 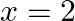
Solution: L.H.L.: $\lim _{x \rightarrow 2-} f(x)=\lim _{x \rightarrow 2-} x^{2}$ $=4$ R.H.L.: $\lim _{\mathrm{x} \rightarrow 2^{*}} \mathrm{f}(\mathrm{x})=\lim _{\mathrm{x} \rightarrow 2^{*}}...
(i) 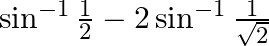
(ii) 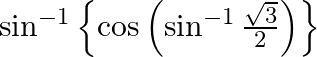
Solution: (i) We can write the given question as, $\sin ^{-1} \frac{1}{2}-2 \sin ^{-1} \frac{1}{\sqrt{2}}=\sin ^{-1} \frac{1}{2}-\sin ^{-1}\left(2 \times \frac{1}{\sqrt{2}}...
Find the principal value of the following:
(i) 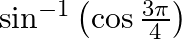
(ii) 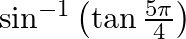
Solution: (i) Suppose $\sin ^{-1}\left(\cos \frac{3 \pi}{4}\right)=\mathrm{y}$ Therefore we can write the above equation as $\sin \mathrm{y}=\cos \frac{3 \pi}{4}=-\sin \left(\pi-\frac{3...
Find the principal value of the following:
(i) 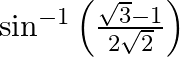
(ii) 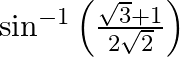
Solution: (i) It is given that functions can be written as $\sin ^{-1}\left(\frac{\sqrt{3}-1}{2 \sqrt{2}}\right)=\sin ^{-1}\left(\frac{\sqrt{3}}{2 \sqrt{2}}-\frac{1}{2 \sqrt{2}}\right) $Taking $1 /...
Find the principal value of the following:
(i) 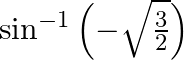
(i i) 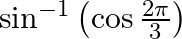
Solution: $(i)$ Let $\sin ^{-1}\left(\frac{-\sqrt{3}}{2}\right)=y$ Therefore $\sin y=\left(\frac{-\sqrt{3}}{2}\right)$ $\begin{array}{l} =-\sin \left(\frac{\pi}{3}\right) \\ =\sin...
A manufacturer produces two Models of bikes – Model 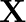 and Model
and Model 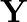 . Model
. Model 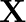 takes 6 man-hours to make per unit, while Model Y takes 10 man-hours per unit. There is a total of 450 man-hour available per week. Handling and Marketing costs are Rs 2000 and Rs 1000 per unit for Models
takes 6 man-hours to make per unit, while Model Y takes 10 man-hours per unit. There is a total of 450 man-hour available per week. Handling and Marketing costs are Rs 2000 and Rs 1000 per unit for Models 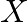 and
and 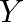 respectively. The total funds available for these purposes are Rs 80,000 per week. Profits per unit for Models
respectively. The total funds available for these purposes are Rs 80,000 per week. Profits per unit for Models 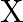 and
and 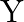 are Rs 1000 and Rs 500 , respectively. How many bikes of each model should the manufacturer produce so as to yield a maximum profit? Find the maximum profit.
are Rs 1000 and Rs 500 , respectively. How many bikes of each model should the manufacturer produce so as to yield a maximum profit? Find the maximum profit.
Solution: Let us take $\mathrm{x}$ an $\mathrm{y}$ to be the no. of models of bike produced by the manufacturer. From the question we have, Model $x$ takes 6 man-hours to make per unit Model $y$...
Maximize 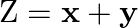 subject to
subject to 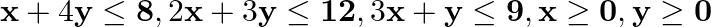 .
.
Solution: It is given that: $Z=x+y$ subject to constraints, $x+4 y \leq 8$ $2 x+3 y \leq 12,3 x+y \leq 9, x \geq 0, y \geq 0$ Now construct a constrain table for the above, we have Here, it can be...
Refer to Exercise 15. Determine the maximum distance that the man can travel.
Solution: According to the solution of exercise 15, we have Maximize $Z=x+y$, subject to the constraints $2 x+3 y \leq 120 \ldots$ (i) $8 x+5 y \leq 400 \ldots$ (ii) $x \geq 0, y \geq 0$ Let's...
Refer to Exercise 14. How many sweaters of each type should the company make in a day to get a maximum profit? What is the maximum profit?
Solution: According to the solution of exercise 14, we have Maximize $Z=200 x+120 y$ subject to constrains $\begin{array}{l} 3 x+y \leq 600 \ldots \text { (i) } \\ x+y \leq 300 \ldots \text { (ii) }...
Refer to Exercise 13. Solve the linear programming problem and determine the maximum profit to the manufacturer.
Solution: According to the solution of exercise 13, we have The objective function for maximum profit $\mathrm{Z}=100 \mathrm{x}+170 \mathrm{y}$ Subject to constraints, $x+4 y \leq 1800 \ldots(i)$...
Refer to Exercise 12. What will be the minimum cost?
Solution: According to the solution of exercise 12, we have The objective function for minimum cost is $\mathrm{Z}=400 \mathrm{x}+200 \mathrm{y}$ Subject to the constrains; $5 x+2 y \geq 30 \ldots...
Refer to Exercise 11. How many of circuits of Type A and of Type B, should be produced by the manufacturer so as to maximize his profit? Determine the maximum profit.
Solution: According to the solution of exercise 11, we have Maximize $Z=50 x+60 y$ subject to the constraints $20 x+10 y \leq 2002 x+y \leq 20 \ldots$ (i) $10 x+20 y \leq 120 x+2 y \leq 12 \ldots$...
A man rides his motorcycle at the speed of 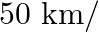 hour. He has to spend Rs 2 per km on petrol. If he rides it at a faster speed of
hour. He has to spend Rs 2 per km on petrol. If he rides it at a faster speed of 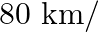 hour, the petrol cost increases to Rs 3 per km. He has at most Rs 120 to spend on petrol and one hour’s time. He wishes to find the maximum distance that he can travel. Express this problem as a linear programming problem.
hour, the petrol cost increases to Rs 3 per km. He has at most Rs 120 to spend on petrol and one hour’s time. He wishes to find the maximum distance that he can travel. Express this problem as a linear programming problem.
Solution: Suppose the man covers $\mathrm{x} \mathrm{km}$ on his motorcycle at the speed of $50 \mathrm{~km} / \mathrm{hr}$ and covers $\mathrm{y} \mathrm{km}$ at the speed of $50 \mathrm{~km} /...
A company manufactures two types of sweaters: type A and type B. It costs Rs 360 to make a type A sweater and Rs 120 to make a tvpe B sweater. The companv can make at most 300 sweaters and spend at most Rs 72000 a day. The number of sweaters of type B cannot exceed the number of sweaters of type A by more than 100 . The company makes a profit of Rs 200 for each sweater of type A and Rs 120 for every sweater of type B. Formulate this problem as a LPP to maximize the profit to the company.
Solution: Suppose $\mathrm{x}$ and $\mathrm{y}$ to be the number of sweaters of type $\mathrm{A}$ and type $\mathrm{B}$ respectively. The following constraints are: $360 x+120 y \leq 72000...
A company manufactures two types of screws A and B. All the screws have to pass through a threading machine and a slotting machine. A box of Type A screws requires 2 minutes on the threading machine and 3 minutes on the slotting machine. A box of type  screws requires 8 minutes of threading on the threading machine and 2 minutes on the slotting machine. In a week, each machine is available for 60 hours. On selling these screws, the company gets a profit of Rs 100 per box on type A screws and Rs 170 per box on type B screws. Formulate this problem as a LPP given that the objective is to maximize profit.
screws requires 8 minutes of threading on the threading machine and 2 minutes on the slotting machine. In a week, each machine is available for 60 hours. On selling these screws, the company gets a profit of Rs 100 per box on type A screws and Rs 170 per box on type B screws. Formulate this problem as a LPP given that the objective is to maximize profit.
Solution: Suppose that the company manufactures $\mathrm{x}$ boxes of type A screws and $y$ boxes of type B screws. The below table is constructed from the information provided:...
A firm has to transport 1200 packages using large vans which can carry 200 packages each and small vans which can take 80 packages each. The cost for engaging each large van is Rs 400 and each small van is Rs 200 . Not more than Rs 3000 is to be spent on the iob and the number of large vans cannot exceed the number of small vans. Formulate this problem as a LPP given that the objective is to minimize cost.
Solution: Suppose $\mathrm{x}$ and $\mathrm{y}$ to be the number of large and small vans respectively. The below constrains table is constructed from the information provided:...
A manufacturer of electronic circuits has a stock of 200 resistors, 120 transistors and 150 capacitors and is required to produce two types of circuits A and B. Type A requires 20 resistors, 10 transistors and 10 capacitors. Type B requires 10 resistors, 20 transistors and 30 capacitors. If the profit on type A circuit is Rs 50 and that on type B circuit is Rs 60 , formulate this problem as a LPP so that the manufacturer can maximize his profit.
Solution: Suppose $\mathrm{x}$ units of type A and $y$ units of type $\mathrm{B}$ electric circuits be produced by the manufacturer. The table is constructed from the information provided:...
In Fig. 12.11, the feasible region (shaded) for a LPP is shown. Determine the maximum and minimum value of 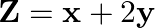
Solution: It is seen from the given figure, that the corner points are as follows: $\mathrm{R}(7 / 2,3 / 4), \mathrm{Q}(3 / 2,15 / 4), \mathrm{P}(3 / 13,24 / 13)$ and $\mathrm{S}(18 / 7,2 / 7)$ On...
The feasible region for a LPP is shown in Fig. 12.10. Evaluate 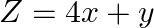 at each of the corner points of this region. Find the minimum value of
at each of the corner points of this region. Find the minimum value of 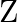 , if it exists.
, if it exists.
Solution: It is given that: $Z=4 x+y$ In the figure given, $\mathrm{ABC}$ is the feasible region which is open unbounded. Here, we get $x+y=3\dots \dots(i)$ and $\quad x+2 y=4 \quad \ldots$ (ii) On...
Refer to Exercise 7 above. Find the maximum value of 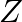 .
.
Solution: It is clearly seen that the evaluating table for the value of $Z$, the maximum value of $Z$ is 47 at $(3,2)$
The feasible region for a LPP is shown in Fig. 12.9. Find the minimum value of 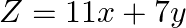 .
.
Solution: It is seen from the given figure, that the feasible region is $\mathrm{ABCA}$. Corner points are $\mathrm{C}(0,3), \mathrm{B}(0,5)$ and for A, we have to solve equations $x+3 y=9$ and...
Feasible region (shaded) for a LPP is shown in Fig. 12.8. Maximize 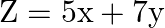 .
.
Solution: It is given that: $\mathrm{Z}=5 \mathrm{x}+7 \mathrm{y}$ and feasible region $\mathrm{OABC}$. Corner points of the feasible region are $\mathrm{O}(0,0), \mathrm{A}(7,0), \mathrm{B}(3,4)$...
Determine the maximum value of 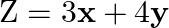 if the feasible region (shaded) for a LPP is shown in Fig. 12.7.
if the feasible region (shaded) for a LPP is shown in Fig. 12.7.
Solution: OAED is the feasible region, as shown in the figure At $A, y=0$ in eq. $2 x+y=104$ we obtain, $\mathrm{x}=52$ This is a corner point $A=(52,0)$ At $D, x=0$ in eq. $x+2 y=76$ we obtain,...
Minimize 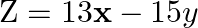 subject to the constraints:
subject to the constraints: 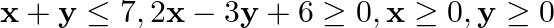 .
.
Solution: It is given that: $\mathrm{Z}=13 \mathrm{x}-15 \mathrm{y}$ and the constraints $\mathrm{x}+\mathrm{y} \leq 7$, $2 x-3 y+6 \geq 0, x \geq 0, y \geq 0$ Taking $x+y=7$, we have...
Maximize the function 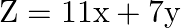 , subject to the constraints:
, subject to the constraints: 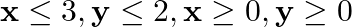
Solution: It is given that: $\mathrm{Z}=\mathrm{Z}=11 \mathrm{x}+7 \mathrm{y}$ and the constraints $\mathrm{x}$ $\leq 3, y \leq 2, x \geq 0, y \geq 0$ Plotting all the constrain equations it can be...
Maximize 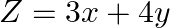 , subject to the constraints:
, subject to the constraints: 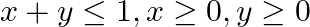
Solution: It is given that: $Z=3 x+4 y$ and the constraints $x+y \leq 1, x \geq 0$ $\mathrm{y} \geq 0$ Taking $x+y=1$, we have $$\begin{tabular}{|l|l|l|} \hline$x$ & 1 & 0 \\ \hline$y$ & 0 & 1 \\...
Determine the maximum value of 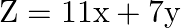 subject to the constraints:
subject to the constraints: 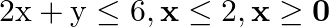
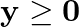
Solution: It is given that: $\mathrm{Z}=11 \mathrm{x}+7 \mathrm{y}$ and the constraints $2 \mathrm{x}+\mathrm{y} \leq 6, \mathrm{x} \leq 2, \mathrm{x} \geq 0, \mathrm{y} \geq 0$ Let $2 x+y=6$...
In the following cases, find the distance of each of the given points from the corresponding given plane. Point Plane
(a) (2, 3, -5) x + 2y – 2z = 9
(b) (-6, 0, 0) 2x – 3y + 6z – 2 = 0
Solution: (a) The length of perpendicular from the point $(2,3,-5)$ on the plane $x+2 y-2 z=9 \Rightarrow x+2 y-2 z-9=0$ is $\frac{\left|a x_{1}+b y_{1}+c z_{1}+d\right|}{\sqrt{a^{2}+b^{2}+c^{2}}}$...
In the following cases, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them.
(a) 4x + 8y + z – 8 = 0 and y + z – 4 = 0
Solution: (a) $4 x+8 y+z-8=0$ and $y+z-4=0$ It is given that The eq. of the given planes are $4 x+8 y+z-8=0 \text { and } y+z-4=0$ It is known to us that, two planes are $\perp$ if the direction...
In the following cases, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them.
(a) 2x – 2y + 4z + 5 = 0 and 3x – 3y + 6z – 1 = 0
(b) 2x – 2y + 4z + 5 = 0 and 3x – 3y + 6z – 1 = 0
Solution: (a) $2 x-2 y+4 z+5=0$ and $3 x-3 y+6 z-1=0$ It is given that The eq. of the given planes are $2 x-2 y+4 z+5=0$ and $x-2 y+5=0$ It is known to us that, two planes are $\perp$ if the...
Find the equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x – y + z = 0.
Solution: Let's say that the eq. of the plane that passes through the two-given planes $x+y+z=1$ and $2 x+3 y+4 z=5$ is $\begin{array}{l} (x+y+z-1)+\lambda(2 x+3 y+4 z-5)=0 \\ (2 \lambda+1) x+(3...
Find the equation of the plane through the intersection of the planes 3x – y + 2z – 4 = 0 and x + y + z – 2 = 0 and the point (2, 2, 1).
Solution: It is given that Eq. of the plane passes through the intersection of the plane is given by $(3 x-y+2 z-4)+\lambda(x+y+z-2)=0$ and the plane passes through the points $(2,2,1)$ Therefore,...
Find the equation of the plane with intercept 3 on the  -axis and parallel to ZOX plane.
-axis and parallel to ZOX plane.
Solution: It is known to us that the equation of the plane $\mathrm{ZOX}$ is $\mathrm{y}=0$ Therefore, the equation of plane parallel to $\mathrm{ZOX}$ is of the form, $\mathrm{y}=\mathrm{a}$ As the...
Find the equations of the planes that passes through three points.
(a) (1, 1, –1), (6, 4, –5), (–4, –2, 3)
(b) (1, 1, 0), (1, 2, 1), (–2, 2, –1)
Solution: (a) It is given that, The points are $(1,1,-1),(6,4,-5),(-4,-2,3)$. Let, $\begin{array}{l} =\left|\begin{array}{ccc} 1 & 1 & -1 \\ 6 & 4 & -5 \\ -4 & -2 & 3...
Find the Cartesian equation of the following planes:
(a) 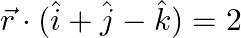
(b) 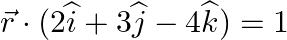
Solution: (a) It is given that, The equation of the plane. Let $\overrightarrow{\mathrm{r}}$ be the position vector of $\mathrm{P}(\mathrm{x}, \mathrm{y}, \mathrm{z})$ is given by $\vec{r}=x...
In each of the following cases, determine the direction cosines of the normal to the plane and the distance from the origin.
(a) 2x + 3y – z = 5
(b) 5y + 8 = 0
Solution: (a) $2 x+3 y-z=5$ It is given that The eq. of the plane, $2 x+3 y-z=5 \ldots$. (1) The direction ratio of the normal $(2,3,-1)$ Using the formula,...
Find the shortest distance between the lines whose vector equations are 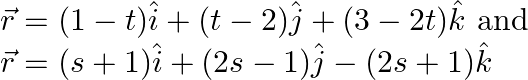
Solution: Consider the given equations $\begin{array}{l} \Rightarrow \vec{r}=(1-t) \hat{i}+(t-2) \hat{j}+(3-2 t) \hat{k} \\ \vec{r}=\hat{i}-t \hat{i}+t \hat{j}-2 \hat{j}+3 \hat{k}-2 t \hat{k} \\...
Find the shortest distance between the lines 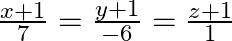 and
and 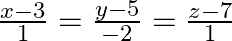
Solution: It is known to us that the shortest distance between two lines $\frac{x+1}{7}=\frac{y+1}{-6}=\frac{z+1}{1}$ and $\frac{x-3}{1}=\frac{y-5}{-2}=\frac{z-7}{1}$ is given as:...
Show that the lines 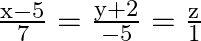 and
and 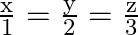 are perpendicular to each other.
are perpendicular to each other.
Solution: The equations of the given lines are $\frac{\mathrm{x}-5}{7}=\frac{\mathrm{y}+2}{-5}=\frac{\mathrm{z}}{1}$ and $\frac{\mathrm{x}}{1}=\frac{\mathrm{y}}{2}=\frac{\mathrm{z}}{3}$ Two lines...
Find the values of p so that the lines 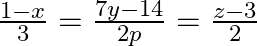 and
and  are at right angles.
are at right angles.
Solution: The standard form of a pair of Cartesian lines is:...
Find the vector and the Cartesian equations of the line that passes through the points (3, –2, –5), (3, –2, 6).
Solution: It is given that Let's calculate the vector form: The vector eq. of as line which passes through two points whose position vectors are $\vec{a}$ and $\vec{b}$ is...
If X is the number of tails in three tosses of a coin, determine the standard deviation of X.
Given, \[X\text{ }=\text{ }0,\text{ }1,\text{ }2,\text{ }3\] P(X = r) \[={{~}^{n}}{{C}_{r}}~{{p}^{r}}~{{q}^{n-r}}\] Where \[n\text{ }=\text{ }3,\text{ }p\text{ }=\text{ 1/2},\text{ }q\text{ }=\text{...
The general solution of the differential equation ![Rendered by QuickLaTeX.com \[{{e}^{x}}~dy\text{ }+\text{ }\left( y\text{ }{{e}^{x}}~+\text{ }2x \right)\text{ }dx\text{ }=\text{ }0\text{ }isA.\text{ }x\text{ }ey\text{ }+\text{ }{{x}^{2}}~=\text{ }C\text{ }B.\text{ }x\text{ }ey\text{ }+\text{ }{{y}^{2}}~=\text{ }C\text{ }C.\text{ }y\text{ }ex\text{ }+\text{ }{{x}^{2}}~=\text{ }C\text{ }D.\text{ }y\text{ }ey\text{ }+\text{ }{{x}^{2}}~=\text{ }C\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a5083fc3f37724ded34eb973899cb501_l3.png)
Therefore, the correct option is option(c).
The general solution of a differential equation of the type is
SOLUTION: Therefore, yje correct option is option(c).
The general solution of the differential equation is ![Rendered by QuickLaTeX.com \[\mathbf{A}.\text{ }\mathbf{xy}\text{ }=\text{ }\mathbf{C}\text{ }\mathbf{B}.\text{ }\mathbf{x}\text{ }=\text{ }\mathbf{C}{{\mathbf{y}}^{\mathbf{2}}}~\mathbf{C}.\text{ }\mathbf{y}\text{ }=\text{ }\mathbf{Cx}\text{ }\mathbf{D}.\text{ }\mathbf{y}\text{ }=\text{ }\mathbf{C}{{\mathbf{x}}^{\mathbf{2}}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1d706555279c605d673ea5651ada04da_l3.png)
Given question is Therefore, the correct option is OPTION(C)
The population of a village increases continuously at the rate proportional to the number of its inhabitants present at any time. If the population of the village was 20, 000 in 1999 and 25000 in the year 2004, what will be the population of the village in 2009?
Find a particular solution of the differential equation, given that y = 0 when x = 0.
Find a particular solution of the differential equation (x ≠ 0), given that y = 0 when x = π/2
Solve the differential equation 
Find a particular solution of the differential equation (x – y) (dx + dy) = dx – dy, given that y = –1, when x = 0. (Hint: put x – y = t)
Solve the differential equation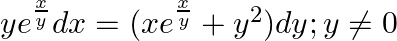
Find the particular solution of the differential equation ![Rendered by QuickLaTeX.com \[\left( \mathbf{1}\text{ }+\text{ }{{\mathbf{e}}^{\mathbf{2x}}} \right)\text{ }\mathbf{dy}\text{ }+\text{ }\left( \mathbf{1}\text{ }+\text{ }{{\mathbf{y}}^{\mathbf{2}}} \right)\text{ }{{\mathbf{e}}^{\mathbf{x}}}~\mathbf{dx}\text{ }=\text{ }\mathbf{0}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a741e3dfd2b281497b24b3de70542d10_l3.png)
, given that y = 1 when x = 0.
Find the equation of the curve passing through the point (0, π/4) whose differential equation is sin x cos y dx + cos x sin y dy = 0.
Show that the general solution of the differential equation is given by (x + y + 1) = A (1 – x – y – 2xy), where A is parameter.
Find the general solution of the differential equation 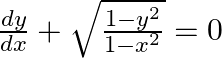
On integrating, we get, ⇒ sin-1x + sin-1y = C
Form the differential equation of the family of circles in the first quadrant which touch the coordinate axes.
(x -a)2 + (y –a)2 = a2 …………1 differentiating eq 1 with respect to x, we get, \[\begin{array}{*{35}{l}} 2\left( x-a \right)\text{ }+\text{ }2\left( y-a \right)\text{ }dy/dx~=\text{ }0 \\ \Rightarrow...
Prove that ![Rendered by QuickLaTeX.com \[{{\mathbf{x}}^{\mathbf{2}}}~-\text{ }{{\mathbf{y}}^{\mathbf{2}}}~=\text{ }\mathbf{c}\text{ }{{\left( {{\mathbf{x}}^{\mathbf{2}}}~+\text{ }{{\mathbf{y}}^{\mathbf{2}}} \right)}^{\mathbf{2}}}~\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3aba527b09857b2a939cd844ff559f93_l3.png)
is the general solution of differential equation ![Rendered by QuickLaTeX.com \[({{\mathbf{x}}^{\mathbf{3}}}-\mathbf{3x}{{\mathbf{y}}^{\mathbf{2}}})\text{ }\mathbf{dx}\text{ }=\text{ }\left( {{\mathbf{y}}^{\mathbf{3}}}-\mathbf{3}{{\mathbf{x}}^{\mathbf{2}}}\mathbf{y} \right)\text{ }\mathbf{dy},\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f17e91ba3477eee6c20ed07cc8909f13_l3.png)
where c is a parameter.
Form the differential equation representing the family of curves given by (x – a)^2 + 2y^2 = a^2, where a is an arbitrary constant.
verify that the given function (implicit or explicit) is a solution of the corresponding differential equation (iii) 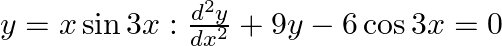 (iv)
(iv) 
verify that the given function (implicit or explicit) is a solution of the corresponding differential equation.(i)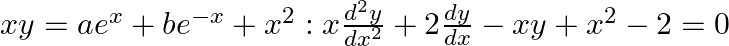 (ii)
(ii) 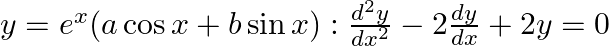
indicate its order and degree (if defined). 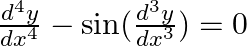
indicate its order and degree (if defined). (i) 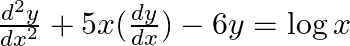 (ii)
(ii) 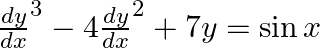
Therefore, its degree is three.
The Integrating Factor of the differential equation 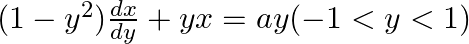 is
is 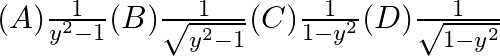
Therefore, the correct option is OPTION(D)
The Integrating Factor of the differential equation is A. e–x B. e–y C. 1/x D. x
Therefore, the correct option is OPTION(C).
Find the equation of a curve passing through the point (0, 2) given that the sum of the coordinates of any point on the curve exceeds the magnitude of the slope of the tangent to the curve at that point by 5.
Thus, equation (2) becomes: \[\begin{array}{*{35}{l}} 0\text{ }+\text{ }2\text{ }-\text{ }4\text{ }=\text{ }C\text{ }{{e}^{0}} \\ \Rightarrow ~C\text{ }=\text{ }-2 \\ \end{array}\] Substituting C...
Find the equation of a curve passing through the origin given that the slope of the tangent to the curve at any point (x, y) is equal to the sum of the coordinates of the point.
Since, the curve passes through origin. Thus, equation 2 becomes 1 = C Substituting C = 1 in equation 2, we get, \[x\text{ }+\text{ }y\text{ }+\text{ }1\text{ }=\text{ }{{e}^{x}}\] Therefore, the...
find a particular solution satisfying the given condition: 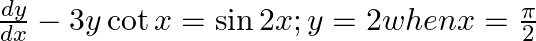
find a particular solution satisfying the given condition: 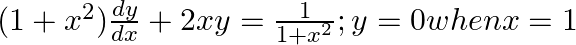
find a particular solution satisfying the given condition: 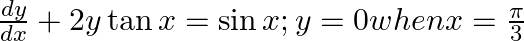
find the general solution: 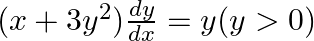
⇒ x = 3y2 + Cy
find the general solution: 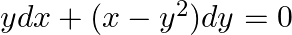
$x=\frac{{{y}^{3}}}{3}+c$ $x=\frac{{{y}^{2}}}{3}+\frac{c}{y}$
find the general solution: 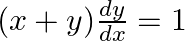
find the general solution: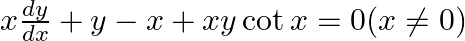
find the general solution: 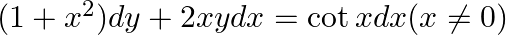
find the general solution: 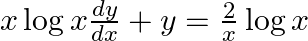
find the general solution: 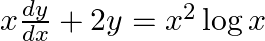
find the general solution: 
find the general solution: 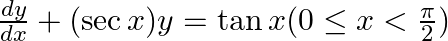
find the general solution: 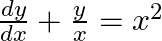
find the general solution: 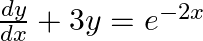
find the general solution: 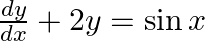
If ![Rendered by QuickLaTeX.com \[\theta \]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-28c6cbc3df8e19af9d0e93bce5df4065_l3.png)
is the angle between any two vectors ![Rendered by QuickLaTeX.com \[\overrightarrow{a}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f875b3d145d74fcad5c39bf1d50af3ef_l3.png)
and ![Rendered by QuickLaTeX.com \[\overrightarrow{b}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-80569b5b72a6d73d223867aa2d36880d_l3.png)
, then ![Rendered by QuickLaTeX.com \[\left| \overrightarrow{a}.\overrightarrow{b} \right|=\left| \overrightarrow{a}\times \overrightarrow{b} \right|\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f4eaf9cf090a16866e02da8ae1036cdb_l3.png)
when ![Rendered by QuickLaTeX.com \[\theta \]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-28c6cbc3df8e19af9d0e93bce5df4065_l3.png)
is equal to (A) ![Rendered by QuickLaTeX.com \[0\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b4f4fbf425b3e7b1e844d7922169d13c_l3.png)
(B) ![Rendered by QuickLaTeX.com \[\frac{\pi }{4}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-971c5664ffae1358e7ee692b1c572379_l3.png)
(C) ![Rendered by QuickLaTeX.com \[\frac{\pi }{2}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-4fd1d21095f8f8c17211b419ebb4d9b0_l3.png)
(D) ![Rendered by QuickLaTeX.com \[\pi \]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-68a8339cbb5250772acfbc5da356942d_l3.png)
![Rendered by QuickLaTeX.com \[\left| \overrightarrow{a}.\overrightarrow{b} \right|=\left| \overrightarrow{a}\times \overrightarrow{b} \right|\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f4eaf9cf090a16866e02da8ae1036cdb_l3.png)
The value of ![Rendered by QuickLaTeX.com \[\widehat{i}.(\widehat{j}\times \widehat{k})+\widehat{j}.(\widehat{i}\times \widehat{k})+\widehat{k}(\widehat{i}\times \widehat{j})\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-fec772ab5ec0808c89d7a1b01f17091d_l3.png)
is (A) ![Rendered by QuickLaTeX.com \[0\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b4f4fbf425b3e7b1e844d7922169d13c_l3.png)
(B) ![Rendered by QuickLaTeX.com \[-1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-644e6ba3fd2149684207ec19c2f45db3_l3.png)
(C) ![Rendered by QuickLaTeX.com \[1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-64318110f3a374fb786ef713c0b0c575_l3.png)
(D) ![Rendered by QuickLaTeX.com \[3\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-df8bcc09db12acd0f6bda88b4b8135fb_l3.png)
It is given that, Hence the correct answer is C.
Let ![Rendered by QuickLaTeX.com \[\overrightarrow{a}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f875b3d145d74fcad5c39bf1d50af3ef_l3.png)
and ![Rendered by QuickLaTeX.com \[\overrightarrow{b}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-80569b5b72a6d73d223867aa2d36880d_l3.png)
be two unit vectors and ![Rendered by QuickLaTeX.com \[\theta \]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-28c6cbc3df8e19af9d0e93bce5df4065_l3.png)
is the angle between them. Then ![Rendered by QuickLaTeX.com \[\overrightarrow{a}+\overrightarrow{b}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-47f90085f39b958a039f796aceae72d2_l3.png)
is a unit vector if (A) ![Rendered by QuickLaTeX.com \[\theta =\frac{\pi }{4}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-fc4ad60471520b848d28165e99d4ee0e_l3.png)
(B) ![Rendered by QuickLaTeX.com \[\theta =\frac{\pi }{3}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-6e401bf6731e55f12cfbb80436b54987_l3.png)
(C) ![Rendered by QuickLaTeX.com \[\theta =\frac{\pi }{2}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-024d7e0a3efe01b953a5c076a7a5c638_l3.png)
(D) ![Rendered by QuickLaTeX.com \[\theta =\frac{2\pi }{3}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-110cc2690a75e8489e60c8cab4590ada_l3.png)
![Rendered by QuickLaTeX.com \[\theta =\frac{\pi }{4}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-fc4ad60471520b848d28165e99d4ee0e_l3.png)
![Rendered by QuickLaTeX.com \[\theta =\frac{\pi }{3}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-6e401bf6731e55f12cfbb80436b54987_l3.png)
![Rendered by QuickLaTeX.com \[\theta =\frac{\pi }{2}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-024d7e0a3efe01b953a5c076a7a5c638_l3.png)
![Rendered by QuickLaTeX.com \[\theta =\frac{2\pi }{3}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-110cc2690a75e8489e60c8cab4590ada_l3.png)
Here the correct answer is option d
If ![Rendered by QuickLaTeX.com \[\theta \]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-28c6cbc3df8e19af9d0e93bce5df4065_l3.png)
is the angle between two vectors ![Rendered by QuickLaTeX.com \[\overrightarrow{a}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f875b3d145d74fcad5c39bf1d50af3ef_l3.png)
and ![Rendered by QuickLaTeX.com \[\overrightarrow{b}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-80569b5b72a6d73d223867aa2d36880d_l3.png)
, Then ![Rendered by QuickLaTeX.com \[\overrightarrow{a}.\overrightarrow{b}\ge 0\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b4dfaf184691a3ef98fcc0711022cbab_l3.png)
only when (A) ![Rendered by QuickLaTeX.com \[0<\theta <\frac{\pi }{2}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1fe8ec8f0f58a1e2bdd8049591505ed7_l3.png)
(B) ![Rendered by QuickLaTeX.com \[0\le \theta \le \frac{\pi }{2}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-6f0a816c563c90f283e9520d68aa9ae0_l3.png)
(C) ![Rendered by QuickLaTeX.com \[0<\theta <\pi \]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-db329ef216355048be6e558280aae73a_l3.png)
(D) ![Rendered by QuickLaTeX.com \[0\le \theta \le \pi \]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-6068637deeff1adbedd1def6ede23295_l3.png)
![Rendered by QuickLaTeX.com \[0<\theta <\frac{\pi }{2}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1fe8ec8f0f58a1e2bdd8049591505ed7_l3.png)
![Rendered by QuickLaTeX.com \[0\le \theta \le \frac{\pi }{2}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-6f0a816c563c90f283e9520d68aa9ae0_l3.png)
Prove that ![Rendered by QuickLaTeX.com \[(\overrightarrow{a}+\overrightarrow{b}).(\overrightarrow{a}-\overrightarrow{b})={{\left| \overrightarrow{a} \right|}^{2}}+{{\left| \overrightarrow{b} \right|}^{2}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-330d901690d8cf6234407058062682fb_l3.png)
, if and only if ![Rendered by QuickLaTeX.com \[\overrightarrow{a}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f875b3d145d74fcad5c39bf1d50af3ef_l3.png)
, ![Rendered by QuickLaTeX.com \[\overrightarrow{b}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-80569b5b72a6d73d223867aa2d36880d_l3.png)
are perpendicular, given ![Rendered by QuickLaTeX.com \[\overrightarrow{a}\ne 0,\overrightarrow{b}\ne 0\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-8b1236addf6d9c4c1412a8aa7b5efc47_l3.png)
.
![Rendered by QuickLaTeX.com \[(\overrightarrow{a}+\overrightarrow{b}).(\overrightarrow{a}-\overrightarrow{b})={{\left| \overrightarrow{a} \right|}^{2}}+{{\left| \overrightarrow{b} \right|}^{2}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-330d901690d8cf6234407058062682fb_l3.png)
It is given that Hence proved.
If ![Rendered by QuickLaTeX.com \[\overrightarrow{a}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f875b3d145d74fcad5c39bf1d50af3ef_l3.png)
, ![Rendered by QuickLaTeX.com \[\overrightarrow{b}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-80569b5b72a6d73d223867aa2d36880d_l3.png)
, ![Rendered by QuickLaTeX.com \[\overrightarrow{c}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-28e5ac2bb179eb1056bcdac7884094ee_l3.png)
. are mutually perpendicular vectors of equal magnitudes, show that the vector ![Rendered by QuickLaTeX.com \[\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-9e11e6c21752131f88e75db095b19841_l3.png)
is equally inclined to ![Rendered by QuickLaTeX.com \[\overrightarrow{a}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f875b3d145d74fcad5c39bf1d50af3ef_l3.png)
, ![Rendered by QuickLaTeX.com \[\overrightarrow{b}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-80569b5b72a6d73d223867aa2d36880d_l3.png)
and ![Rendered by QuickLaTeX.com \[\overrightarrow{c}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-28e5ac2bb179eb1056bcdac7884094ee_l3.png)
.
let us assume,
The scalar product of the vector ![Rendered by QuickLaTeX.com \[\widehat{i}+\widehat{j}+\widehat{k}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-9182cc705b62215c9f98552abb7afa12_l3.png)
with a unit vector along the sum of vectors ![Rendered by QuickLaTeX.com \[2\widehat{i}+4\widehat{j}-5\widehat{k}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a6681754ddd5c454be051d9879e7154e_l3.png)
and ![Rendered by QuickLaTeX.com \[\lambda \widehat{i}+2\widehat{j}+3\widehat{k}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a940bd8c10c3cea99b5fc268c8c30895_l3.png)
is equal to one. Find the value of ![Rendered by QuickLaTeX.com \[\lambda \]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1e5278423fe0cd24b56228ebd2dbfcd2_l3.png)
.
Let us consider
Let ![Rendered by QuickLaTeX.com \[\overrightarrow{a}=\widehat{i}+4\widehat{j}+2\widehat{k}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-edd4804415df8cbdae1204c94d7db6c6_l3.png)
, ![Rendered by QuickLaTeX.com \[\overrightarrow{b}=3\widehat{i}-2\widehat{j}+7\widehat{k}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c06b242e8db2c0dc3306d8d293afa6bc_l3.png)
and ![Rendered by QuickLaTeX.com \[\overrightarrow{c}=2\widehat{i}-\widehat{j}+4\widehat{k}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1257de77b94154648a39fbd4f389df23_l3.png)
. Find a vector ![Rendered by QuickLaTeX.com \[\overrightarrow{d}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-6e24df3bbd1902b7f7ac0f8454c6d0dd_l3.png)
which is perpendicular to both ![Rendered by QuickLaTeX.com \[\overrightarrow{a}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f875b3d145d74fcad5c39bf1d50af3ef_l3.png)
and ![Rendered by QuickLaTeX.com \[\overrightarrow{b}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-80569b5b72a6d73d223867aa2d36880d_l3.png)
, and ![Rendered by QuickLaTeX.com \[\overrightarrow{c}.\overrightarrow{d}=15\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-4672432386a0d5666406085e8fa67cc6_l3.png)
Assume,
Show that the direction cosines of a vector equally inclined to the axes OX, OY and OZ are ![Rendered by QuickLaTeX.com \[\frac{1}{\sqrt{3}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-fc27ffa7784ce20e0f96b0c1052c51c5_l3.png)
, ![Rendered by QuickLaTeX.com \[\frac{1}{\sqrt{3}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-fc27ffa7784ce20e0f96b0c1052c51c5_l3.png)
, ![Rendered by QuickLaTeX.com \[\frac{1}{\sqrt{3}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-fc27ffa7784ce20e0f96b0c1052c51c5_l3.png)
.
Firstly, Let’s assume a vector to be equally inclined to axes OX, OY, and OZ at angle \[\alpha \]. Then, the direction cosines of the vector are \[\cos \alpha \],\[\cos \alpha \]and \[\cos \alpha...
The two adjacent sides of a parallelogram are ![Rendered by QuickLaTeX.com \[2\widehat{i}-4\widehat{j}+5\widehat{k}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-4766f36f7805e520fba218aa3951172e_l3.png)
and ![Rendered by QuickLaTeX.com \[\widehat{i}-2\widehat{j}-3\widehat{k}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-9271dbf9cd7a1e0d4b6579035bdd8b97_l3.png)
. Find the unit vector parallel to its diagonal. Also, find its area.
we know that,
Find the position vector of a point R which divides the line joining two points P and Q whose position vectors are ![Rendered by QuickLaTeX.com \[(2\overrightarrow{a}+\overrightarrow{b})\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f89637921312deab284f70a94ca009eb_l3.png)
and ![Rendered by QuickLaTeX.com \[(\overrightarrow{a}-3\overrightarrow{b})\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-e04b8bab322f492b3c06c77069263be5_l3.png)
externally in the ratio ![Rendered by QuickLaTeX.com \[1:2\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-98057744c90982b103f0706671126b04_l3.png)
. Also, show that P is the midpoint of the line segment RQ.
we know that,
Show that the points A ![Rendered by QuickLaTeX.com \[(1,-2,-8)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-489c52c99a8f3fe514ef8367dd634d09_l3.png)
, B ![Rendered by QuickLaTeX.com \[(5,0,-2)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-099ce1dc50848cdaa3e15192948c9f3e_l3.png)
and C ![Rendered by QuickLaTeX.com \[(11,3,7)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-844c5d13f81314eb0793e67539dc0207_l3.png)
are collinear, and find the ratio in which B divides AC.
Let us consider
If ![Rendered by QuickLaTeX.com \[\overrightarrow{a}=\widehat{i}+\widehat{j}+\widehat{k}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-35d857b3023b451e1d87a34e4b17337b_l3.png)
, ![Rendered by QuickLaTeX.com \[\overrightarrow{b}=2\widehat{i}-\widehat{j}+3\widehat{k}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-bb09664bac6f93e8d54203ba79800eb9_l3.png)
and ![Rendered by QuickLaTeX.com \[\overrightarrow{c}=\widehat{i}-2\widehat{j}+\widehat{k}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c64e04d81b624079d16b7d4525a27c85_l3.png)
find a unit vector parallel to the vector ![Rendered by QuickLaTeX.com \[2\overrightarrow{a}-\overrightarrow{b}+3\overrightarrow{c}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1c9977111157a87f7a4a78223e574283_l3.png)
.
Let us consider
Find a vector of magnitude 5 units, and parallel to the resultant of the vectors ![Rendered by QuickLaTeX.com \[\overrightarrow{a}=2\widehat{i}+3\widehat{j}-\widehat{k}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-441cbddb8a4a7e4497122556cfb6a7b7_l3.png)
and ![Rendered by QuickLaTeX.com \[\overrightarrow{b}=\widehat{i}-2\widehat{j}+\widehat{k}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-30accd4139b3230fd0fe12fd0c6b06ae_l3.png)
let us consider,
Find the value of x for which ![Rendered by QuickLaTeX.com \[x(\widehat{i}+\widehat{j}+\widehat{k})\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-217e3c386db4107a945319020f578916_l3.png)
is a unit vector.
we know ,
If ![Rendered by QuickLaTeX.com \[\overrightarrow{a}=\overrightarrow{b}+\overrightarrow{c}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7eb9b063f3664d4111d9371d73353778_l3.png)
, then is it true that ![Rendered by QuickLaTeX.com \[\left| \overrightarrow{a} \right|=\left| \overrightarrow{b} \right|+\left| \overrightarrow{c} \right|\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-867d699a5dde3474d65f59a94fbddd72_l3.png)
? Justify your answer.
![Rendered by QuickLaTeX.com \[\left| \overrightarrow{a} \right|=\left| \overrightarrow{b} \right|+\left| \overrightarrow{c} \right|\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-867d699a5dde3474d65f59a94fbddd72_l3.png)
It is given that,
A girl walks ![Rendered by QuickLaTeX.com \[4\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3c0fa656ae249b0b1e03c8cd2e7be583_l3.png)
km towards west, then she walks ![Rendered by QuickLaTeX.com \[3\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-df8bcc09db12acd0f6bda88b4b8135fb_l3.png)
km in a direction ![Rendered by QuickLaTeX.com \[{{30}^{\circ }}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-34cd53219eaf0763feb7ca785cfc2855_l3.png)
east of north and stops. Determine the girl’s displacement from her initial point of departure.
It is given that, Let O and B be the initial and final positions of the girl respectively. Then, the girl’s position can be shown as:
. Find the scalar components and magnitude of the vector joining the points P ![Rendered by QuickLaTeX.com \[({{x}_{1}},{{y}_{1}},{{z}_{1}})\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-8e59b5607a276459e63c9744ae8cf498_l3.png)
and Q ![Rendered by QuickLaTeX.com \[({{x}_{2}},{{y}_{2}},{{z}_{2}})\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-34b4e10a50394db0a5a87bc7c7c59790_l3.png)
.
let us consider,
Write down a unit vector in XY-plane, making an angle of ![Rendered by QuickLaTeX.com \[{{30}^{\circ }}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-34cd53219eaf0763feb7ca785cfc2855_l3.png)
with the positive direction of x-axis.
let us consider,
Find the vector and the Cartesian equations of the lines that passes through the origin and (5, –2, 3).
Solution: Given: The origin $(0,0,0)$ and the point $(5,-2,3)$ It is known to us that The vector eq. of as line which passes through two points whose position vectors are $\vec{a}$ and $\vec{b}$ is...
Find the Cartesian equation of the line which passes through the point 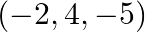 and parallel to the line given by
and parallel to the line given by 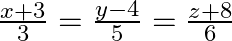
Solution: It is given that The points $(-2,4,-5)$ It is known that Now, the Cartesian equation of a line through a point $\left(\mathrm{x}_{1}, \mathrm{y}_{1}, \mathrm{z}_{1}\right)$ and having...
Find the equation of the line which passes through the point (1, 2, 3) and is parallel to the vector 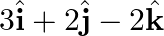
Solution: Given that, Line passes through the point $(1,2,3)$ and is parallel to the vector. It is known to us that Vector eq. of a line that passes through a given point whose position vector is...
Show that the line through the points (4, 7, 8), (2, 3, 4) is parallel to the line through the points (–1, –2, 1), (1, 2, 5).
Solution: The points $(4,7,8),(2,3,4)$ and $(-1,-2,1),(1,2,5)$. Consider $A B$ be the line joining the points, $(4,7,8),(2,3,4)$ and $C D$ be the line through the points $(-1,-2$, 1), $(1,2,5)$. So...
Show that the line through the points (1, –1, 2), (3, 4, –2) is perpendicular to the line through the points (0, 3, 2) and (3, 5, 6).
Solution: Given that The points $(1,-1,2),(3,4,-2)$ and $(0,3,2),(3,5,6)$. Let's consider $A B$ be the line joining the points, $(1,-1,2)$ and $(3,4,-2)$, and $C D$ be the line through the points...
Which of the following is a homogeneous differential equation? A. (4x + 6y + 5) dy – (3y + 2x + 4) dx = 0 B. (x y) dx – (x^3 + y^3) dy = 0 C. (x^3 + 2y^2) dx + 2xy dy = 0 D. y^2dx + (x^2 – x y – y^2) dy = 0
D. y2dx + (x2 – x y – y2) dy = 0
A homogeneous differential equation of the from 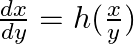 can be solved by making the substitution. (A) y = v x (B) v = y x (C) x = v y (D) x = v
can be solved by making the substitution. (A) y = v x (B) v = y x (C) x = v y (D) x = v
(C) x = v y
find the particular solution satisfying the given condition: 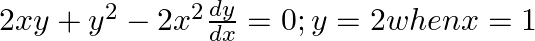
The required solution of the differential equation.
