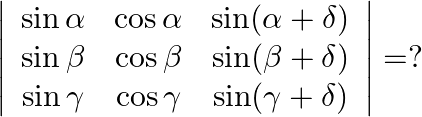Solution:
Option(A)
To find: Value of 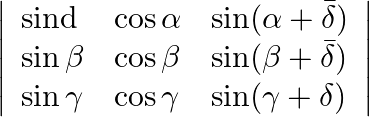
Formula Used: ![]()
We have, 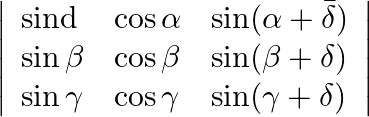
Applying ![]()
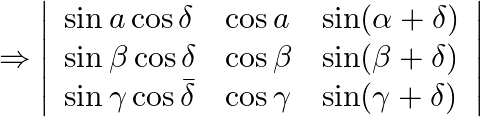
Applying ![]()
*** QuickLaTeX cannot compile formula:
\Rightarrow\left|\begin{array}{lll}
\sin a \cos \delta \overline & \cos a \sin \overline{ } & \sin (a+\bar{\delta}) \\
\sin \beta \cos \bar{\sigma} & \cos \beta \sin \bar{\sigma} & \sin (\beta+\bar{\delta}) \\
\sin \gamma \cos \delta & \cos \gamma \sin \bar{\delta} & \sin (\gamma+\bar{\delta})
\end{array}\right|
*** Error message:
Missing } inserted.
leading text: \sin a \cos \delta \overline &
Missing \cr inserted.
leading text: \sin a \cos \delta \overline &
Misplaced \cr.
leading text: \sin a \cos \delta \overline &
Missing \cr inserted.
leading text: \sin a \cos \delta \overline &
Misplaced \cr.
leading text: \sin a \cos \delta \overline &
Missing \cr inserted.
leading text: \sin a \cos \delta \overline &
Misplaced \cr.
leading text: \sin a \cos \delta \overline &
Missing \cr inserted.
leading text: \sin a \cos \delta \overline &
Misplaced \cr.
leading text: \sin a \cos \delta \overline &
Missing \cr inserted.
leading text: \sin a \cos \delta \overline &
Misplaced \cr.
leading text: \sin a \cos \delta \overline &
Missing \cr inserted.
leading text: \sin a \cos \delta \overline &
We know, ![]()
Applying ![]()
![]()
When two columns are identical then the value of determinant is 0