To find – Angle between the two pair of lines Direction ratios of L1 = (-3,-2,0) Direction ratios of L2 = (1,-3,2) Tip – If (a,b,c) be the direction ratios of the first line and (a’,b’,c’) be that...
Find the coordinates of the foot of the perpendicular drawn from the point (1, 2, 3) to the line
Find the coordinates of the foot of the perpendicular drawn from the point $(1,2,3)$ to the line $\frac{\mathrm{x}-6}{3}=\frac{\mathrm{y}-7}{2}=\frac{\mathrm{z}-7}{-2}$. Also, find the length of the...
Show that the lines and do not intersect each other.
Show that the lines $\frac{\mathrm{x}-1}{2}=\frac{\mathrm{y}+1}{3}=z$ and $\frac{\mathrm{x}+1}{5}=\frac{\mathrm{y}-2}{1}, Z=2$ do not intersect each other. Answer Given: The equations of the two...
Find the vector equation of the line passing through the point with position vector and parallel to the vector Deduce the Cartesian equations of the line.
Find the vector equation of the line passing through the point with position vector $(2 \hat{\mathrm{i}}+\hat{\mathrm{j}}-5 \hat{\mathrm{k}})$ and parallel to the vector $(\hat{i}+3...
A line passes through the point (2, 1, -3) and is parallel to the vector Find the equations of the line in vector and Cartesian forms.
A line passes through the point $(2,1,-3)$ and is parallel to the vector $(\hat{\mathrm{i}}-2 \hat{\mathrm{j}}+3 \hat{\mathrm{k}})$. Find the equations of the line in vector and Cartesian forms....
A line passes through the point (3, 4, 5) and is parallel to the vector Find the equations of the line in the vector as well as Cartesian forms.
Answer Given: line passes through point $(3,4,5)$ and is parallel to $2 \hat{\imath}+2 \hat{\jmath}-3 \hat{k}$ To find: equation of line in vector and Cartesian forms Formula Used: Equation of a...
Evaluate:
90C88 Answer : We know that: ⇒90C88=4005 Ans: ⇒90C88=4005
Evaluate:
16c13 Answer : We know that: nCr = ⇒16C13= ⇒16C13= ⇒16C13 = ⇒16C13 = ⇒16C13 = ⇒16C13 =560 Ans: 16C13=560
Evaluate:
21C4 Answer : We know that: nCr ⇒20C4 ⇒20C4 ⇒20C4 ⇒20C4 ⇒20C4 ⇒20C4 =4845 Ans: 20C4 =4845
If 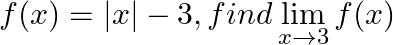
Answer:
Let 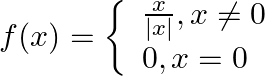 . Show that
. Show that 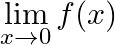 does not exist.
does not exist.
Answer:
Let 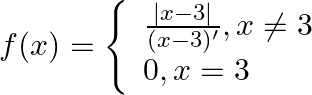 . Show that
. Show that 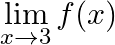 does not exist.
does not exist.
Answer:
Let 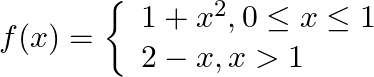 . Show that
. Show that 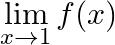 does not exist.
does not exist.
Answer:
Let 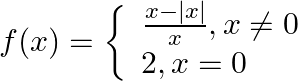 . Show that
. Show that 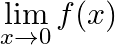 does not exist.
does not exist.
Answer:
Let 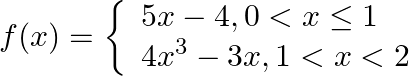 Find
Find 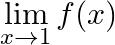
Answer:
Let 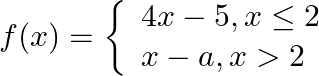 Find
Find 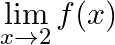
Answer:
Let 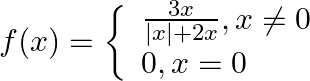 Show that
Show that 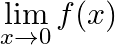 does not exist.
does not exist.
Answer:
Evaluate the following limits: 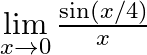
Answer:
Evaluate the following limits: 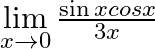
Answer:
Evaluate the following limits: 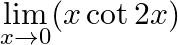
Answer:
Evaluate the following limits: 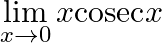
Answer:
Evaluate the following limits: 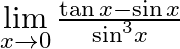
Answer:
Evaluate the following limits: 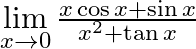
Answer:
Evaluate the following limits: 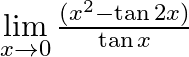
Answer:
Evaluate the following limits: 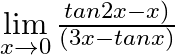
Answer:
Evaluate the following limits: 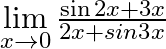
Answer:
Evaluate the following limits: 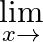 \pi
\pi 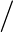 6
6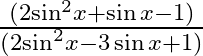
Answer:
Evaluate the following limits: 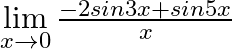
Answer:
Evaluate the following limits: 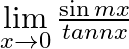
Answer:
Evaluate the following limits: 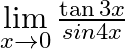
Answer:
Evaluate the following limits: 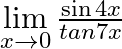
Answer:
Evaluate the following limits: 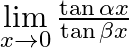
Answer:
Evaluate the following limits: 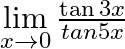
Answer:
Evaluate the following limits: 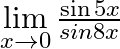
Answer:
Evaluate the following limits: 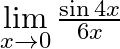
Answer:
Evaluate 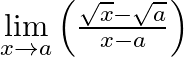
Answer:
Evaluate 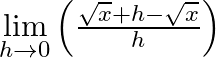
Answer:
Evaluate 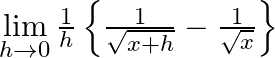
Answer:
Evaluate 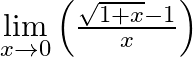
Answer:
Evaluate 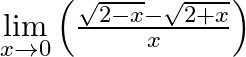
Answer:
Evaluate 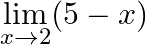
Answer:
Evaluate 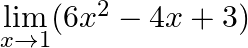
Answer:
Evaluate 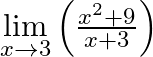
Answer:
Evaluate 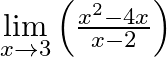
Answer:
Evaluate 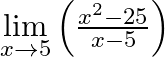
Answer:
Evaluate 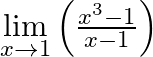
Answer:
Evaluate 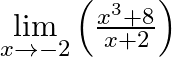
Answer:
Evaluate 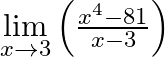
Answer:
Evaluate 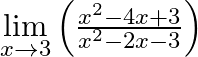
Answer:
Evaluate 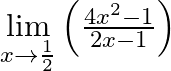
Answer:
Evaluate 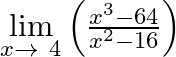
Answer:
Evaluate 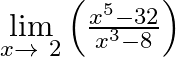
Answer:
Evaluate 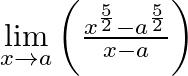
Answer:
Evaluate 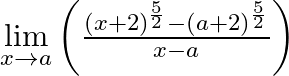
Answer:
Evaluate 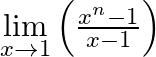
Answer:
If the mean of 5 observation x, x + 2, x + 4, x +6and x + 8 , find the value of x.
Find the sum of n terms of the series whose rth term is (r + 2^r).
Find the sum of 10 terms of the geometric series
Find the sum of the series {2^2 + 4^2 + 6^2 + …. + (2n)^2}
prove that
prove that
Find the sum 6^3 + 7^3 + 9^3 + 10^3.
Find the sum 112 + 122 + 132+ …202
Find the sum (41 + 42 + 43 + …. + 100).
Answer : It is required to find the sum (41 + 42 + 43 + …. + 100). (41 + 42 + 43 + …. + 100) = Sum of integers starting from 1 to 100 – Sum of integers starting from 1 to 40. Note: Sum of first n...
Find the sum (2 + 4 + 6 + 8 +… + 100).
Answer : It is required to find the sum of (2 + 4 + 6 + 8 +… 100).
If Sn denotes the sum of the cubes of the first n natural numbers and sn denotes the sum of the first n natural numbers then find the value of .
prove that
. Find the sum of the series: 5 + 7 + 13 + 31 + 85 + …. To n terms
Answer : In the given question we need to find the sum of the series. For that, first, we need to find the nth term of the series so that we can use summation of the series with standard...
Find the sum of the series: 1 + 5 + 12 + 22 + 35 +… to n terms
Answer : In the given question we need to find the sum of the series. For that, first, we need to find the nth term of the series so that we can use summation of the series with standard identities...
Find the sum of the series: 3 + 15 + 35 + 63 +…to n terms
Find the sum of the series:
Find the sum of the series:
Find the sum of the series:
Find the sum of the series:
Find the sum of the series: (1 × 2 × 4) + (2 × 3 × 7) + (3 × 4 × 10) + … to n terms
Find the sum of the series: (1 × 2 × 3) + (2 × 3 × 4) + (3 × 4 × 5) + … to n terms
Find the sum of the series: (3 × 12) + (5 × 22) + (7 × 32) + … to n terms
Find the sum of the series: (1 × 22) + (3 × 32) + (5 × 42) + … to n terms
Find the sum of the series: (1 × 22) + (2 × 32) + (3 × 42) + … to n terms
Find the sum of the series: (3 × 8) + (6 × 11) + (9 × 14) + … to n terms
Find the sum of the series: (1 × 2) + (2 × 3) + (3 × 4) + (4 × 5) + … to n terms
Find the sum of the series:
Find the sum of the series:
Find the sum of the series:
Find the sum of the series whose nth term is given by:
Find the sum of the series whose nth term is given by:
Find the sum of the series whose nth term is given by:
Find the sum of the series whose nth term is given by:
Find the sum of the series whose nth term is given by: n (n + 1) (n + 4)
Find the sum of the series whose nth term is given by:
Find the sum of the series whose nth term is given by:
Find the positive value of m for which the coefficient of x2 in the expansion of (1 + x)m is 6.
In the binomial expansion of (a + b)n, the coefficients of the 4th and 13thterms are equal to each other. Find the value of n.
Find the coefficient of xn in the expansion of (1 + x) (1 – x)n.
Write the 4th term from the end in the expansion of
If the coefficients of (r – 5)th and (2r – 1)th terms in the expansion of (1 + x)34 are equal, find the value of r.
Write the coefficient of x7y2 in the expansion of (x + 2y)9
Write the coefficient of the middle term in the expansion of (1 + x)2n.
Write the coefficient of the middle term in the expansion of (1 + x)2n.
Which term is independent of x in the expansion of ?
Write the number of terms in the expansion of
Show that the coefficient of x4 in the expansion of (1 + 2x + x2)5 is 212.
Prove that there is no term involving x6 in the expansion of .
Show that the coefficient of x4 in the expansion of
Show that the middle term in the expansion is 252.
Show that the coefficient of x-3 in the expansion is -330.
If the coefficients of x2 and x3 in the expansion of (3 + px)9 are the same then prove that
Show that the term independent of x in the expansion is -252.
Find the middle term in the expansion of
Prove that the coefficient of xn in the binomial expansion of (1 + x)2n is twice the coefficient of xn in the binomial expansion of (1 + x)2n-1.
Find the coefficient of x4 in the expansion of (1 + x)n (1 – x)n. Deduce that C2 = C0C4 – C1C3 + C2C2 – C3C1 + C4C0, where Cr stands for nCr.
If the 17th and 18th terms in the expansion of (2 + a)50 are equal, find the value of a.
Find the 6th term of the expansion (y1/2 + x1/3)n, if the binomial coefficient of the 3rd term from the end is 45.
If the coefficients of 2nd, 3rd and 4th terms in the expansion of (1 + x)2n are in AP, show that 2n2 – 9n + 7 = 0.
Find numerically the greatest term in the expansion of (2 + 3x)9,
Find the term independent of x in the expansion of :
Find the term independent of x in the expansion of :
Find the term independent of x in the expansion of :
Find the two middle terms in the expansion of :
Find the two middle terms in the expansion of :
Find the two middle terms in the expansion of:
Find the two middle terms in the expansion of :
Find the middle term in the expansion of :
Find the 4th term from the beginning and end in the expansion
Find the 4th term from the end in the expansion of
If the plane 2x – 3y – 6z = 13 makes an angle 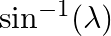 with the x-axis, then find the value of λ.
with the x-axis, then find the value of λ.
Answer: Direction ratios of the x-axis are 1,0,0 and direction ratios of normal to the plane are 2,−3,−6. The angle between the line and the plane,...
Find the vector equation of a line passing through the origin and perpendicular to the plane 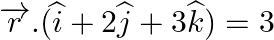
Answer:
Find the angle between the line 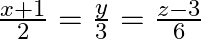 and the plane 10x + 2y – 11z = 3.
and the plane 10x + 2y – 11z = 3.
Answer: Direction ratios of the given line are 2,3,6 Direction ratios of the normal to the given plane are 10,2,−11 The angle between the line and the plane: \begin{array}{l} \sin...
Find the angle between the line 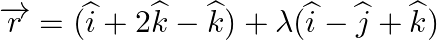 and the plane
and the plane 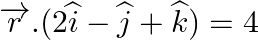
Answer: The equation of line is: $\vec{r}=(i+2 \hat{j}-\hat{k})+\lambda(\hat{i}-\hat{j}+\hat{k})$ Here, $\vec{b}=\hat{i}-j+\vec{k}$ The equation of plane is: r→·(2i^-j^+k^)=4 \vec{r}...
Find the angle between the line 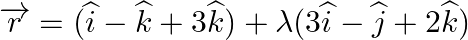 and the plane
and the plane 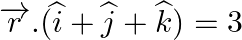
Answer: The equation of plane is: r→=(2i^-j^+3k^)+λ(3i^-j^+2k^) \vec{r}=(2 \hat{i}-\hat{j}+3 \hat{k})+\lambda(3 \hat{i}-\hat{j}+2 \hat{k}) On comparing with $\vec{r}=\vec{a}+\lambda...
Find the value of m for which the line 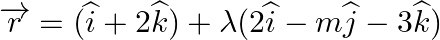 is parallel to the plane
is parallel to the plane 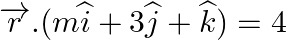
Answer: Given equation of line, $\overrightarrow r = (\widehat i + 2\widehat k) + \lambda (2\widehat i - m\widehat j - 3\widehat k)$ Comparing with the line $\overrightarrow r = \overrightarrow...
Find the angle between the line joining the points A(3,−4,−2) and B(12,2,0) and the plane 3x−y+z=1.
Answer:
Show that the line line 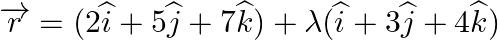 is parallel to the plane
is parallel to the plane 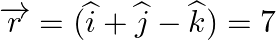 . Also, find the distance between them.
. Also, find the distance between them.
Answer: A line $\begin{array}{l} \overrightarrow r = \overrightarrow a + \lambda \overrightarrow b \\ \end{array}$ is parallel to the plane $\begin{array}{l} \overrightarrow r .\overrightarrow n ...
Find the angle between the line 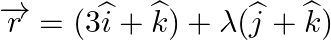 and the plane
and the plane 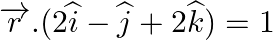
Answer: The equation of line is: r→=(3i^+k^)+λ(j^+k^) \vec{r}=(3 \hat{i}+\hat{k})+\lambda(\hat {j}+\hat{k}) Comparing with $\vec{r}=\vec{a}+\lambda \vec{b}$ $\vec{b}=(j+\dot{k})$. The...
Find the angle between the line ![Rendered by QuickLaTeX.com \[\frac{{x - 2}}{3} = \frac{{y + 1}}{{ - 1}} = \frac{{z - 3}}{{ - 2}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-24eba3255120c3288d2d203f342ddf45_l3.png)
and the plane 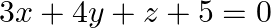
![Rendered by QuickLaTeX.com \[\frac{{x - 2}}{3} = \frac{{y + 1}}{{ - 1}} = \frac{{z - 3}}{{ - 2}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-24eba3255120c3288d2d203f342ddf45_l3.png)
Answer: The given line is $\frac{x-2}{3}=\frac{y+1}{-1}=\frac{2-3}{2}$ ⇒r→=(2i→-j→+k→)+t(3i→-j→-2k→) \Rightarrow...
Write the general term in the expansion of
Show that the expansion of does not contain any term involving x-1.
Show that the expansion of does not contain any term involving x9.
Show that the term containing x3 does not exist in the expansion
Mark the tick against the correct answer in the following: 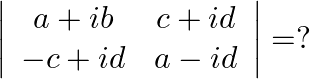
A. 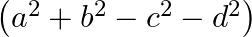
B. 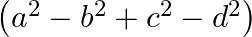
C. 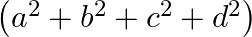
D. none of these
Solution: Option(C) To find: Value of $\left|\begin{array}{cc}a+i b & c+i d \\ -c+i d & a-i b\end{array}\right|$ Formula used: $\mathrm{i}^{2}=-1$ We have, $\left|\begin{array}{cc}a+i b...
Find the coefficient of
Mark the tick against the correct answer in the following: 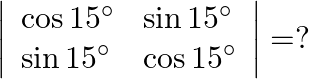
A. 1
B. 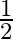
C. 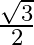
D. none of these
Solution: Option(C) To find: Value of $\left|\begin{array}{ll}\cos 15^{\circ} & \sin 15^{\circ} \\ \sin 15^{\circ} & \cos 15^{\circ}\end{array}\right|$ Formula used: (i) $\cos (A+B)=\cos A...
Find the coefficient of x in the expansion of (1 – 3x + 7×2) (1 – x)16.
Show that the ratio of the coefficient of x10 in the expansion of (1 – x2)10and the term independent of x in the expansion of is 1 : 32.
Find the ratio of the coefficient of x15 to the term independent of x in the
Find the coefficients of x7 and x8 in the expansion of .
Find the 13th term in the expansion of .
Find the 16th term in the expansion of .
Find the 9th term in the expansion of .
Find the 7th term in the expansion of .
Prove that
Using binomial theorem, prove that (23n – 7n -1) is divisible by 49, where n N.
Using binominal theorem, evaluate each of the following :
(i) (101)4
(ii) (98)4
(iii)(1.2)4
Prove that
Evaluate :
Evaluate :
Evaluate :
. Evaluate :
Using binomial theorem, expand each of the following:
Using binomial theorem, expand each of the following:
Using binomial theorem, expand each of the following:
Using binomial theorem, expand each of the following:
Using binomial theorem, expand each of the following:
Using binomial theorem, expand each of the following:
Using binomial theorem, expand each of the following:
Using binomial theorem, expand each of the following:
Using binomial theorem, expand each of the following:
Using binomial theorem, expand each of the following:
Using binomial theorem, expand each of the following:
Using binomial theorem, expand each of the following:
Find the vector and Cartesian equations of the plane passing through the origin and parallel to the vectors 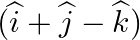 and
and 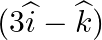 .
.
Answer:
Find the vector and Cartesian equations of the plane passing through the point (3, -1, 2) and parallel to the lines 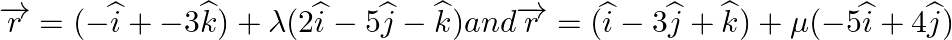 .
.
Answer:
Find the vector equation of a plane passing through the point (1, 2, 3) and parallel to the lines whose direction ratios are 1, -1, -2 and -1, 0, 2.
Answer:
Prove that the lines 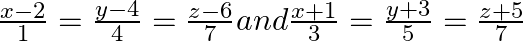 are coplanar. Also find the equation of the plane containing these lines.
are coplanar. Also find the equation of the plane containing these lines.
Answer: - 7x + 14 + 14y – 56 – 7z + 42 = 0 - 7x + 14y – 7z = 0 Multiply by negative sign, x – 2y + z = 0 The equation of...
Prove that the lines 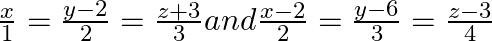 are coplanar. Also find the equation of the plane containing these lines.
are coplanar. Also find the equation of the plane containing these lines.
Answer:
Find the vector and Cartesian equations of a plane containing the two lines 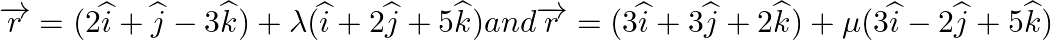 . Also show that the lines
. Also show that the lines 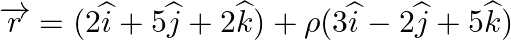 lies in the plane.
lies in the plane.
Answer: ...
Find the vector and Cartesian forms of the equations of the plane containing the two lines 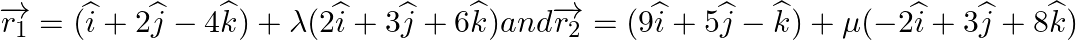 .
.
Answer:
Show that the lines 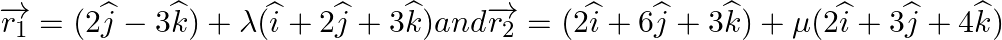 are coplanar. Also find the equation of the plane containing these lines.
are coplanar. Also find the equation of the plane containing these lines.
Answer:
Find the vector equation of a plane passing through the point (1, 2, 3) and parallel to the lines whose direction ratios are 1, -1, -2 and -1, 0, 2.
Answer:
Find the vector and Cartesian equations of the plane passing through the point (3, -1, 2) and parallel to the lines 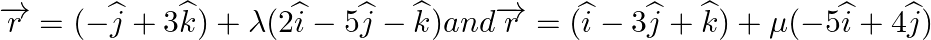
Answer:
Find the vector and Cartesian equations of the plane passing through the origin and parallel to the vectors 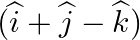 and
and 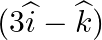 .
.
Answer:
Find the (i) lengths of the axes, (ii) coordinates of the vertices ![Rendered by QuickLaTeX.com \[\frac{{{x}^{2}}}{9}-\frac{{{y}^{2}}}{16}=1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-ad127cbd28649d4a6ca9eaa984f44acb_l3.png)
![Rendered by QuickLaTeX.com \[\frac{{{x}^{2}}}{9}-\frac{{{y}^{2}}}{16}=1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-ad127cbd28649d4a6ca9eaa984f44acb_l3.png)
Given Equation: \[\frac{{{x}^{2}}}{9}-\frac{{{y}^{2}}}{16}=1\] Comparing with the equation of hyperbola \[\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{2}}}=1\] we get, a = 3 and b = 4 (i)...
Find the acute angle between the following planes: (i) 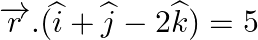 and
and 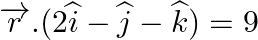 (ii)
(ii) 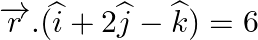 and
and 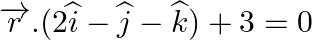 .
.
Answer: (i) (ii) ...
Find the acute angle between the following planes: (i) 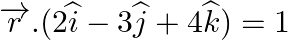 and
and 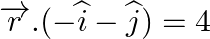 (ii)
(ii) 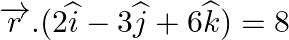 and
and 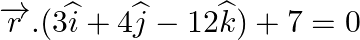 .
.
Answer: (i) (ii)
Find the value of λ for which the given planes are perpendicular to each other: (i) 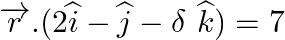 and
and 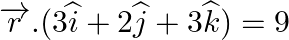 (ii)
(ii) 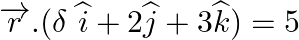 and
and 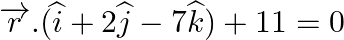 .
.
Answer: (i) For plane perpendicular, cos 900 = 0 (ii) For plane perpendicular, cos 900 = 0 (λ × 1) + (2 ×...
Show that the following planes are at right angles: (i) 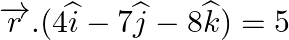 and
and 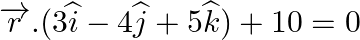 (ii)
(ii) 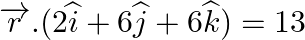 and
and 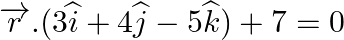 .
.
Answer: (i) (ii) = 6 + 24 – 30 = 30 – 30 = 0 = RHS Hence, the planes are...
Find the acute angle between the following planes: (i) 2x – y + z = 5 and x + y + 2z = 7 (ii) x + 2y + 2z = 3 and 2x – 3y + 6z = 8
Answer: (i) The standard equation of plane, (ii) The standard equation of plane, ...
Find the acute angle between the following planes: (i) x + y – z = 4 and x + 2y + z = 9 (ii) x + y – 2z = 6 and 2x – 2y + z = 11
Answer: (i) The standard equation of plane, (ii) The standard equation of plane, ...
Show that each of the following pairs of planes are at right angles: (i) 3x + 4y – 5z = 7 and 2x + 6y + 6z + 7 = 0 (ii) x – 2y + 4z = 10 and 18x + 17y + 4z = 49
Answer: (i) if θ = 900 then cos 900 = 0 A1A2 + B1B2 + C1C2 = 0 By comparing with the standard equation of a plane, A1 = 3, B1 = 4, C1 = -5 A2 = 2, B2 = 6, C2 = 6 LHS = A1A2 + B1B2 + C1C2 = (3 × 2) +...
Find the equation of the plane passing through the intersection of the planes x – 2y + z = 1 and 2x + y + z = 8, and parallel to the line with direction ratios 1, 2, 1. Also, find the perpendicular distance of (1, 1, 1) from the plane.
Answer: Cartesian form of equation of plane through the line of intersection of planes: ...
Find the equation of the plane passing through the line of intersection of the planes 2x – y = 0 and 3z – y = 0, and perpendicular to the plane 4x + 5y – 3z = 0.
Answer: Cartesian form of equation of plane through the line of intersection of planes: The equation...
Find the equation of the plane through the line of intersection of the planes x – 3y + z + 6 = 0 and x + 2y + 3z + 5 = 0, and passing through the origin.
Answer: Cartesian form of equation of plane through the line of intersection of planes: - x – 27y – 13z = 0 Multiplying by negative sign, x + 27y + 13z = 0 The equation of the plane is x + 27y + 13z...
Find the equation of the planes passing through the intersection of the planes 2x + 3y – z + 1 = 0 and x + y – 2z + 3 = 0, and perpendicular to the plane 3x – y – 2z – 4 = 0.
Answer: Cartesian form of equation of plane through the line of intersection of planes: The equation of the plane is 7x + 13y + 4z = 9.
Find the equation of the plane through the line of intersection of the planes x + y + z = 6 and 2x + 3y + 4z + 5 = 0, and passing through the point (1, 1, 1).
Answer: Cartesian form of equation of plane through the line of intersection of planes: 14x + 14y + 14z – 84 + 6x + 9y + 12z + 15 = 0 20x + 23y + 26z...
5. Find the equation of the plane passing through the point (1, 4, -2) and parallel to the plane 2x – y + 3z + 7 = 0.
Answer: Any plane parallel to 2x – y + 3z + 7 = 0 is shown as 2x – y + 3z + d = 0. It passes through the point (1, 4, -2) $\begin{array}{l} 2 \times 1 - 4 + 3( - 2) + d = 0\\ 2 - 4 - 6 + d = 0\\ d =...
Find the vector equation of the plane passing through the point (1, 1, 1) and parallel to the plane 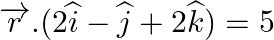 .
.
Answer:
Find the vector equation of the plane passing through the point (a, b, c) and parallel to the plane 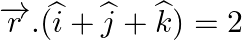 .
.
Answer:
Find the vector equation of the plane through the points 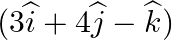 and parallel to the plane
and parallel to the plane 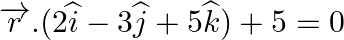 .
.
Answer:
Show that the planes 2x – y + 6z = 5 and 5x – 2.5y + 15z = 12 are parallel.
Answer:
