Solution: Option(C) To find: Area of $A B C$ Given: $A(3,-2), B(k, 2)$ and $C(8,8)$ The formula used: $\Delta=\frac{1}{2}\left|\begin{array}{lll}x_{1} & y_{1} & 1 \\ x_{2} & y_{2} &...
Mark the tick against the correct answer in the following: If the points
Mark the tick against the correct answer in the following: The solution set of the equation 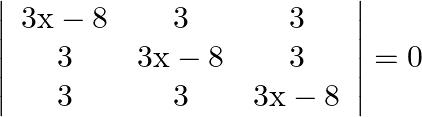 is
is
A. 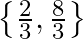
B. 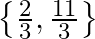
C. 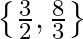
D. None of these
Solution: Option(B) To find: Value of $x$ We have, $\left|\begin{array}{ccc}3 x-8 & 3 & 3 \\ 3 & 3 x-8 & 3 \\ 3 & 3 & 3 x-8\end{array}\right|=0$ Applying $\mathrm{R}_{1}...
Mark the tick against the correct answer in the following: The solution set of the equation 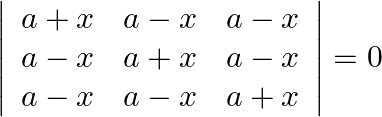 is
is
A. 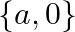
B. 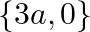
C. 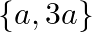
D. None of these
Solution: Option(B) To find: Value of $x$ We have, $\left|\begin{array}{ccc}a+x & a-x & a-x \\ a-x & a+x & a-x \\ a-x & a-x & a+x\end{array}\right|=0$ Applying...
Mark the tick against the correct answer in the following: The solution set of the equation 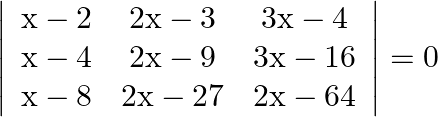 is
is
A. 
B. 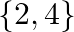
C. 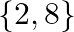
D. 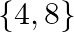
Solution: Option(A) To find: Value of $x$ We have, $\left|\begin{array}{ccc}x-2 & 2 x-3 & 3 x-4 \\ x-4 & 2 x-9 & 3 x-16 \\ x-8 & 2 x-27 & 3 x-64\end{array}\right|=0$ Applying...
Mark the tick against the correct answer in the following: If 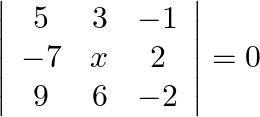 then
then 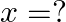
A. 0
B. 6
C. 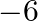
D. 9
Solution: Option(C) To find: Value of $\mathrm{x}$ We have, $\left|\begin{array}{ccc}5 & 3 & -1 \\ -7 & x & 2 \\ 9 & 6 & -2\end{array}\right|=0$ Applying $R_{1} \rightarrow 2...
Mark the tick against the correct answer in the following: 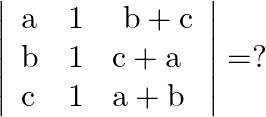
A. 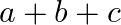
B. 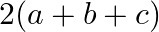
C. 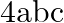
D. 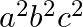
Solution: Option(C) To find: Value of $\left|\begin{array}{lll}a & 1 & b+c \\ b & 1 & c+a \\ c & 1 & a+b\end{array}\right|$ We have, $\left|\begin{array}{lll}a & 1 &...
Mark the tick against the correct answer in the following: 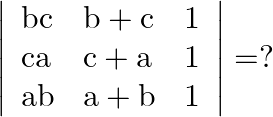
A. 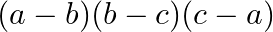
B. 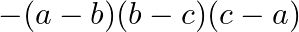
C. 
D. None of these
Solution: Option(A) To find: Value of $\left|\begin{array}{lll}\mathrm{bc} & \mathrm{b}+\mathrm{c} & 1 \\ \mathrm{ca} & \mathrm{a}+\mathrm{c} & 1 \\ \mathrm{ab} &...
Mark the tick against the correct answer in the following: 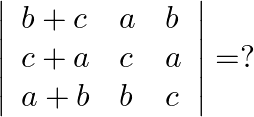
A. 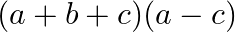
B. 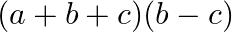
C. 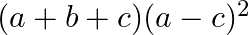
D. 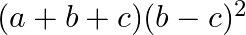
Solution: Option(C) To find: Value of $\left|\begin{array}{lll}b+c & a & b \\ c+a & c & a \\ a+b & b & c\end{array}\right|$ We have,...
Mark the tick against the correct answer in the following: 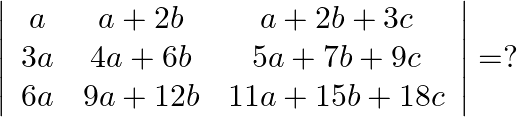
A. 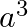
B. 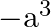
C. 0
D. none of these
Solution: Option(B) To find: Value of $\left|\begin{array}{ccc}a & a+2 b & a+2 b+3 c \\ 3 a & 4 a+6 b & 5 a+7 b+9 c \\ 6 a & 9 a+12 b & 11 a+15 b+18 c\end{array}\right|$ We...
Mark the tick against the correct answer in the following: 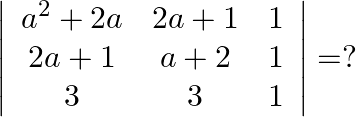
A. 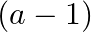
B. 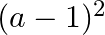
C. 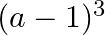
D. none of these
Solution: Option(C) To find: Value of $\left|\begin{array}{ccc}a^{2}+2 a & 2 a+1 & 1 \\ 2 a+1 & a+2 & 1 \\ 3 & 3 & 1\end{array}\right|$ We have,...
Mark the tick against the correct answer in the following: If 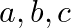 be distinct positive real numbers then the value of
be distinct positive real numbers then the value of 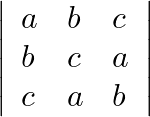 is
is
A. positive
B. negative
C. a perfect square
D. 0
Solution: Option(B) To find: Nature of $\left|\begin{array}{lll}a & b & c \\ b & c & a \\ c & a & b\end{array}\right|$ We have, $\left|\begin{array}{lll}a & b & c \\...
Mark the tick against the correct answer in the following: 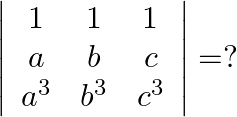
A. 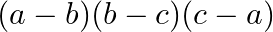
B. 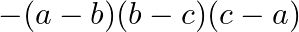
C. 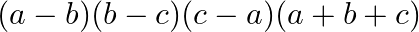
D. 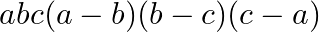
Solution: Option(C) To find: Value of $\left|\begin{array}{ccc}1 & 1 & 1 \\ a & b & c \\ a^{3} & b^{3} & c^{3}\end{array}\right|$ We have, $\left|\begin{array}{ccc}1 & 1...
Mark the tick against the correct answer in the following: 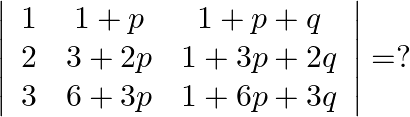
A. 0
B. 1
C. 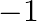
D. none of these
Solution: Option(B) To find: Value of $\left|\begin{array}{ccc}1 & 1+p & 1+p+q \\ 2 & 3+2 p & 1+3 p+2 q \\ 3 & 6+3 p & 1+6 p+3 q\end{array}\right|$ We have,...
Mark the tick against the correct answer in the following: 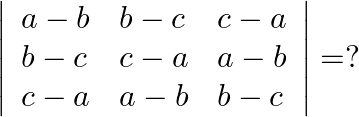
A. 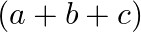
B. 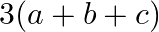
C. 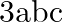
D. 0
Solution: Option(D) To find: Value of $\left|\begin{array}{lll}a-b & b-c & c-a \\ b-c & c-a & a-b \\ c-a & a-b & b-c\end{array}\right|$ We have, $\left|\begin{array}{lll}a-b...
Mark the tick against the correct answer in the following: 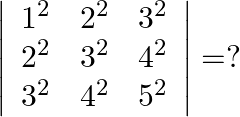
A. 8
B. 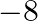
C. 16
D. 142
Solution: Option(A) To find: Value of $\left|\begin{array}{lll}1^{2} & 2^{2} & 3^{2} \\ 2^{2} & 3^{2} & 4^{2} \\ 3^{2} & 4^{2} & 5^{2}\end{array}\right|$ We have,...
Mark the tick against the correct answer in the following: If 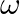 is a complex root of unity then
is a complex root of unity then 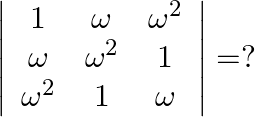
A. 1
B. 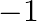
C. 0
D. none of these
Solution: Option(C) To find: Value of $\left|\begin{array}{ccc}1 & \omega & \omega^{2} \\ \omega & \omega^{2} & 1 \\ \omega^{2} & 1 & \omega\end{array}\right|$ We have,...
Mark the tick against the correct answer in the following: 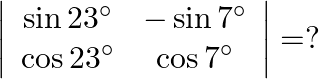
A. 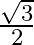
B. 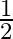
C. 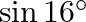
D. 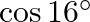
Solution: Option(B) To find: Value of $\left|\begin{array}{cc}\sin 23^{\circ} & -\sin 7^{\circ} \\ \cos 23^{\circ} & \cos 7^{\circ}\end{array}\right|$ Formula used: (i) $\sin (A+B)=\sin A...
Mark the tick against the correct answer in the following: 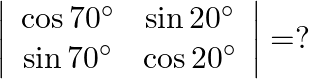
A. 1
B. 0
C. 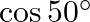
8D. 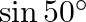
Solution: Option(B) To find: Value of $\left|\begin{array}{cc}\cos 70^{\circ} & \sin 20^{\circ} \\ \sin 70^{\circ} & \cos 20^{\circ}\end{array}\right|$ Formula used: (i) $\cos \theta=\sin...
If the points 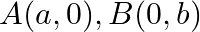 and
and 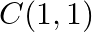 are collinear, prove that
are collinear, prove that 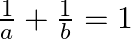
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
If 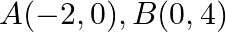 and
and 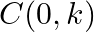 be three points such that area of a
be three points such that area of a 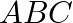 is 4 sq units, find the value of
is 4 sq units, find the value of 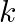 .
.
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the value of 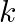 for which the area of a ABC having vertices
for which the area of a ABC having vertices 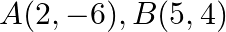 and
and 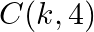 is 35 sq units.
is 35 sq units.
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the value of 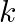 for which the points
for which the points 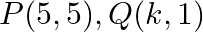 and
and 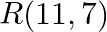 are collinear.
are collinear.
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the value of 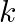 for which the points
for which the points 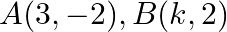 and
and 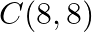 are collinear.
are collinear.
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Use determinants to show that the following points are collinear. 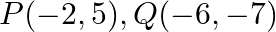 and
and 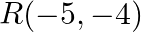
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Use determinants to show that the following points are collinear. 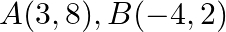 and
and 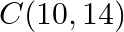
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Use determinants to show that the following points are collinear. 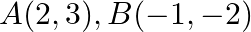 and
and 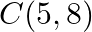
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the area of the triangle whose vertices are: 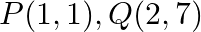 and
and 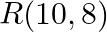
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the area of the triangle whose vertices are: 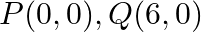 and
and 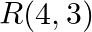
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the area of the triangle whose vertices are: 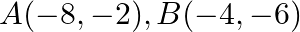 and
and 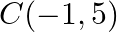
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the area of the triangle whose vertices are: 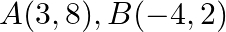 and
and 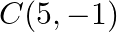
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Prove that 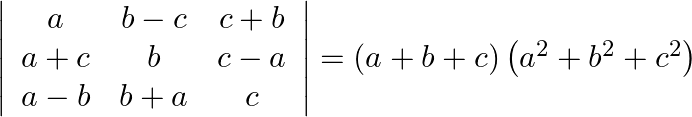
Solution: Operating $\mathrm{C}_{1} \rightarrow \mathrm{aCl}_{1}$ $=\frac{1}{a}\left|\begin{array}{ccc} a^{2} & b-c & c+b \\ a^{2}+a c & b & c-a \\ a^{2}-a b & b+a & c...
Solve the following equations: 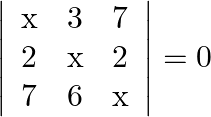
Solution: Operating $R 1 \rightarrow R 1+R_{2}+R_{3}$ $0=\left|\begin{array}{ccc} x+9 & x+9 & x+9 \\ 2 & x & 2 \\ 7 & 6 & x \end{array}\right|$ Taking $(x+9)$ common from...
Solve the following equations: 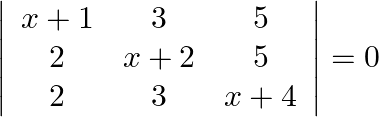
Solution: Operating $C_{1} \rightarrow C_{1}+C_{2}+C_{3}$ $0=\left|\begin{array}{ccc} x+9 & 3 & 5 \\ x+9 & x+2 & 5 \\ x+9 & 3 & x+4 \end{array}\right|$ Taking $(x+9)$ common...
Solve the following equations: 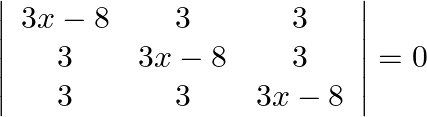
Solution: $\text { Operating } \mathrm{Cl} \rightarrow \mathrm{Cl}+\mathrm{C}_{2}+\mathrm{C}_{3}$ $0=\left|\begin{array}{ccc} 3 x-8+3+3 & 3 & 3 \\ 3+3 x-8+3 & 3 x-8 & 3 \\ 3+3+3 x-8...
Solve the following equations: 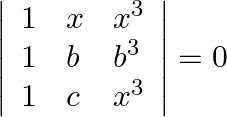
Solution: Operating $R 1 \rightarrow R 1^{-} R_{2}, R_{2 \rightarrow R 2}-R_{3}$ $\left|\begin{array}{ccc} 0 & x-b & x^{3}-b^{3} \\ 0 & b-c & b^{3}-c^{3} \\ 1 & c & c^{3}...
Show that 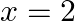 is a root of the equation
is a root of the equation 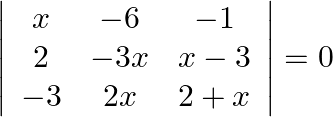 .
.
Solution: Operating $R_{1} \rightarrow R_{1}-R_{2}$ $\begin{aligned} 0 &=\left|\begin{array}{ccc} x-2 & -6+3 x & -1-x+3 \\ 2 & -3 x & x-3 \\ -3 & 2 x & 2+x...
Without expanding the determinant, prove that: 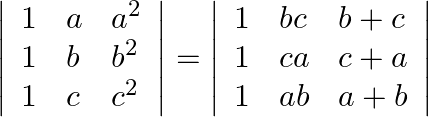
Solution: $\text { Operating } R 1 \rightarrow R 1^{-} R_{3}, R_{2 \rightarrow R_{2}-R 3}$ $\begin{array}{l} \left|\begin{array}{ccc} 0 & \mathrm{a}-\mathrm{c} &...
Without expanding the determinant, prove that: 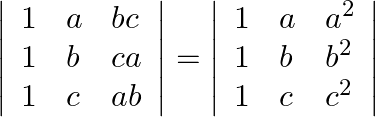
Solution: Operating $R_{1} \rightarrow R_{1}-R_{2}, R_{2} \rightarrow R_{2}-R_{3}$ $\rightarrow\left|\begin{array}{ccc} 0 & \mathrm{a}-\mathrm{b} & \mathrm{b} c-\mathrm{ac} \\ 0 &...
Prove that 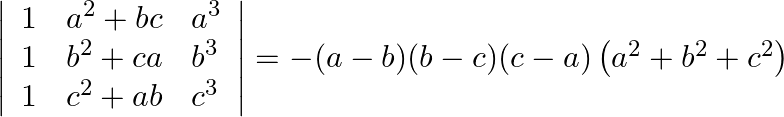
Solution: Operating $R_{1} \rightarrow R_{1}-R_{2}, R_{2} \rightarrow R_{2}-R_{3}$ $\begin{array}{l} =\left|\begin{array}{ccc} 0 & \mathrm{a}^{2}+\mathrm{bc}-\mathrm{b}^{2}-\mathrm{ac} &...
If 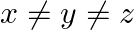 and
and 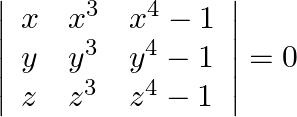 , prove that
, prove that 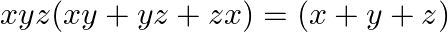
Solution: By properties of determinants, we can split the given determinant into 2 parts $\rightarrow 0=\left|\begin{array}{lll} \mathrm{x} & \mathrm{x}^{3} & \mathrm{x}^{4} \\ \mathrm{y}...
Using properties of determinants prove that: 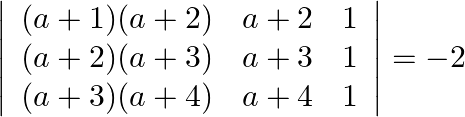
Solution: Operating $R_{1} \rightarrow R_{1}-R_{2}, R_{2} \rightarrow R_{2}-R_{3}$ $\begin{array}{l} =\left|\begin{array}{ccc} (a+1)(a+2)-(a+2)(a+3) & a+2-a-3 & 0 \\ (a+2)(a+3)-(a+3)(a+4)...
Using properties of determinants prove that: 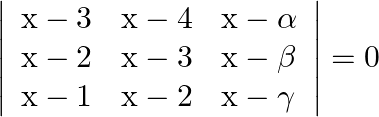 , where
, where 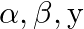 are in AP.
are in AP.
Solution: Given that $\alpha, \beta, \gamma$ are in an $A P$, which means $2 \beta=\alpha+\gamma$ Operating $R_{3} \rightarrow R_{3}-2 R_{2}+R_{1}$ $\begin{array}{l} =\left|\begin{array}{ccc} x-3...
Using properties of determinants prove that: 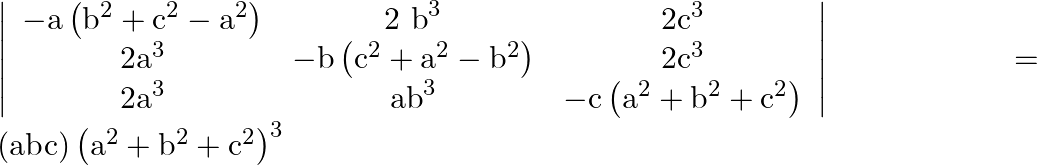
Solution: Taking $a, b, c$ from $C_{1}, C_{2}, C_{3}$ $=a b c\left|\begin{array}{ccc} -b^{2}-c^{2}+a^{2} & 2 b^{2} & 2 c^{2} \\ 2 a^{2} & b^{2}-c^{2}-a^{2} & 2 c^{2} \\ 2 a^{2} &...
Find the length of tangent drawn to a circle with radius 8 cm form a point 17 cm away from the center of the circle
Using properties of determinants prove that: 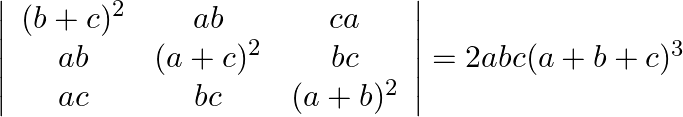
Solution: $=\left|\begin{array}{ccc} b^{2}+c^{2}+2 b c & a b & a c \\ a b & a^{2}+c^{2}+2 a c & b c \\ a c & b c & a^{2}+b^{2}+2 a b \end{array}\right|$ Operating $R_{1}...
Using properties of determinants prove that: 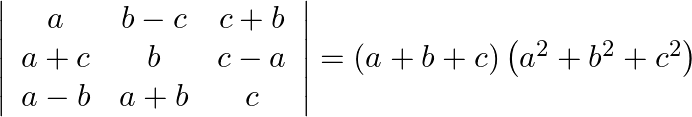
Solution: Operating $\mathrm{C}_{1} \rightarrow \mathrm{aCl}_{1}$ $\frac{1}{a}\left|\begin{array}{ccc} a^{2} & b-c & c+b \\ a^{2}+a c & b & c-a \\ a^{2}-a b & a+b & c...
Using properties of determinants prove that: 
Solution: Operating $R_{1} \rightarrow R_{1}+b R_{3}, R_{2} \rightarrow R_{2^{-}} a R_{3}$ $\begin{array}{l} \left|\begin{array}{ccc} 1+a^{2}-b^{2}+2 b^{2} & 2 a b-2 a b & -2 b+b-a^{2}...
Using properties of determinants prove that: 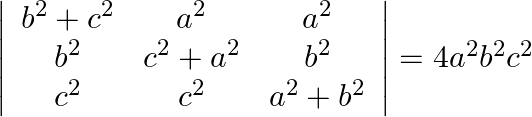
Solution: $\begin{array}{l} \left|\begin{array}{ccc} b^{2}+c^{2} & a^{2} & a^{2} \\ b^{2} & c^{2}+a^{2} & b^{2} \\ c^{2} & c^{2} & a^{2}+b^{2} \end{array}\right| \\...
Using properties of determinants prove that: 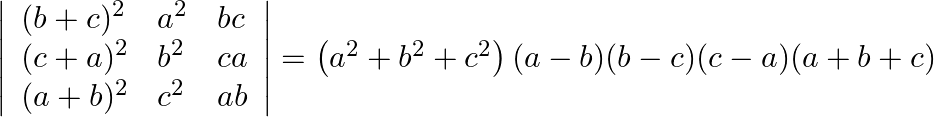
Solution: $\begin{array}{l} \left|\begin{array}{lll} (b+c)^{2} & a^{2} & b c \\ (c+a)^{2} & b^{2} & c a \\ (a+b)^{2} & c^{2} & a b \end{array}\right| \\...
Using properties of determinants prove that: 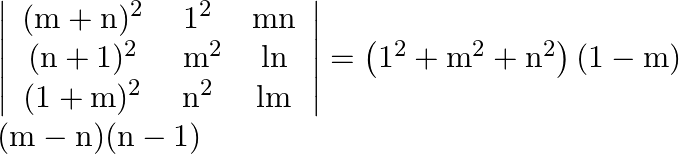
Solution: $\left|\begin{array}{ccc}(\mathrm{m}+\mathrm{n})^{2} & \mathrm{l}^{2} & \mathrm{mn} \\ (\mathrm{n}+\mathrm{l})^{2} & \mathrm{~m}^{2} & \mathrm{ln} \\ (1+\mathrm{m})^{2}...
Using properties of determinants prove that: 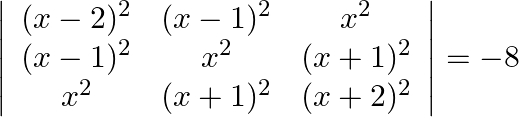
Solution: $\begin{array}{l} \left|\begin{array}{ccc} (\mathrm{x}-2)^{2} & (\mathrm{x}-1)^{2} & \mathrm{x}^{2} \\ (\mathrm{x}-1)^{2} & \mathrm{x}^{2} & (\mathrm{x}+1)^{2} \\...
Using properties of determinants prove that: 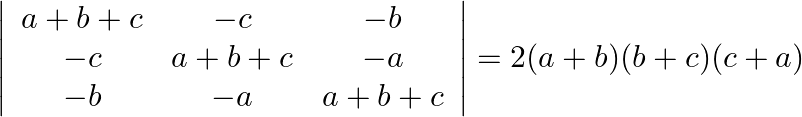
Solution: $\begin{array}{l} \left|\begin{array}{ccc} a+b+c & -c & -b \\ -c & a+b+c & -a \\ -b & -a & a+b+c \end{array}\right| \\ =\left|\begin{array}{ccc} a+b & a+b &...
Using properties of determinants prove that: 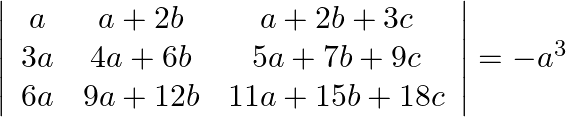
Solution: $\left|\begin{array}{ccc}a & a+2 b & a+2 b+3 c \\ 3 a & 4 a+6 b & 5 a+7 b+9 c \\ 6 a & 9 a+12 b & 11 a+15 b+18 c\end{array}\right|$...
Using properties of determinants prove that: 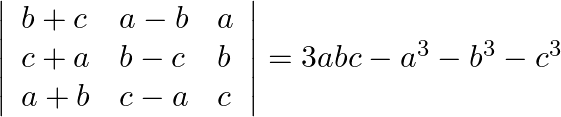
Solution: $\begin{array}{l} \left|\begin{array}{lll} \mathrm{b}+\mathrm{c} & \mathrm{a}-\mathrm{b} & \mathrm{a} \\ \mathrm{c}+\mathrm{a} & \mathrm{b}-\mathrm{c} & \mathrm{b} \\...
Using properties of determinants prove that: 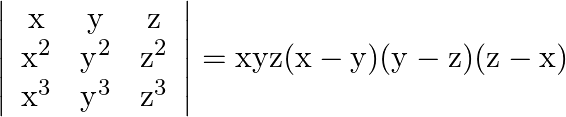
Solution: $\begin{array}{l} \left|\begin{array}{ccc} \mathrm{x} & \mathrm{y} & \mathrm{z} \\ \mathrm{x}^{2} & \mathrm{y}^{2} & \mathrm{z}^{2} \\ \mathrm{x}^{3} & \mathrm{y}^{3}...
Using properties of determinants prove that: 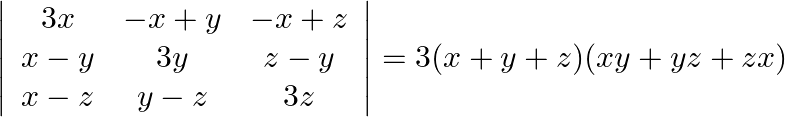
Solution: $\begin{array}{l} \left|\begin{array}{ccc} 3 x & -x+y & -x+z \\ x-y & 3 y & z-y \\ x-z & y-z & 3 z \end{array}\right| \\ =\left|\begin{array}{ccc} x+y+z & -x+y...
Using properties of determinants prove that: 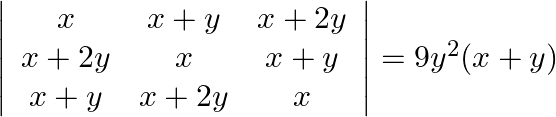
Solution: $\begin{array}{l} \left|\begin{array}{ccc} \mathrm{x} & \mathrm{x}+\mathrm{y} & \mathrm{x}+2 \mathrm{y} \\ \mathrm{x}+2 \mathrm{y} & \mathrm{x} & \mathrm{x}+\mathrm{y} \\...
Using properties of determinants prove that: 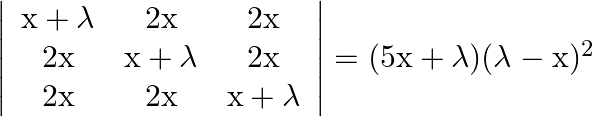
Solution: $\begin{array}{l} \left|\begin{array}{ccc} \mathrm{x}+\lambda & 2 \mathrm{x} & 2 \mathrm{x} \\ 2 \mathrm{x} & \mathrm{x}+\lambda & 2 \mathrm{x} \\ 2 \mathrm{x} & 2...
Using properties of determinants prove that: 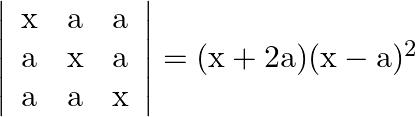
Solution: $\begin{array}{l} \left|\begin{array}{lll} \mathrm{x} & \mathrm{a} & \mathrm{a} \\ \mathrm{a} & \mathrm{x} & \mathrm{a} \\ \mathrm{a} & \mathrm{a} & \mathrm{x}...
Using properties of determinants prove that: 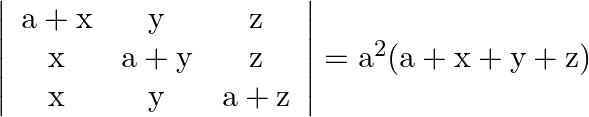
Solution: $\begin{array}{l} \left|\begin{array}{ccc} \mathrm{a}+\mathrm{x} & \mathrm{y} & \mathrm{z} \\ \mathrm{x} & \mathrm{a}+\mathrm{y} & \mathrm{z} \\ \mathrm{x} & \mathrm{y}...
Using properties of determinants prove that: 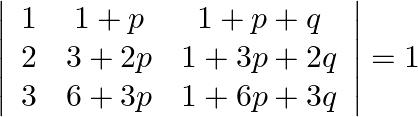
Solution: $\begin{array}{l} \left|\begin{array}{ccc} 1 & 1+p & 1+p+q \\ 2 & 3+2 p & 1+3 p+2 q \\ 3 & 6+3 p & 1+6 p+3 q \end{array}\right|\\ =\left|\begin{array}{ccc} -1 &...
Using properties of determinants prove that: 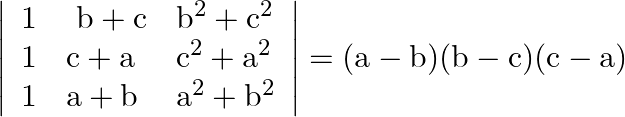
Solution: $\begin{array}{l} \left|\begin{array}{llll} 1 & \mathrm{~b}+\mathrm{c} & \mathrm{b}^{2}+\mathrm{c}^{2} \\ 1 & \mathrm{c}+\mathrm{a} & \mathrm{c}^{2}+\mathrm{a}^{2} \\ 1...
Using properties of determinants prove that: 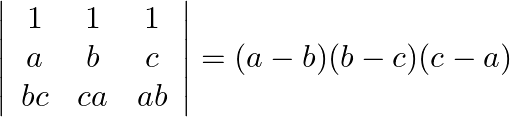
Solution: $\begin{array}{l} \left|\begin{array}{ccc} 1 & 1 & 1 \\ a & b & c \\ b c & c a & a b \end{array}\right| \\ =\left|\begin{array}{ccc} 0 & 0 & 1 \\ a-b &...
Evaluate : 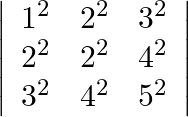
Solution: $\left|\begin{array}{lll} 1^{2} & 2^{2} & 3^{2} \\ 2^{2} & 3^{2} & 4^{2} \\ 3^{2} & 4^{2} & 5^{2} \end{array}\right|=\left|\begin{array}{ccc} 1 & 4 & 9 \\ 4...
Evaluate : 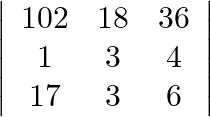
Solution: $\left|\begin{array}{ccc} 102 & 18 & 36 \\ 1 & 3 & 4 \\ 17 & 3 & 6 \end{array}\right|=6 \times\left|\begin{array}{ccc} 17 & 18 & 6 \\ 1 & 6 & 4 \\...
Evaluate: 
Solution: $\left|\begin{array}{lll}29 & 26 & 22 \\ 25 & 31 & 27 \\ 63 & 54 & 46\end{array}\right|$ $=\left|\begin{array}{ccc}4 & -5 & -5 \\ 25 & 31 & 27 \\ 63...
Evaluate 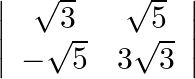
Solution: $\left|\begin{array}{cc}\sqrt{3} & \sqrt{5} \\ -\sqrt{5} & 3 \sqrt{3}\end{array}\right| \cdot=3 \sqrt{3} \times \sqrt{3}-(-\sqrt{5} \times \sqrt{5})$ $=14$
For what value of  , the given matrix
, the given matrix ![Rendered by QuickLaTeX.com A=\left[\begin{array}{cc}3-2 x & x+1 \\ 2 & 4\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-6d1f81dc4f5441083b9e76c825f8968a_l3.png) is a singular matrix?
is a singular matrix?
Solution: For $A$ to be singular matrix its determinant should be equal to 0 . $\begin{array}{l} 0=(3-2 x) \times 4-(x+1) \times 2 \\ 0=12-8 x-2 x-2 \\ 0=10-10 x \\ x=1 \end{array}$
Without expanding the determinant, prove that 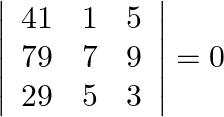 . SINGULAR MATRIX A square matrix
. SINGULAR MATRIX A square matrix  is said to be singular if
is said to be singular if 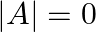 . Also,
. Also,  is called non singular if
is called non singular if 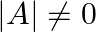 .
.
Solution: We know that $C_{1} \Rightarrow C_{1}-C_{2}$, would not change anything for the determinant. Applying the same in above determinant, we get $\left[\begin{array}{lll}40 & 1 & 5 \\...
Evaluate 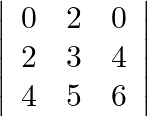
Solution: We know that expansion of determinant with respect to first row is $a_{11} A_{11}+a_{12} A_{12}+a_{13} A_{13}$. $0(3 \times 6-5 \times 4)-2(2 \times 6-4 \times 4)+0(2 \times 5-4 \times 3)$...
Evaluate 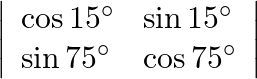
Solution: $\begin{array}{l} \cos 15^{\circ} \cos 75^{\circ}-\sin 75^{\circ} \sin 15^{\circ} \\ =\cos \left(15^{\circ}+75^{\circ}\right) \because \cos A \cos B-\sin A \sin B=\cos (A+B) \\ =\cos...
Evaluate 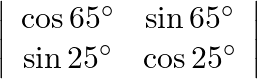
Solution: By directly opening this determinant $\begin{array}{l} \cos 65^{\circ} \times \cos 25^{\circ}-\sin 25^{\circ} \times \sin 65^{\circ} \\ =\cos \left(65^{\circ}+25^{\circ}\right) \because...
Evaluate 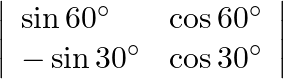
Solution: After finding determinant we will get, $\begin{array}{l} \operatorname{Sin} 60^{\circ}=\frac{\sqrt{3}}{2}=\cos 30^{\circ} \\ \operatorname{Cos} 60^{\circ}=\frac{1}{2}=\sin 30^{\circ} \\...
Evaluate 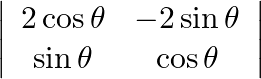
Solution: After finding determinant we will get a trigonometric identity. $\begin{array}{l} 2 \cos ^{2} \theta+2 \sin ^{2} \theta \\ =2 \\ \because \sin ^{2} \theta+\cos ^{2} \theta=1...
Evaluate 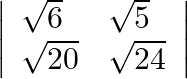 .
.
Solution: Find determinant $\begin{array}{l} \sqrt{6} \times \sqrt{24-\sqrt{2}} 20 \times \sqrt{5} \\ \sqrt{1} 144-\sqrt{1} 100 \\ =12-10 \\ =2 \end{array}$
If ![Rendered by QuickLaTeX.com \mathrm{A}=\left[\begin{array}{ll}3 & 4 \\ 1 & 2\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-9332ef694cc023ffd6fab878ba6dae64_l3.png) , find the value of
, find the value of 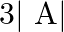 .
.
Solution: Find the determinant of $A$ and then multiply it by 3 $\begin{array}{l} |A|=2 \\ 3|A|=3 \times 2 \\ =6 \end{array}$
If 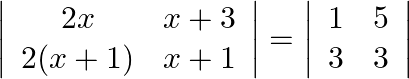 , write the value of
, write the value of  .
.
Solution: Simply by equating both sides we can get the value of $x$. $\begin{array}{l} 2 x^{2}+2 x-2\left(x^{2}+4 x+3\right)=-12 \\ \Rightarrow-6 x-6=-12 \\ \Rightarrow-6 x=-6 \\ \Rightarrow x=1...
If 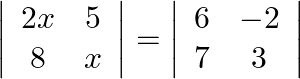 , write the value of
, write the value of  .
.
Solution: This question is having the same logic as above. $\begin{array}{l} 2 x^{2}-40=18+14 \\ \Rightarrow 2 x^{2}=72 \\ \Rightarrow x^{2}=36 \\ \Rightarrow x=\pm 6 \end{array}$
If 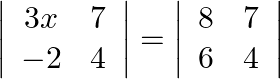 , write the value of
, write the value of  .
.
Solution: Here the determinant is compared so we need to take determinant both sides then find $\mathrm{x}$. $\begin{array}{l} 12 x+14=32-42 \\ \Rightarrow 12 x=-10-14 \\ \Rightarrow 12 x=-24 \\...
Evaluate 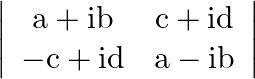
Solution: This we can very simply go through directly. $\begin{array}{l} ((a+i b)(a-i b))-((-c+i d)(c+i d)) \\ \Rightarrow\left(a^{2}+b^{2}\right)-\left(-c^{2}-d^{2}\right) \\ \Rightarrow...
Evaluate 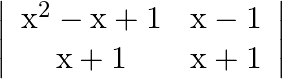
Solution: Theorem: This evaluation can be done in two different ways either by taking out the common things anc then calculating the determinants or simply take determinant. I will prefer first...
Let 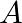 be a square matrix of order 3, write the value of
be a square matrix of order 3, write the value of 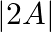 , where
, where 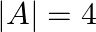 .
.
Solution: Theorem: If $A$ be $k \times k$ matrix then $|p A|=p^{k}|A|$. Given: $p=2, k=3$ and $|A|=4$ $\begin{array}{l} |2 A|=2^{3} \times|A| \\ =8 \times 4 \\ =32 \end{array}$
If 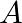 is a
is a  matrix such that
matrix such that 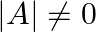 and
and 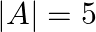 , write the value of
, write the value of 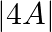 .
.
Solution: Theorem: If $A$ be $k \times k$ matrix then $|p A|=p^{k}|A|$. Given, $\mathrm{p}=4, \mathrm{k}=2$ and $|\mathrm{A}|=5$. $\begin{array}{l} |4 \mathrm{~A}|=4^{2} \times 5 \\ =16 \times 5 \\...
Mark the tick against the correct answer in the following: Domain of 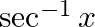 is
is
A. ![Rendered by QuickLaTeX.com [-1,1]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-bd9ec9b7fdf72f6f954becf26cf7129a_l3.png)
B. 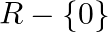
C. ![Rendered by QuickLaTeX.com R-[-1,1]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-50e13964a43d48d7f1dc0a8ed805a5fa_l3.png)
D. 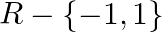
Solution: Option(C) is correct. To Find: The Domain of $\sec ^{-1}(x)$ Here,the inverse function is given by $y=f^{-1}(x)$ The graph of the function $y=\sec ^{-1}(x)$ can be obtained from the graph...
Mark the tick against the correct answer in the following: Domain of 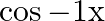 is
is
A. ![Rendered by QuickLaTeX.com [0,1]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a172ffb7f81d132bb8f882837e234a51_l3.png)
B. ![Rendered by QuickLaTeX.com [-1,1]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-bd9ec9b7fdf72f6f954becf26cf7129a_l3.png)
C. ![Rendered by QuickLaTeX.com [-1,0]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-8752afe84dfa40e1f5916867a3991fed_l3.png)
D. None of these
Solution: Option(B) is correct. To Find: The Domain of $\cos ^{-1}(x)$ Here,the inverse function of $\cos$ is given by $y=f^{-1}(x)$ The graph of the function $y=\cos ^{-1}(x)$ can be obtained from...
Mark the tick against the correct answer in the following: Range of 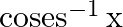 is
is
A. 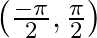
B. ![Rendered by QuickLaTeX.com \left[\frac{-\pi}{2}, \frac{\pi}{2}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d03f7933dddf8dbceee8c92c85707a25_l3.png)
C. ![Rendered by QuickLaTeX.com \left[\frac{-\pi}{2}, \frac{\pi}{2}\right]-\{0\}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c1b4b19d92f0ad0d4cedf9d79013a65d_l3.png)
D. None of these
Solution: Option(C) is correct. To Find: The range of $\operatorname{cosec}^{-1}(x)$ Here,the inverse function is given by $\mathrm{y}=\mathrm{f}^{-1}(x)$ The graph of the function...
Mark the tick against the correct answer in the following: Range of 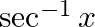 is
is
A. ![Rendered by QuickLaTeX.com \left[0, \frac{\pi}{2}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-cdf7f72b896a3c8ef3745557ca17a3c9_l3.png)
B. ![Rendered by QuickLaTeX.com [0, \pi]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3ee8a7f2b7324e2152a4807a1b912cfc_l3.png)
C. ![Rendered by QuickLaTeX.com [0, \pi]-\left\{\frac{\pi}{2}\right\}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c7ddbce50a6e98fb8f2a1854735e3fac_l3.png)
D. None of these
Solution: Option(C) is correct. To Find:The range of $\sec ^{-1}(x)$ Here,the inverse function is given by $y=f^{-1}(x)$ The graph of the function $y=\sec ^{-1}(x)$ can be obtained from the graph of...
Mark the tick against the correct answer in the following: Range of 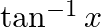 is
is
A. 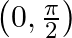
B. 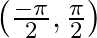
C. ![Rendered by QuickLaTeX.com \left[\frac{\pi}{2}, \frac{\pi}{2}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-ed1b0c0afbc8394951aac5d699c6de92_l3.png)
D. None of these
Solution: Option(B) is correct. To Find: The range of $\tan ^{-1} x$ Here, the inverse function is given by $y=f^{-1}(x)$ The graph of the function $y=\tan ^{-1}(x)$ can be obtained from the graph...
Mark the tick against the correct answer in the following: Range of 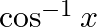 is
is
A. ![Rendered by QuickLaTeX.com [0, \pi]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3ee8a7f2b7324e2152a4807a1b912cfc_l3.png)
B. ![Rendered by QuickLaTeX.com \left[0, \frac{\pi}{2}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-cdf7f72b896a3c8ef3745557ca17a3c9_l3.png)
C. ![Rendered by QuickLaTeX.com \left[\frac{-\pi}{2}, \frac{\pi}{2}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d03f7933dddf8dbceee8c92c85707a25_l3.png)
D. None of these
Solution: Option(A) is correct. To Find: The range of $\cos ^{-1} x$ Here, the inverse function is given by $\mathrm{y}=\mathrm{f}^{-1}(x)$ The graph of the function $y=\cos ^{-1}(x)$ can be...
Mark the tick against the correct answer in the following: Range of 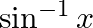 is
is
A. ![Rendered by QuickLaTeX.com \left[0, \frac{\pi}{2}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-cdf7f72b896a3c8ef3745557ca17a3c9_l3.png)
B. ![Rendered by QuickLaTeX.com [0, \pi]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3ee8a7f2b7324e2152a4807a1b912cfc_l3.png)
C. ![Rendered by QuickLaTeX.com \left[\frac{-\pi}{2}, \frac{\pi}{2}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d03f7933dddf8dbceee8c92c85707a25_l3.png)
D. None of these
Solution: Option() is correct. To Find: The range of $\sin ^{-1} x$ Here,the inverse function is given by $\mathrm{y}=\mathrm{f}^{-1}(x)$ The graph of the function $y=\sin ^{-1}(x)$ can be obtained...
Mark the tick against the correct answer in the following: 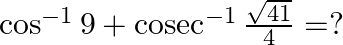
A. 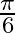
B. 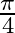
C. 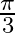
D. 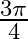
Solution: Option(B) is correct. To Find: The value of $\cot ^{-1} 9+\operatorname{cosec}^{-1} \frac{\sqrt{41}}{4}$ Now $\cot ^{-1} 9+\operatorname{cosec}^{-1} \frac{\sqrt{41}}{4}$ can be written in...
Mark the tick against the correct answer in the following: 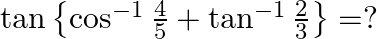
A. 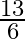
B. 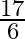
C. 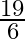
D. 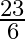
Solution: Option(B) is correct. To Find: The value of $\tan \left\{\cos ^{-1} \frac{4}{5}+\tan ^{-1} \frac{2}{3}\right\}$ Let $x=\cos ^{-1} \frac{4}{5}$ $\Rightarrow \cos x=\frac{4}{5}=\frac{\text {...
Mark the tick against the correct answer in the following: If 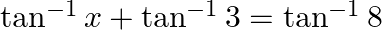 then
then 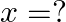
A. 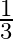
B. 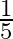
C. 3
D. 5
Solution: Option(B) is correct. Given: $\tan ^{-1} x+\tan ^{-1} 3=\tan ^{-1} 8$ To Find: The value of $x$ Here $\tan ^{-1} x+\tan ^{-1} 3=\tan ^{-1} 8$ can be written as $\tan ^{-1} x=\tan ^{-1}...
If 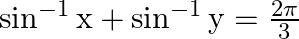 then
then 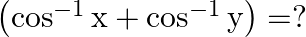
A. 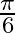
B. 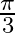
C. 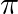
D. 
Solution: Option(B) is correct. Given: $\sin ^{-1} x+\sin ^{-1} y=\frac{2 \pi}{3}$ To Find: The value of $\cos ^{-1} x+\cos ^{-1} y$ Since we know that $\sin ^{-1} x+\cos ^{-1} x=\frac{\pi}{2}$...
Mark the tick against the correct answer in the following: If 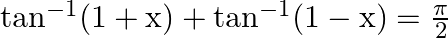 then
then 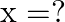
A. 1
B. 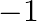
C. 0
D. 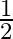
Solution: Option(C) is correct. To Find: The value of $\tan ^{-1}(1+x)+\tan ^{-1}(1-x)=\frac{\pi}{2}$ Since we know that $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$...
Mark the tick against the correct answer in the following: If 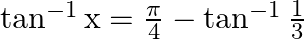 then
then 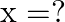
A. 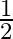
B. 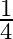
C. 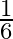
D. None of these
Solution: Option(A) is correct. To Find: The value of $\tan ^{-1} x=\frac{\pi}{4}-\tan ^{-1} \frac{1}{3}$ Now, $\tan ^{-1} x=\tan ^{-1} 1-\tan ^{-1} \frac{1}{3}\left(\because \tan...
Mark the tick against the correct answer in the following: ![Rendered by QuickLaTeX.com \sin \left[2 \tan ^{-1} \frac{5}{8}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-111a4736820b38750893122ca95b27ed_l3.png)
A. 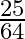
B. 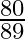
C. 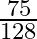
D. none of these
Solution: Option(B) is correct. To Find: The value of $\sin \left(2 \tan ^{-1} \frac{5}{8}\right)$ Let, $x=\sin \left(2 \tan ^{-1} \frac{5}{8}\right)$ We know that $2 \tan ^{-1} x=\sin...
Mark the tick against the correct answer in the following: 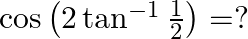
A. 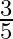
B. 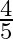
C. 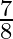
D. none of these
Solution: Option(A) is correct. To Find: The value of $\cos \left(2 \tan ^{-1} \frac{1}{2}\right)$ Let, $x=\cos \left(2 \tan ^{-1} \frac{1}{2}\right)$ $\Rightarrow \mathrm{x}=\cos \left(\tan ^{-1}...
Mark the tick against the correct answer in the following: 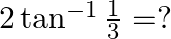
A. 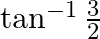
B. 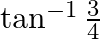
C. 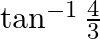
D. none of these
Solution: Option(B) is correct. To Find: The value of $2 \tan ^{-1} \frac{1}{3}$ i.e, $\tan ^{-1} \frac{1}{3}+\tan ^{-1} \frac{1}{3}$ Let, $x=\tan ^{-1} \frac{1}{3}+\tan ^{-1} \frac{1}{3}$ Since we...
Mark the tick against the correct answer in the following: 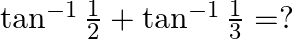
A. 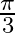
B. 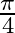
C. 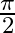
D. 
Solution: Option(B) is correct. To Find: The value of $\tan ^{-1} \frac{1}{2}+\tan ^{-1} \frac{1}{3}$ Let, $x=\tan ^{-1} \frac{1}{2}+\tan ^{-1} \frac{1}{3}$ Since we know that $\tan ^{-1} x+\tan...
Mark the tick against the correct answer in the following: 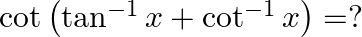
A. 1
B. 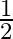
C. 0
D. none of these
Solution: Option(C) is correct. To Find: The value of $\cot \left(\tan ^{-1} x+\cot ^{-1} x\right)$ Let, $x=\cot \left(\tan ^{-1} x+\cot ^{-1} x\right)$ $\begin{array}{l} \Rightarrow \mathrm{x}=\cot...
Mark the tick against the correct answer in the following: 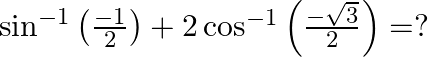
A. 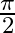
B. 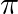
C. 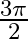
D. none of these
Solution: Option(C) is correct. To Find: The value of $\sin ^{-1}\left(\frac{-1}{2}\right)+2 \cos ^{-1}\left(\frac{-\sqrt{3}}{2}\right)$ Let, $x=\sin ^{-1}\left(\frac{-1}{2}\right)+2 \cos...
Mark the tick against the correct answer in the following: If 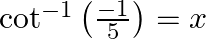 then
then 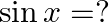
A. 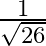
B. 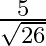
C. 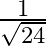
D. none of these
Solution: Option(B) is correct. Given: $\cot ^{-1} \frac{-1}{5}=x$ To Find: The value of $\sin \mathrm{x}$ Since, $x=\cot ^{-1} \frac{-1}{5}$ $\Rightarrow \cot \mathrm{x}=\frac{-1}{5}=\frac{\text {...
Mark the tick against the correct answer in the following: 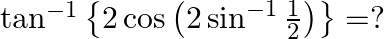
A. 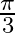
B. 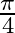
C. 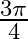
D. 
Solution: Option(B) is correct. To Find: The value of $\tan ^{-1}\left\{2 \cos \left(2 \sin ^{-1} \frac{1}{2}\right)\right\}$ Let, $x=\tan ^{-1}\left\{2 \cos \left(2 \sin ^{-1}...
Mark the tick against the correct answer in the following: 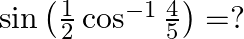
A. 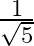
B. 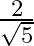
C. 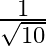
D. 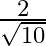
Solution: Option(C) is correct. To Find: The value of $\sin \left(\frac{1}{2} \cos ^{-1} \frac{4}{5}\right)$ Let $x=\cos ^{-1} \frac{4}{5}$ $\Rightarrow \cos x=\frac{4}{5}$ Therefore $\sin...
Mark the tick against the correct answer in the following: 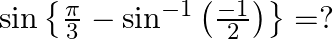
A. 1
B. 0
C. 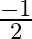
D. none of these
Solution: Option(A) is correct. To Find: The value of of $\sin \left\{\frac{\pi}{3}-\sin ^{-1}\left(\frac{-1}{2}\right)\right\}$ Let, $x=\sin \left\{\frac{\pi}{3}-\sin...
Mark the tick against the correct answer in the following: 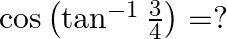
A. 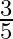
B. 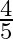
C. 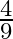
D. none of these
Solution: Option(B) is correct. To Find: The value of $\cos \left(\tan ^{-1} \frac{3}{4}\right)$ Let $x=\tan ^{-1} \frac{3}{4}$ $\begin{array}{l} \Rightarrow \tan x=\frac{3}{4} \\ \Rightarrow \tan...
Mark the tick against the correct answer in the following: 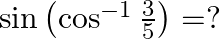
A. 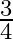
B. 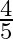
C. 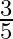
D. none of these
Solution: Option(B) is correct. To Find: The value of $\sin \left(\cos ^{-1} \frac{3}{5}\right)$ Let, $x=\cos ^{-1} \frac{3}{5}$ $\Rightarrow \cos x=\frac{3}{5}$ Now, $\sin \left(\cos ^{-1}...
Mark the tick against the correct answer in the following: 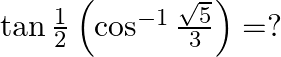
A. 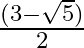
B. 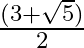
C. 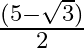
D. 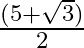
Solution: Option(A) is correct. To Find: The value of $\tan \frac{1}{2}\left(\cos ^{-1} \frac{\sqrt{5}}{3}\right)$ Let, $x=\cos ^{-1} \frac{\sqrt{5}}{3}$ $\Rightarrow \cos x=\frac{\sqrt{5}}{3}$ Now,...
Mark the tick against the correct answer in the following: ![Rendered by QuickLaTeX.com \tan \left[2 \tan ^{-1} \frac{1}{5}-\frac{\pi}{4}\right]=?](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7b682318a7b83adde969470e6e4ef16e_l3.png)
A. 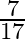
B. 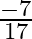
C. 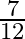
D. 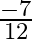
Solution: Option(B) is correct. To Find: The value of $\tan \left(2 \tan ^{-1} \frac{1}{5}-\frac{\pi}{4}\right)$ Consider, $\tan \left(2 \tan ^{-1} \frac{1}{5}-\frac{\pi}{4}\right)=\tan \left(\tan...
Mark the tick against the correct answer in the following: 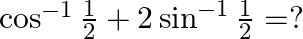
A. 
B. 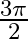
C. 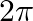
D. none of these
Solution: Option(A) is correct. To Find: The value of $\cos ^{-1} \frac{1}{2}+2 \sin ^{-1} \frac{1}{2}$ Now, let $x=\cos ^{-1} \frac{1}{2}+2 \sin ^{-1} \frac{1}{2}$ $\Rightarrow...
Mark the tick against the correct answer in the following: 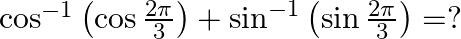
A. 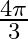
B. 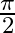
C. 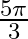
D. 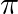
Solution: Option(D) is correct. To Find: The value of $\cos ^{-1}\left(\cos \left(\frac{2 \pi}{3}\right)\right)+\sin ^{-1}\left(\sin \left(\frac{2 \pi}{3}\right)\right)$ Here, consider $\cos...
Mark the tick against the correct answer in the following: If 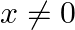 then
then 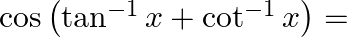 ?
?
A. 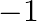
B. 1
C. 0
D. none of these
Solution: Option(C) is correct. Given: $x \neq 0$ To Find: The value of $\cos \left(\tan ^{-1} x+\cot ^{-1} x\right)$ Now, let $x=\cos \left(\tan ^{-1} x+\cot ^{-1} x\right)$ $\begin{array}{l}...
Mark the tick against the correct answer in the following: The value of 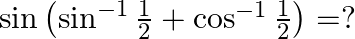
A. 0
B. 1
C. 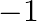
D. none of these
Solution: Option(1) is correct. To Find: The value of $\sin \left(\sin ^{-1} \frac{1}{2}+\cos ^{-1} \frac{1}{2}\right)$ Now, let $x=\sin \left(\sin ^{-1} \frac{1}{2}+\cos ^{-1} \frac{1}{2}\right)$...
Mark the tick against the correct answer in the following: 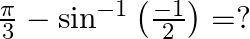
A. 0
B. 
C. 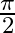
D. 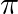
Solution: Option(D) is correct. To Find: The value of $\frac{\pi}{3}-\sin ^{-1}\left(\frac{-1}{2}\right)$ Now, let $x=\frac{\pi}{3}-\sin ^{-1}\left(\frac{-1}{2}\right)$ $\begin{array}{l} \Rightarrow...
Mark the tick against the correct answer in the following: The value of 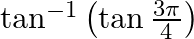 is
is
A. 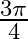
B. 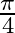
C. 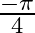
D. none of these
Solution: Option(C) is correct. To Find: The value of $\tan ^{-1}\left(\tan \left(\frac{3 \pi}{4}\right)\right)$ Now, let $x=\tan ^{-1}\left(\tan \left(\frac{3 \pi}{4}\right)\right)$ $\Rightarrow...
Mark the tick against the correct answer in the following: The value of 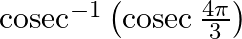 is
is
A. 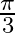
B. 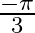
C. 
D. none of these
Solution: Option(B) is correct. To Find: The value of $\operatorname{cosec}^{-1}\left(\operatorname{cosec}\left(\frac{4 \pi}{3}\right)\right)$ Now, let...
Mark the tick against the correct answer in the following: The value of 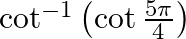 is
is
A. 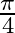
B. 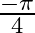
C. 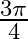
D. none of these
Solution: Option(A) is correct. To Find: The value of $\cot ^{-1}\left(\cot \left(\frac{5 \pi}{4}\right)\right)$ Now, let $x=\cot ^{-1}\left(\cot \left(\frac{5 \pi}{4}\right)\right)$ $\Rightarrow...
Mark the tick against the correct answer in the following: The value of 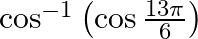 is A.
is A. 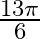 B.
B. 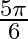 C.
C. 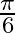 D.
D. 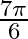
Solution: Option(C) ids correct. To Find: The value of $\cos ^{-1}\left(\cos \left(\frac{13 \pi}{6}\right)\right)$ Now, let $x=\cos ^{-1}\left(\cos \left(\frac{13 \pi}{6}\right)\right)$ $\Rightarrow...
Mark the tick against the correct answer in the following: The principal value of 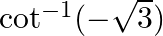 is
is
A. 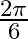
B. 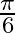
C. 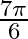
D. 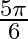
Solution: Option(D) is correct. To Find: The Principle value of $\cot ^{-1}(-\sqrt{3})$ Let the principle value be given by $\mathrm{x}$ Now, let $x=\cot ^{-1}(-\sqrt{3})$ $\begin{array}{l}...
Mark the tick against the correct answer in the following: The principal value of 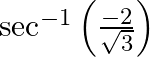 is
is
A. 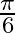
B. 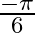
C. 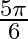
D. 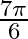
Solution: Option(C) is correct. To Find: The Principle value of $\sec ^{-1}\left(\frac{-2}{\sqrt{3}}\right)$ Let the principle value be given by $x$ Now, let $x=\sec...
Mark the tick against the correct answer in the following: The principal value of 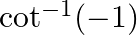 is
is
A. 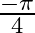
B. 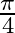
C. 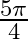
D. 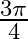
Solution: Option(D) is correct. To Find: The Principle value of $\cot ^{-1}(-1)$ Let the principle value be given by $x$ Now, let $x=\cot ^{-1}(-1)$ $\Rightarrow \cot x=-1$ $\Rightarrow \cot x=-\cot...
Mark the tick against the correct answer in the following: The principal value of 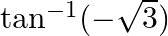 is
is
A. 
B. 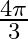
C. 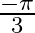
D. none of these
Solution: Option(C) is correct. To Find: The Principle value of $\tan ^{-1}(-\sqrt{3})$ Let the principle value be given by $x$ Now, let $x=\tan ^{-1}(-\sqrt{3})$ $\begin{array}{l} \Rightarrow \tan...
Find the (v) length of the latus rectum of each of the following ellipses. ![Rendered by QuickLaTeX.com \[\mathbf{16}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{16}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c1bda8518d8de0566fb7bb8dae83e7d6_l3.png)
Given: \[\mathbf{16}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{16}\] Divide by \[16\] to both the sides, we get...
Find the (i) lengths of major axes, (ii) coordinates of the vertices ![Rendered by QuickLaTeX.com \[\mathbf{16}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{16}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c1bda8518d8de0566fb7bb8dae83e7d6_l3.png)
Given: \[\mathbf{16}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{16}\] Divide by \[16\] to both the sides, we get...
Find the (iii) coordinates of the foci, (iv) eccentricity ![Rendered by QuickLaTeX.com \[\frac{{{x}^{2}}}{4}+\frac{{{y}^{2}}}{25}=1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2cd71d027e4ee356834184fd92e4f618_l3.png)
![Rendered by QuickLaTeX.com \[\frac{{{x}^{2}}}{4}+\frac{{{y}^{2}}}{25}=1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2cd71d027e4ee356834184fd92e4f618_l3.png)
Given: \[\frac{{{x}^{2}}}{4}+\frac{{{y}^{2}}}{25}=1\]…(i) Since, \[4\text{ }<\text{ }25\] So, above equation is of the form, \[\frac{{{x}^{2}}}{{{b}^{2}}}+\frac{{{y}^{2}}}{{{a}^{2}}}=1\]…(ii)...
Mark the tick against the correct answer in the following: The principal value of 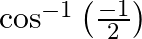 is
is
A. 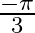
B. 
C. 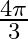
D. 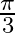
Solution: Option(B) is correct. To Find: The Principle value of $\cos ^{-1}\left(\frac{-1}{2}\right)$ Let the principle value be given by $x$ Now, let $x=\cos ^{-1}\left(\frac{-1}{2}\right)$...
Mark the tick against the correct answer in the following: The principal value of 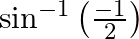 is
is
A. 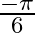
B. 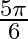
C. 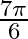
D. none of these
Solution: Option(A) is correct. To Find: The Principle value of $\sin ^{-1}\left(\frac{-1}{2}\right)$ Let the principle value be given by $x$ Now, let $x=\sin ^{-1}\left(\frac{-1}{2}\right)$...
Mark the tick against the correct answer in the following: The principal value of 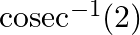 is
is
A. 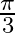
B. 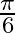
C. 
D. 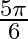
Solution: Option(B) is correct. To Find: The Principle value of $\operatorname{cosec}^{-1}(2)$ Let the principle value be given by $x$ Now, let $x=\operatorname{cosec}^{-1}(2)$ $\begin{array}{l}...
Find the (i) lengths of major axes, (ii) coordinates of the vertices ![Rendered by QuickLaTeX.com \[\mathbf{9}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{16}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{144}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-862342dfce29b8b9c9392c90bd44304d_l3.png)
Given: \[\mathbf{9}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{16}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{144}\] Divide by \[144\] to both the sides, we get...
Mark the tick against the correct answer in the following: The principal value of 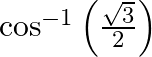 is
is
A. 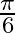
B. 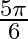
C. 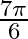
D. none of these
Solution: Option (A) is correct. To Find:The Principle value of $\cos ^{-1}\left(\frac{\sqrt{3}}{2}\right)$ Let the principle value be given by $x$ Now, let $x=\cos...
Write down the interval for the principal-value branch of each of the following functions and draw its graph: 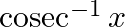
Solution: Principal value branch of $\operatorname{cosec}^{-1} x$ is $\left[-\frac{\pi}{2}, 0\right) \cup\left(0, \frac{\pi}{2}\right]$
Write down the interval for the principal-value branch of each of the following functions and draw its graph: 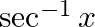
Solution: Principal value branch of $\sec ^{-1} x$ is $\left[0, \frac{\pi}{2}\right) \cup\left(\frac{\pi}{2}, \pi\right]$
Write down the interval for the principal-value branch of each of the following functions and draw its graph: 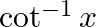
Solution: Principal value branch of $\cot ^{-1} x$ is $(0, \pi)$
Write down the interval for the principal-value branch of each of the following functions and draw its graph: 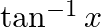
Solution: Principal value branch of $\tan ^{-1} \times$ is $\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$
Write down the interval for the principal-value branch of each of the following functions and draw its graph: 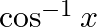
Solution: Principal value branch of $\cos ^{-1} x$ is $[0, \pi]$
Write down the interval for the principal-value branch of each of the following functions and draw its graph: 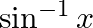
Solution: Principal value branch of $\sin ^{-1} x$ is $\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$
Solve for  :
: 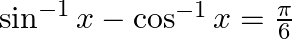
Solution: Given: $\sin ^{-1} x-\cos ^{-1} x=\frac{\pi}{6}$ We know that $\sin ^{-1} \mathrm{x}+\cos ^{-1} \mathrm{x}=\frac{\pi}{2}$ So, $\sin ^{-1} x=\frac{\pi}{2}-\cos ^{-1} x$ Substituting in the...
Solve for  :
: 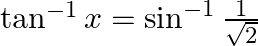
Solution: To find: value of $x$ Given: $\tan ^{-1} \mathrm{x}=\sin ^{-1} \frac{1}{\sqrt{2}}$ We know that $\sin \frac{\pi}{4}=\frac{1}{\sqrt{2}}$ Therefore, $\frac{\pi}{4}=\sin ^{-1}...
Solve for  :
: 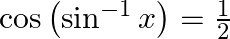
Solution: To find: value of $x$ Given: $\cos \left(\sin ^{-1} \mathrm{x}\right)=\frac{1}{2}$ $\text { LHS }=\cos \left(\sin ^{-1} x\right)$ $\begin{array}{l} =\cos \left(\cos...
Solve for  :
: 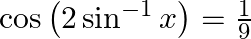
Solution: To find: value of $x$ Formula Used: $2 \sin ^{-1} x=\sin ^{-1}\left(2 x \sqrt{1-x^{2}}\right)$. Given: $\cos \left(2 \sin ^{-1} x\right)=\frac{1}{9}$ $\text { LHS }=\cos \left(2 \sin ^{-1}...
Solve for 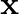 :
: 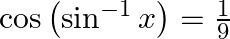
Solution: To find: value of $x$ Given: $\cos \left(\sin ^{-1} x\right)=\frac{1}{9}$ $\mathrm{LHS}=\cos \left(\sin ^{-1} \mathrm{x}\right) \ldots(1)$ Let $\sin \theta=x$ Therefore $\theta=\sin ^{-1}...
Solve for x: 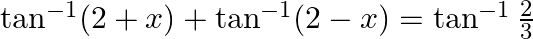
Solution: To find: value of $x$ Formula Used: $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$ where xy $<1$ Given: $\tan ^{-1}(2+x)+\tan ^{-1}(2-x)=\tan ^{-1} \frac{2}{3}$...
Solve for  :
: 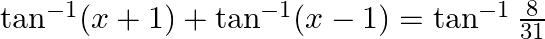
Solution: To find: value of $x$ Formula Used: $\tan ^{-1} \mathrm{x}+\tan ^{-1} \mathrm{y}=\tan ^{-1}\left(\frac{\mathrm{x}+y}{1-\mathrm{xy}}\right)$ where $\mathrm{xy}<1$ Given: $\tan...
Prove that: 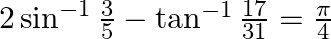
Solution: To Prove: $2 \sin ^{-1} \frac{3}{5}-\tan ^{-1} \frac{17}{31}=\frac{\pi}{4}$ Formula Used: 1) $2 \sin ^{-1} x=\sin ^{-1}\left(2 x \times \sqrt{1-x^{2}}\right)$ 2) $\tan ^{-1}...
Prove that: 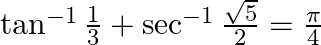
Solution: To Prove: $\tan ^{-1} \frac{1}{3}+\sec ^{-1} \frac{\sqrt{5}}{2}=\frac{\pi}{4}$ Formula Used: $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$ where $x y<1$ Proof:...
Prove that: 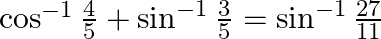
Solution: To Prove: $\cos ^{-1} \frac{4}{5}+\sin ^{-1} \frac{3}{5}=\sin ^{-1} \frac{27}{11}$ Formula Used: $\sin ^{-1} x+\sin ^{-1} y=\sin ^{-1}\left(x \times \sqrt{1-y^{2}}+y \times...
Prove that: 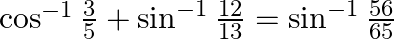
Solution: To Prove: $\cos ^{-1} \frac{3}{5}+\sin ^{-1} \frac{12}{13}=\sin ^{-1} \frac{56}{65}$ Formula Used: $\sin ^{-1} \mathrm{x}+\sin ^{-1} \mathrm{y}=\sin ^{-1}\left(\mathrm{x} \times...
Prove that: 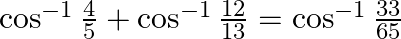
Solution: To Prove: $\cos ^{-1} \frac{4}{5}+\cos ^{-1} \frac{12}{13}=\cos ^{-1} \frac{33}{65}$ Formula Used: $\cos ^{-1} x+\cos ^{-1} y=\cos ^{-1}\left(x y-\sqrt{1-x^{2}} \times...
Prove that: 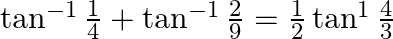
Solution: To Prove: $\tan ^{-1} \frac{1}{4}+\tan ^{-1} \frac{2}{9}=\frac{1}{2} \tan ^{-1} \frac{4}{3} \Rightarrow 2\left(\tan ^{-1} \frac{1}{4}+\tan ^{-1} \frac{2}{9}\right)=\tan ^{-1} \frac{4}{3}$...
Prove that: 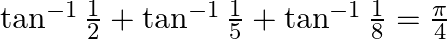
Solution: To Prove: $\tan ^{-1} \frac{1}{2}+\tan ^{-1} \frac{1}{5}+\tan ^{-1} \frac{1}{8}=\frac{\pi}{4}$ Formula Used: $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$ where $x...
Prove that: 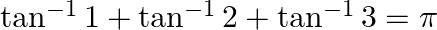
Solution: To Prove: $\tan ^{-1} 1+\tan ^{-1} 2+\tan ^{-1} 3=\pi$ Formula Used: $\tan ^{-1} \mathrm{x}+\tan ^{-1} \mathrm{y}=\pi+\tan ^{-1}\left(\frac{\mathrm{x}+\mathrm{y}}{1-\mathrm{xy}}\right)$...
Prove that: 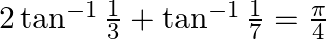
Solution: To Prove: $2 \tan ^{-1} \frac{1}{3}+\tan ^{-1} \frac{1}{7}=\frac{\pi}{4}$ Formula Used: $\tan ^{-1} \mathrm{x}+\tan ^{-1} \mathrm{y}=\tan...
Prove that: 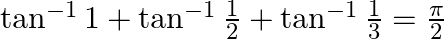
Solution: To Prove: $\tan ^{-1} 1+\tan ^{-1} \frac{1}{2}+\tan ^{-1} \frac{1}{3}=\frac{\pi}{2}$ Formula Used: $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$ Proof:...
Prove that: 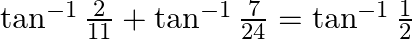
Solution: To Prove: $\tan ^{-1} \frac{2}{11}+\tan ^{-1} \frac{7}{24}=\tan ^{-1} \frac{1}{2}$ Formula Used: $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$ Proof:...
Prove that: 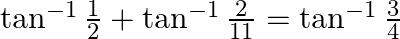
Solution: To Prove: $\tan ^{-1} \frac{1}{2}+\tan ^{-1} \frac{2}{11}=\tan ^{-1} \frac{3}{4}$ Formula Used: $\tan ^{-1} \mathrm{x}+\tan ^{-1} \mathrm{y}=\tan...
Prove that: 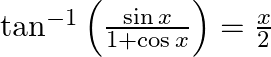
Solution: To Prove: $\tan ^{-1}\left(\frac{\sin x}{1+\cos x}\right)=\frac{x}{2}$ Formula Used: 1) $\sin A=2 \times \sin \frac{A}{2} \times \cos \frac{A}{2}$ 2) $1+\cos A=2 \cos ^{2} \frac{A}{2}$...
Prove that: 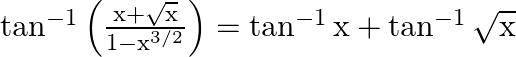
Solution: We know that, $\tan ^{-1}\left(\frac{A+B}{1-A B}\right)=\tan ^{-1} A+\tan ^{-1} B$ Now, taking $A=x$ and $B=\sqrt{x}$ We get, $\tan ^{-1} x+\tan ^{-1} \sqrt{x}=\tan...
Prove that: 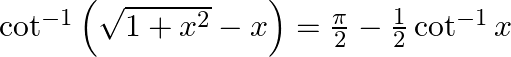
Solution: To Prove: $\cot ^{-1}\left(\sqrt{1+x^{2}}-x\right)=\frac{\pi}{2}-\frac{1}{2} \cot ^{-1} x$ Formula Used: 1) $\tan \left(\frac{\pi}{4}+A\right)=\frac{1+\tan A}{1-\tan A}$ 2)...
Prove that: 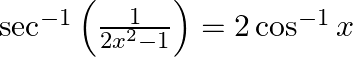
Solution: To Prove: $\sec ^{-1}\left(\frac{1}{2 x^{2}-1}\right)=2 \cos ^{-1} x$ Formula Used: 1) $\cos 2 A=2 \cos ^{2} A-1$ 2) $\cos ^{-1} A=\sec ^{-1}\left(\frac{1}{A}\right)$ Proof:...
Prove that: 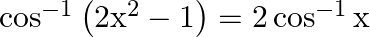
Solution: To Prove: $\cos ^{-1}\left(2 x^{2}-1\right)=2 \cos ^{-1} x$ Formula Used: $\cos 2 A=2 \cos ^{2} A-1$ Proof: $\text { LHS }=\cos ^{-1}\left(2 x^{2}-1\right) \ldots(1)$ Let $x=\cos A \ldots$...
Prove that: 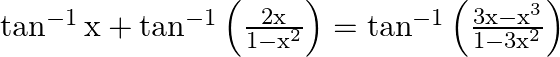
Solution: To Prove: $\tan ^{-1} x+\tan ^{-1}\left(\frac{2 x}{1-x^{2}}\right)=\tan ^{-1}\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right)$ Formula Used: $\tan ^{-1} x+\tan ^{-1} y=\tan...
Prove that: 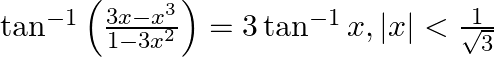
Solution: To Prove: $\tan ^{-1}\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right)=3 \tan ^{-1} x$ Formula Used: $\tan 3 A=\frac{3 \tan A-\tan ^{3} A}{1-3 \tan ^{2} A}$ Proof: $\text { LHS }=\tan...
Prove that: 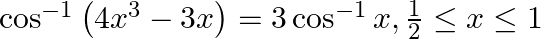
Solution: To Prove: $\cos ^{-1}\left(4 x^{3}-3 x\right)=3 \cos ^{-1} x$ Formula Used: $\cos 3 A=4 \cos ^{3} A-3 \cos A$ Proof: $\text { LHS }=\cos ^{-1}\left(4 x^{3}-3 x\right) \ldots(1)$ Let...
Prove that: 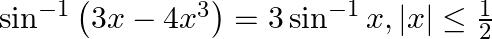
Solution: To Prove: $\sin ^{-1}\left(3 x-4 x^{3}\right)=3 \sin ^{-1} x$ Formula Used: $\sin 3 \mathrm{~A}=3 \sin \mathrm{A}-4 \sin ^{3} \mathrm{~A}$ Proof: $\operatorname{LHS}=\sin ^{-1}\left(3 x-4...
Prove that: 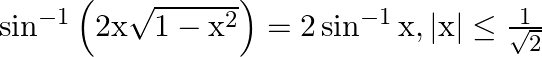
Solution: To Prove: $\sin ^{-1}\left(2 x \sqrt{1-x^{2}}\right)=2 \sin ^{-1} x$ Formula Used: $\sin 2 A=2 \times \sin A \times \cos A$ Proof: $\text { LHS }=\sin ^{-1}\left(2 x \sqrt{1-x^{2}}\right)...
Prove that: 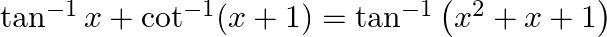
Solution: To Prove: $\tan ^{-1} x+\cot ^{-1}(x+1)=\tan ^{-1}\left(x^{2}+x+1\right)$ Formula Used: 1) $\cot ^{-1} \mathrm{x}=\tan ^{-1} \frac{1}{\mathrm{x}}$ 2) $\tan ^{-1} \mathrm{x}+\tan ^{-1}...
Find the principal value of each of the following: 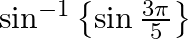
Solution: $\begin{array}{l} \sin ^{-1}\left\{\sin \left(\frac{3 \pi}{5}\right)\right\} \\ =\sin ^{-1}\left\{\sin \left(\pi-\frac{2 \pi}{5}\right)\right\} \end{array}$ [Formula: $\sin (\pi-x)=\sin...
Find the principal value of each of the following : 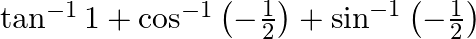
Solution: [Formula: $\cos ^{-1}(-x)=\pi-\cos (x)$ and $\left.\sin ^{-1}(-x)=-\sin (x)\right]$ $\tan ^{-1} 1+\left(\pi-\cos ^{-1}\left(\frac{1}{2}\right)\right)+\left(-\sin...
Find the principal value of each of the following : 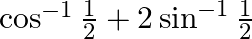
Solution: Putting the values of the inverse trigonometric terms $\begin{array}{l} \frac{\pi}{3}+2 \times \frac{\pi}{6} \\ =\frac{\pi}{3}+\frac{\pi}{3} \\ =\frac{2 \pi}{3} \end{array}$
Find the principal value of each of the following : 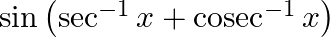
Solution: $\sin \left(\sec ^{-1} x+\operatorname{cosec}^{-1} x\right)=\sin \left(\frac{\pi}{2}\right)$ [Formula: $\left.\sec ^{-1} x+\operatorname{cosec}^{-1} x=\frac{\pi}{2}\right]$ Putting the...
Find the principal value of each of the following : 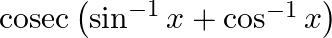
Solution: $\operatorname{cosec}\left(\sin ^{-1} x+\cos ^{-1} x\right)=\operatorname{cosec} \frac{\pi}{2}\left[\right.$ Formula: $\left.\sin ^{-1} x+\cos ^{-1} x=\frac{\pi}{2}\right]$ Putting the...
Find the principal value of each of the following: 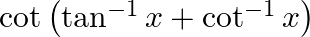
Solution: $\cot \left(\tan ^{-1} x+\cot ^{-1} x\right)=\cot \left(\frac{\pi}{2}\right)$ [Formula: $\left.\tan ^{-1} x+\cot ^{-1} x=\frac{\pi}{2}\right]$ Putting value of $\cot...
Find the principal value of each of the following : 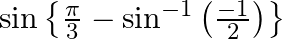
Solution: $\begin{array}{l} \sin \left\{\frac{\pi}{3}-\sin ^{-1}\left(\frac{-1}{2}\right)\right\}\left[\text { Formula: } \sin ^{-1}(-\mathrm{x})=-\sin ^{-1} \mathrm{x}\right] \\ =\sin...
Find the principal value of each of the following : 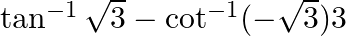
Solution: $\tan ^{-1} \sqrt{3}-\cot ^{-1}(-\sqrt{3})$ Putting the value of $\tan ^{-1} \sqrt{3}$ and using the formula $\begin{array}{l} \cot ^{-1}(-x)=\pi-\cot ^{-1} x \\...
Find the principal value of each of the following : 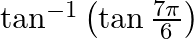
Solution: $\tan ^{-1}\left(\tan \frac{7 \pi}{6}\right)=\tan ^{-1}\left(\tan \left(\pi+\frac{\pi}{6}\right)\right)$ [ Formula: $\tan (\pi+x)=\tan x$, as tan is positive in the third quadrant.] $=\tan...
Find the principal value of each of the following : 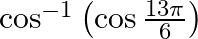
Solution: $\cos ^{-1}\left(\cos \frac{13 \pi}{6}\right)=\cos ^{-1}\left(\cos \left(2 \pi+\frac{\pi}{6}\right)\right)$ [ Formula: $\cos (2 \pi+x)=\cos x, \cos$ is positive in the first quadrant. ]...
Find the principal value of each of the following : 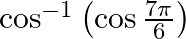
Solution: $\cos ^{-1}\left(\cos \frac{7 \pi}{6}\right)=\cos ^{-1}\left(\cos \left(2 \pi-\frac{5 \pi}{6}\right)\right)$ [Formula: $\cos (2 \pi-x)=\cos (x)$, as cos has a positive vaule in the fourth...
Find the principal value of each of the following : 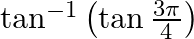
Solution: $\tan ^{-1}\left(\tan \frac{3 \pi}{4}\right)=\tan ^{-1}\left(\tan \left(\pi-\frac{\pi}{4}\right)\right)$ [Formula: $\tan (\pi-x)=-\tan (x)$, as tan is negative in the second quadrant. ]...
Find the principal value of each of the following : 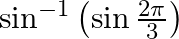
Solution: $\sin ^{-1}\left(\sin \frac{2 \pi}{3}\right)=\sin ^{-1}\left(\sin \left(\pi-\frac{\pi}{3}\right)\right)$ [ Formula: $\sin (\pi-x)=\sin x)$ $=\sin ^{-1}\left(\sin \frac{\pi}{3}\right)$ [...
Find the principal value of each of the following : 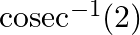
Solution: $\operatorname{cosec}^{-1}(2)$ Putting the value directly $=\frac{\pi}{6}$
Find the principal value of each of the following : 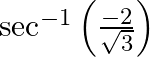
Solution: $\sec ^{-1}\left(\frac{-2}{\sqrt{3}}\right)=\pi-\sec ^{-1}\left(\frac{2}{\sqrt{3}}\right)\left[\right.$ Formula: $\left.\sec ^{-1}(-x)=\pi-\sec ^{-1}(x)\right]$ $\begin{array}{l}...
Find the principal value of each of the following : 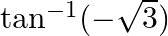
Solution: $\tan ^{-1}(-\sqrt{3})=-\tan ^{-1}(\sqrt{3})$ [Formula: $\left.\tan ^{-1}(-x)=-\tan ^{-1}(x)\right]$ $=-\frac{\pi}{3}$
Find the principal value of each of the following : 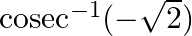
Solution: $\operatorname{cosec}^{-1}(-\sqrt{2})=-\operatorname{cosec}^{-1}(\sqrt{2})$ [Formula: $\left.\operatorname{cosec}^{-1}(-x)=-\operatorname{cosec}^{-1}(x)\right]$ $=-\frac{\pi}{4}$ This can...
Find the principal value of each of the following : 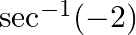
Solution: $\sec ^{-1}(-2)=\pi-\sec ^{-1}(2)\left[\right.$ Formula: $\left.\sec ^{-1}(-x)=\pi-\sec ^{-1}(x)\right]$ $\begin{array}{l} =\pi-\frac{\pi}{3} \\ =\frac{2 \pi}{3} \end{array}$
Find the principal value of each of the following : 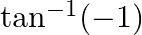
Solution: $\tan (-1)=-\tan (1)\left[\right.$ Formula: $\left.\tan ^{-1}(-x)=-\tan ^{-1}(x)\right]$ [ We know that $\tan \frac{\pi}{4}=1$, thus $\left.\tan ^{-1} \frac{\pi}{4}=1\right]$...
Find the principal value of each of the following : 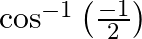
Solution: $\cos ^{-1}\left(\frac{-1}{2}\right)=\pi-\cos ^{-1}\left(\frac{1}{2}\right)$ [ Formula: $\left.\cos ^{-1}(-x)=-\cos ^{-1}(x)\right]$ $=\pi-\frac{\pi}{3}$ $=\frac{2 \pi}{3}$
Find the principal value of each of the following : 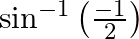
Solution: $\sin ^{-1}\left(\frac{-1}{2}\right)=-\sin ^{-1}\left(\frac{1}{2}\right)\left[\right.$ Formula: $\left.\sin ^{-1}(-x)=\sin ^{-1}(x)\right]$ $=-\frac{\pi}{6}$
If 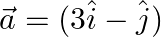 and
and 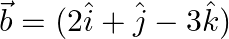 then express
then express 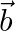 in the form
in the form  , where
, where 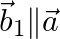 and
and  .
.
Solution: $\begin{array}{l} \vec{a}=3 \hat{\imath}-\hat{\jmath} \end{array}$ $\begin{array}{l} \mathrm{I} \vec{a} \mathrm{I}=\sqrt{3^{2}+1^{2}}=\sqrt{9+1}=\sqrt{10} \\ \hat{a}=\frac{3}{\sqrt{10}}...
If 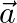 and
and 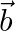 are two vectors such that
are two vectors such that 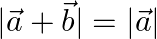 then prove that vector
then prove that vector 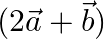 is perpendicular to the vector
is perpendicular to the vector 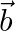 .
.
Solution: $\begin{array}{l} \mathrm{I} \vec{a}+\vec{b} \mathrm{I}=\vec{a} \\ (\vec{a}+\vec{b}) \cdot(\vec{a}+\vec{b})=\vec{a} \cdot \vec{a} \\ \mathrm{I} \vec{a} \mathrm{I}_{2}+\vec{a} \cdot...
If 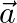 and
and 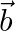 are two unit vectors such that
are two unit vectors such that 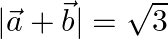 , find
, find 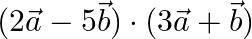 .
.
Solution: $\vec{a}$ and $\vec{b}$ are unit vectors $\begin{array}{l} (\vec{a}+\vec{b}) \cdot(\vec{a}+\vec{b})=\mathrm{I}(\vec{a}+\vec{b}) \mathrm{I}_{2} \\ \mathrm{I} \vec{a}...
Three vertices of a triangle are 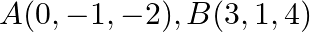 and
and 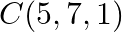 . Show that it is a right – angled triangle. Also, find its other two angles.
. Show that it is a right – angled triangle. Also, find its other two angles.
Solution: $\overrightarrow{O A}=-\hat{\jmath}-2 \hat{k}$ $\overrightarrow{O B}=3 \hat{\imath}+\hat{\jmath}+4 \hat{k}$ $\overrightarrow{O C}=5 \hat{\imath}+7 \hat{\jmath}+\hat{k}$ $\overrightarrow{O...
Find the value of 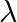 for which the vectors
for which the vectors 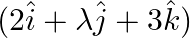 and
and 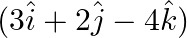 are perpendicular to each other.
are perpendicular to each other.
Solution: $\begin{array}{l} \vec{a}=2 \hat{\imath}+\lambda \hat{\jmath}+3 \hat{k} \\ \vec{b}=3 \hat{\imath}+2 \hat{\jmath}-4 \hat{k} \end{array}$ Given $\vec{a} \perp \vec{b}$ $\begin{array}{l}...
If 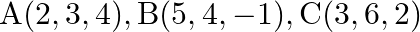 and
and 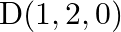 be four points, show that
be four points, show that 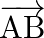 is perpendicular to
is perpendicular to  .
.
Solution: $\begin{array}{l} \overrightarrow{O A}=2 \hat{\imath}+3 \hat{\jmath}+4 \hat{k} \\ \overrightarrow{O B}=5 \hat{\imath}+4 \hat{\jmath}-\hat{k} \\ \overrightarrow{O C}=3 \hat{\imath}+6...
If 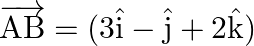 and the coordinates of
and the coordinates of 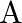 are
are 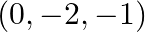 , find the coordinates of
, find the coordinates of 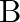 .
.
Solution: $\begin{array}{l} \overrightarrow{A B}=3 \hat{\imath}-\hat{\jmath}+2 \hat{k} \\ \overrightarrow{O A}=-2 \hat{\jmath}-\hat{k} \\ \overrightarrow{A B}=\overrightarrow{O B}-\overrightarrow{O...
The dot products of a vector with the vector 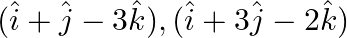 and
and 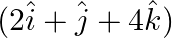 are 0,5 and 8 respectively. Find the vector.
are 0,5 and 8 respectively. Find the vector.
Solution: $\begin{array}{l} \vec{v}=\mathrm{v} 1 \hat{\imath}+\mathrm{v} 2 \hat{\jmath}+\mathrm{v}_{3} \hat{k} \\ \vec{a}=\hat{\imath}+3 \hat{\jmath}-2 \hat{k} \\...
If 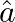 and
and 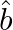 are unit vectors inclined at an angle
are unit vectors inclined at an angle 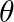 then prove that:
then prove that:
i. 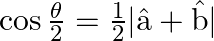
ii. 
Solution: $\hat{a}$ and $\hat{b}$ are unit vectors inclined at an angle $\theta$ i) $\begin{aligned} &(\hat{a}+\hat{b})(\hat{a}+\hat{b})=\mathrm{I} \hat{\mathrm{a}} \mathrm{I}_{2}+\mathrm{I}...
If 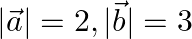 and
and 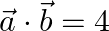 , find
, find 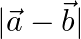 .
.
Solution: $\mathrm{I} \overrightarrow{\mathrm{a}} \mathrm{I}=2$ $\mathrm{I} \vec{b} \mathrm{I}=3$ $\vec{a} \cdot \vec{b}=4$ $(\vec{a}-\vec{b}) \cdot(\vec{a}-\vec{b})=\mathrm{I} \vec{a}...
Find the angle between 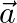 and
and 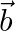 , when
, when
i.  and
and 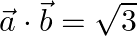
ii. 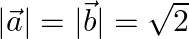 and
and 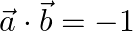
Solution: i) $\mathrm{I} \vec{a} \mathrm{I}=2$ $\mid \vec{b} \mathrm{I}=1$ $\vec{a} \cdot \vec{b}=\sqrt{3}$ $\mathrm{I} \vec{a} \mathrm{I} . \mid \vec{b} \mathrm{I} \cos \theta=\sqrt{3}$ $2 \cos...
Prove that 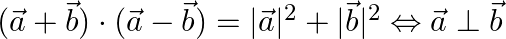 , where
, where 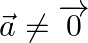 and
and 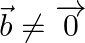 .
.
Solution: $\begin{array}{l} (\vec{a}+\vec{b}) \cdot(\vec{a}-\vec{b})=\mathrm{I} \vec{a} \mathrm{I}_{2}+\mathrm{I} \vec{b} \mathrm{I}_{2} \\ \mathrm{I} \vec{a} \mathrm{I}_{2}-\mathrm{I} \vec{b}...
