Solution: Option(C) is correct. To Find: The Domain of $\sec ^{-1}(x)$ Here,the inverse function is given by $y=f^{-1}(x)$ The graph of the function $y=\sec ^{-1}(x)$ can be obtained from the graph...
Mark the tick against the correct answer in the following: Domain of
Mark the tick against the correct answer in the following: Domain of 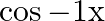 is
is
A. ![Rendered by QuickLaTeX.com [0,1]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a172ffb7f81d132bb8f882837e234a51_l3.png)
B. ![Rendered by QuickLaTeX.com [-1,1]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-bd9ec9b7fdf72f6f954becf26cf7129a_l3.png)
C. ![Rendered by QuickLaTeX.com [-1,0]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-8752afe84dfa40e1f5916867a3991fed_l3.png)
D. None of these
Solution: Option(B) is correct. To Find: The Domain of $\cos ^{-1}(x)$ Here,the inverse function of $\cos$ is given by $y=f^{-1}(x)$ The graph of the function $y=\cos ^{-1}(x)$ can be obtained from...
Mark the tick against the correct answer in the following: Range of 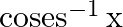 is
is
A. 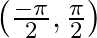
B. ![Rendered by QuickLaTeX.com \left[\frac{-\pi}{2}, \frac{\pi}{2}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d03f7933dddf8dbceee8c92c85707a25_l3.png)
C. ![Rendered by QuickLaTeX.com \left[\frac{-\pi}{2}, \frac{\pi}{2}\right]-\{0\}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c1b4b19d92f0ad0d4cedf9d79013a65d_l3.png)
D. None of these
Solution: Option(C) is correct. To Find: The range of $\operatorname{cosec}^{-1}(x)$ Here,the inverse function is given by $\mathrm{y}=\mathrm{f}^{-1}(x)$ The graph of the function...
Mark the tick against the correct answer in the following: Range of 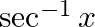 is
is
A. ![Rendered by QuickLaTeX.com \left[0, \frac{\pi}{2}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-cdf7f72b896a3c8ef3745557ca17a3c9_l3.png)
B. ![Rendered by QuickLaTeX.com [0, \pi]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3ee8a7f2b7324e2152a4807a1b912cfc_l3.png)
C. ![Rendered by QuickLaTeX.com [0, \pi]-\left\{\frac{\pi}{2}\right\}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c7ddbce50a6e98fb8f2a1854735e3fac_l3.png)
D. None of these
Solution: Option(C) is correct. To Find:The range of $\sec ^{-1}(x)$ Here,the inverse function is given by $y=f^{-1}(x)$ The graph of the function $y=\sec ^{-1}(x)$ can be obtained from the graph of...
Mark the tick against the correct answer in the following: Range of 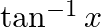 is
is
A. 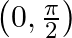
B. 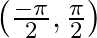
C. ![Rendered by QuickLaTeX.com \left[\frac{\pi}{2}, \frac{\pi}{2}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-ed1b0c0afbc8394951aac5d699c6de92_l3.png)
D. None of these
Solution: Option(B) is correct. To Find: The range of $\tan ^{-1} x$ Here, the inverse function is given by $y=f^{-1}(x)$ The graph of the function $y=\tan ^{-1}(x)$ can be obtained from the graph...
Mark the tick against the correct answer in the following: Range of 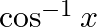 is
is
A. ![Rendered by QuickLaTeX.com [0, \pi]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3ee8a7f2b7324e2152a4807a1b912cfc_l3.png)
B. ![Rendered by QuickLaTeX.com \left[0, \frac{\pi}{2}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-cdf7f72b896a3c8ef3745557ca17a3c9_l3.png)
C. ![Rendered by QuickLaTeX.com \left[\frac{-\pi}{2}, \frac{\pi}{2}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d03f7933dddf8dbceee8c92c85707a25_l3.png)
D. None of these
Solution: Option(A) is correct. To Find: The range of $\cos ^{-1} x$ Here, the inverse function is given by $\mathrm{y}=\mathrm{f}^{-1}(x)$ The graph of the function $y=\cos ^{-1}(x)$ can be...
Mark the tick against the correct answer in the following: Range of 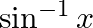 is
is
A. ![Rendered by QuickLaTeX.com \left[0, \frac{\pi}{2}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-cdf7f72b896a3c8ef3745557ca17a3c9_l3.png)
B. ![Rendered by QuickLaTeX.com [0, \pi]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3ee8a7f2b7324e2152a4807a1b912cfc_l3.png)
C. ![Rendered by QuickLaTeX.com \left[\frac{-\pi}{2}, \frac{\pi}{2}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d03f7933dddf8dbceee8c92c85707a25_l3.png)
D. None of these
Solution: Option() is correct. To Find: The range of $\sin ^{-1} x$ Here,the inverse function is given by $\mathrm{y}=\mathrm{f}^{-1}(x)$ The graph of the function $y=\sin ^{-1}(x)$ can be obtained...
Mark the tick against the correct answer in the following: 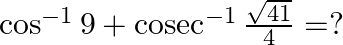
A. 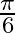
B. 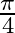
C. 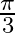
D. 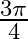
Solution: Option(B) is correct. To Find: The value of $\cot ^{-1} 9+\operatorname{cosec}^{-1} \frac{\sqrt{41}}{4}$ Now $\cot ^{-1} 9+\operatorname{cosec}^{-1} \frac{\sqrt{41}}{4}$ can be written in...
Mark the tick against the correct answer in the following: 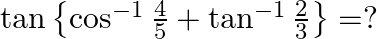
A. 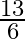
B. 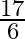
C. 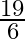
D. 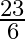
Solution: Option(B) is correct. To Find: The value of $\tan \left\{\cos ^{-1} \frac{4}{5}+\tan ^{-1} \frac{2}{3}\right\}$ Let $x=\cos ^{-1} \frac{4}{5}$ $\Rightarrow \cos x=\frac{4}{5}=\frac{\text {...
Mark the tick against the correct answer in the following: If 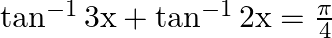 then
then 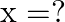
A. 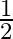 or
or 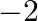
B. 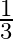 or
or 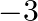
C. 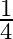 or
or 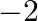
D. 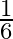 or
or 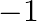
Solution: Option(D) is correct. Given: $\tan ^{-1} 3 x+\tan ^{-1} 2 x=\frac{\pi}{4}$ To Find: The value of $x$ Since we know that $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$...
Mark the tick against the correct answer in the following: If 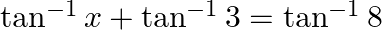 then
then 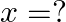
A. 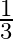
B. 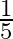
C. 3
D. 5
Solution: Option(B) is correct. Given: $\tan ^{-1} x+\tan ^{-1} 3=\tan ^{-1} 8$ To Find: The value of $x$ Here $\tan ^{-1} x+\tan ^{-1} 3=\tan ^{-1} 8$ can be written as $\tan ^{-1} x=\tan ^{-1}...
Mark the tick against the correct answer in the following: 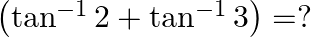
A. 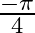
B. 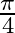
C. 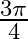
D. 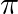
Solution: Option(C) is correct. To Find: The value of $\tan ^{-1} 2+\tan ^{-1} 3$ Since we know that $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$ $\begin{array}{l}...
If 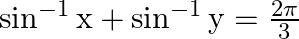 then
then 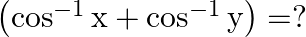
A. 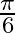
B. 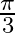
C. 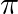
D. 
Solution: Option(B) is correct. Given: $\sin ^{-1} x+\sin ^{-1} y=\frac{2 \pi}{3}$ To Find: The value of $\cos ^{-1} x+\cos ^{-1} y$ Since we know that $\sin ^{-1} x+\cos ^{-1} x=\frac{\pi}{2}$...
Mark the tick against the correct answer in the following: If 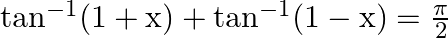 then
then 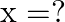
A. 1
B. 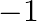
C. 0
D. 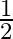
Solution: Option(C) is correct. To Find: The value of $\tan ^{-1}(1+x)+\tan ^{-1}(1-x)=\frac{\pi}{2}$ Since we know that $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$...
Mark the tick against the correct answer in the following: If 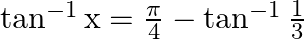 then
then 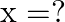
A. 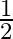
B. 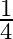
C. 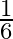
D. None of these
Solution: Option(A) is correct. To Find: The value of $\tan ^{-1} x=\frac{\pi}{4}-\tan ^{-1} \frac{1}{3}$ Now, $\tan ^{-1} x=\tan ^{-1} 1-\tan ^{-1} \frac{1}{3}\left(\because \tan...
Mark the tick against the correct answer in the following: ![Rendered by QuickLaTeX.com \sin \left[2 \sin ^{-1} \frac{4}{5}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-0ba2302a863f7b2f0171a3e761c4be13_l3.png)
A. 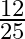
B. 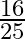
C. 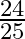
D. None of these
Solution: Option(C) is correct. To Find: The value of $\sin \left(2 \sin ^{-1} \frac{4}{5}\right)$ Let, $x=\sin ^{-1} \frac{4}{5}$ $\Rightarrow \sin x=\frac{4}{5}$ We know that , $\cos...
Mark the tick against the correct answer in the following: ![Rendered by QuickLaTeX.com \sin \left[2 \tan ^{-1} \frac{5}{8}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-111a4736820b38750893122ca95b27ed_l3.png)
A. 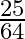
B. 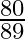
C. 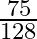
D. none of these
Solution: Option(B) is correct. To Find: The value of $\sin \left(2 \tan ^{-1} \frac{5}{8}\right)$ Let, $x=\sin \left(2 \tan ^{-1} \frac{5}{8}\right)$ We know that $2 \tan ^{-1} x=\sin...
Mark the tick against the correct answer in the following: 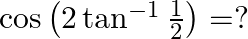
A. 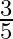
B. 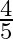
C. 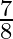
D. none of these
Solution: Option(A) is correct. To Find: The value of $\cos \left(2 \tan ^{-1} \frac{1}{2}\right)$ Let, $x=\cos \left(2 \tan ^{-1} \frac{1}{2}\right)$ $\Rightarrow \mathrm{x}=\cos \left(\tan ^{-1}...
Mark the tick against the correct answer in the following: 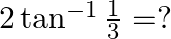
A. 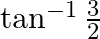
B. 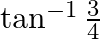
C. 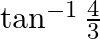
D. none of these
Solution: Option(B) is correct. To Find: The value of $2 \tan ^{-1} \frac{1}{3}$ i.e, $\tan ^{-1} \frac{1}{3}+\tan ^{-1} \frac{1}{3}$ Let, $x=\tan ^{-1} \frac{1}{3}+\tan ^{-1} \frac{1}{3}$ Since we...
Mark the tick against the correct answer in the following: 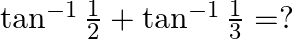
A. 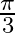
B. 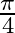
C. 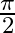
D. 
Solution: Option(B) is correct. To Find: The value of $\tan ^{-1} \frac{1}{2}+\tan ^{-1} \frac{1}{3}$ Let, $x=\tan ^{-1} \frac{1}{2}+\tan ^{-1} \frac{1}{3}$ Since we know that $\tan ^{-1} x+\tan...
Mark the tick against the correct answer in the following: 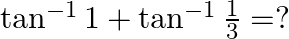
A. 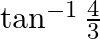
B. 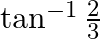
C. 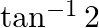
D. 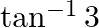
Solution: Option(C) is correct. To Find: The value of $\tan ^{-1} 1+\tan ^{-1} \frac{1}{3}$ Let, $x=\tan ^{-1} 1+\tan ^{-1} \frac{1}{3}$ Since we know that $\tan ^{-1} x+\tan ^{-1} y=\tan...
Mark the tick against the correct answer in the following: 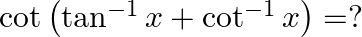
A. 1
B. 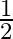
C. 0
D. none of these
Solution: Option(C) is correct. To Find: The value of $\cot \left(\tan ^{-1} x+\cot ^{-1} x\right)$ Let, $x=\cot \left(\tan ^{-1} x+\cot ^{-1} x\right)$ $\begin{array}{l} \Rightarrow \mathrm{x}=\cot...
Mark the tick against the correct answer in the following: 
A. 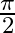
B. 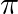
C. 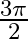
D. 
Solution: Option(A) is correct. To Find: The value of $\tan ^{-1}(-1)+\cos ^{-1}\left(\frac{-1}{\sqrt{2}}\right)$ Let, $x=\tan ^{-1}(-1)+\cos ^{-1}\left(\frac{-1}{\sqrt{2}}\right)$ $\Rightarrow...
Mark the tick against the correct answer in the following: 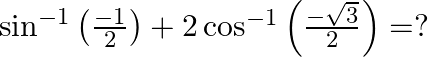
A. 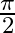
B. 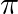
C. 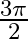
D. none of these
Solution: Option(C) is correct. To Find: The value of $\sin ^{-1}\left(\frac{-1}{2}\right)+2 \cos ^{-1}\left(\frac{-\sqrt{3}}{2}\right)$ Let, $x=\sin ^{-1}\left(\frac{-1}{2}\right)+2 \cos...
Mark the tick against the correct answer in the following: If 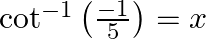 then
then 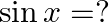
A. 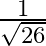
B. 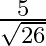
C. 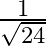
D. none of these
Solution: Option(B) is correct. Given: $\cot ^{-1} \frac{-1}{5}=x$ To Find: The value of $\sin \mathrm{x}$ Since, $x=\cot ^{-1} \frac{-1}{5}$ $\Rightarrow \cot \mathrm{x}=\frac{-1}{5}=\frac{\text {...
Mark the tick against the correct answer in the following: 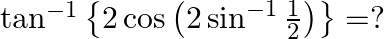
A. 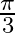
B. 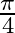
C. 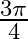
D. 
Solution: Option(B) is correct. To Find: The value of $\tan ^{-1}\left\{2 \cos \left(2 \sin ^{-1} \frac{1}{2}\right)\right\}$ Let, $x=\tan ^{-1}\left\{2 \cos \left(2 \sin ^{-1}...
Mark the tick against the correct answer in the following: 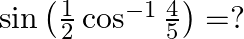
A. 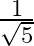
B. 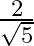
C. 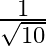
D. 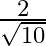
Solution: Option(C) is correct. To Find: The value of $\sin \left(\frac{1}{2} \cos ^{-1} \frac{4}{5}\right)$ Let $x=\cos ^{-1} \frac{4}{5}$ $\Rightarrow \cos x=\frac{4}{5}$ Therefore $\sin...
Mark the tick against the correct answer in the following: 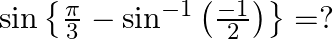
A. 1
B. 0
C. 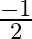
D. none of these
Solution: Option(A) is correct. To Find: The value of of $\sin \left\{\frac{\pi}{3}-\sin ^{-1}\left(\frac{-1}{2}\right)\right\}$ Let, $x=\sin \left\{\frac{\pi}{3}-\sin...
Mark the tick against the correct answer in the following: 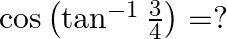
A. 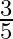
B. 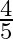
C. 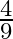
D. none of these
Solution: Option(B) is correct. To Find: The value of $\cos \left(\tan ^{-1} \frac{3}{4}\right)$ Let $x=\tan ^{-1} \frac{3}{4}$ $\begin{array}{l} \Rightarrow \tan x=\frac{3}{4} \\ \Rightarrow \tan...
Mark the tick against the correct answer in the following: 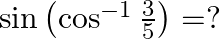
A. 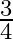
B. 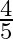
C. 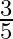
D. none of these
Solution: Option(B) is correct. To Find: The value of $\sin \left(\cos ^{-1} \frac{3}{5}\right)$ Let, $x=\cos ^{-1} \frac{3}{5}$ $\Rightarrow \cos x=\frac{3}{5}$ Now, $\sin \left(\cos ^{-1}...
Mark the tick against the correct answer in the following: 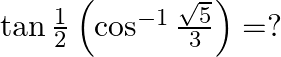
A. 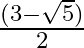
B. 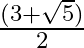
C. 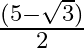
D. 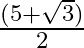
Solution: Option(A) is correct. To Find: The value of $\tan \frac{1}{2}\left(\cos ^{-1} \frac{\sqrt{5}}{3}\right)$ Let, $x=\cos ^{-1} \frac{\sqrt{5}}{3}$ $\Rightarrow \cos x=\frac{\sqrt{5}}{3}$ Now,...
Mark the tick against the correct answer in the following: ![Rendered by QuickLaTeX.com \tan \left[2 \tan ^{-1} \frac{1}{5}-\frac{\pi}{4}\right]=?](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7b682318a7b83adde969470e6e4ef16e_l3.png)
A. 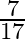
B. 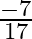
C. 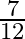
D. 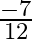
Solution: Option(B) is correct. To Find: The value of $\tan \left(2 \tan ^{-1} \frac{1}{5}-\frac{\pi}{4}\right)$ Consider, $\tan \left(2 \tan ^{-1} \frac{1}{5}-\frac{\pi}{4}\right)=\tan \left(\tan...
Mark the tick against the correct answer in the following: 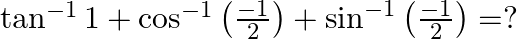
A. 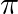
B. 
C. 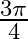
D. 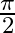
Solution: Option(B) is correct. To Find: The value of $\tan ^{-1} 1+\cos ^{-1}\left(\frac{-1}{2}\right)+\sin ^{-1}\left(\frac{-1}{2}\right)$ Now, let $x=\tan ^{-1} 1+\cos...
Mark the tick against the correct answer in the following: 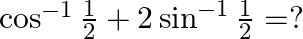
A. 
B. 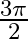
C. 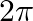
D. none of these
Solution: Option(A) is correct. To Find: The value of $\cos ^{-1} \frac{1}{2}+2 \sin ^{-1} \frac{1}{2}$ Now, let $x=\cos ^{-1} \frac{1}{2}+2 \sin ^{-1} \frac{1}{2}$ $\Rightarrow...
Mark the tick against the correct answer in the following: 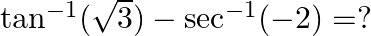
A. 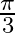
B. 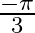
C. 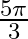
D. none of these
Solution: Option(B) is correct. To Find: The value of $\tan ^{-1}(\sqrt{3})-\sec ^{-1}(-2)$ Let, $x=\tan ^{-1}(\sqrt{3})-\sec ^{-1}(-2)$ $\begin{array}{l} \Rightarrow...
Mark the tick against the correct answer in the following: 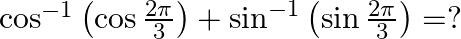
A. 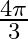
B. 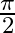
C. 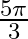
D. 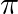
Solution: Option(D) is correct. To Find: The value of $\cos ^{-1}\left(\cos \left(\frac{2 \pi}{3}\right)\right)+\sin ^{-1}\left(\sin \left(\frac{2 \pi}{3}\right)\right)$ Here, consider $\cos...
Mark the tick against the correct answer in the following: The value of 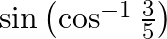 is
is
A. 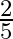
B. 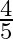
C. 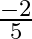
D. none of these
Solution: Option(B) is correct. To Find: The value of $\sin \left(\cos ^{-1} \frac{3}{5}\right)$ Now, let $x=\cos ^{-1} \frac{3}{5}$ $\Rightarrow \cos x=\frac{3}{5}$ Now , $\sin x=\sqrt{1-\cos ^{2}...
Mark the tick against the correct answer in the following: If 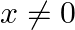 then
then 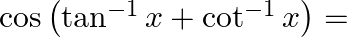 ?
?
A. 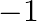
B. 1
C. 0
D. none of these
Solution: Option(C) is correct. Given: $x \neq 0$ To Find: The value of $\cos \left(\tan ^{-1} x+\cot ^{-1} x\right)$ Now, let $x=\cos \left(\tan ^{-1} x+\cot ^{-1} x\right)$ $\begin{array}{l}...
Mark the tick against the correct answer in the following: The value of 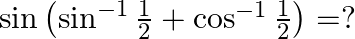
A. 0
B. 1
C. 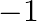
D. none of these
Solution: Option(1) is correct. To Find: The value of $\sin \left(\sin ^{-1} \frac{1}{2}+\cos ^{-1} \frac{1}{2}\right)$ Now, let $x=\sin \left(\sin ^{-1} \frac{1}{2}+\cos ^{-1} \frac{1}{2}\right)$...
Mark the tick against the correct answer in the following: 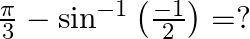
A. 0
B. 
C. 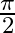
D. 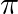
Solution: Option(D) is correct. To Find: The value of $\frac{\pi}{3}-\sin ^{-1}\left(\frac{-1}{2}\right)$ Now, let $x=\frac{\pi}{3}-\sin ^{-1}\left(\frac{-1}{2}\right)$ $\begin{array}{l} \Rightarrow...
Mark the tick against the correct answer in the following: The value of 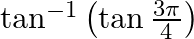 is
is
A. 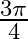
B. 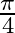
C. 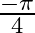
D. none of these
Solution: Option(C) is correct. To Find: The value of $\tan ^{-1}\left(\tan \left(\frac{3 \pi}{4}\right)\right)$ Now, let $x=\tan ^{-1}\left(\tan \left(\frac{3 \pi}{4}\right)\right)$ $\Rightarrow...
Mark the tick against the correct answer in the following: The value of 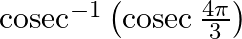 is
is
A. 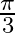
B. 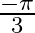
C. 
D. none of these
Solution: Option(B) is correct. To Find: The value of $\operatorname{cosec}^{-1}\left(\operatorname{cosec}\left(\frac{4 \pi}{3}\right)\right)$ Now, let...
Mark the tick against the correct answer in the following: The value of 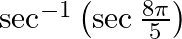 is
is
A. 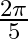
B. 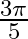
C. 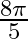
D. none of these
Solution: Option(A) is correct. To Find: The value of $\sec ^{-1}\left(\sec \left(\frac{8 \pi}{5}\right)\right)$ Now, let $x=\sec ^{-1}\left(\sec \left(\frac{8 \pi}{5}\right)\right)$ $\Rightarrow...
Mark the tick against the correct answer in the following: The value of 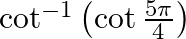 is
is
A. 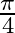
B. 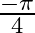
C. 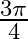
D. none of these
Solution: Option(A) is correct. To Find: The value of $\cot ^{-1}\left(\cot \left(\frac{5 \pi}{4}\right)\right)$ Now, let $x=\cot ^{-1}\left(\cot \left(\frac{5 \pi}{4}\right)\right)$ $\Rightarrow...
Mark the tick against the correct answer in the following: The value of 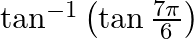 is
is
A. 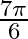
B. 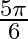
C. 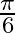
D. none of these
Solution: To Find: The value of $\tan ^{-1}\left(\tan \left(\frac{7 \pi}{6}\right)\right)$ Now, let $x=\tan ^{-1}\left(\tan \left(\frac{7 \pi}{6}\right)\right)$ $\Rightarrow \tan x=\tan...
Mark the tick against the correct answer in the following: The value of 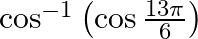 is A.
is A. 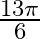 B.
B. 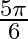 C.
C. 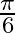 D.
D. 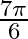
Solution: Option(C) ids correct. To Find: The value of $\cos ^{-1}\left(\cos \left(\frac{13 \pi}{6}\right)\right)$ Now, let $x=\cos ^{-1}\left(\cos \left(\frac{13 \pi}{6}\right)\right)$ $\Rightarrow...
Mark the tick against the correct answer in the following: The value of 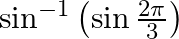 is
is
A. 
B. 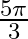
C. 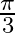
D. none of these
Solution: Option(C) us correct. To Find: The value of $\sin ^{-1}\left(\sin \left(\frac{2 \pi}{3}\right)\right)$ Now, let $x=\sin ^{-1}\left(\sin \left(\frac{2 \pi}{3}\right)\right)$ $\Rightarrow...
Mark the tick against the correct answer in the following: The principal value of 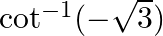 is
is
A. 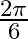
B. 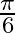
C. 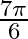
D. 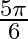
Solution: Option(D) is correct. To Find: The Principle value of $\cot ^{-1}(-\sqrt{3})$ Let the principle value be given by $\mathrm{x}$ Now, let $x=\cot ^{-1}(-\sqrt{3})$ $\begin{array}{l}...
Mark the tick against the correct answer in the following: The principal value of 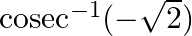 is
is
A. 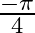
B. 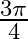
C. 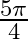
D. none of these
Solution: Option(A) is correct. To Find: The Principle value of $\operatorname{cosec}^{-1}(-\sqrt{2})$ Let the principle value be given by $\mathrm{x}$ Now, let...
Mark the tick against the correct answer in the following: The principal value of 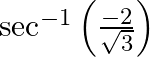 is
is
A. 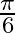
B. 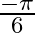
C. 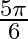
D. 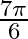
Solution: Option(C) is correct. To Find: The Principle value of $\sec ^{-1}\left(\frac{-2}{\sqrt{3}}\right)$ Let the principle value be given by $x$ Now, let $x=\sec...
Mark the tick against the correct answer in the following: The principal value of 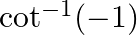 is
is
A. 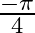
B. 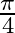
C. 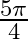
D. 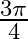
Solution: Option(D) is correct. To Find: The Principle value of $\cot ^{-1}(-1)$ Let the principle value be given by $x$ Now, let $x=\cot ^{-1}(-1)$ $\Rightarrow \cot x=-1$ $\Rightarrow \cot x=-\cot...
Mark the tick against the correct answer in the following: The principal value of 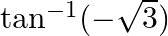 is
is
A. 
B. 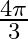
C. 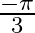
D. none of these
Solution: Option(C) is correct. To Find: The Principle value of $\tan ^{-1}(-\sqrt{3})$ Let the principle value be given by $x$ Now, let $x=\tan ^{-1}(-\sqrt{3})$ $\begin{array}{l} \Rightarrow \tan...
Mark the tick against the correct answer in the following: The principal value of 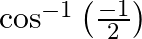 is
is
A. 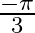
B. 
C. 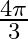
D. 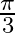
Solution: Option(B) is correct. To Find: The Principle value of $\cos ^{-1}\left(\frac{-1}{2}\right)$ Let the principle value be given by $x$ Now, let $x=\cos ^{-1}\left(\frac{-1}{2}\right)$...
Mark the tick against the correct answer in the following: The principal value of 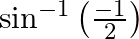 is
is
A. 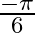
B. 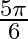
C. 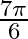
D. none of these
Solution: Option(A) is correct. To Find: The Principle value of $\sin ^{-1}\left(\frac{-1}{2}\right)$ Let the principle value be given by $x$ Now, let $x=\sin ^{-1}\left(\frac{-1}{2}\right)$...
Mark the tick against the correct answer in the following: The principal value of 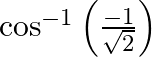 is
is
A. 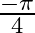
B. 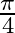
C. 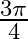
D. 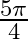
Solution: Option(C) is correct. To Find: The Principle value of $\cos ^{-1}\left(\frac{-1}{\sqrt{2}}\right)$ Let the principle value be given by $\mathrm{x}$ Now, let $x=\cos...
Mark the tick against the correct answer in the following: The principal value of 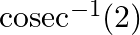 is
is
A. 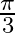
B. 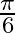
C. 
D. 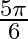
Solution: Option(B) is correct. To Find: The Principle value of $\operatorname{cosec}^{-1}(2)$ Let the principle value be given by $x$ Now, let $x=\operatorname{cosec}^{-1}(2)$ $\begin{array}{l}...
Mark the tick against the correct answer in the following: The principal value of 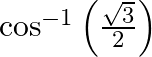 is
is
A. 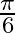
B. 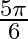
C. 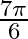
D. none of these
Solution: Option (A) is correct. To Find:The Principle value of $\cos ^{-1}\left(\frac{\sqrt{3}}{2}\right)$ Let the principle value be given by $x$ Now, let $x=\cos...
Write down the interval for the principal-value branch of each of the following functions and draw its graph: 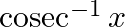
Solution: Principal value branch of $\operatorname{cosec}^{-1} x$ is $\left[-\frac{\pi}{2}, 0\right) \cup\left(0, \frac{\pi}{2}\right]$
Write down the interval for the principal-value branch of each of the following functions and draw its graph: 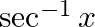
Solution: Principal value branch of $\sec ^{-1} x$ is $\left[0, \frac{\pi}{2}\right) \cup\left(\frac{\pi}{2}, \pi\right]$
Write down the interval for the principal-value branch of each of the following functions and draw its graph: 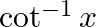
Solution: Principal value branch of $\cot ^{-1} x$ is $(0, \pi)$
Write down the interval for the principal-value branch of each of the following functions and draw its graph: 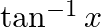
Solution: Principal value branch of $\tan ^{-1} \times$ is $\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$
Write down the interval for the principal-value branch of each of the following functions and draw its graph: 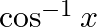
Solution: Principal value branch of $\cos ^{-1} x$ is $[0, \pi]$
Write down the interval for the principal-value branch of each of the following functions and draw its graph: 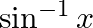
Solution: Principal value branch of $\sin ^{-1} x$ is $\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$
Solve for  :
: 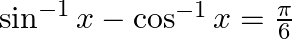
Solution: Given: $\sin ^{-1} x-\cos ^{-1} x=\frac{\pi}{6}$ We know that $\sin ^{-1} \mathrm{x}+\cos ^{-1} \mathrm{x}=\frac{\pi}{2}$ So, $\sin ^{-1} x=\frac{\pi}{2}-\cos ^{-1} x$ Substituting in the...
Solve for  :
: 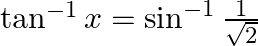
Solution: To find: value of $x$ Given: $\tan ^{-1} \mathrm{x}=\sin ^{-1} \frac{1}{\sqrt{2}}$ We know that $\sin \frac{\pi}{4}=\frac{1}{\sqrt{2}}$ Therefore, $\frac{\pi}{4}=\sin ^{-1}...
Solve for  :
: 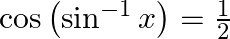
Solution: To find: value of $x$ Given: $\cos \left(\sin ^{-1} \mathrm{x}\right)=\frac{1}{2}$ $\text { LHS }=\cos \left(\sin ^{-1} x\right)$ $\begin{array}{l} =\cos \left(\cos...
Solve for  :
: 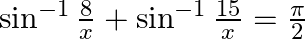
Solution: To find: value of $x$ Given: $\sin ^{-1} \frac{\mathrm{g}}{\mathrm{x}}+\sin ^{-1} \frac{15}{\mathrm{x}}=\frac{\pi}{2}$ We know $\sin ^{-1} \mathrm{x}+\cos ^{-1} \mathrm{x}=\frac{\pi}{2}$...
Solve for  :
: 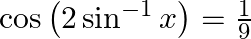
Solution: To find: value of $x$ Formula Used: $2 \sin ^{-1} x=\sin ^{-1}\left(2 x \sqrt{1-x^{2}}\right)$. Given: $\cos \left(2 \sin ^{-1} x\right)=\frac{1}{9}$ $\text { LHS }=\cos \left(2 \sin ^{-1}...
Solve for 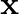 :
: 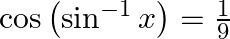
Solution: To find: value of $x$ Given: $\cos \left(\sin ^{-1} x\right)=\frac{1}{9}$ $\mathrm{LHS}=\cos \left(\sin ^{-1} \mathrm{x}\right) \ldots(1)$ Let $\sin \theta=x$ Therefore $\theta=\sin ^{-1}...
Solve for x: 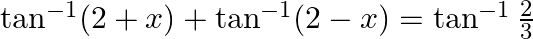
Solution: To find: value of $x$ Formula Used: $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$ where xy $<1$ Given: $\tan ^{-1}(2+x)+\tan ^{-1}(2-x)=\tan ^{-1} \frac{2}{3}$...
Solve for  :
: 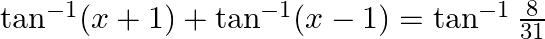
Solution: To find: value of $x$ Formula Used: $\tan ^{-1} \mathrm{x}+\tan ^{-1} \mathrm{y}=\tan ^{-1}\left(\frac{\mathrm{x}+y}{1-\mathrm{xy}}\right)$ where $\mathrm{xy}<1$ Given: $\tan...
Prove that: 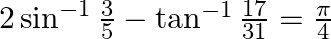
Solution: To Prove: $2 \sin ^{-1} \frac{3}{5}-\tan ^{-1} \frac{17}{31}=\frac{\pi}{4}$ Formula Used: 1) $2 \sin ^{-1} x=\sin ^{-1}\left(2 x \times \sqrt{1-x^{2}}\right)$ 2) $\tan ^{-1}...
Prove that: 
Solution: To Prove: $\sin ^{-1} \frac{1}{\sqrt{17}}+\cos ^{-1} \frac{9}{\sqrt{85}}=\tan ^{-1} \frac{1}{2}$ Formula Used: $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$ where $x...
Prove that: 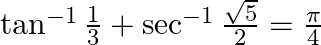
Solution: To Prove: $\tan ^{-1} \frac{1}{3}+\sec ^{-1} \frac{\sqrt{5}}{2}=\frac{\pi}{4}$ Formula Used: $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$ where $x y<1$ Proof:...
Prove that: 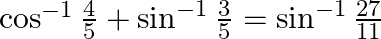
Solution: To Prove: $\cos ^{-1} \frac{4}{5}+\sin ^{-1} \frac{3}{5}=\sin ^{-1} \frac{27}{11}$ Formula Used: $\sin ^{-1} x+\sin ^{-1} y=\sin ^{-1}\left(x \times \sqrt{1-y^{2}}+y \times...
Prove that: 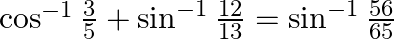
Solution: To Prove: $\cos ^{-1} \frac{3}{5}+\sin ^{-1} \frac{12}{13}=\sin ^{-1} \frac{56}{65}$ Formula Used: $\sin ^{-1} \mathrm{x}+\sin ^{-1} \mathrm{y}=\sin ^{-1}\left(\mathrm{x} \times...
Prove that: 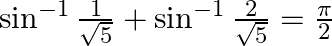
Solution: To Prove: $\sin ^{-1} \frac{1}{\sqrt{5}}+\sin ^{-1} \frac{2}{\sqrt{5}}=\frac{\pi}{2}$ Formula Used: $\sin ^{-1} \mathrm{x}+\sin ^{-1} \mathrm{y}=\sin ^{-1}\left(\mathrm{x} \times...
Prove that: 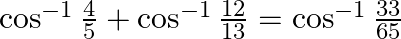
Solution: To Prove: $\cos ^{-1} \frac{4}{5}+\cos ^{-1} \frac{12}{13}=\cos ^{-1} \frac{33}{65}$ Formula Used: $\cos ^{-1} x+\cos ^{-1} y=\cos ^{-1}\left(x y-\sqrt{1-x^{2}} \times...
Prove that: 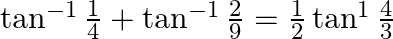
Solution: To Prove: $\tan ^{-1} \frac{1}{4}+\tan ^{-1} \frac{2}{9}=\frac{1}{2} \tan ^{-1} \frac{4}{3} \Rightarrow 2\left(\tan ^{-1} \frac{1}{4}+\tan ^{-1} \frac{2}{9}\right)=\tan ^{-1} \frac{4}{3}$...
Prove that: 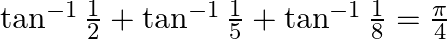
Solution: To Prove: $\tan ^{-1} \frac{1}{2}+\tan ^{-1} \frac{1}{5}+\tan ^{-1} \frac{1}{8}=\frac{\pi}{4}$ Formula Used: $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$ where $x...
Prove that: 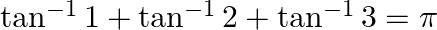
Solution: To Prove: $\tan ^{-1} 1+\tan ^{-1} 2+\tan ^{-1} 3=\pi$ Formula Used: $\tan ^{-1} \mathrm{x}+\tan ^{-1} \mathrm{y}=\pi+\tan ^{-1}\left(\frac{\mathrm{x}+\mathrm{y}}{1-\mathrm{xy}}\right)$...
Prove that: 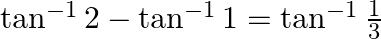
Solution: To Prove: $\tan ^{-1} 2-\tan ^{-1} 1=\tan ^{-1} \frac{1}{3}$ Formula Used: $\tan ^{-1} \mathrm{x}-\tan ^{-1} \mathrm{y}=\tan ^{-1}\left(\frac{\mathrm{x}-\mathrm{y}}{1+\mathrm{xy}}\right)$...
Prove that: 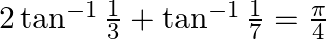
Solution: To Prove: $2 \tan ^{-1} \frac{1}{3}+\tan ^{-1} \frac{1}{7}=\frac{\pi}{4}$ Formula Used: $\tan ^{-1} \mathrm{x}+\tan ^{-1} \mathrm{y}=\tan...
Prove that: 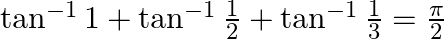
Solution: To Prove: $\tan ^{-1} 1+\tan ^{-1} \frac{1}{2}+\tan ^{-1} \frac{1}{3}=\frac{\pi}{2}$ Formula Used: $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$ Proof:...
Prove that: 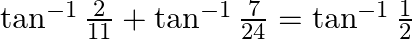
Solution: To Prove: $\tan ^{-1} \frac{2}{11}+\tan ^{-1} \frac{7}{24}=\tan ^{-1} \frac{1}{2}$ Formula Used: $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$ Proof:...
Prove that: 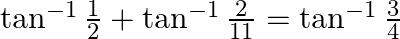
Solution: To Prove: $\tan ^{-1} \frac{1}{2}+\tan ^{-1} \frac{2}{11}=\tan ^{-1} \frac{3}{4}$ Formula Used: $\tan ^{-1} \mathrm{x}+\tan ^{-1} \mathrm{y}=\tan...
Prove that: 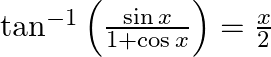
Solution: To Prove: $\tan ^{-1}\left(\frac{\sin x}{1+\cos x}\right)=\frac{x}{2}$ Formula Used: 1) $\sin A=2 \times \sin \frac{A}{2} \times \cos \frac{A}{2}$ 2) $1+\cos A=2 \cos ^{2} \frac{A}{2}$...
Prove that: 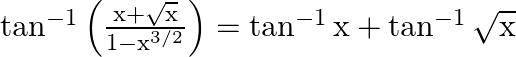
Solution: We know that, $\tan ^{-1}\left(\frac{A+B}{1-A B}\right)=\tan ^{-1} A+\tan ^{-1} B$ Now, taking $A=x$ and $B=\sqrt{x}$ We get, $\tan ^{-1} x+\tan ^{-1} \sqrt{x}=\tan...
Prove that: 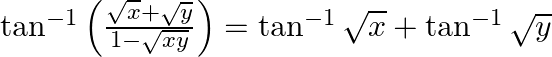
Solution: To Prove: $\tan ^{-1}\left(\frac{\sqrt{x}+\sqrt{y}}{1-\sqrt{x y}}\right)=\tan ^{-1} \sqrt{x}+\tan ^{-1} \sqrt{y}$ We know that, $\tan A+\tan B=\frac{\tan A+\tan B}{1-\tan A \tan B}$ Also,...
Prove that: 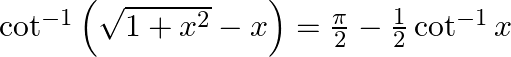
Solution: To Prove: $\cot ^{-1}\left(\sqrt{1+x^{2}}-x\right)=\frac{\pi}{2}-\frac{1}{2} \cot ^{-1} x$ Formula Used: 1) $\tan \left(\frac{\pi}{4}+A\right)=\frac{1+\tan A}{1-\tan A}$ 2)...
Prove that: 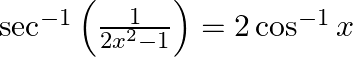
Solution: To Prove: $\sec ^{-1}\left(\frac{1}{2 x^{2}-1}\right)=2 \cos ^{-1} x$ Formula Used: 1) $\cos 2 A=2 \cos ^{2} A-1$ 2) $\cos ^{-1} A=\sec ^{-1}\left(\frac{1}{A}\right)$ Proof:...
Prove that: 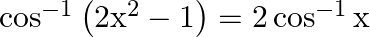
Solution: To Prove: $\cos ^{-1}\left(2 x^{2}-1\right)=2 \cos ^{-1} x$ Formula Used: $\cos 2 A=2 \cos ^{2} A-1$ Proof: $\text { LHS }=\cos ^{-1}\left(2 x^{2}-1\right) \ldots(1)$ Let $x=\cos A \ldots$...
Prove that: 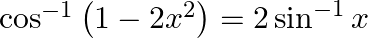
Solution: To Prove: $\cos ^{-1}\left(1-2 x^{2}\right)=2 \sin ^{-1} x$ Formula Used: $\cos 2 A=1-2 \sin ^{2} A$ Proof: $\operatorname{LHS}=\cos ^{-1}\left(1-2 x^{2}\right) \ldots(1)$ Let $x=\sin A...
Prove that: 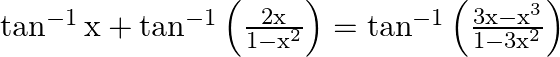
Solution: To Prove: $\tan ^{-1} x+\tan ^{-1}\left(\frac{2 x}{1-x^{2}}\right)=\tan ^{-1}\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right)$ Formula Used: $\tan ^{-1} x+\tan ^{-1} y=\tan...
Prove that: 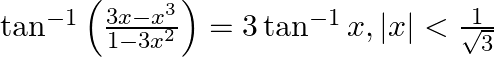
Solution: To Prove: $\tan ^{-1}\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right)=3 \tan ^{-1} x$ Formula Used: $\tan 3 A=\frac{3 \tan A-\tan ^{3} A}{1-3 \tan ^{2} A}$ Proof: $\text { LHS }=\tan...
Prove that: 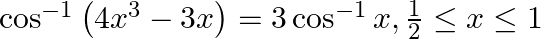
Solution: To Prove: $\cos ^{-1}\left(4 x^{3}-3 x\right)=3 \cos ^{-1} x$ Formula Used: $\cos 3 A=4 \cos ^{3} A-3 \cos A$ Proof: $\text { LHS }=\cos ^{-1}\left(4 x^{3}-3 x\right) \ldots(1)$ Let...
Prove that: 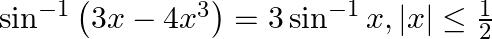
Solution: To Prove: $\sin ^{-1}\left(3 x-4 x^{3}\right)=3 \sin ^{-1} x$ Formula Used: $\sin 3 \mathrm{~A}=3 \sin \mathrm{A}-4 \sin ^{3} \mathrm{~A}$ Proof: $\operatorname{LHS}=\sin ^{-1}\left(3 x-4...
Prove that: 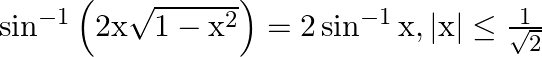
Solution: To Prove: $\sin ^{-1}\left(2 x \sqrt{1-x^{2}}\right)=2 \sin ^{-1} x$ Formula Used: $\sin 2 A=2 \times \sin A \times \cos A$ Proof: $\text { LHS }=\sin ^{-1}\left(2 x \sqrt{1-x^{2}}\right)...
Prove that: 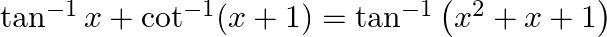
Solution: To Prove: $\tan ^{-1} x+\cot ^{-1}(x+1)=\tan ^{-1}\left(x^{2}+x+1\right)$ Formula Used: 1) $\cot ^{-1} \mathrm{x}=\tan ^{-1} \frac{1}{\mathrm{x}}$ 2) $\tan ^{-1} \mathrm{x}+\tan ^{-1}...
Prove that: 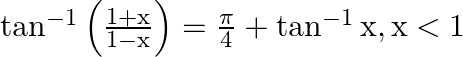
Solution: To Prove: $\tan ^{-1}\left(\frac{1+x}{1-x}\right)=\frac{\pi}{4}+\tan ^{-1} x$ Formula Used: $\tan \left(\frac{\pi}{4}+A\right)=\frac{1+\tan A}{1-\tan A}$ Proof: $\mathrm{LHS}=\tan...
Find the principal value of each of the following: 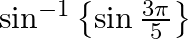
Solution: $\begin{array}{l} \sin ^{-1}\left\{\sin \left(\frac{3 \pi}{5}\right)\right\} \\ =\sin ^{-1}\left\{\sin \left(\pi-\frac{2 \pi}{5}\right)\right\} \end{array}$ [Formula: $\sin (\pi-x)=\sin...
Find the principal value of each of the following : 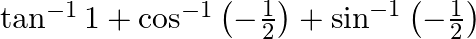
Solution: [Formula: $\cos ^{-1}(-x)=\pi-\cos (x)$ and $\left.\sin ^{-1}(-x)=-\sin (x)\right]$ $\tan ^{-1} 1+\left(\pi-\cos ^{-1}\left(\frac{1}{2}\right)\right)+\left(-\sin...
Find the principal value of each of the following : 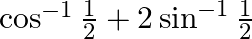
Solution: Putting the values of the inverse trigonometric terms $\begin{array}{l} \frac{\pi}{3}+2 \times \frac{\pi}{6} \\ =\frac{\pi}{3}+\frac{\pi}{3} \\ =\frac{2 \pi}{3} \end{array}$
Find the principal value of each of the following : 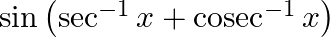
Solution: $\sin \left(\sec ^{-1} x+\operatorname{cosec}^{-1} x\right)=\sin \left(\frac{\pi}{2}\right)$ [Formula: $\left.\sec ^{-1} x+\operatorname{cosec}^{-1} x=\frac{\pi}{2}\right]$ Putting the...
Find the principal value of each of the following : 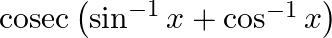
Solution: $\operatorname{cosec}\left(\sin ^{-1} x+\cos ^{-1} x\right)=\operatorname{cosec} \frac{\pi}{2}\left[\right.$ Formula: $\left.\sin ^{-1} x+\cos ^{-1} x=\frac{\pi}{2}\right]$ Putting the...
Find the principal value of each of the following: 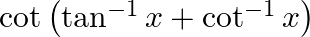
Solution: $\cot \left(\tan ^{-1} x+\cot ^{-1} x\right)=\cot \left(\frac{\pi}{2}\right)$ [Formula: $\left.\tan ^{-1} x+\cot ^{-1} x=\frac{\pi}{2}\right]$ Putting value of $\cot...
Find the principal value of each of the following : 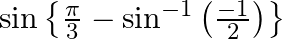
Solution: $\begin{array}{l} \sin \left\{\frac{\pi}{3}-\sin ^{-1}\left(\frac{-1}{2}\right)\right\}\left[\text { Formula: } \sin ^{-1}(-\mathrm{x})=-\sin ^{-1} \mathrm{x}\right] \\ =\sin...
Find the principal value of each of the following : 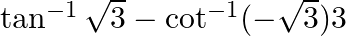
Solution: $\tan ^{-1} \sqrt{3}-\cot ^{-1}(-\sqrt{3})$ Putting the value of $\tan ^{-1} \sqrt{3}$ and using the formula $\begin{array}{l} \cot ^{-1}(-x)=\pi-\cot ^{-1} x \\...
Find the principal value of each of the following : 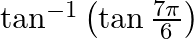
Solution: $\tan ^{-1}\left(\tan \frac{7 \pi}{6}\right)=\tan ^{-1}\left(\tan \left(\pi+\frac{\pi}{6}\right)\right)$ [ Formula: $\tan (\pi+x)=\tan x$, as tan is positive in the third quadrant.] $=\tan...
Find the principal value of each of the following : 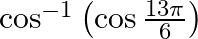
Solution: $\cos ^{-1}\left(\cos \frac{13 \pi}{6}\right)=\cos ^{-1}\left(\cos \left(2 \pi+\frac{\pi}{6}\right)\right)$ [ Formula: $\cos (2 \pi+x)=\cos x, \cos$ is positive in the first quadrant. ]...
Find the principal value of each of the following : 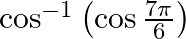
Solution: $\cos ^{-1}\left(\cos \frac{7 \pi}{6}\right)=\cos ^{-1}\left(\cos \left(2 \pi-\frac{5 \pi}{6}\right)\right)$ [Formula: $\cos (2 \pi-x)=\cos (x)$, as cos has a positive vaule in the fourth...
Find the principal value of each of the following : 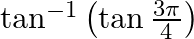
Solution: $\tan ^{-1}\left(\tan \frac{3 \pi}{4}\right)=\tan ^{-1}\left(\tan \left(\pi-\frac{\pi}{4}\right)\right)$ [Formula: $\tan (\pi-x)=-\tan (x)$, as tan is negative in the second quadrant. ]...
Find the principal value of each of the following : 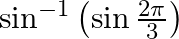
Solution: $\sin ^{-1}\left(\sin \frac{2 \pi}{3}\right)=\sin ^{-1}\left(\sin \left(\pi-\frac{\pi}{3}\right)\right)$ [ Formula: $\sin (\pi-x)=\sin x)$ $=\sin ^{-1}\left(\sin \frac{\pi}{3}\right)$ [...
Find the principal value of each of the following : 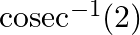
Solution: $\operatorname{cosec}^{-1}(2)$ Putting the value directly $=\frac{\pi}{6}$
Find the principal value of each of the following : 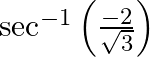
Solution: $\sec ^{-1}\left(\frac{-2}{\sqrt{3}}\right)=\pi-\sec ^{-1}\left(\frac{2}{\sqrt{3}}\right)\left[\right.$ Formula: $\left.\sec ^{-1}(-x)=\pi-\sec ^{-1}(x)\right]$ $\begin{array}{l}...
Find the principal value of each of the following : 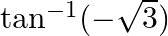
Solution: $\tan ^{-1}(-\sqrt{3})=-\tan ^{-1}(\sqrt{3})$ [Formula: $\left.\tan ^{-1}(-x)=-\tan ^{-1}(x)\right]$ $=-\frac{\pi}{3}$
Find the principal value of each of the following : 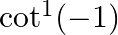
Solution: $\cot ^{-1}(-1)=\pi-\cot ^{-1}(1)$ [Formula: $\left.\cot ^{-1}(-x)=\pi-\cot ^{-1}(x)\right]$ $\begin{array}{l} =\pi-\frac{\pi}{4} \\ =\frac{3 \pi}{4} \end{array}$
Find the principal value of each of the following : 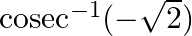
Solution: $\operatorname{cosec}^{-1}(-\sqrt{2})=-\operatorname{cosec}^{-1}(\sqrt{2})$ [Formula: $\left.\operatorname{cosec}^{-1}(-x)=-\operatorname{cosec}^{-1}(x)\right]$ $=-\frac{\pi}{4}$ This can...
Find the principal value of each of the following : 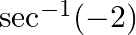
Solution: $\sec ^{-1}(-2)=\pi-\sec ^{-1}(2)\left[\right.$ Formula: $\left.\sec ^{-1}(-x)=\pi-\sec ^{-1}(x)\right]$ $\begin{array}{l} =\pi-\frac{\pi}{3} \\ =\frac{2 \pi}{3} \end{array}$
Find the principal value of each of the following : 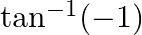
Solution: $\tan (-1)=-\tan (1)\left[\right.$ Formula: $\left.\tan ^{-1}(-x)=-\tan ^{-1}(x)\right]$ [ We know that $\tan \frac{\pi}{4}=1$, thus $\left.\tan ^{-1} \frac{\pi}{4}=1\right]$...
Find the principal value of each of the following : 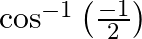
Solution: $\cos ^{-1}\left(\frac{-1}{2}\right)=\pi-\cos ^{-1}\left(\frac{1}{2}\right)$ [ Formula: $\left.\cos ^{-1}(-x)=-\cos ^{-1}(x)\right]$ $=\pi-\frac{\pi}{3}$ $=\frac{2 \pi}{3}$
Find the principal value of each of the following : 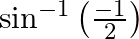
Solution: $\sin ^{-1}\left(\frac{-1}{2}\right)=-\sin ^{-1}\left(\frac{1}{2}\right)\left[\right.$ Formula: $\left.\sin ^{-1}(-x)=\sin ^{-1}(x)\right]$ $=-\frac{\pi}{6}$
Evaluate 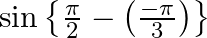
$\begin{array}{l} \sin \left(\frac{\pi}{2}+\frac{\pi}{3}\right) \\ =\sin \left(\frac{5 \pi}{6}\right) \\ =\sin \left(\pi-\frac{\pi}{6}\right) \\ =\sin \frac{\pi}{6} \\ =\frac{1}{2} \end{array}$
Evaluate 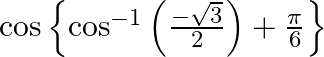
$\cos \left\{\pi-\frac{\pi}{6}+\frac{\pi}{6}\right\}$ $\begin{array}{l} =\cos \{\pi\} \\ =\cos \left(\frac{\pi}{2}+\frac{\pi}{2}\right) \\ =-1 \end{array}$
Find the principal value of : (v) 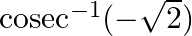 (vi)
(vi) 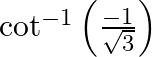
(v) Let $\operatorname{cosec}^{-1}(-\sqrt{2})=x$ $\begin{array}{l} \Rightarrow-\operatorname{cosec}^{-1}(\sqrt{2})=x\left[\text { Formula: }...
Find the principal value of : (iii) 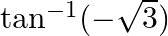 (iv)
(iv) 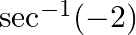
(iii) Let $\tan ^{-1}(-\sqrt{3})=x$ $\Rightarrow-\tan ^{-1}(\sqrt{3})=x\left[\right.$ Formula: $\left.\tan ^{-1}(-x)=-\tan ^{-1}(x)\right]$ $\Rightarrow \sqrt{3}=-\tan x$ $\therefore...
Find the principal value of : (i) 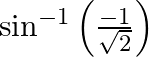 (ii)
(ii) 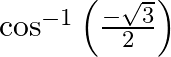
(i) Let $\sin ^{-1}\left(\frac{-1}{\sqrt{2}}\right)=x$ $\Rightarrow-\sin ^{-1}\left(\frac{1}{\sqrt{2}}\right)=x\left[\right.$ Formula: $\left.\sin ^{-1}(-x)=-\sin ^{-1} x\right]$ $\Rightarrow...
Find the principal value of : (vii) 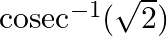
(vii) Let $\operatorname{cosec}^{-1}(\sqrt{2})=x$ $\Rightarrow \sqrt{2}=\operatorname{cosec} x$ $\therefore \mathrm{x}=\frac{\pi}{4}$
Find the principal value of : (v) 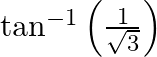 (vi)
(vi) 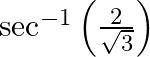
(v) Let $\tan ^{-1}\left(\frac{1}{\sqrt{3}}\right)=x$ $\Rightarrow \frac{1}{\sqrt{3}}=\tan \mathrm{x}$ [We know which value of $\mathrm{x}$ $\therefore \mathrm{x}=\frac{\pi}{6}$ (vi) Let $\sec...
Find the principal value of : (iii) 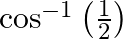 (iv)
(iv) 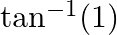
(iii) Let $\cos ^{-1}\left(\frac{1}{2}\right)=x$ $\Rightarrow \frac{1}{2}=\cos x$ [We know which value of $x$ when put in this expression will give us this result] $\therefore...
Find the principal value of : (i) 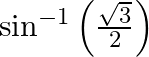 (ii)
(ii) 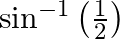
(i) Let $\sin ^{-1}\left(\frac{\sqrt{3}}{2}\right)=x$ $\Rightarrow \frac{\sqrt{3}}{2}=\sin x$ => $\therefore \mathrm{x}=\frac{\pi}{3}$ (ii) Let $\sin ^{-1}\left(\frac{1}{2}\right)=x$ $\Rightarrow...
