Solution: $\begin{array}{l} \sin ^{-1}\left\{\sin \left(\frac{3 \pi}{5}\right)\right\} \\ =\sin ^{-1}\left\{\sin \left(\pi-\frac{2 \pi}{5}\right)\right\} \end{array}$ [Formula: $\sin (\pi-x)=\sin...
Find the principal value of each of the following:
Find the principal value of each of the following : 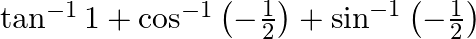
Solution: [Formula: $\cos ^{-1}(-x)=\pi-\cos (x)$ and $\left.\sin ^{-1}(-x)=-\sin (x)\right]$ $\tan ^{-1} 1+\left(\pi-\cos ^{-1}\left(\frac{1}{2}\right)\right)+\left(-\sin...
Find the principal value of each of the following : 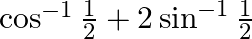
Solution: Putting the values of the inverse trigonometric terms $\begin{array}{l} \frac{\pi}{3}+2 \times \frac{\pi}{6} \\ =\frac{\pi}{3}+\frac{\pi}{3} \\ =\frac{2 \pi}{3} \end{array}$
Find the principal value of each of the following : 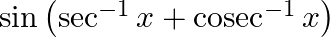
Solution: $\sin \left(\sec ^{-1} x+\operatorname{cosec}^{-1} x\right)=\sin \left(\frac{\pi}{2}\right)$ [Formula: $\left.\sec ^{-1} x+\operatorname{cosec}^{-1} x=\frac{\pi}{2}\right]$ Putting the...
Find the principal value of each of the following : 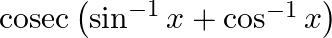
Solution: $\operatorname{cosec}\left(\sin ^{-1} x+\cos ^{-1} x\right)=\operatorname{cosec} \frac{\pi}{2}\left[\right.$ Formula: $\left.\sin ^{-1} x+\cos ^{-1} x=\frac{\pi}{2}\right]$ Putting the...
Find the principal value of each of the following: 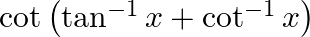
Solution: $\cot \left(\tan ^{-1} x+\cot ^{-1} x\right)=\cot \left(\frac{\pi}{2}\right)$ [Formula: $\left.\tan ^{-1} x+\cot ^{-1} x=\frac{\pi}{2}\right]$ Putting value of $\cot...
Find the principal value of each of the following : 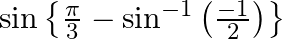
Solution: $\begin{array}{l} \sin \left\{\frac{\pi}{3}-\sin ^{-1}\left(\frac{-1}{2}\right)\right\}\left[\text { Formula: } \sin ^{-1}(-\mathrm{x})=-\sin ^{-1} \mathrm{x}\right] \\ =\sin...
Find the principal value of each of the following : 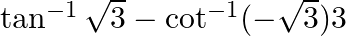
Solution: $\tan ^{-1} \sqrt{3}-\cot ^{-1}(-\sqrt{3})$ Putting the value of $\tan ^{-1} \sqrt{3}$ and using the formula $\begin{array}{l} \cot ^{-1}(-x)=\pi-\cot ^{-1} x \\...
Find the principal value of each of the following : 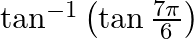
Solution: $\tan ^{-1}\left(\tan \frac{7 \pi}{6}\right)=\tan ^{-1}\left(\tan \left(\pi+\frac{\pi}{6}\right)\right)$ [ Formula: $\tan (\pi+x)=\tan x$, as tan is positive in the third quadrant.] $=\tan...
Find the principal value of each of the following : 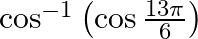
Solution: $\cos ^{-1}\left(\cos \frac{13 \pi}{6}\right)=\cos ^{-1}\left(\cos \left(2 \pi+\frac{\pi}{6}\right)\right)$ [ Formula: $\cos (2 \pi+x)=\cos x, \cos$ is positive in the first quadrant. ]...
Find the principal value of each of the following : 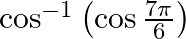
Solution: $\cos ^{-1}\left(\cos \frac{7 \pi}{6}\right)=\cos ^{-1}\left(\cos \left(2 \pi-\frac{5 \pi}{6}\right)\right)$ [Formula: $\cos (2 \pi-x)=\cos (x)$, as cos has a positive vaule in the fourth...
Find the principal value of each of the following : 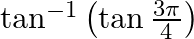
Solution: $\tan ^{-1}\left(\tan \frac{3 \pi}{4}\right)=\tan ^{-1}\left(\tan \left(\pi-\frac{\pi}{4}\right)\right)$ [Formula: $\tan (\pi-x)=-\tan (x)$, as tan is negative in the second quadrant. ]...
Find the principal value of each of the following : 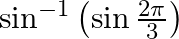
Solution: $\sin ^{-1}\left(\sin \frac{2 \pi}{3}\right)=\sin ^{-1}\left(\sin \left(\pi-\frac{\pi}{3}\right)\right)$ [ Formula: $\sin (\pi-x)=\sin x)$ $=\sin ^{-1}\left(\sin \frac{\pi}{3}\right)$ [...
Find the principal value of each of the following : 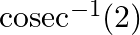
Solution: $\operatorname{cosec}^{-1}(2)$ Putting the value directly $=\frac{\pi}{6}$
Find the principal value of each of the following : 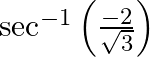
Solution: $\sec ^{-1}\left(\frac{-2}{\sqrt{3}}\right)=\pi-\sec ^{-1}\left(\frac{2}{\sqrt{3}}\right)\left[\right.$ Formula: $\left.\sec ^{-1}(-x)=\pi-\sec ^{-1}(x)\right]$ $\begin{array}{l}...
Find the principal value of each of the following : 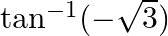
Solution: $\tan ^{-1}(-\sqrt{3})=-\tan ^{-1}(\sqrt{3})$ [Formula: $\left.\tan ^{-1}(-x)=-\tan ^{-1}(x)\right]$ $=-\frac{\pi}{3}$
Find the principal value of each of the following : 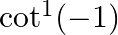
Solution: $\cot ^{-1}(-1)=\pi-\cot ^{-1}(1)$ [Formula: $\left.\cot ^{-1}(-x)=\pi-\cot ^{-1}(x)\right]$ $\begin{array}{l} =\pi-\frac{\pi}{4} \\ =\frac{3 \pi}{4} \end{array}$
Find the principal value of each of the following : 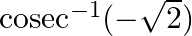
Solution: $\operatorname{cosec}^{-1}(-\sqrt{2})=-\operatorname{cosec}^{-1}(\sqrt{2})$ [Formula: $\left.\operatorname{cosec}^{-1}(-x)=-\operatorname{cosec}^{-1}(x)\right]$ $=-\frac{\pi}{4}$ This can...
Find the principal value of each of the following : 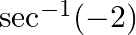
Solution: $\sec ^{-1}(-2)=\pi-\sec ^{-1}(2)\left[\right.$ Formula: $\left.\sec ^{-1}(-x)=\pi-\sec ^{-1}(x)\right]$ $\begin{array}{l} =\pi-\frac{\pi}{3} \\ =\frac{2 \pi}{3} \end{array}$
Find the principal value of each of the following : 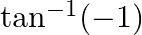
Solution: $\tan (-1)=-\tan (1)\left[\right.$ Formula: $\left.\tan ^{-1}(-x)=-\tan ^{-1}(x)\right]$ [ We know that $\tan \frac{\pi}{4}=1$, thus $\left.\tan ^{-1} \frac{\pi}{4}=1\right]$...
Find the principal value of each of the following : 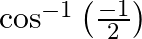
Solution: $\cos ^{-1}\left(\frac{-1}{2}\right)=\pi-\cos ^{-1}\left(\frac{1}{2}\right)$ [ Formula: $\left.\cos ^{-1}(-x)=-\cos ^{-1}(x)\right]$ $=\pi-\frac{\pi}{3}$ $=\frac{2 \pi}{3}$
Find the principal value of each of the following : 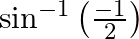
Solution: $\sin ^{-1}\left(\frac{-1}{2}\right)=-\sin ^{-1}\left(\frac{1}{2}\right)\left[\right.$ Formula: $\left.\sin ^{-1}(-x)=\sin ^{-1}(x)\right]$ $=-\frac{\pi}{6}$
