i) Time taken by the ray to travel from S to P1 is = t1 = √u2 + b2/c Time taken by the ray to travel from P1 to O is = t2 = v/c (1+ ½ b2/v2) Time taken to travel through the lens is =...
(i) Consider a thin lens placed between a source (S) and an observer (O). Let the thickness of the lens vary as 2 0 () – α = b wb w, where b is the verticle distance from the pole. w0 is a constant. Using Fermat’s principle i.e. the time of transit for a ray between the source and observer is an extremum, find the condition that all paraxial rays starting from the source will converge at a point O on the axis. Find the focal length.
Show that for a material with refractive index µ ≥ 2 , light incident at any angle shall be guided along a length perpendicular to the incident face. Answer:
Let the refractive index of the rectangular slab be μ ≥ √2. μ = 1/sin ic sin ic > 1/ μ cos r ≥ 1/ μ sin i/sin r = μ From Snell’s law Sin I = μ sin r i = 90o 1 + 1 ≤ μ2 2 ≤ μ2 Taking the square...
A jar of height h is filled with a transparent liquid of refractive index µ. At the centre of the jar on the bottom surface is a dot. Find the minimum diameter of a disc, such that when placed on the top surface symmetrically about the centre, the dot is invisible.
tan ic d/2/h ic = d/2h d = 2h tan ic d = 2h ×1/√μ2 – 1
A short object of length L is placed along the principal axis of a concave mirror away from focus. The object distance is u. If the mirror has a focal length f, what will be the length of the image? You may take L << |v-f|
The mirror formula is 1/v + 1/u = 1/f u is the object distance v is the image distance du = |u1 – u2| = L Differentiating on the both sides we get, dv/v2 = -du/u2 v/u = f/u-f du = L, therefore,...
For a glass prism (µ = √3 ) the angle of minimum deviation is equal to the angle of the prism. Find the angle of the prism.
μ = sin[(A + δm)/2]/sin (A/2)
Three immiscible liquids of densities d1 > d2 > d3 and refractive indices µ1 > µ2 > µ3 are put in a beaker. The height of each liquid column is h/3. A dot is made at the bottom of the beaker. For near-normal vision, find the apparent depth of the dot. Answer:
An unsymmetrical double convex thin lens forms the image of a point object on its axis. Will the position of the image change if the lens is reversed?
The near vision of an average person is 25cm. To view an object with an angular magnification of 10, what should be the power of the microscope?
Will the focal length of a lens for red light be more, same or less than that for blue light?
An astronomical refractive telescope has an objective of focal length 20m and an eyepiece of focal length 2cm.(a) The length of the telescope tube is 20.02m. (b) The magnification is 1000. (c) The image formed is inverted. (d) An objective of a larger aperture will increase the brightness and reduce chromatic aberration of the image.
Answer: (a) The length of the telescope tube is 20.02m. (b) The magnification is 1000. (c) The image formed is inverted. ...
A magnifying glass is used, as the object to be viewed can be brought closer to the eye than the normal near point. This results in
(a) a larger angle to be subtended by the object at the eye and hence viewed in greater detail.
(b) the formation of a virtual erect image.
(c) increase in the field of view.
(d) infinite magnification at the near point.
Answer: (a) a larger angle to be subtended by the object at the eye and hence viewed in greater detail. (b) the formation of a virtual erect image. ...
Between the primary and secondary rainbows, there is a dark band known as Alexandar’s dark band. This is because
(a) light scattered into this region interfere destructively.
(b) there is no light scattered into this region
(c) light is absorbed in this region.
(d) angle made at the eye by the scattered rays with respect to the incident light of the sun lies between approximately 42° and 50°.
Answer: (a) light scattered into this region interfere destructively. (d) angle made at the eye by the scattered rays with respect to the incident light of the sun lies between approximately 42° and...
A rectangular block of glass ABCD has a refractive index 1.6. A pin is placed midway on the face AB. When observed from the face AD, the pin shall
(a) appear to be near A.
(b) appear to be near D.
(c) appear to be at the centre of AD.
(d) not be seen at all.
Answer: (a) appear to be near A. (d) not be seen at all. The pin will appear to be near A as long as the angle of incidence on AD of the ray emerging from the pin is smaller...
Consider an extended object immersed in water contained in a plane trough. When seen from close to the edge of the trough the object looks distorted because
(a) the apparent depth of the points close to the edge is nearer the surface of the water compared to the points away from the edge.
(b) the angle subtended by the image of the object at the eye is smaller than the actual angle subtended by the object in the air.
(c) some of the points of the object far away from the edge may not be visible because of total internal reflection.
(d) water in a trough acts as a lens and magnifies the object.
Answer: (a) the apparent depth of the points close to the edge is nearer the surface of the water compared to the points away from the edge. (b) the angle subtended by the image of the object at the...
A car is moving with at a constant speed of 60 km h–1 on a straight road. Looking at the rearview mirror, the driver finds that the car following him is at a distance of 100 m and is approaching with a speed of 5 km h –1. In order to keep track of the car in the rear, the driver begins to glance alternatively at the rear and side mirror of his car after every 2 still the other car overtakes. If the two cars were maintaining their speeds, which of the following statement (s) is/are correct?
(a) The speed of the car in the rear is 65 km h–1.
(b) In the side mirror, the car in the rear would appear to approach with a speed of 5 km h–1 to the driver of the leading car.
(c) In the rearview mirror the speed of the approaching car would appear to decrease as the distance between the cars decreases.
(d) In the side mirror, the speed of the approaching car would appear to increase as the distance between the cars decreases.
Answer: (d) In the side mirror, the speed of the approaching car would appear to increase as the distance between the cars decreases.
The optical density of turpentine is higher than that of water while its mass density is lower. The figure shows a layer of turpentine floating over water in a container. For which one of the four rays incident on turpentine in the figure, the path shown is correct?
a) 1
b) 2
c) 3
d) 4
Answer: b) 2 When light travels from (optically) rarer medium air to optically denser medium turpentine, it bends towards the normal, i.e., θ1 >...
The direction of a ray of light incident on a concave mirror as shown by PQ while directions in which the ray would travel after reflection is shown by four rays marked 1, 2, 3, and 4. Which of the four rays correctly shows the direction of reflected ray?
a) 1
b) 2
c) 3
d) 4
Answer: b) 2 After reflection, the ray PQ of light that passes through focus F and strikes the concave mirror should become parallel to the primary...
The phenomena involved in the reflection of radiowaves by ionosphere is similar to
a) reflection of light by a plane mirror
b) total internal reflection of light in the air during a mirage
c) dispersion of light by water molecules during the formation of a rainbow
d) scattering of light by the particles of air
Answer: b) total internal reflection of light in the air during a mirage The ionosphere, a layer of the atmosphere, reflects radio waves, allowing them to reach far-flung portions of the globe....
The radius of curvature of the curved surface of a plano-convex lens is 20 cm. If the refractive index of the material of the lens be 1.5, it will
a) act as a convex lens only for the objects that lie on its curved side
b) act as a concave lens only for the objects that lie on its curved side
c) act as a convex lens irrespective of the side on which the object lies
d) act as a concave lens irrespective of the side on which the object lies
Answer: c) act as a convex lens irrespective of the side on which the object lies
A passenger in an aeroplane shall
a) never see a rainbow
b) may see a primary and a secondary rainbow as concentric circles
c) may see a primary and a secondary rainbow as concentric arcs
d) shall never see a secondary rainbow
Answer: b) may see a primary and a secondary rainbow as concentric circles As an aeroplane flies higher in the sky, passengers may notice a primary and secondary rainbow in the form of concentric...
An object approaches a convergent lens from the left of the lens with a uniform speed 5 m/s and stops at the focus. The image
a) moves away from the lens with a uniform speed 5 m/s
b) moves away from the lens with a uniform acceleration
c) moves away from the lens with a non-uniform acceleration
d) moves towards the lens with a non-uniform acceleration
Answer: c) moves away from the lens with a non-uniform acceleration In our case, the object approaches a convergent lens from the left at a uniform speed of 5 m/s, causing the image to travel away...
A short pulse of white light is incident from air to a glass slab at normal incidence. After travelling through the slab, the first colour to emerge is
a) blue
b) green
c) violet
d) red
Answer: d) Red The relation v = fλ describes the velocity of a wave. The frequency of light does not change when it travels from one medium to another. As a result, the bigger the wavelength, the...
Equipotential surfaces a) are closer in regions of large electric fields compared to regions of lower electric fields b) will be more crowded near sharp edges of a conductor c) will be more crowded near regions of large charge densities d) will always be equally spaced
The correct answer is a) are closer in regions of large electric fields compared to regions of lower electric fields b) will be more crowded near sharp edges of a conductor c) will be more crowded...
Consider a uniform electric field in the z direction. The potential is a constant a) in all space b) for any x for a given z c) for any y for a given z d) on the x-y plane for a given z
The correct answer is b) for any x for a given z c) for any y for a given z d) on the x-y plane for a given z
A parallel plate capacitor is made of two dielectric blocks in series. One of the blocks has thickness d1 and dielectric constant k1 and the other has thickness d2 and dielectric constant k2 as shown in the figure. This arrangement can be thought of as a dielectric slab of thickness d = d1 + d2 and effective dielectric constant k. The k is a) k1d1 + k2d2/d1+d2 b) k1d1 + k2d2/k1 + k2 c) k1k2 (d1 + d2)/(k1d1 + k2d2) d) 2k1k2/k1 + k2
The correct answer is c) k1k2 (d1 + d2)/(k1d1 + k2d2)
Equipotential at a great distance from a collection of charges whose total sum is not zero are approximately a) spheres b) planes c) paraboloids d) ellipsoids
The correct answer is a) spheres
The electrostatic potential on the surface of a charged conducting sphere is 100V. Two statements are made in this regard: S1: At any point inside the sphere, the electric intensity is zero S2: At any point inside the sphere, the electrostatic potential is 100V Which of the following is a correct statement? a) S1 is true but S2 is false b) Both S1 and S2 are false c) S1 is true, S2 is also true, and S1 is the cause of S2 d) S1 is true, S2 is also true but the statements are independent
The correct answer is c) S1 is true, S2 is also true, and S1 is the cause of S2
Figure shows some equipotential lines distributed in space. A charged object is moved from point A to point B. a) the work done in fig (i) is the greatest b) the work done in fig (ii) is least c) the work done is the same in fig (i), fig (ii), and fig (iii) d) the work done in fig (iii) is greater than fig (ii) but equal to that in fig (i)
The correct answer is c) the work done is the same in fig (i), fig (ii), and fig (iii)
A capacitor of 4μF is connected as shown in the circuit. The internal resistance of the battery is 0.5Ω. The amount of charge on the capacitor plates will be a) 0 b) 4μC c) 16μC d) 8μC
The correct answer is d) 8μC
A ball is dropped and its displacement vs time graph is as shown in the figure where displacement x is from the ground and all quantities are positive upwards. a) Plot qualitatively velocity vs time graph b) Plot qualitatively acceleration vs time graph
a) At t=0 and v=0 , v-t graph is: b) At x = 0, a-t graph is:
A positively charged particle is released from rest in a uniform electric field. The electric potential energy of the charge a) remains a constant because the electric field is uniform b) increases because the charge moves along the electric field c) decreases because the charge moves along the electric field d) decreases because the charge moves opposite to the electric field
The correct answer is c) decreases because the charge moves along the electric field
Graph the solution sets of the following inequations: 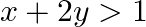
Given $x+2 y>1$ $\begin{array}{l} \Rightarrow 2 y>1-x \\ \Rightarrow y>\frac{1}{2}-\frac{x}{2} \end{array}$ Consider the equation $y=\frac{1}{2}-\frac{x}{2}$ Finding points on the...
A manufacturer produces two Models of bikes – Model 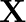 and Model
and Model 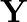 . Model
. Model 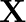 takes 6 man-hours to make per unit, while Model Y takes 10 man-hours per unit. There is a total of 450 man-hour available per week. Handling and Marketing costs are Rs 2000 and Rs 1000 per unit for Models
takes 6 man-hours to make per unit, while Model Y takes 10 man-hours per unit. There is a total of 450 man-hour available per week. Handling and Marketing costs are Rs 2000 and Rs 1000 per unit for Models 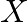 and
and 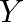 respectively. The total funds available for these purposes are Rs 80,000 per week. Profits per unit for Models
respectively. The total funds available for these purposes are Rs 80,000 per week. Profits per unit for Models 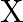 and
and 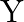 are Rs 1000 and Rs 500 , respectively. How many bikes of each model should the manufacturer produce so as to yield a maximum profit? Find the maximum profit.
are Rs 1000 and Rs 500 , respectively. How many bikes of each model should the manufacturer produce so as to yield a maximum profit? Find the maximum profit.
Solution: Let us take $\mathrm{x}$ an $\mathrm{y}$ to be the no. of models of bike produced by the manufacturer. From the question we have, Model $x$ takes 6 man-hours to make per unit Model $y$...
In Fig. 12.11, the feasible region (shaded) for a LPP is shown. Determine the maximum and minimum value of 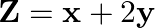
Solution: It is seen from the given figure, that the corner points are as follows: $\mathrm{R}(7 / 2,3 / 4), \mathrm{Q}(3 / 2,15 / 4), \mathrm{P}(3 / 13,24 / 13)$ and $\mathrm{S}(18 / 7,2 / 7)$ On...
Minimize 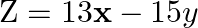 subject to the constraints:
subject to the constraints: 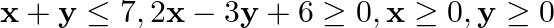 .
.
Solution: It is given that: $\mathrm{Z}=13 \mathrm{x}-15 \mathrm{y}$ and the constraints $\mathrm{x}+\mathrm{y} \leq 7$, $2 x-3 y+6 \geq 0, x \geq 0, y \geq 0$ Taking $x+y=7$, we have...
Maximize 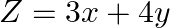 , subject to the constraints:
, subject to the constraints: 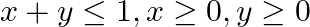
Solution: It is given that: $Z=3 x+4 y$ and the constraints $x+y \leq 1, x \geq 0$ $\mathrm{y} \geq 0$ Taking $x+y=1$, we have $$\begin{tabular}{|l|l|l|} \hline$x$ & 1 & 0 \\ \hline$y$ & 0 & 1 \\...
Determine the maximum value of 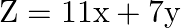 subject to the constraints:
subject to the constraints: 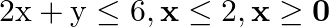
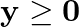
Solution: It is given that: $\mathrm{Z}=11 \mathrm{x}+7 \mathrm{y}$ and the constraints $2 \mathrm{x}+\mathrm{y} \leq 6, \mathrm{x} \leq 2, \mathrm{x} \geq 0, \mathrm{y} \geq 0$ Let $2 x+y=6$...
Find the values of p so that the lines 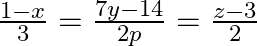 and
and 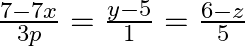 are at right angles.
are at right angles.
Solution: The standard form of a pair of Cartesian lines is:...
A die is tossed twice. A ‘success’ is getting an even number on a toss. Find the variance of the number of successes.
Let’s consider E to be the event of getting even number on tossing a die.
Two cards are drawn successively without replacement from a well shuffled deck of cards. Find the mean and standard variation of the random variable X where X is the number of aces.
Let’s consider X to be the random variable such that X = \[0,1,2\] Now, let E = the event of drawing an ace And, F = the event of drawing non – ace So,
A bag contains ![Rendered by QuickLaTeX.com \[(2n+1)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-78b5bf57e27382de024d05e8d0d3a07f_l3.png)
coins. It is known that n of these coins has a head on both sides whereas the rest of the coins are fair. A coin is picked up at random from the bag and is tossed. If the probability that the toss results in a head is ![Rendered by QuickLaTeX.com \[31/42\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-849c6b533cd29d9a5cbe8eee0858947f_l3.png)
, determine the value of n.
Given, n coins are two headed coins and the remaining \[(n+1)\] coins are fair. Let \[{{E}_{1}}\] : the event that unfair coin is selected \[{{E}_{2}}\] : the event that the fair coin is selected...
The probability distribution of a random variable x is given as under: where k is a constant. Calculate (i) E(X) (ii) ![Rendered by QuickLaTeX.com \[\mathbf{E}\text{ }(\mathbf{3}{{\mathbf{X}}^{\mathbf{2}}})\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-359841d615186c48f07fb2ecf9ffc135_l3.png)
(iii) ![Rendered by QuickLaTeX.com \[\mathbf{P}\left( \mathbf{X}\text{ }{}^\text{3}\text{ }\mathbf{4} \right)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-bef0b1e97b70143ca1a104413a9288cb_l3.png)
The probability distribution of random variable X is given by: We know that \[\sum\limits_{i=1}^{n}{P({{X}_{i}})=1}\] So, \[k\text{ }+\text{ }4k\text{ }+\text{ }9k\text{ }+\text{ }8k\text{ }+\text{...
The probability distribution of a discrete random variable X is given as under: Calculate: (i) The value of A if E(X) = ![Rendered by QuickLaTeX.com \[2.94\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-dc4a155e0dbba391251d3c9a51f46671_l3.png)
(ii) Variance of X.
(i) We know that: (ii) Now, the distribution becomes \[E({{X}^{2}})\text{ }=\text{ }1\text{ }\times \text{ 1/2 }+\text{ }4\text{ }\times \text{ }1/5\text{ }+\text{ }16\text{ }\times 3/25\text{...
Let X be a discrete random variable whose probability distribution is defined as follows: where k is a constant. Calculate (i) the value of k (ii) E (X) (iii) Standard deviation of X.
(i) Given, \[P\left( X\text{ }=\text{ }x \right)\text{ }=\text{ }k\left( x\text{ }+\text{ }1 \right)\]for \[x\text{ }=\text{ }1,\text{ }2,\text{ }3,\text{ }4\] So, \[P\left( X\text{ }=\text{ }1...
An item is manufactured by three machines A, B and C. Out of the total number of items manufactured during a specified period, ![Rendered by QuickLaTeX.com \[50%\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-ca149718e5307dc632f1a645fa126949_l3.png)
are manufactured on A, ![Rendered by QuickLaTeX.com \[30%\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-0b64632b3753893445e430101db07114_l3.png)
on B and ![Rendered by QuickLaTeX.com \[20%\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1ed6297f4c9a6cc3a7308d2bf71d5c46_l3.png)
on C. ![Rendered by QuickLaTeX.com \[2%\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f829dab9c621cc182071a81cb5fc9019_l3.png)
of the items produced on A and ![Rendered by QuickLaTeX.com \[2%\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f829dab9c621cc182071a81cb5fc9019_l3.png)
of items produced on B are defective, and ![Rendered by QuickLaTeX.com \[3%\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-abb61d3b72337a4d446ae396fc41e29f_l3.png)
of these produced on C are defective. All the items are stored at one godown. One item is drawn at random and is found to be defective. What is the probability that it was manufactured on machine A?
Let’s consider: \[{{E}_{1}}\] = The event that the item is manufactured on machine A \[{{E}_{2}}\] = The event that the item is manufactured on machine B \[{{E}_{3}}\] = The event that the item is...
By examining the chest X ray, the probability that TB is detected when a person is actually suffering is ![Rendered by QuickLaTeX.com \[0.99\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-fd481c2d31920faa29c05d71c567faeb_l3.png)
. The probability of an healthy person diagnosed to have TB is ![Rendered by QuickLaTeX.com \[0.001\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-8760ed286b6e77e1e8cc18398e05425c_l3.png)
. In a certain city, ![Rendered by QuickLaTeX.com \[1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-64318110f3a374fb786ef713c0b0c575_l3.png)
in ![Rendered by QuickLaTeX.com \[1000\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-19afebc5b07af7e6daa7a65dc0d832c8_l3.png)
people suffers from TB. A person is selected at random and is diagnosed to have TB. What is the probability that he actually has TB?
Let \[{{E}_{1}}\] = Event that a person has TB \[{{E}_{2}}\] = Event that a person does not have TB And H = Event that the person is diagnosed to have TB. So, \[P({{E}_{1}})\text{ }=\text{...
There are three urns containing ![Rendered by QuickLaTeX.com \[2\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b1e8e3db630df9050b1fec3c4066d5e6_l3.png)
white and ![Rendered by QuickLaTeX.com \[3\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-df8bcc09db12acd0f6bda88b4b8135fb_l3.png)
black balls, ![Rendered by QuickLaTeX.com \[3\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-df8bcc09db12acd0f6bda88b4b8135fb_l3.png)
white and ![Rendered by QuickLaTeX.com \[2\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b1e8e3db630df9050b1fec3c4066d5e6_l3.png)
black balls, and ![Rendered by QuickLaTeX.com \[4\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3c0fa656ae249b0b1e03c8cd2e7be583_l3.png)
white and ![Rendered by QuickLaTeX.com \[1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-64318110f3a374fb786ef713c0b0c575_l3.png)
black balls, respectively. There is an equal probability of each urn being chosen. A ball is drawn at random from the chosen urn and it is found to be white. Find the probability that the ball drawn was from the second urn.
Given, we have \[3\] urns: Urn \[1\] = \[2\] white and \[3\] black balls Urn \[2\] = \[3\] white and 2 black balls Urn \[3\] = \[4\] white and \[1\] black balls Now, the probabilities of choosing...
There are two bags, one of which contains ![Rendered by QuickLaTeX.com \[3\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-df8bcc09db12acd0f6bda88b4b8135fb_l3.png)
black and ![Rendered by QuickLaTeX.com \[4\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3c0fa656ae249b0b1e03c8cd2e7be583_l3.png)
white balls while the other contains ![Rendered by QuickLaTeX.com \[4\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3c0fa656ae249b0b1e03c8cd2e7be583_l3.png)
black and ![Rendered by QuickLaTeX.com \[3\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-df8bcc09db12acd0f6bda88b4b8135fb_l3.png)
white balls. A die is thrown. If it shows up ![Rendered by QuickLaTeX.com \[1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-64318110f3a374fb786ef713c0b0c575_l3.png)
or ![Rendered by QuickLaTeX.com \[3\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-df8bcc09db12acd0f6bda88b4b8135fb_l3.png)
, a ball is taken from the Ist bag; but it shows up any other number, a ball is chosen from the second bag. Find the probability of choosing a black ball.
Let \[{{E}_{1}}\] be the event of selecting Bag \[1\] and \[{{E}_{2}}\] be the event of selecting Bag \[2\]. Also, let \[{{E}_{3}}\] be the event that black ball is selected Now,...
A letter is known to have come either from TATA NAGAR or from CALCUTTA. On the envelope, just two consecutive letter TA are visible. What is the probability that the letter came from TATA NAGAR.
Let E1 be the event that the letter comes from TATA NAGAR, E2 be the event that the letter comes from CALCUTTA And, E3 be the event that on the letter, two consecutive letters TA are visible Now,...
A shopkeeper sells three types of flower seeds ![Rendered by QuickLaTeX.com \[{{A}_{1}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-341e1e984315ed13927449714dabfaa2_l3.png)
, ![Rendered by QuickLaTeX.com \[{{A}_{2}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d968864b145166cde507df94fe7956a5_l3.png)
and ![Rendered by QuickLaTeX.com \[{{A}_{3}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-6b8e7ede3efe150d0c00b572c6914dd9_l3.png)
. They are sold as a mixture where the proportions are ![Rendered by QuickLaTeX.com \[4:4:2\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d053586997c365d9619155a2d9fe786f_l3.png)
respectively. The germination rates of the three types of seeds are ![Rendered by QuickLaTeX.com \[45%\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-4672977ce8f8e9c25d696506eb42964f_l3.png)
, ![Rendered by QuickLaTeX.com \[60%\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-11d0f318e7df09d336d4dab5cfbaab92_l3.png)
and ![Rendered by QuickLaTeX.com \[35%\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b6c3c41c5dc923325bad3c432273efeb_l3.png)
. Calculate the probability (i) of a randomly chosen seed to germinate (ii) that it will not germinate given that the seed is of type A3, (iii) that it is of the type A2 given that a randomly chosen seed does not germinate.
Given that: \[{{A}_{1}}:\text{ }{{A}_{2}}:\text{ }{{A}_{3}}~=\text{ }4:\text{ }4:\text{ }2\] So, the probabilities will be \[P({{A}_{1}})\text{ }=\text{ }4/10,\text{ }P({{A}_{2}})\text{ }=\text{...
Refer to Question 41 above. If a white ball is selected, what is the probability that it came from (i) Bag ![Rendered by QuickLaTeX.com \[2\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b1e8e3db630df9050b1fec3c4066d5e6_l3.png)
(ii) Bag ![Rendered by QuickLaTeX.com \[3\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-df8bcc09db12acd0f6bda88b4b8135fb_l3.png)
Referring the Question 41, here we will use Baye’s Theorem Therefore, the required probabilities are \[2/11\] and \[9/11\].
Three bags contain a number of red and white balls as follows: Bag ![Rendered by QuickLaTeX.com \[1:3\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-ba8b0b5a4435fb6e4683c37d89e7a21a_l3.png)
red balls, Bag ![Rendered by QuickLaTeX.com \[2:2\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a7d38a7155c877210158a7e2ae0d07a6_l3.png)
red balls and ![Rendered by QuickLaTeX.com \[1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-64318110f3a374fb786ef713c0b0c575_l3.png)
white ball Bag ![Rendered by QuickLaTeX.com \[3:3\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-6ac2477a33ed3fd2d9a24a48cdfcc4f6_l3.png)
white balls. The probability that bag i will be chosen and a ball is selected from it is ![Rendered by QuickLaTeX.com \[\mathbf{i}/\mathbf{6},\text{ }\mathbf{i}\text{ }=\text{ }\mathbf{1},\text{ }\mathbf{2},\text{ }\mathbf{3}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3879abc07693612c912b0b2e40f714ab_l3.png)
. What is the probability that (i) a red ball will be selected? (ii) a white ball is selected?
Given: Bag \[1:3\] red balls, Bag \[2:2\] red balls and \[1\] white ball Bag \[3:3\] white balls Now, let E1, E2 and E3 be the events of choosing Bag \[1\], Bag \[2\] and Bag \[3\] respectively and...
Find the vector and the Cartesian equations of the line that passes through the points (3, –2, –5), (3, –2, 6).
Solution: It is given that Let's calculate the vector form: The vector eq. of as line which passes through two points whose position vectors are $\vec{a}$ and $\vec{b}$ is...
An urn contains m white and n black balls. A ball is drawn at random and is put back into the urn along with k additional balls of the same colour as that of the ball drawn. A ball is again drawn at random. Show that the probability of drawing a white ball now does not depend on k.
Let’s consider A to be the event of having m white and n black balls \[{{E}_{1}}\] = First ball drawn of white colour \[{{E}_{2}}\] = First ball drawn of black colour \[{{E}_{3}}\] = Second ball...
Two dice are tossed. Find whether the following two events A and B are independent: ![Rendered by QuickLaTeX.com \[\mathbf{A}\text{ }=\text{ }\left\{ \left( x,~y \right)\text{ }:~x~+~y~=\text{ }\mathbf{11} \right\}\text{ }\mathbf{B}\text{ }=\text{ }\left\{ \left( x,~y \right)\text{ }:~x~{}^\text{1}\text{ }\mathbf{5} \right\}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-885675871c9e120053f074fc2dfbccab_l3.png)
where (x, y) denotes a typical sample point.
Given, two events A and B are independent such that \[\mathbf{A}\text{ }=\text{ }\left\{ \left( x,~y \right)\text{ }:~x~+~y~=\text{ }\mathbf{11} \right\}\text{ }\mathbf{B}\text{ }=\text{ }\left\{...
A and B throw a pair of dice alternately. A wins the game if he gets a total of ![Rendered by QuickLaTeX.com \[6\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-dba464f544e5646eaa291e02993dca75_l3.png)
and B wins if she gets a total of ![Rendered by QuickLaTeX.com \[7\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-6064bfa4cc3ec5261b106372b5e270dd_l3.png)
. It A starts the game, find the probability of winning the game by A in third throw of the pair of dice.
Solution: Let’s take A1 to be the event of getting a total of \[6\] \[{{A}_{1}}~=\text{ }\left\{ \left( 2,\text{ }4 \right),\text{ }\left( 4,\text{ }2 \right),\text{ }\left( 1,\text{ }5...
Find the variance of the distribution:
We know that, Variance(X) = \[E({{X}^{2}})\text{ }\text{ }{{\left[ E\left( X \right) \right]}^{2}}\] Therefore, the required variance is \[665/324\].
The random variable X can take only the values ![Rendered by QuickLaTeX.com \[0,1,2\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f06eacfda1895c1be8bba5ac9f32610f_l3.png)
. Given that ![Rendered by QuickLaTeX.com \[\mathbf{P}\left( \mathbf{X}\text{ }=\text{ }\mathbf{0} \right)\text{ }=\text{ }\mathbf{P}\text{ }\left( \mathbf{X}\text{ }=\text{ }\mathbf{1} \right)\text{ }=~p~\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-75b90be1f325daf60ead8d2bd34b18b7_l3.png)
and that ![Rendered by QuickLaTeX.com \[\mathbf{E}({{\mathbf{X}}^{\mathbf{2}}})\text{ }=\text{ }\mathbf{E}\left[ \mathbf{X} \right]\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f884261ac4c1cb9018e81987c5d6e5e7_l3.png)
,find the value of p.
Given, \[X\text{ }=\text{ }0,\text{ }1,\text{ }2\]and \[P\left( X\text{ }=\text{ }0 \right)\text{ }=\text{ }P\text{ }\left( X\text{ }=\text{ }1 \right)\text{ }=~p\] Let P(X) at \[X\text{ }=\text{...
Find the probability distribution of the maximum of the two scores obtained when a die is thrown twice. Determine also the mean of the distribution.
Let X be the random variable scores when a die is thrown twice. \[X\text{ }=\text{ }1,\text{ }2,\text{ }3,\text{ }4,\text{ }5,\text{ }6\] And \[S\text{ }=\text{ }\left\{ \left( 1,\text{ }1...
Two natural numbers r, s are drawn one at a time, without replacement from the set ![Rendered by QuickLaTeX.com \[\mathbf{S}=\left\{ \mathbf{1},\text{ }\mathbf{2},\text{ }\mathbf{3},\text{ }\ldots .,~n \right\}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-ce22786f04ec38181dfef3cbeaeaaccb_l3.png)
. Find ![Rendered by QuickLaTeX.com \[\mathbf{P}\left[ r~\text{£}~p|s~\text{£}~p \right]\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-5dd30e9e2968f763f8ba34dc8876eb03_l3.png)
, where ![Rendered by QuickLaTeX.com \[p\mathbf{\hat{I}}S\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7430e7cd969e1b9bf6720f847694f60e_l3.png)
.
Given, \[\mathbf{S}=\left\{ \mathbf{1},\text{ }\mathbf{2},\text{ }\mathbf{3},\text{ }\ldots .,~n \right\}\] So, \[P\left( r\text{ }\le \text{ }p/s\text{ }\le \text{ }p \right)\text{ }=\text{...
Suppose that ![Rendered by QuickLaTeX.com \[6%\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-5c29929de273fef75310a23bf4feb60d_l3.png)
of the people with blood group O are left-handed and ![Rendered by QuickLaTeX.com \[10%\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1b656bc509cbbf036ef348182e0ea394_l3.png)
of those with other blood groups are left-handed ![Rendered by QuickLaTeX.com \[30%\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-0b64632b3753893445e430101db07114_l3.png)
of the people have blood group O. If a left-handed person is selected at random, what is the probability that he/she will have blood group O?
Let’s assume \[{{E}_{1}}\] = The event that a person selected is of blood group O \[{{E}_{2}}\] = The event that the people selected is of other group And H = The event that selected person is left...
Suppose you have two coins which appear identical in your pocket. You know that one is fair and one is ![Rendered by QuickLaTeX.com \[2\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b1e8e3db630df9050b1fec3c4066d5e6_l3.png)
-headed. If you take one out, toss it and get a head, what is the probability that it was a fair coin?
Let’s consider \[{{E}_{1}}\] = Event that the coin is fair \[{{E}_{2}}\] = Event that the coin is \[2\] headed And H = Event that the tossed coin gets head. Now, \[P({{E}_{1}})\text{ }=\text{...
A factory produces bulbs. The probability that any one bulb is defective is ![Rendered by QuickLaTeX.com \[1/50\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-ef97cec9629bf8a7126fa4b44586a2f6_l3.png)
and they are packed in boxes of ![Rendered by QuickLaTeX.com \[10\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7e13914576c8f07fa7780b4b1aae684d_l3.png)
. From a single box, find the probability that (i) none of the bulbs is defective (ii) exactly two bulbs are defective (iii) more than ![Rendered by QuickLaTeX.com \[8\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-5ba6e07885b354f6c76c81fbd23c392a_l3.png)
bulbs work properly
Let’s assume X to be the random variable denoting a bulb to be defective. Here, \[n\text{ }=\text{ }10,\text{ }p\text{ }=\text{ }1/50,\text{ }q\text{ }=\text{ }1\text{ }\text{ }1/50\text{ }=\text{...
Two probability distributions of the discrete random variable X and Y are given below. Prove that ![Rendered by QuickLaTeX.com \[\mathbf{E}({{\mathbf{Y}}^{\mathbf{2}}})\text{ }=\text{ }\mathbf{2}\text{ }\mathbf{E}\left( \mathbf{X} \right)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-4a5a28d43937af922c00cd90c0779f08_l3.png)
.
The probability distribution of random variable X is We know that, \[E(X)=\sum\limits_{i=1}^{n}{{{P}_{i}}{{X}_{i}}}\] \[E\left( X \right)\text{ }0.\text{ }1/5\text{ }+\text{ }1.\text{ }2/5\text{...
Two biased dice are thrown together. For the first die ![Rendered by QuickLaTeX.com \[\mathbf{P}\left( \mathbf{6} \right)\text{ }=\text{ }\mathbf{1}/\mathbf{2}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d706b45772502fefb7902470436e85d1_l3.png)
, the other scores being equally likely while for the second die, ![Rendered by QuickLaTeX.com \[\mathbf{P}\left( \mathbf{1} \right)\text{ }=\text{ }\mathbf{2}/\mathbf{5}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1d0bc14040ccf34dc77d24157b844fae_l3.png)
and the other scores are equally likely. Find the probability distribution of ‘the number of ones seen’.
Therefore, the required probability distribution is
A die is thrown three times. Let X be ‘the number of twos seen’. Find the expectation of X.
Here, we have \[X\text{ }=\text{ }0,\text{ }1,\text{ }2,\text{ }3\] [Since, die is thrown \[3\] times] And \[p\text{ }=\text{ }1/6,\text{ }q\text{ }=\text{ }5/6\] Therefore, the required expression...
A biased die is such that ![Rendered by QuickLaTeX.com \[\mathbf{P}\left( \mathbf{4} \right)\text{ }=\text{ }\mathbf{1}/\mathbf{10}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c61e00ee1511c576a624b03eb5365058_l3.png)
and other scores being equally likely. The die is tossed twice. If X is the ‘number of fours seen’, find the variance of the random variable X.
Here, random variable \[X\text{ }=\text{ }0,\text{ }1,\text{ }2\] \[P\left( X\text{ }=\text{ }2 \right)\text{ }=\text{ }P\left( 4 \right).P\left( 4 \right)\text{ }=\text{ }1/10\text{ }x\text{...
For the following probability distribution determine standard deviation of the random variable X.
We know that: Standard deviation (S.D.) = \[\sqrt{Variance}\] So, \[Var\left( X \right)\text{ }=\text{ }E({{X}^{2}})\text{ }\text{ }{{\left[ E\left( X \right) \right]}^{2}}\] \[E\left( X...
The probability distribution of a random variable X is given below: (i) Determine the value of k. (ii) Determine ![Rendered by QuickLaTeX.com \[\mathbf{P}\left( \mathbf{X}\text{ }\text{£}\text{ }\mathbf{2} \right)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7219c5472010a2f5c3011ed7e15c0d3a_l3.png)
and ![Rendered by QuickLaTeX.com \[\mathbf{P}\left( \mathbf{X}\text{ }>\text{ }\mathbf{2} \right)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d954dc3284a88e08e4854fc070c65966_l3.png)
(iii) Find ![Rendered by QuickLaTeX.com \[\mathbf{P}\left( \mathbf{X}\text{ }\text{£}\text{ }\mathbf{2} \right)\text{ }+\text{ }\mathbf{P}\text{ }\left( \mathbf{X}\text{ }>\text{ }\mathbf{2} \right)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b2408d7c2c095809b69385b1a8434f7f_l3.png)
(i) W.k.t \[P\left( 0 \right)\text{ }+\text{ }P\left( 1 \right)\text{ }+\text{ }P\left( 2 \right)\text{ }+\text{ }P\left( 3 \right)\text{ }=\text{ }1\] \[\Rightarrow k\text{ }+\text{ }k/2\text{...
Consider the probability distribution of a random variable X: Calculate: (i) ![Rendered by QuickLaTeX.com \[\mathbf{V}\left( \mathbf{X}/\mathbf{2} \right)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-e9101e3d5c183bb25d79a8270ac6dfab_l3.png)
(ii) Variance of X.
Given We know that: \[\mathbf{Var}\left( \mathbf{X} \right)\text{ }=\text{ }\mathbf{E}({{\mathbf{X}}^{\mathbf{2}}})\text{ }\text{ }{{\left[ \mathbf{E}\left( \mathbf{X} \right)...
A lot of ![Rendered by QuickLaTeX.com \[100\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a40261fc9a48539be6f3f3cac1241623_l3.png)
watches is known to have ![Rendered by QuickLaTeX.com \[10\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7e13914576c8f07fa7780b4b1aae684d_l3.png)
defective watches. If 8 watches are selected (one by one with replacement) at random, what is the probability that there will be at least one defective watch?
Given: Total number of watches = \[100\] and number of defective watches = \[10\] So, the probability of selecting a detective watch = \[10/100\text{ }=\text{ }1/10\] Now, n = \[8\], \[p\text{...
The probability of a man hitting a target is ![Rendered by QuickLaTeX.com \[0.25\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-906d3b7cfc769cdde9f6b42bddf212a4_l3.png)
. He shoots ![Rendered by QuickLaTeX.com \[7\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-6064bfa4cc3ec5261b106372b5e270dd_l3.png)
times. What is the probability of his hitting at least twice?
Here, we have n = \[7\], \[p\text{ }=\text{ }0.25\text{ }=\text{ }25/100\text{ }=\text{ 1/4}\] and \[q=1-1/4=3/4\] \[P\left( X\text{ }\ge \text{ }2 \right)\text{ }=\text{ }1\text{ }\text{ }\left[...
Ten coins are tossed. What is the probability of getting at least 8 heads?
Here we have, \[n=10\], \[p=1/2\] and \[q=1-1/2=1/2\] \[P\left( X\text{ }\ge \text{ }8 \right)\text{ }=\text{ }P\left( x\text{ }=\text{ }8 \right)\text{ }+\text{ }P\left( x\text{ }=\text{ }9...
A die is thrown ![Rendered by QuickLaTeX.com \[5\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7dc8465919d0838925dbc6c99670258c_l3.png)
times. Find the probability that an odd number will come up exactly three times.
Here, \[p\text{ }=\text{ }1/6\text{ }+\text{ }1/6\text{ }+\text{ }1/6\text{ }=\text{ 1/2}\Rightarrow q\text{ }=\text{ }1\text{ }\text{ 1/2 }=\text{ 1/2}\] and \[n=5\] Now, \[P\left( x\text{ }=\text{...
Four cards are successively drawn without replacement from a deck of ![Rendered by QuickLaTeX.com \[52\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-86d14a8f8f75bf6cce4aee265685d74c_l3.png)
playing cards. What is the probability that all the four cards are kings?
Let \[{{E}_{1}},{{E}_{2}},{{E}_{3}}\] and \[{{E}_{4}}\] be the events that first, second, third and fourth card is King respectively. Therefore, the required probability is \[1/27075\].
A box has ![Rendered by QuickLaTeX.com \[5\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7dc8465919d0838925dbc6c99670258c_l3.png)
blue and ![Rendered by QuickLaTeX.com \[4\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3c0fa656ae249b0b1e03c8cd2e7be583_l3.png)
red balls. One ball is drawn at random and not replaced. Its colour is also not noted. Then another ball is drawn at random. What is the probability of second ball being blue?
Given that the box has \[5\] blue and \[4\] red balls. Let us consider \[{{E}_{1}}\] be the event that first ball drawn is blue and \[{{E}_{2}}\] be the event that first ball drawn is red. And, E is...
Bag I contains ![Rendered by QuickLaTeX.com \[3\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-df8bcc09db12acd0f6bda88b4b8135fb_l3.png)
black and ![Rendered by QuickLaTeX.com \[2\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b1e8e3db630df9050b1fec3c4066d5e6_l3.png)
white balls, Bag II contains ![Rendered by QuickLaTeX.com \[2\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b1e8e3db630df9050b1fec3c4066d5e6_l3.png)
black and ![Rendered by QuickLaTeX.com \[4\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3c0fa656ae249b0b1e03c8cd2e7be583_l3.png)
white balls. A bag and a ball is selected at random. Determine the probability of selecting a black ball.
According to the question: Bag \[1\] has \[3\]B, \[2\]W balls and Bag \[2\] has \[2\]B, \[4\]W balls. Let \[{{E}_{1}}\] = The event that bag \[1\] is selected \[{{E}_{2}}\] = The event that bag...
A bag contains ![Rendered by QuickLaTeX.com \[4\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3c0fa656ae249b0b1e03c8cd2e7be583_l3.png)
white and ![Rendered by QuickLaTeX.com \[5\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7dc8465919d0838925dbc6c99670258c_l3.png)
black balls. Another bag contains ![Rendered by QuickLaTeX.com \[9\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-eda27e23820084685a09a6f91d2210f2_l3.png)
white and ![Rendered by QuickLaTeX.com \[7\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-6064bfa4cc3ec5261b106372b5e270dd_l3.png)
black balls. A ball is transferred from the first bag to the second and then a ball is drawn at random from the second bag. Find the probability that the ball drawn is white.
Let us consider \[{{W}_{1}}\] and \[{{W}_{2}}\] to be two bags containing \[\left( 4W,\text{ }5B \right)\]and \[\left( 9W,\text{ }7B \right)\]balls respectively. Let us take \[{{E}_{1}}\] be the...
Suppose ![Rendered by QuickLaTeX.com \[10,000\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d779de9f724f9dd4498a634de29e75ee_l3.png)
tickets are sold in a lottery each for Re ![Rendered by QuickLaTeX.com \[1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-64318110f3a374fb786ef713c0b0c575_l3.png)
. First prize is of Rs ![Rendered by QuickLaTeX.com \[3000\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-38a530e94753e67a9a2398736eb825ed_l3.png)
and the second prize is of Rs. ![Rendered by QuickLaTeX.com \[2000\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f1d2240de6dcb447376df455f7650d37_l3.png)
. There are three third prizes of Rs. ![Rendered by QuickLaTeX.com \[500\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-6ab5d1c783918e412f33f2a0d6a52a71_l3.png)
each. If you buy one ticket, what is your expectation.
Let’s take X to be the random variable where X = \[0,500,2000\]and \[3000\]
Three dice are thrown at the same time. Find the probability of getting three two’s, if it is known that the sum of the numbers on the dice was six.
Given that the dice is thrown three times So, the sample space n(S) = \[{{6}^{3}}~=\text{ }216\] Let E1 be the event when the sum of number on the dice was \[6\] and \[{{E}_{2}}\]be the event when...
In a dice game, a player pays a stake of Re ![Rendered by QuickLaTeX.com \[1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-64318110f3a374fb786ef713c0b0c575_l3.png)
for each throw of a die. She receives Rs ![Rendered by QuickLaTeX.com \[5\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7dc8465919d0838925dbc6c99670258c_l3.png)
if the die shows a ![Rendered by QuickLaTeX.com \[3\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-df8bcc09db12acd0f6bda88b4b8135fb_l3.png)
, Rs ![Rendered by QuickLaTeX.com \[2\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b1e8e3db630df9050b1fec3c4066d5e6_l3.png)
if the die shows a ![Rendered by QuickLaTeX.com \[1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-64318110f3a374fb786ef713c0b0c575_l3.png)
or ![Rendered by QuickLaTeX.com \[6\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-dba464f544e5646eaa291e02993dca75_l3.png)
, and nothing otherwise. What is the player’s expected profit per throw over a long series of throws?
Let’s take X to be the random variable of profit per throw. As, she loses Rs \[1\] for giving any od \[2,4,5\]. So, \[P\left( X\text{ }=\text{ }-1 \right)\text{ }=\text{ }1/6\text{ }+\text{...
If X is the number of tails in three tosses of a coin, determine the standard deviation of X.
Given, \[X\text{ }=\text{ }0,\text{ }1,\text{ }2,\text{ }3\] P(X = r) \[={{~}^{n}}{{C}_{r}}~{{p}^{r}}~{{q}^{n-r}}\] Where \[n\text{ }=\text{ }3,\text{ }p\text{ }=\text{ 1/2},\text{ }q\text{ }=\text{...
Prove that (i) P(A) = ![Rendered by QuickLaTeX.com \[\mathbf{P}\left( \mathbf{A}\text{ }\mathbf{B} \right)\text{ }+\text{ }\mathbf{P}\left( \mathbf{A}~B~ \right)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-891f8144a3d214e2468e25bfa6c9744a_l3.png)
(ii) ![Rendered by QuickLaTeX.com \[\mathbf{P}\left( \mathbf{A\grave{E}}\text{ }\mathbf{B} \right)\text{ }=\text{ }\mathbf{P}\left( \mathbf{A}\text{ }\mathbf{B} \right)\text{ }+\text{ }\mathbf{P}\left( \mathbf{A}~B~ \right)\text{ }+\text{ }\mathbf{P}\left( ~A~\mathbf{}\text{ }\mathbf{B} \right)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-503b374a6572f014a7922e0698acabb6_l3.png)
![Rendered by QuickLaTeX.com \[\mathbf{P}\left( \mathbf{A\grave{E}}\text{ }\mathbf{B} \right)\text{ }=\text{ }\mathbf{P}\left( \mathbf{A}\text{ }\mathbf{B} \right)\text{ }+\text{ }\mathbf{P}\left( \mathbf{A}~B~ \right)\text{ }+\text{ }\mathbf{P}\left( ~A~\mathbf{}\text{ }\mathbf{B} \right)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-503b374a6572f014a7922e0698acabb6_l3.png)
A discrete random variable X has the probability distribution given as below: (i) Find the value of k (ii) Determine the mean of the distribution.
For a probability distribution, we know that if \[{{P}_{i}}~\ge \text{ }0\]
Let E1 and E2 be two independent events such that ![Rendered by QuickLaTeX.com \[p({{\mathbf{E}}_{\mathbf{1}}})\text{ }=~{{p}_{\mathbf{1}}}~\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d36a1b249458751ac0b7265c3f2feae0_l3.png)
and ![Rendered by QuickLaTeX.com \[\mathbf{P}({{\mathbf{E}}_{\mathbf{2}}})\text{ }=\text{ }{{\mathbf{p}}_{\mathbf{2}}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-9e51eb6f05253a43a1f8b33827d4a78c_l3.png)
. Describe in words of the events whose probabilities are: ![Rendered by QuickLaTeX.com \[\left( \mathbf{i} \right)~{{p}_{\mathbf{1}}}~{{p}_{\mathbf{2}}}~\left( \mathbf{ii} \right)\text{ }(\mathbf{1}{{p}_{\mathbf{1}}})~{{p}_{\mathbf{2}}}~\left( \mathbf{iii} \right)\text{ }\mathbf{1}\text{ }\text{ }(\mathbf{1}\text{ }~{{p}_{\mathbf{1}}})(\mathbf{1}\text{ }~{{p}_{\mathbf{2}}})\text{ }\left( \mathbf{iv} \right)~{{p}_{\mathbf{1}}}~+~{{p}_{\mathbf{2}}}~\text{ }\mathbf{2}{{p}_{\mathbf{1}}}{{p}_{\mathbf{2}}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-9ab664e4b24993ddb3c0cb24b5193ff7_l3.png)
Here, \[p({{\mathbf{E}}_{\mathbf{1}}})\text{ }=~{{p}_{\mathbf{1}}}~\] and \[\mathbf{P}({{\mathbf{E}}_{\mathbf{2}}})\text{ }=\text{ }{{\mathbf{p}}_{\mathbf{2}}}\] Now, its clearly seen that either...
Three events A, B and C have probabilities ![Rendered by QuickLaTeX.com \[2/5\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-65f2bd55c9cd4b5a8e52a02c046795a8_l3.png)
, ![Rendered by QuickLaTeX.com \[1/3\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-594dbc2654244fc13c5110dcc1f09b05_l3.png)
and ![Rendered by QuickLaTeX.com \[1/2\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-dec193819dbd46464760da9f9d8f2f08_l3.png)
respectively. Given that ![Rendered by QuickLaTeX.com \[\mathbf{P}\left( \mathbf{A}\text{ }\mathbf{C} \right)\text{ }=\text{ }\mathbf{1}/\mathbf{5}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b881a1a9b199441313766b0526805d42_l3.png)
and ![Rendered by QuickLaTeX.com \[\mathbf{P}\left( \mathbf{B}\text{ }\mathbf{}\text{ }\mathbf{C} \right)\text{ }=\text{ 1/4}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b3887f38cc88ac2b2b0c43663de29501_l3.png)
, find the values of ![Rendered by QuickLaTeX.com \[\mathbf{P}\left( \mathbf{C}\text{ }|\text{ }\mathbf{B} \right)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3d783de9e6bdfea383b4c74d246a12e3_l3.png)
and ![Rendered by QuickLaTeX.com \[\mathbf{P}\left( \mathbf{A}\mathbf{}\text{ }\mathbf{C} \right)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-67318d5897bac72c39ae64c15de35bf0_l3.png)
.
Given, P(A) = \[2/5\], P(B) = \[1/3\] and P(C) = \[1/2\] \[\mathbf{P}\left( \mathbf{A}\text{ }\mathbf{C} \right)\text{ }=\text{ }\mathbf{1}/\mathbf{5}\]and \[\mathbf{P}\left( \mathbf{B}\text{...
A and B are two events such that P(A) = ![Rendered by QuickLaTeX.com \[1/2\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-dec193819dbd46464760da9f9d8f2f08_l3.png)
, P(B) = ![Rendered by QuickLaTeX.com \[1/3\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-594dbc2654244fc13c5110dcc1f09b05_l3.png)
and ![Rendered by QuickLaTeX.com \[\mathbf{P}\left( \mathbf{A}\text{ }\mathbf{}\text{ }\mathbf{B} \right)\text{ }=\text{ }\mathbf{1}/\mathbf{4}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-642e342b173f9c41e1e70f8fabe35160_l3.png)
. Find: (i) ![Rendered by QuickLaTeX.com \[\mathbf{P}\left( \mathbf{A}|\mathbf{B} \right)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-437326d72ca9d40fee555f188950008d_l3.png)
(ii) ![Rendered by QuickLaTeX.com \[\mathbf{P}\left( \mathbf{B}|\mathbf{A} \right)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-22585687a92885988b9131abed2c4ed2_l3.png)
(iii) ![Rendered by QuickLaTeX.com \[\mathbf{P}\left( \mathbf{A}|\mathbf{B} \right)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-437326d72ca9d40fee555f188950008d_l3.png)
(iv) ![Rendered by QuickLaTeX.com \[\mathbf{P}\left( \mathbf{A}|\mathbf{B} \right)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-437326d72ca9d40fee555f188950008d_l3.png)
Given, P(A) = \[1/2\], P(B) = \[1/3\] and \[\mathbf{P}\left( \mathbf{A}\text{ }\mathbf{}\text{ }\mathbf{B} \right)\text{ }=\text{ }\mathbf{1}/\mathbf{4}\] \[P\left( A \right)\text{ }=\text{ }1\text{...
Explain why the experiment of tossing a coin three times is said to have binomial distribution.
As the random variable X takes \[0,1,2,3,......n\] is said to be binomial distribution having parameters n and p, if the probability is given by P(X = r) = \[^{n}{{C}_{r~}}{{p}^{r~}}{{q}^{n-r}}\]...
Two dice are thrown together and the total score is noted. The events E, F and G are ‘a total of ![Rendered by QuickLaTeX.com \[4\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3c0fa656ae249b0b1e03c8cd2e7be583_l3.png)
’, ‘a total of ![Rendered by QuickLaTeX.com \[9\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-eda27e23820084685a09a6f91d2210f2_l3.png)
or more’, and ‘a total divisible by ![Rendered by QuickLaTeX.com \[5\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7dc8465919d0838925dbc6c99670258c_l3.png)
’, respectively. Calculate P(E), P(F) and P(G) and decide which pairs of events, if any, are independent.
If two dice are thrown together, we have n(S) = \[36\] Now, let’s consider: E = A total of \[4\text{ }=\text{ }\left\{ \left( 2,\text{ }2 \right),\text{ }\left( 1,\text{ }3 \right),\text{ }\left(...
A bag contains ![Rendered by QuickLaTeX.com \[5\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7dc8465919d0838925dbc6c99670258c_l3.png)
red marbles and ![Rendered by QuickLaTeX.com \[3\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-df8bcc09db12acd0f6bda88b4b8135fb_l3.png)
black marbles. Three marbles are drawn one by one without replacement. What is the probability that at least one of the three marbles drawn be black, if the first marble is red?
Let red marbles be presented with R and black marble with B. Also, let E be the event that at least one of the three marbles drawn be black when the first marble is red. Now, the following three...
The probability that at least one of the two events A and B occurs is ![Rendered by QuickLaTeX.com \[0.6\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-de0b0f4aafc8e385df0d7807e1843841_l3.png)
. If A and B occur simultaneously with probability ![Rendered by QuickLaTeX.com \[0.3\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-eff452d0416dff35dab7d7d6ae2a8d4c_l3.png)
, evaluate ![Rendered by QuickLaTeX.com \[P(\overline{A})+P(\overline{B})\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-311b0ebecaf58a7477dc7c2516ef1eca_l3.png)
W.k.t, \[A\cup B\] denotes that atleast one of the events occurs and \[A\cap B\] denotes that two events occur simultaneously. Therefore, the required answer is \[1.1\].
Refer to Exercise 1 above. If the die were fair, determine whether or not the events A and B are independent.
According to the solution of exercise 1, we have \[A\text{ }=\text{ }\left\{ \left( 1,\text{ }1 \right),\text{ }\left( 2,\text{ }2 \right),\text{ }\left( 3,\text{ }3 \right),\text{ }\left( 4,\text{...
For a loaded die, the probabilities of outcomes are given as under: ![Rendered by QuickLaTeX.com \[\mathbf{P}\left( \mathbf{1} \right)\text{ }=\text{ }\mathbf{P}\left( \mathbf{2} \right)\text{ }=\text{ }\mathbf{0}.\mathbf{2},\text{ }\mathbf{P}\left( \mathbf{3} \right)\text{ }=\text{ }\mathbf{P}\left( \mathbf{5} \right)\text{ }=\text{ }\mathbf{P}\left( \mathbf{6} \right)\text{ }=\text{ }\mathbf{0}.\mathbf{1}\text{ }\mathbf{and}\text{ }\mathbf{P}\left( \mathbf{4} \right)\text{ }=\text{ }\mathbf{0}.\mathbf{3}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-4174be6da398129f0164c8571610db50_l3.png)
. The die is thrown two times. Let A and B be the events, ‘same number each time’, and ‘a total score is ![Rendered by QuickLaTeX.com \[10\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7e13914576c8f07fa7780b4b1aae684d_l3.png)
or more’, respectively. Determine whether or not A and B are independent.
Given that a loaded die is thrown such that \[\mathbf{P}\left( \mathbf{1} \right)\text{ }=\text{ }\mathbf{P}\left( \mathbf{2} \right)\text{ }=\text{ }\mathbf{0}.\mathbf{2},\text{ }\mathbf{P}\left(...
Show that the line through the points (4, 7, 8), (2, 3, 4) is parallel to the line through the points (–1, –2, 1), (1, 2, 5).
Solution: The points $(4,7,8),(2,3,4)$ and $(-1,-2,1),(1,2,5)$. Consider $A B$ be the line joining the points, $(4,7,8),(2,3,4)$ and $C D$ be the line through the points $(-1,-2$, 1), $(1,2,5)$. So...
A certain mass of hydrogen is changed to Helium by the process of fusion. The mass defect in fusion reaction is 0.02866 u. The energy liberated per u is: (given 1u = 931 MeV)
Option A 13.35 MeV Option B 2.67 MeV Option C 26.7 MeV Option D 6.675 MeV Solution: The correct option is Option D The energy released per u is given by:
In a common emitter (CE) amplifier having a voltage gain G, transistor used has trans conductance 0.02 mho and current gain 20, the voltage gain will be
Option A 5/4 G Option B 2/3 G Option C 1.5 G Option D 1/3 G Solution: The correct answer is Option B 2/3G
In Young’s double slit experiment, the slits are 2mm apart and are illuminated by photons of two wavelength λ1 = 12000 Å and λ2 = 10000 Å. At what minimum distance from the common central bright fringe on the screen 2m from the slit will a bright fringe from one interference pattern coincide with a bright fringe from the other?
Option A 3 mm Option B 8 mm Option C 6 mm Option D 4 mm Solution: The correct option is Option C Explanation: According to question, we have n1λ1 = n2λ2 $ \frac{{{\lambda }_{1}}}{{{\lambda...
Integrate the function in 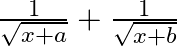
As per the given question, Let I = = = = = = = = =
Phosphorus forms a number of oxoacids. Out of these oxoacidsphosphinicacid has strong reducing property. Write its structure and also write a reaction showing its reducing behaviour.
Reactions Involved: 4AgNO3 + H3PO2 + 2H2O → 4Ag + H3PO4 + 4HNO3 2HgCl2 + H3PO2 + 2H2O → 2Hg + H3PO4 + 4HCl
PCl5 reacts with finely divided silver on heating and a white silver salt is obtained, which dissolves on adding excess aqueous NH3 solution. Write the reactions involved to explain what happens.
PCl5 reacts with silver to form white silver salt(AgCl). Which than dissolves on adding excess aqueous NH3 to form a soluble complex Reaction Involved: PCl5 + 2Ag → 2AgCl(white ppt.) + PCl3 AgCl +...
Phosphorus has three allotropic forms — (i) white phosphorus (ii) red phosphorus and (iii) black phosphorus. Write the difference between white and red phosphorus on the basis of their structure and reactivity.
White phosphorus 1. It is soft waxy solid having garlic order 2. It is poisonous 3. Has low melting point and boiling point because P4 molecules are held together by weak van der Waal forces of...
Nitric acid forms an oxide of nitrogen on reaction with P4O10. Write the reaction involved. Also, write the resonating structures of the oxide of nitrogen formed.
Reaction Involved: P4O10 + 4HNO3 → 4HPO3 + 2N2O5 White phosphorous is very reactive as compared to red phosphorous due to angular strain in white phosphorous.
Name three oxoacids of nitrogen. Write the disproportionation reaction of that oxoacid of nitrogen in which nitrogen is in +3 oxidation state.
Three oxoacids of nitrogen: 1.Nitric acid(HNO3) 2.Nitrous acid (HNO2) 3.Hyponitrous acid (H2N2O1) + 3 oxidation is shown by HNO2, Therefore it undergoes disproportion reaction, Calculation:...
P4O6 reacts with water according to equation P4O6 + 6H2O → 4H3PO3. Calculate the volume of 0.1 M NaOH solution required to neutralise the acid formed by dissolving 1.1 g of P4O6 in H2O.
Calculation: P4O6 + 6H2O → 4H3PO3 4H3PO3 + 8NaOH → Na2HPO3 + 8H20 P4O6 + 8NaOH → 4Na2HPO3 + 2H2O Moles of P4O6 = 1.1/220 = 0.5 Acid formed by one mole of P4o6 requires = 8 mol Acid formed by 0.005...
White phosphorus reacts with chlorine and the product hydrolyses in the presence of water. Calculate the mass of HCl obtained by the hydrolysis of the product formed by the reaction of 62 g of white phosphorus with chlorine in the presence of water.
Calculation: When white phosphorous reacts with chlorine: P4 + 6Cl2 → 4PCl3 PCl3 + 3H2O → H3PO3 + 4HCl ]*4 P4 +6Cl2 +12H2O → 4H3PO3 +12HCl Moles of white P= 62/124 = 0.5mol 1mol of white P4 produces...
Give an example to show the effect of concentration of nitric acid on the formation of oxidation product.
Example Reactions: 1. 4Zn +10HNO3(dil) → 4Zn(NO3)2 + NH4NO3 + 3H2O 2. 4Zn +10HNO3(dil) → 4Zn(NO3)2 + N2O + 5H2O 3. 4Zn +4HNO3(conc.) → Zn(NO3)2 + NO2 + 2H2O
A manufacturer produces two Models of bikes – Model X and Model Y. Model X takes ![Rendered by QuickLaTeX.com \[6\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-dba464f544e5646eaa291e02993dca75_l3.png)
man-hours to make per unit, while Model Y takes ![Rendered by QuickLaTeX.com \[10\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7e13914576c8f07fa7780b4b1aae684d_l3.png)
man-hours per unit. There is a total of ![Rendered by QuickLaTeX.com \[450\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-0308528700ef79a52f9e9df222e6aef8_l3.png)
man-hour available per week. Handling and Marketing costs are Rs ![Rendered by QuickLaTeX.com \[2000\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f1d2240de6dcb447376df455f7650d37_l3.png)
and Rs ![Rendered by QuickLaTeX.com \[1000\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-19afebc5b07af7e6daa7a65dc0d832c8_l3.png)
per unit for Models X and Y respectively. The total funds available for these purposes are Rs 80,000 per week. Profits per unit for Models X and Y are Rs ![Rendered by QuickLaTeX.com \[1000\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-19afebc5b07af7e6daa7a65dc0d832c8_l3.png)
and Rs ![Rendered by QuickLaTeX.com \[500\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-6ab5d1c783918e412f33f2a0d6a52a71_l3.png)
, respectively. How many bikes of each model should the manufacturer produce so as to yield a maximum profit? Find the maximum profit.
Let’s take x an y to be the number of models of bike produced by the manufacturer. From the question we have, Model x takes \[6\] man-hours to make per unit Model y takes \[10\] man-hours to make...
Maximize Z = x + y subject to ![Rendered by QuickLaTeX.com \[x~+\text{ }\mathbf{4}y~\text{£}\text{ }\mathbf{8},\text{ }\mathbf{2}x~+\text{ }\mathbf{3}y~\text{£}\text{ }\mathbf{12},\text{ }\mathbf{3}x~+~y~\text{£}\text{ }\mathbf{9},~x~{}^\text{3}\text{ }\mathbf{0},~y~{}^\text{3}\text{ }\mathbf{0}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-979bb74f9bdb51824148746fc9c40530_l3.png)
.
Given: Z = x + y subject to constraints, \[x~+\text{ }\mathbf{4}y~\text{£}\text{ }\mathbf{8},\text{ }\mathbf{2}x~+\text{ }\mathbf{3}y~\text{£}\text{ }\mathbf{12},\text{...
Refer to Exercise 15. Determine the maximum distance that the man can travel.
As per the solution of exercise 15, we have Maximize Z = x + y, subject to the constraints \[2x\text{ }+\text{ }3y\le 120\] … (i) \[8x\text{ }+\text{ }5y\le 400\]… (ii) \[x\ge 0,\text{ }y\ge 0\]...
Refer to Exercise 14. How many sweaters of each type should the company make in a day to get a maximum profit? What is the maximum profit?
As per the solution of exercise 14, we have Maximize \[Z\text{ }=\text{ }200x\text{ }+\text{ }120y\]subject to constrains \[3x\text{ }+\text{ }y\le 600\]…. (i) \[x\text{ }+\text{ }y\le 300\]…. (ii)...
Refer to Exercise 13. Solve the linear programming problem and determine the maximum profit to the manufacturer.
From the solution of exercise 13, we have The objective function for maximum profit \[Z\text{ }=\text{ }100x\text{ }+\text{ }170y\] Subject to constraints, \[x\text{ }+\text{ }4y\le 1800\]…. (i)...
Refer to Exercise 12. What will be the minimum cost?
As per the solution of exercise 12, we have The objective function for minimum cost is \[Z\text{ }=\text{ }400x\text{ }+\text{ }200y\] Subject to the constrains; \[5x\text{ }+\text{ }2y\ge 30\]….....
Refer to Exercise ![Rendered by QuickLaTeX.com \[11\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-96e5a16879d8a87c78503796e9403d2d_l3.png)
. How many of circuits of Type A and of Type B, should be produced by the manufacturer so as to maximize his profit? Determine the maximum profit.
As per the solution of exercise \[11\], we have Maximize \[Z\text{ }=\text{ }50x\text{ }+\text{ }60y\]subject to the constraints \[20x\text{ }+\text{ }10y\le 200\text{ }2x\text{ }+\text{ }y\le 20\]…...
A man rides his motorcycle at the speed of ![Rendered by QuickLaTeX.com \[50\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-fa087692b0efd2ba09c9cde470939182_l3.png)
km/hour. He has to spend Rs ![Rendered by QuickLaTeX.com \[2\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b1e8e3db630df9050b1fec3c4066d5e6_l3.png)
per km on petrol. If he rides it at a faster speed of ![Rendered by QuickLaTeX.com \[80\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f84c560175bb710101068599bb5acb81_l3.png)
km/hour, the petrol cost increases to Rs ![Rendered by QuickLaTeX.com \[3\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-df8bcc09db12acd0f6bda88b4b8135fb_l3.png)
per km. He has at most Rs ![Rendered by QuickLaTeX.com \[120\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-8c84a2d0bd88b31549ed72e8de4a263d_l3.png)
to spend on petrol and one hour’s time. He wishes to find the maximum distance that he can travel. Express this problem as a linear programming problem.
Let’s assume the man covers x km on his motorcycle at the speed of \[50\]km/hr and covers y km at the speed of \[50\] km/hr and covers y km at the speed of \[80\] km/hr. So, cost of petrol =...
A company manufactures two types of sweaters: type A and type B. It costs Rs ![Rendered by QuickLaTeX.com \[360\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-329b90b43e581de80754c8eba2a076da_l3.png)
to make a type A sweater and Rs ![Rendered by QuickLaTeX.com \[120\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-8c84a2d0bd88b31549ed72e8de4a263d_l3.png)
to make a type B sweater. The company can make at most ![Rendered by QuickLaTeX.com \[300\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-9c3d8595b36501ec206104d42324e4cb_l3.png)
sweaters and spend at most Rs ![Rendered by QuickLaTeX.com \[72000\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c29a9684313cc20ac3f22eaecee4193b_l3.png)
a day. The number of sweaters of type B cannot exceed the number of sweaters of type A by more than 100. The company makes a profit of Rs ![Rendered by QuickLaTeX.com \[200\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-47de0340997021e8e3902de17401f60e_l3.png)
for each sweater of type A and Rs ![Rendered by QuickLaTeX.com \[120\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-8c84a2d0bd88b31549ed72e8de4a263d_l3.png)
for every sweater of type B. Formulate this problem as a LPP to maximize the profit to the company.
Let’s assume x and y to be the number of sweaters of type A and type B respectively. From the question, the following constraints are: \[360x\text{ }+\text{ }120y\le 72000\Rightarrow 3x\text{...
A company manufactures two types of screws A and B. All the screws have to pass through a threading machine and a slotting machine. A box of Type A screws requires ![Rendered by QuickLaTeX.com \[2\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b1e8e3db630df9050b1fec3c4066d5e6_l3.png)
minutes on the threading machine and ![Rendered by QuickLaTeX.com \[3\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-df8bcc09db12acd0f6bda88b4b8135fb_l3.png)
minutes on the slotting machine. A box of type B screws requires ![Rendered by QuickLaTeX.com \[8\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-5ba6e07885b354f6c76c81fbd23c392a_l3.png)
minutes of threading on the threading machine and ![Rendered by QuickLaTeX.com \[2\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b1e8e3db630df9050b1fec3c4066d5e6_l3.png)
minutes on the slotting machine. In a week, each machine is available for ![Rendered by QuickLaTeX.com \[60\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-9b2a2573df8a14cd383c4547106574c4_l3.png)
hours. On selling these screws, the company gets a profit of Rs ![Rendered by QuickLaTeX.com \[100\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a40261fc9a48539be6f3f3cac1241623_l3.png)
per box on type A screws and Rs 170 per box on type B screws. Formulate this problem as a LPP given that the objective is to maximize profit.
Let’s consider that the company manufactures x boxes of type A screws and y boxes of type B screws. From the given information the below table is constructed: From the data in the above table, the...
A firm has to transport ![Rendered by QuickLaTeX.com \[1200\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a291b4fc34572f35be762f62f44244d6_l3.png)
packages using large vans which can carry ![Rendered by QuickLaTeX.com \[200\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-47de0340997021e8e3902de17401f60e_l3.png)
packages each and small vans which can take ![Rendered by QuickLaTeX.com \[80\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f84c560175bb710101068599bb5acb81_l3.png)
packages each. The cost for engaging each large van is Rs ![Rendered by QuickLaTeX.com \[400\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f2f3849d6e11b94c00641998e320efbf_l3.png)
and each small van is Rs ![Rendered by QuickLaTeX.com \[200\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-47de0340997021e8e3902de17401f60e_l3.png)
. Not more than Rs ![Rendered by QuickLaTeX.com \[3000\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-38a530e94753e67a9a2398736eb825ed_l3.png)
is to be spent on the job and the number of large vans cannot exceed the number of small vans. Formulate this problem as a LPP given that the objective is to minimize cost.
Let us consider x and y to be the number of large and small vans respectively. From the given information the below constrains table is constructed: Now, the objective function for minimum cost is...
A manufacturer of electronic circuits has a stock of ![Rendered by QuickLaTeX.com \[200\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-47de0340997021e8e3902de17401f60e_l3.png)
resistors, ![Rendered by QuickLaTeX.com \[120\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-8c84a2d0bd88b31549ed72e8de4a263d_l3.png)
transistors and ![Rendered by QuickLaTeX.com \[150\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d9a7badcce601c3f0bb966ea459aea8a_l3.png)
capacitors and is required to produce two types of circuits A and B. Type A requires ![Rendered by QuickLaTeX.com \[20\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f909910e2f598933c23989d90a7a4169_l3.png)
resistors, ![Rendered by QuickLaTeX.com \[10\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7e13914576c8f07fa7780b4b1aae684d_l3.png)
transistors and ![Rendered by QuickLaTeX.com \[10\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7e13914576c8f07fa7780b4b1aae684d_l3.png)
capacitors. Type B requires ![Rendered by QuickLaTeX.com \[10\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7e13914576c8f07fa7780b4b1aae684d_l3.png)
resistors, ![Rendered by QuickLaTeX.com \[20\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f909910e2f598933c23989d90a7a4169_l3.png)
transistors and ![Rendered by QuickLaTeX.com \[30\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-42f01f219fd66a7db9f04955aaa03f94_l3.png)
capacitors. If the profit on type A circuit is Rs ![Rendered by QuickLaTeX.com \[50\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-fa087692b0efd2ba09c9cde470939182_l3.png)
and that on type B circuit is Rs ![Rendered by QuickLaTeX.com \[60\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-9b2a2573df8a14cd383c4547106574c4_l3.png)
, formulate this problem as a LPP so that the manufacturer can maximize his profit.
Let x units of type A and y units of type B electric circuits be produced by the manufacturer. From the given information the below table is constructed: Now, the total profit function in rupees...
In Fig. 12.11, the feasible region (shaded) for a LPP is shown. Determine the maximum and minimum value of ![Rendered by QuickLaTeX.com \[\mathbf{Z}\text{ }=~x~+\text{ }\mathbf{2}y\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b80ed52b8ae39a40c6089b682f75c471_l3.png)
From the given figure, it’s seen that the corner points are as follows: \[R\left( 7/2,\text{ }3/4 \right),\text{ }Q\left( 3/2,\text{ }15/4 \right),\text{ }P\left( 3/13,\text{ }24/13 \right)\text{...
The feasible region for a LPP is shown in Fig. 12.10. Evaluate ![Rendered by QuickLaTeX.com \[\mathbf{Z}\text{ }=\text{ }\mathbf{4}x~+~y\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-552a20e496431cb5a75822a3ece9d00c_l3.png)
at each of the corner points of this region. Find the minimum value of Z, if it exists.
According to the question: \[\mathbf{Z}\text{ }=\text{ }\mathbf{4}x~+~y\] In the given figure, ABC is the feasible region which is open unbounded. Here, we have \[x\text{ }+\text{ }y\text{ }=\text{...
Refer to Exercise 7 above. Find the maximum value of Z.
In the evaluating table for the value of Z, it’s clearly seen that the maximum value of Z is \[47\] at \[(3,2)\]
The feasible region for a LPP is shown in Fig. 12.9. Find the minimum value of ![Rendered by QuickLaTeX.com \[\mathbf{Z}\text{ }=\text{ }\mathbf{11}x~+\text{ }\mathbf{7}y\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-5c7a02563203520b7505fe3ddb709e9f_l3.png)
.
In the given figure, it’s seen that the feasible region is ABCA. The corner points are \[C\left( 0,\text{ }3 \right),\text{ }B\left( 0,\text{ }5 \right)\]’and for A, we have to solve equations...
Feasible region (shaded) for a LPP is shown in Fig. 12.8. Maximize ![Rendered by QuickLaTeX.com \[\mathbf{Z}\text{ }=\text{ }\mathbf{5}x~+\text{ }\mathbf{7}y\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-55e25535c515d2a5fba086ba449805a2_l3.png)
.
According to the question: \[\mathbf{Z}\text{ }=\text{ }\mathbf{5}x~+\text{ }\mathbf{7}y\] and feasible region OABC. The corner points of the feasible region are \[O\left( 0,\text{ }0 \right),\text{...
Determine the maximum value of ![Rendered by QuickLaTeX.com \[\mathbf{Z}\text{ }=\text{ }\mathbf{3}x~+\text{ }\mathbf{4}y~\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-390dc45e23eba82376da394c50e1be8b_l3.png)
if the feasible region (shaded) for a LPP is shown in Fig. ![Rendered by QuickLaTeX.com \[12.7\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-5fe0cf8f8be924ed4a03666bcb48e81e_l3.png)
.
As shown in the figure, OAED is the feasible region. At A, \[y\text{ }=\text{ }0\]in equation \[2x\text{ }+\text{ }y\text{ }=\text{ }104\]we get, \[x=52\] This is a corner point \[A\text{ }=\text{...
Minimize ![Rendered by QuickLaTeX.com \[\mathbf{Z}\text{ }=\text{ }\mathbf{13}x~\text{ }\mathbf{15}y~\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-338f18452f410c945d5cabf1924ea645_l3.png)
subject to the constraints: ![Rendered by QuickLaTeX.com \[x~+~y~\text{£}\text{ }\mathbf{7},\text{ }\mathbf{2}x~\text{ }\mathbf{3}y~+\text{ }\mathbf{6}\text{ }{}^\text{3}\text{ }\mathbf{0},~x~{}^\text{3}\text{ }\mathbf{0},~y~{}^\text{3}\text{ }\mathbf{0}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-e55d23f4fcb872e75b4a8e7d4f615d75_l3.png)
.
According to the question: \[\mathbf{Z}\text{ }=\text{ }\mathbf{13}x~\text{ }\mathbf{15}y~\]and the constraints \[x~+~y~\text{£}\text{ }\mathbf{7},\text{ }\mathbf{2}x~\text{ }\mathbf{3}y~+\text{...
Maximize the function ![Rendered by QuickLaTeX.com \[\mathbf{Z}\text{ }=\text{ }\mathbf{11}x~+\text{ }\mathbf{7}y\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-5c7a02563203520b7505fe3ddb709e9f_l3.png)
, subject to the constraints: ![Rendered by QuickLaTeX.com \[x~\text{£}\text{ }\mathbf{3},~y~\text{£}\text{ }\mathbf{2},~x~{}^\text{3}\text{ }\mathbf{0},~y~{}^\text{3}\text{ }\mathbf{0}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-32897c7ada69b747fc2df4430eae78b1_l3.png)
.
According to the question: \[\mathbf{Z}\text{ }=\text{ }\mathbf{11}x~+\text{ }\mathbf{7}y\]and the constraints \[x~\text{£}\text{ }\mathbf{3},~y~\text{£}\text{ }\mathbf{2},~x~{}^\text{3}\text{...
Maximize ![Rendered by QuickLaTeX.com \[\mathbf{Z}\text{ }=\text{ }\mathbf{3}x~+\text{ }\mathbf{4}y\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-bb613b36107ec1e7348202194fd16fe6_l3.png)
, subject to the constraints: ![Rendered by QuickLaTeX.com \[x~+~y~\text{£}\text{ }\mathbf{1},~x~{}^\text{3}\text{ }\mathbf{0},~y~{}^\text{3}\text{ }\mathbf{0}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-8445e8a11a750a4c9e5f61100f78a870_l3.png)
.
According to the question: \[\mathbf{Z}\text{ }=\text{ }\mathbf{3}x~+\text{ }\mathbf{4}y\] and the constraints \[x~+~y~\text{£}\text{ }\mathbf{1},~x~{}^\text{3}\text{...
Determine the maximum value of ![Rendered by QuickLaTeX.com \[\mathbf{Z}\text{ }=\text{ }\mathbf{11}x~+\text{ }\mathbf{7}y~\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a04a1e74298ed4c91cc33f681051634b_l3.png)
subject to the constraints: ![Rendered by QuickLaTeX.com \[\mathbf{2}x~+~y~\text{£}\text{ }\mathbf{6},~x~\text{£}\text{ }\mathbf{2},~x~{}^\text{3}\text{ }\mathbf{0},~y~{}^\text{3}\text{ }\mathbf{0}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3bfc9eae4e5c2facd047b27f9d3525c4_l3.png)
.
According to the question: \[\mathbf{Z}\text{ }=\text{ }\mathbf{11}x~+\text{ }\mathbf{7}y~\]and the constraints \[\mathbf{2}x~+~y~\text{£}\text{ }\mathbf{6},~x~\text{£}\text{...
Choose the correct answer in 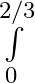 dx/4+9x^2 (A) pi/6 (B) pi/12 (C) pi/24 (D) pi/4
dx/4+9x^2 (A) pi/6 (B) pi/12 (C) pi/24 (D) pi/4
= = = = = = Therefore, The correct option is option (C) .
Dinucleotide is obtained by joining two nucleotides together by phosphodiester linkage. Between which carbon atoms of pentose sugars of nucleotides are Are these linkages present? (i) 5′ and 3′ (ii) 1′ and 5′ (iii) 5′ and 5′ (iv) 3′ and 3′
Option (i) is the answer. Between the pentose sugars of nucleotides, there are 5′ and 3′ connections.
Nucleic acids are the polymers of ______________. (i) Nucleosides (ii) Nucleotides (iii) Bases (iv) Sugars
Option (ii) is the answer. Nucleic acids are nucleotide polymers connected together by phosphodiester linkage.
Which of the following B group vitamins can be stored in our body? (i) Vitamin B1 (ii) Vitamin B2 (iii) Vitamin B6 (iv) Vitamin B12
Option (iv) is the answer. Because vitamin B12 is water insoluble, it can be stored in the body.
Carbohydrates are classified on the basis of their behaviour on hydrolysis and also as reducing or non-reducing sugar. Sucrose is a __________. (i) monosaccharide (ii) disaccharide (iii) reducing sugar (iv) non-reducing sugar
Option (ii) and (iv) are the answers. Sucrose is a non-reducing sugar and a disaccharide.
Monosaccharides contain carbonyl group hence are classified, as aldose or ketose. The number of carbon atoms present in the monosaccharide molecule is also considered for classification. In which class of monosaccharide will you place fructose?
Carbonyl groups can be found in monosaccharides. As a result, they're categorised as either aldose or ketose. Aldose refers to monosaccharides that contain an aldehyde group. Ketose refers to...
Aldopentoses named as ribose and 2-deoxyribose are found in nucleic acids. What is their relative configuration?
D-configuration is the configuration of both aldopentoses. -D-ribose is ribose, while -D-2-deoxyribose is 2-deoxyribose.
Structures of glycine and alanine are given below. Show the peptide linkage in glycylalanine.
Glycylalanine is formed when the hydroxyl group of glycine is bonded to the amine group of alanine via a peptide (-CONH) linkage.
The activation energy for the acid catalysed hydrolysis of sucrose is 6.22 kJ mol–1, while the activation energy is only 2.15 kJ mol–1 when hydrolysis is catalyzed by the enzyme sucrase. Explain.
Biocatalysts are enzymes. By providing an alternative approach, they lower the magnitude of activation energy. The enzyme sucrase lowers the activation energy of sucrose hydrolysis from 6.22 kJ...
Find the equation of the plane through the intersection of the planes r.(i+3j)-6=0 and r.(3i-j-4k)=0, whose perpendicular distance from origin is unity.
According to ques,
The plane ax + by = 0 is rotated about its line of intersection with the plane z = 0 through an angle α. Prove that the equation of the plane in its new position is Ax+by (
(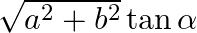 )z=0
)z=0
According to ques, planes are: \[~ax\text{ }+\text{ }by\text{ }=\text{ }0\text{ }\ldots .\text{ }\left( i \right)\] and \[z\text{ }=\text{ }0\text{ }\ldots .\text{ }\left( ii \right)\] hence, the...
Find the equation of the plane which is perpendicular to the plane 5x + 3y + 6z + 8 = 0 and which contains the line of intersection of the planes x + 2y + 3z – 4 = 0 and 2x + y – z + 5 = 0.
According to ques, planes are \[{{P}_{1}}:\text{ }5x\text{ }+\text{ }3y\text{ }+\text{ }6z\text{ }+\text{ }8\text{ }=\text{ }0\] \[{{P}_{2}}:\text{ }x\text{ }+\text{ }2y\text{ }+\text{ }3z\text{...
Find the shortest distance between the lines given by r=(8+3 ) i-(9+16 )j+(10=7 )k and r=15i+29j+5k+ (3i+8j-5k)
According to the ques,
Find the equation of the plane through the points (2, 1, –1) and (–1, 3, 4) and perpendicular to the plane x – 2y + 4z = 10. Solution:
According to ques, Equation of the plane passing through two points, \[\left( {{x}_{1}},\text{ }{{y}_{1}},\text{ }{{z}_{1}} \right)\text{ }and\text{ }\left( {{x}_{2}},\text{ }{{y}_{2}},\text{...
Find the equations of the line passing through the point (3,0,1) and parallel to the planes x + 2y = 0 and 3y – z = 0.
According to ques, Point is \[\left( 3,\text{ }0,\text{ }1 \right)\] and the equation of planes are: \[x\text{ }+\text{ }2y\text{ }=\text{ }0\text{ }\ldots .\text{ }\left( i \right)\] and \[3y\text{...
Evaluate the definite integrals as limit of sums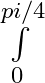 tanx dx
tanx dx
= = = = = =
Find the length and the foot of perpendicular from the point (1, 3/2, 2) to the plane 2x – 2y + 4z + 5 = 0.
According to ques, plane is: \[2x\text{ }\text{ }2y\text{ }+\text{ }4z\text{ }+\text{ }5\text{ }=\text{ }0\] and point: \[\left( 1,\text{ }3/2,\text{ }2 \right)\] The direction ratios of the...
Find the distance of a point (2, 4, –1) from the line (x+5)/1=(y+3)/4=(z-6)/-9
According to ques,
Find the foot of perpendicular from the point (2, 3, –8) to the line (4-x)/2=y/6=(1-z)/3 Also, find the perpendicular distance from the given point to the line.
according to ques, The coordinates of any point Q on the line are: \[x\text{ }=\text{ }-2\lambda \text{ }+\text{ }4,\text{ }y\text{ }=\text{ }6\lambda \text{ }and\text{ }z\text{ }=\text{ }-3\lambda...
Two systems of rectangular axis have the same origin. If a plane cuts them at distances a, b, c and a¢, b¢, c¢, respectively, from the origin, prove that I/a^2+1/b^2+1/c^2=1/a’^2+1/b’^2+1/c’^2
Let, \[~OX,\text{ }OY,\text{ }OZ\text{ }and\text{ }ox,\text{ }oy,\text{ }oz\] to be two rectangular systems According to ques,
O is the origin and A is (a, b, c). Find the direction cosines of the line OA and the equation of plane through A at right angle to OA.
According to ques, \[~O\text{ }\left( 0,\text{ }0,\text{ }0 \right)\text{ }and\text{ }A\left( a,\text{ }b,\text{ }c \right)\] Hence, the direction ratios of OA : \[a\text{ }\text{ }0,\text{ }b\text{...
If a variable line in two adjacent positions has direction cosines l, m, n and l + dl, m + dm, n + dn, show that the small angle dq between the two positions is given by dq2 = dl2 + dm2 + dn2
According to ques, \[~l,\text{ }m,\text{ }n\text{ }and~l~+\text{ }dl,~m~+\text{ }dm,~n~+\text{ }dn\] are the direction cosines of a variable line in two positions hence, \[{{l}^{2}}~+\text{...
Find the angle between the lines whose direction cosines are given by the equations l + m + n = 0, l2 + m2 – n2 = 0.
According to ques, Equations are, \[l~+~m~+~n~=\text{ }0\text{ }\ldots ..\text{ }\left( i \right)\] \[{{l}^{2}}~+~{{m}^{2}}~~{{n}^{2}}~=\text{ }0\text{ }\ldots .\text{ }\left( ii \right)\] From...
Find the equations of the two lines through the origin which intersect the line (x-3)/2=(y-3)/1=z/1 at angles of π/3 each.
According to ques, Any point in the given line is: \[x\text{ }\text{ }3/\text{ }2\text{ }=\text{ }y\text{ }\text{ }3/1\text{ }=\text{ }z/1\text{ }=\text{ }\lambda \] Or, \[x\text{ }=\text{ }2\lambda...
Find the equation of the plane through the points (2, 1, 0), (3, –2, –2) and (3, 1, 7).
According to ques, points are: \[\left( 2,\text{ }1,\text{ }0 \right),\text{ }\left( 3,\text{ }2,\text{ }2 \right)\text{ }and\text{ }\left( 3,\text{ }1,\text{ }7 \right)\] Since, equation of the...
If the line drawn from the point (–2, – 1, – 3) meets a plane at right angle at the point (1, – 3, 3), find the equation of the plane.
According to ques, Points are : \[\left( 2,\text{ }\text{ }1,\text{ }\text{ }3 \right)\text{ }and\text{ }\left( 1,\text{ }\text{ }3,\text{ }3 \right)\] And, Direction ratios of the normal to the...
Find the equation of a plane which is at a distance 3√3 units from origin and the normal to which is equally inclined to coordinate axis.
Since, the normal to the plane is equally inclined to the axes. so, \[cos\text{ }\alpha \text{ }=\text{ }cos\text{ }\beta \text{ }=\text{ }cos\text{ }\gamma \] or, \[So,\text{ }co{{s}^{2}}~\alpha...
Find the equation of a plane which bisects perpendicularly the line joining the points A (2, 3, 4) and B (4, 5, 8) at right angles.
According to ques, Coordinates are \[A\text{ }\left( 2,\text{ }3,\text{ }4 \right)\text{ }and\text{ }B\text{ }\left( 4,\text{ }5,\text{ }8 \right)\] Again, Coordinates of the mid-point C are...
Prove that the lines x = py + q, z = ry + s and x = p¢y + q¢, z = r¢y + s¢ are perpendicular if pp¢ + rr¢ + 1 = 0
According to ques,
Prove that the line through A (0, –1, –1) and B (4, 5, 1) intersects the line through C (3, 9, 4) and D (– 4, 4, 4).
According to ques, Points are \[~A\text{ }\left( 0,\text{ }1,\text{ }1 \right)\text{ }and\text{ }B\text{ }\left( 4,\text{ }5,\text{ }1 \right)\] \[C\text{ }\left( 3,\text{ }9,\text{ }4 \right)\text{...
Find the angle between the lines r=3i-2j+6k+ (2i+j+2k) and r=(2j-5k)+
(2i+j+2k) and r=(2j-5k)+ (6i+3j+2k)
(6i+3j+2k)
According to ques,
Show that the lines (x-1)/2=(y-2)/3=(z-3)/4 and (x-4)/5=(y-1)/2=z intersect. Also, find their point of intersection.
According to ques,
Find the vector equation of the line which is parallel to the vector 3i-2j+6k and which passes through the point (1, –2, 3).
According to equation of line we have,
Find the position vector of a point A in space such that vector OA is inclined at 60º to OX and at 45° to OY and vector OA = 10 units.
Since, \[co{{s}^{2}}~\alpha \text{ }+\text{ }co{{s}^{2}}~\beta \text{ }+\text{ }co{{s}^{2}}~\gamma \text{ }=\text{ }1\] or, \[co{{s}^{2}}~{{60}^{o}}~+\text{ }co{{s}^{2}}~{{45}^{o}}~+\text{...
The angle between two vectors a and b with magnitudes √3 and 4, respectively, and a.b=2×3^1/2 is
Solution: CORRECT OPTION: (B) as the ques suggests,
The vector having initial and terminal points as (2, 5, 0) and (–3, 7, 4), respectively is (A)-i+12j+4k (B)5i+2j-4k (C)-5i+2j+4k (D)i+j+k
CORRECT OPTION: \[\left( C \right)-5i+2j+4k\] Let us take, A and B be the pints with coordinates (2, 5, 0) and (-3, 7, 4) respectively. Hence,
The position vector of the point which divides the join of points 2a-3b and a+b in the ratio 3 : 1 is (A) (3a-2b)/2 (B) (7a-8b)/4 (C) 3a/4 (D) 5a/4
CORRECT ANSWER: \[\left( D \right)5a/4~\] ACCORDING TO QUES , Given ratio is 3:1
The vector in the direction of the vector i-2j+k that has magnitude 9 is (A) i-2j+2k (B)(i-2j+2k)/3 (C)3(i-2j+2k) (D)9(i-2j+2k)
CORRECT ANSWER: \[\left( C \right)\text{ }3\left( i-2j+2k \right)\]
If a=i+j+k and b=j-k, find a vector c such that axc=b and a.c=3
according to ques,
Show that area of the parallelogram whose diagonals are given by a and b is (axb)/2. Also find the area of the parallelogram whose diagonals are 2i-j+k and i+3j-k
according to ques,
If a,b,c determine the vertices of a triangle, show that ½[bxc+cxa+axb] gives the vector area of the triangle. Hence deduce the condition that the three points a,b,c are collinear. Also find the unit vector normal to the plane of the triangle.
according to ques,
Prove that in any triangle ABC, , where a, b, c are the magnitudes of the sides opposite to the vertices A, B, C, respectively.
according to ques,
Using vectors, prove that the parallelogram on the same base and between the same parallels are equal in area.
According to ques, proved.
Using vectors, find the area of the triangle ABC with vertices A(1, 2, 3), B(2, – 1, 4) and C(4, 5, – 1).
according to ques,
If A, B, C, D are the points with position vectors i+j-k, 2i-j+3k, 2i-3k, 3i-2j+k respectively, find the projection of AB along CD.
According to ques,
Find the sine of the angle between the vectors a=3i+j+2k and b=2i-2j+4k
according to ques,
If a+b+c=0 , show that axb=bxc=cxa . Interpret the result geometrically?
according to ques,
Find the angle between the vectors:2i-j+k and 3i+4j-k.
according to ques,
Find a vector of magnitude 6, which is perpendicular to both the vectors 2i-j+2k and 4i-j+3k .
according to ques,
A vector r has magnitude 14 and direction ratios 2, 3, – 6. Find the direction cosines and components of r , given that r makes an acute angle with x-axis.
According to ques,
A vector r is inclined at equal angles to the three axes. If the magnitude of r is 2√3 units, find r.
Since, vector makes equal angles with the axes, their direction cosines will be same hence, \[~l\text{ }=\text{ }m\text{ }=\text{ }n\] also, \[{{l}^{2}}~+\text{ }{{m}^{2}}~+\text{...
Using vectors, find the value of k such that the points (k, – 10, 3), (1, –1, 3) and (3, 5, 3) are collinear.
according to ques,
If a and b are the position vectors of A and B, respectively, find the position vector of a point C in BA produced such that BC = 1.5 BA.
According to ques,
Find a unit vector in the direction of PQ where P and Q have co-ordinates (5, 0, 8) and (3, 3, 2), respectively.
According to ques,
If a=i+j+2k and b=2i+j-2k find the unit vector in the direction of (i)6b (ii)2a-b
According to ques,
Find the unit vector in the direction of sum of vectors:
according to ques,
The differential equation for y = A cos αx + B sin αx, where A and B are arbitrary constants is (A)d2y/dx^2-a^2y=0 (B)d^2y/dx^2+a^2y=0 (C)d^2y/dx^2+ay=0 (D)d^2y/dx^2-ay=0
Correct option :(B) According to ques, \[y~=\text{ }A\text{ }cos\text{ }ax~+\text{ }B\text{ }sin\text{ }ax\] Differentiating with respect to x,
If y = e–x (A cos x + B sin x), then y is a solution of: (A) d^2y/dx^2+2dy/dx=0 (B)d^2y/dx^2-2dy/dx+2y=0 (C)d^2y/dx^2+2dy/dx=2y=0 (D)d^y/dx^2+2y=0
Correct option :(C). According to ques, \[y~=~{{e}^{x}}~\left( A\text{ }cos~x~+\text{ }B\text{ }sin~x \right)\] Differentiating both sides with respect to x,
The order and degree of the differential equation d^2y/dx^2=(dy/dx)^1/4+x^1/5=0 respectively, are (A) 2 and not defined (B) 2 and 2 (C) 2 and 3 (D) 3 and 3
Correct option : (A) 2 and not defined According to ques, Since the degree of dy/dx is in fraction its undefined and the degree is \[2.\]
Choose the correct answer from the given four options: The degree of the differential equation [1+(dy/dx)^2]^3/2=d^2y/dx^2 is (A) 4 (B) 3/2 (C) not defined (D) 2
Correct option: D (2) According to ques, hence the answer is 2.
Choose the correct answer from the given four options. The degree of the differential equation (d^2y/dx^2)^2+(dy/dx)^2=xsin(dy/dx)is: (A) 1 (B) 2 (C) 3 (D) not defined
Correct option: (D) not defined. As the value of sin (dy/dx) on expansion will be in increasing power of dy/dx,
Solve : x dy/dx (log y-logx+1)
According to ques,
Find the equation of a curve passing through the point (1, 1). If the tangent drawn at any point P (x, y) on the curve meets the co-ordinate axes at A and B such that P is the mid-point of AB.
Let \[P\left( x\text{ },\text{ }y \right)\] be any point on the curve, AB be the tangent to the given curve at P. A/Q, P is the mid-point of AB HENCE, the coordinates of \[A\text{ }is\text{ }\left(...
Find the equation of a curve passing through origin if the slope of the tangent to the curve at any point (x, y) is equal to the square of the difference of the abscissa and ordinate of the point.
According to the ques, The slope of the tangent of the curve \[=\text{ }dy/dx\] Now, the difference between the abscissa and ordinate \[=\text{ }x\text{ }\text{ }y\] Hence A/Q, \[dy/dx\text{...
Find the equation of the curve through the point (1, 0) if the slope of the tangent to the curve at any point (x, y) is (y – 1)/ (x2 + x)
According to ques, Since, the line is passing through the point (1, 0), then \[\left( 0\text{ }\text{ }1 \right)\text{ }\left( 1\text{ }+\text{ }1 \right)\text{ }=\text{ }c\left( 1...
Find the equation of the curve through the point (1, 0) if the slope of the tangent to the curve at any point (x, y) is (y – 1)/ (x2 + x)
ACCORDING TO QUES, Line is passing through the point \[\left( 1,\text{ }0 \right),SO,\] \[\left( 0\text{ }\text{ }1 \right)\text{ }\left( 1\text{ }+\text{ }1 \right)\text{ }=\text{ }c\left( 1...
Find the equation of a curve passing through (2, 1) if the slope of the tangent to the curve at any point (x, y) is (x2 + y2)/ 2xy.
ACCORDING TO QUES, It’s a homogeneous differential function,
Find the general solution of dy/dx – 3y = sin 2x.
According to ques, \[~P\text{ }=\text{ }-3\text{ }and\text{ }Q\text{ }=\text{ }sin\text{ }2x\]
Solve: dy/dx = cos(x + y) + sin (x + y). [Hint: Substitute x + y = z]
According to ques,
Find the general solution of (1 + tan y) (dx – dy) + 2xdy = 0.
according to ques,
Solve :
according to the ques,
Find the differential equation of system of concentric circles with centre (1, 2).
according to ques, concentric circles with centre \[\left( 1,\text{ }2 \right)\] and with radius ‘r’ can be written as, \[{{\left( x\text{ }\text{ }1 \right)}^{2}}~+\text{ }{{\left( y\text{ }\text{...
