Let’s take x an y to be the number of models of bike produced by the manufacturer.

From the question we have,

Model x takes

man-hours to make per unit

Model y takes

man-hours to make per unit

Total man-hours available =

So,

….. (i)

The handling and marketing cost of model x and y are Rs

and Rs

respectively.

And, the total funds available is Rs

per week

So,

… (ii)

And,

Now, the total profit (Z) per unit of models x and y are Rs

and Rs

repectively

⇒

Hence, the required LPP is

Maximize

subject to the constraints

Now, let’s construct a constrain table for the above:

Next, on solving equation (i) and (ii) we get

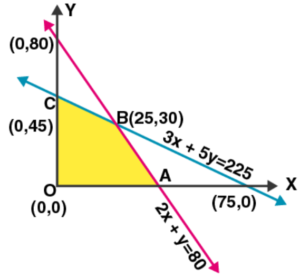
After plotting all the constraint equations, we observe that the feasible region is OABC, whose corner points are

On evaluating the value of Z, we get

Therefore, from the above table it’s seen that the maximum profit is Rs

.

The maximum profit can be achieved by producing

bikes of model x and

bikes of model Y or by producing

bikes of model x.