Answer: Consider, e be the identity element in I+ with respect to * a * e = a = e * a, ∀ a ∈ I+ a * e = a and e * a = a, ∀ a ∈ I+ a + e = a and e + a = a, ∀ a ∈ I+ e = 0, ∀ a ∈ I+ Hence, 0 is the...
Find the (v) length of the rectum of each of the following the hyperbola : ![Rendered by QuickLaTeX.com \[\frac{{{x}^{2}}}{25}-\frac{{{y}^{2}}}{4}=1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-79b83cfd05141077d859b528a32f1b5d_l3.png)
![Rendered by QuickLaTeX.com \[\frac{{{x}^{2}}}{25}-\frac{{{y}^{2}}}{4}=1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-79b83cfd05141077d859b528a32f1b5d_l3.png)
Given Equation: \[\frac{{{x}^{2}}}{25}-\frac{{{y}^{2}}}{4}=1\] Comparing with the equation of hyperbola \[\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{2}}}=1\] we get, a = 5 and b = 2 (v)...
Use king theorem of definite integral \[\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx\] \[y=\int _{0}^{\pi }\log (1+\cos (\pi -x))dx\] \[y=\int _{0}^{\pi }\log (1-\cos x)dx........(2)\] Adding...
Find the length of tangent drawn to a circle with radius 8 cm form a point 17 cm away from the center of the circle
Using properties of determinants prove that: 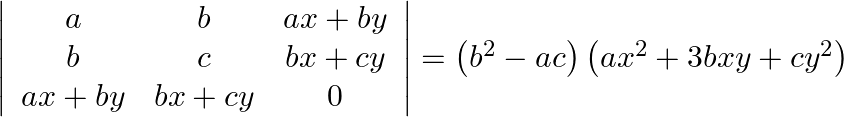
Solution: $\left|\begin{array}{ccc} a & b & a x+b y \\ b & c & b x+c y \\ a x+b y & b x+c y & 0 \end{array}\right|$ $\begin{array}{l} \left.=\left(\frac{1}{x...
Find the eccentricity of an ellipse whose latus rectum is one half of its major axis.
Find the eccentricity of an ellipse whose latus rectum is one half of its minor axis.
Find the equation of an ellipse whose eccentricity is ![Rendered by QuickLaTeX.com \[\frac{2}{3}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-047bcea7c848d7bdc13d26f95e67a4a4_l3.png)
, the latus rectum is ![Rendered by QuickLaTeX.com \[5\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7dc8465919d0838925dbc6c99670258c_l3.png)
, and the center is at the origin.
Find the equation of an ellipse, the lengths of whose major and mirror axes are ![Rendered by QuickLaTeX.com \[10\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7e13914576c8f07fa7780b4b1aae684d_l3.png)
and ![Rendered by QuickLaTeX.com \[8\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-5ba6e07885b354f6c76c81fbd23c392a_l3.png)
units respectively.
Find the equation of the ellipse which passes through the point ![Rendered by QuickLaTeX.com \[(4,1)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1ae2e4bedacd7350453509fb457a0319_l3.png)
and having its foci at ![Rendered by QuickLaTeX.com \[\left( \pm \mathbf{3},\text{ }\mathbf{0} \right)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-230cb6920566958d0c605f61419a7ed1_l3.png)
.
Find the equation of the ellipse with eccentricity ![Rendered by QuickLaTeX.com \[\frac{3}{4}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b506a58aabfe65c0a3f19affd6f9c8e7_l3.png)
, foci on the y-axis, center at the origin and passing through the point ![Rendered by QuickLaTeX.com \[(6,4)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-5d92f1e8ff96dfe442d91764fafe5723_l3.png)
.
Given Eccentricity = \[\frac{3}{4}\] We know that Eccentricity = c/a Therefore,c=\[\frac{3}{4}\]a
Find the equation of the ellipse with center at the origin, the major axis on the x-axis and passing through the points ![Rendered by QuickLaTeX.com \[\left( \mathbf{4},\text{ }\mathbf{3} \right)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-6e14255e5f2d2cbc940379e069bb5844_l3.png)
and ![Rendered by QuickLaTeX.com \[(-1,4)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-aeaab2e61affb979c28d3883772be7c5_l3.png)
.
Given: Center is at the origin and Major axis is along x – axis So, Equation of ellipse is of the form \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\]…(i) Given that ellipse passing...
Find the equation of the ellipse whose foci are at ![Rendered by QuickLaTeX.com \[\left( \mathbf{0},\text{ }\pm \mathbf{4} \right)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-bb2be58eb8036aac914c2c677f788949_l3.png)
and ![Rendered by QuickLaTeX.com \[e=\frac{4}{5}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c0fb8f8c87448e0d2f359f2d167e4c1a_l3.png)
![Rendered by QuickLaTeX.com \[e=\frac{4}{5}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c0fb8f8c87448e0d2f359f2d167e4c1a_l3.png)
Given: Coordinates of foci = \[\left( \mathbf{0},\text{ }\pm \mathbf{4} \right)\] …(i) We know that, Coordinates of foci = \[\left( 0,\text{ }\pm c \right)\] …(ii) The coordinates of the foci are...
Find the equation of the ellipse whose foci are at ![Rendered by QuickLaTeX.com \[\left( \pm \mathbf{1},\text{ }\mathbf{0} \right)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-873e68902b5445bb221bebb969489511_l3.png)
and e=1/2
Let the equation of the required ellipse be \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\] Given: Coordinates of foci = \[\left( \pm 1,\text{ }0 \right)\] …(i) We know that,...
Find the equation of the ellipse whose foci are ![Rendered by QuickLaTeX.com \[\left( \pm \mathbf{2},\text{ }\mathbf{0} \right)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7120150033b6ca5ebc01c838e0e9b285_l3.png)
and the eccentricity is ![Rendered by QuickLaTeX.com \[\frac{1}{2}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-eca8ad2eb4fe01867f7756c04c9a2882_l3.png)
Let the equation of the required ellipse be Given: Coordinates of foci = \[\left( \pm 2,\text{ }0 \right)\]…(iii) We know that, Coordinates of foci = \[\left( \pm c,\text{ }0 \right)\]…(iv) ∴ From...
Find the equation of the ellipse the ends of whose major and minor axes are ![Rendered by QuickLaTeX.com \[\left( \pm \mathbf{4},\text{ }\mathbf{0} \right)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7e4c65ec2153cec645be0c25f93adce9_l3.png)
and ![Rendered by QuickLaTeX.com \[\left( \mathbf{0},\text{ }\pm \mathbf{3} \right)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2d6b922fc27485fd054fb582ccf195be_l3.png)
respectively.
Given: Ends of Major Axis = \[\left( \pm \mathbf{4},\text{ }\mathbf{0} \right)\] and Ends of Minor Axis = \[\left( \mathbf{0},\text{ }\pm \mathbf{3} \right)\] Here, we can see that the major axis is...
Find the equation of the ellipse whose vertices are the ![Rendered by QuickLaTeX.com \[(0,\pm 7)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-06930137911286949055c190e479f75e_l3.png)
and foci at ![Rendered by QuickLaTeX.com \[(0,\pm \sqrt{7})\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1992b2f60ca3bf6ba810d7743190c38a_l3.png)
.
Given: Vertices = \[(0,\pm 4)\] …(i) The vertices are of the form = (0, ±a) …(ii) Hence, the major axis is along y – axis ∴ From eq. (i) and (ii), we get \[\begin{array}{*{35}{l}} a\text{ }=\text{...
Find the equation of the ellipse whose vertices are at ![Rendered by QuickLaTeX.com \[\left( \pm \mathbf{6},\text{ }\mathbf{0} \right)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2a03fb4e270050a2606c20b670ee0466_l3.png)
and foci at ![Rendered by QuickLaTeX.com \[(\pm \mathbf{4},~\mathbf{0})\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-10ca5316ffee057110a312dedd039adb_l3.png)
.
Given: Vertices = \[\left( \pm \mathbf{6},\text{ }\mathbf{0} \right)\] …(i) The vertices are of the form = \[\left( \pm a,\text{ }0 \right)\] …(ii) Hence, the major axis is along x – axis ∴ From eq....
Find the (v) length of the latus rectum of each of the following ellipses. ![Rendered by QuickLaTeX.com \[\mathbf{25}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{4}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{100}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3badc0893d1a72abf2537d836a63e857_l3.png)
Given: \[\mathbf{25}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{4}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{100}\] Divide by \[100\] to both the sides, we get...
Find the (iii) coordinates of the foci, (iv) eccentricity ![Rendered by QuickLaTeX.com \[\mathbf{25}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{4}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{100}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3badc0893d1a72abf2537d836a63e857_l3.png)
Given: \[\mathbf{25}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{4}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{100}\] Divide by \[100\] to both the sides, we get...
Find the (iii) coordinates of the foci, (iv) eccentricity ![Rendered by QuickLaTeX.com \[\mathbf{16}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{16}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c1bda8518d8de0566fb7bb8dae83e7d6_l3.png)
Given: \[\mathbf{16}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{16}\] Divide by \[16\] to both the sides, we get...
Find the (i) lengths of major axes, (ii) coordinates of the vertices
Given: \[\mathbf{3}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{2}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{18}\]…(i) Divide by \[18\] to both the sides, we get...
Find the (v) length of the latus rectum of each of the following ellipses. ![Rendered by QuickLaTeX.com \[\frac{{{x}^{2}}}{9}+\frac{{{y}^{2}}}{16}=1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1f0a66ca234bf1c2806a47a69c3bf010_l3.png)
Answer :
![Rendered by QuickLaTeX.com \[\frac{{{x}^{2}}}{9}+\frac{{{y}^{2}}}{16}=1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1f0a66ca234bf1c2806a47a69c3bf010_l3.png)
Given: \[\frac{{{x}^{2}}}{9}+\frac{{{y}^{2}}}{16}=1\]….(i) Since, \[9<16\] So, above equation is of the form, \[\frac{{{x}^{2}}}{{{b}^{2}}}+\frac{{{y}^{2}}}{{{a}^{2}}}=1\]…(ii) Comparing eq. (i)...
Find the (iii) coordinates of the foci, (iv) eccentricity ![Rendered by QuickLaTeX.com \[\frac{{{x}^{2}}}{9}+\frac{{{y}^{2}}}{16}=1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1f0a66ca234bf1c2806a47a69c3bf010_l3.png)
![Rendered by QuickLaTeX.com \[\frac{{{x}^{2}}}{9}+\frac{{{y}^{2}}}{16}=1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1f0a66ca234bf1c2806a47a69c3bf010_l3.png)
Given: \[\frac{{{x}^{2}}}{9}+\frac{{{y}^{2}}}{16}=1\]….(i) Since, \[9<16\] So, above equation is of the form, \[\frac{{{x}^{2}}}{{{b}^{2}}}+\frac{{{y}^{2}}}{{{a}^{2}}}=1\]…(ii) Comparing...
Find the (i) lengths of major axes, (ii) coordinates of the vertices ![Rendered by QuickLaTeX.com \[\frac{{{x}^{2}}}{9}+\frac{{{y}^{2}}}{16}=1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1f0a66ca234bf1c2806a47a69c3bf010_l3.png)
![Rendered by QuickLaTeX.com \[\frac{{{x}^{2}}}{9}+\frac{{{y}^{2}}}{16}=1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1f0a66ca234bf1c2806a47a69c3bf010_l3.png)
Given: \[\frac{{{x}^{2}}}{9}+\frac{{{y}^{2}}}{16}=1\]….(i) Since, \[9<16\] So, above equation is of the form, \[\frac{{{x}^{2}}}{{{b}^{2}}}+\frac{{{y}^{2}}}{{{a}^{2}}}=1\]…(ii) Comparing eq. (i)...
Find the (v) length of the latus rectum of each of the following ellipses.
Given: \[\frac{{{x}^{2}}}{4}+\frac{{{y}^{2}}}{25}=1\]…(i) Since, \[4\text{ }<\text{ }25\] So, above equation is of the form, \[\frac{{{x}^{2}}}{{{b}^{2}}}+\frac{{{y}^{2}}}{{{a}^{2}}}=1\]…(ii)...
Find the (i) lengths of major axes, (ii) coordinates of the vertices ![Rendered by QuickLaTeX.com \[\frac{{{x}^{2}}}{4}+\frac{{{y}^{2}}}{25}=1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2cd71d027e4ee356834184fd92e4f618_l3.png)
![Rendered by QuickLaTeX.com \[\frac{{{x}^{2}}}{4}+\frac{{{y}^{2}}}{25}=1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2cd71d027e4ee356834184fd92e4f618_l3.png)
Given: \[\frac{{{x}^{2}}}{4}+\frac{{{y}^{2}}}{25}=1\]…(i) Since, \[4\text{ }<\text{ }25\] So, above equation is of the form, \[\frac{{{x}^{2}}}{{{b}^{2}}}+\frac{{{y}^{2}}}{{{a}^{2}}}=1\]…(ii)...
Find the (v) length of the latus rectum of each of the following ellipses. ![Rendered by QuickLaTeX.com \[\mathbf{4}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{9}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{1}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c30dd6bfab0df4e91e525631f2ba2f4a_l3.png)
Given: \[\mathbf{4}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{9}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{1}\] \[\frac{{{x}^{2}}}{\frac{1}{4}}+\frac{{{y}^{2}}}{\frac{1}{9}}=1\]….(i) Since,...
Find the (iii) coordinates of the foci, (iv) eccentricity ![Rendered by QuickLaTeX.com \[\mathbf{4}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{9}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{1}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c30dd6bfab0df4e91e525631f2ba2f4a_l3.png)
Given: \[\mathbf{4}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{9}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{1}\] \[\frac{{{x}^{2}}}{\frac{1}{4}}+\frac{{{y}^{2}}}{\frac{1}{9}}=1\]….(i) Since,...
Find the (i) lengths of major axes, (ii) coordinates of the vertices ![Rendered by QuickLaTeX.com \[\mathbf{4}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{9}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{1}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c30dd6bfab0df4e91e525631f2ba2f4a_l3.png)
Given: \[\mathbf{4}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{9}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{1}\] \[\frac{{{x}^{2}}}{\frac{1}{4}}+\frac{{{y}^{2}}}{\frac{1}{9}}=1\]….(i) Since, ...
Find the (v) length of the latus rectum of each of the following ellipses. ![Rendered by QuickLaTeX.com \[\mathbf{9}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{16}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{144}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-862342dfce29b8b9c9392c90bd44304d_l3.png)
Given: \[\mathbf{9}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{16}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{144}\] Divide by \[144\] to both the sides, we get...
Find the (iii) coordinates of the foci, (iv) eccentricity
Given: \[\mathbf{9}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{16}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{144}\] Divide by \[144\] to both the sides, we get...
Find the (i) lengths of major axes, (ii) coordinates of the vertices ![Rendered by QuickLaTeX.com \[\mathbf{9}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{16}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{144}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-862342dfce29b8b9c9392c90bd44304d_l3.png)
Given: \[\mathbf{9}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{16}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{144}\] Divide by \[144\] to both the sides, we get...
Find the (v) length of the latus rectum of each of the following ellipses. ![Rendered by QuickLaTeX.com \[{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{4}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{100}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b1c4d22d5b39a8859feb9ee71c371bb0_l3.png)
Given \[{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{4}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{100}\] Divide by \[100\] to both the sides, we get...
Find the (iii) coordinates of the foci, (iv) eccentricity ![Rendered by QuickLaTeX.com \[{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{4}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{100}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b1c4d22d5b39a8859feb9ee71c371bb0_l3.png)
Given \[{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{4}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{100}\] Divide by \[100\] to both the sides, we get...
Find the (i) lengths of major axes, (ii) coordinates of the vertices ![Rendered by QuickLaTeX.com \[{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{4}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{100}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b1c4d22d5b39a8859feb9ee71c371bb0_l3.png)
Given \[{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{4}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{100}\] Divide by \[100\] to both the sides, we get...
Find the (v) length of the latus rectum of each of the following ellipses. ![Rendered by QuickLaTeX.com \[\mathbf{16}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{25}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{400}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-aed3022a6a6b09b7823a798e1b61f3a4_l3.png)
Given: \[\mathbf{16}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{25}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{400}\] Divide by \[400\] to both the sides, we get...
Find the (iii) coordinates of the foci, (iv) eccentricity ![Rendered by QuickLaTeX.com \[\mathbf{16}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{25}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{400}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-aed3022a6a6b09b7823a798e1b61f3a4_l3.png)
Given: \[\mathbf{16}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{25}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{400}\] Divide by \[400\] to both the sides, we get...
Find the (i) lengths of major axes, (ii) coordinates of the vertices ![Rendered by QuickLaTeX.com \[\mathbf{16}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{25}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{400}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-aed3022a6a6b09b7823a798e1b61f3a4_l3.png)
Given: \[\mathbf{16}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{25}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{400}\] Divide by \[400\] to both the sides, we get...
Find the (v) length of the latus rectum of each of the following ellipses. ![Rendered by QuickLaTeX.com \[\frac{{{x}^{2}}}{49}+\frac{{{y}^{2}}}{36}=1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-07b8fa9753bba0be6e51668e79506671_l3.png)
![Rendered by QuickLaTeX.com \[\frac{{{x}^{2}}}{49}+\frac{{{y}^{2}}}{36}=1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-07b8fa9753bba0be6e51668e79506671_l3.png)
Given: \[\frac{{{x}^{2}}}{49}+\frac{{{y}^{2}}}{36}=1\]…(i) Since, \[49\text{ }>\text{ }36\] So, above equation is of the form, \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\] …(ii)...
Find the (i) lengths of major axes, (ii) coordinates of the vertices ![Rendered by QuickLaTeX.com \[\frac{{{x}^{2}}}{49}+\frac{{{y}^{2}}}{36}=1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-07b8fa9753bba0be6e51668e79506671_l3.png)
![Rendered by QuickLaTeX.com \[\frac{{{x}^{2}}}{49}+\frac{{{y}^{2}}}{36}=1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-07b8fa9753bba0be6e51668e79506671_l3.png)
Given: \[\frac{{{x}^{2}}}{49}+\frac{{{y}^{2}}}{36}=1\]…(i) Since, \[49\text{ }>\text{ }36\] So, above equation is of the form, \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\] …(ii)...
Find the(v) length of the latus rectum of each of the following ellipses. ![Rendered by QuickLaTeX.com \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d32e615a6517b76e65b04fd25ae8bf0a_l3.png)
![Rendered by QuickLaTeX.com \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d32e615a6517b76e65b04fd25ae8bf0a_l3.png)
Given: \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\]…(i) Since, \[25>9\] So, above equation is of the form, \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\]…(ii)...
Find the (i) lengths of major axes, (ii) coordinates of the vertices ![Rendered by QuickLaTeX.com \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d32e615a6517b76e65b04fd25ae8bf0a_l3.png)
![Rendered by QuickLaTeX.com \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d32e615a6517b76e65b04fd25ae8bf0a_l3.png)
Given: \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\]…(i) Since, \[25>9\] So, above equation is of the form, \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\]…(ii)...
If (1 + i)z = (1 – i) then prove that
A beam is supported at its ends by supports which are 12 m apart. Since the load is concentrated at its centre, there is a deflection of 3 cm at the centre, and the deflected beam is in the shape of a parabola. How far from the centre is the deflection 1 cm?
Given, A beam is supported at its ends by supports which are 12 m apart. There is a deflection of 3 cm at the centre, and the deflected beam is in the shape of a parabola. EF are the...
A rod of length 15 cm moves with its ends always touching the coordinate axes. Find the equation of the locus of a point P on the rod, which is at a distance of 3 cm from the end in contact with the x-axis.
Answer: Given, A rod of length 15 cm moves with its ends always touching the coordinate axes. A point P on the rod, which is at a distance of 3 cm from the end in contact with...
The towers of bridge, hung in the form of a parabola, have their tops 30 m above the roadway, and are 200 m apart. If the cable is 5 m above the roadway at the centre of the bridge, find the length of the vertical supporting cable, 30 m from the centre.
Answer: Given, Top of the towers are 30 m above the roadway and are 200 m apart. Cable is 5 m above the roadway at centre. A and B are the top of the towers. AE and BF are the...
A parabolic reflector is 5 cm deep and its diameter is 20 cm. How far is its focus from the vertex?
Answer: Given, Parabolic reflector = 5 cm deep Diameter = 20 cm Reflector is 5 cm deep, OD = 5 cm Diameter of the mirror is 20 com, BC = 20 cm The equation...
The focus of a parabolic mirror is at a distance of 6 cm from its vertex. If the mirror is 20 cm deep, find its diameter.
Answer: Given, The focus of a parabolic mirror is at a distance of 6 cm from its vertex. And the mirror is 20 cm deep. O is the vertex A is the Focus OA = a = 6...
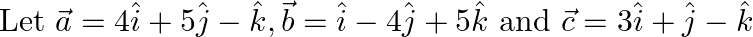 Find a vector
Find a vector 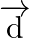 which is perpendicular to both
which is perpendicular to both 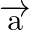 and
and 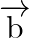 , and is such that
, and is such that 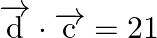 .
.
Solution: $\begin{array}{l} \vec{a}=4 \hat{\imath}+5 \hat{\jmath}-\hat{k} \\ \vec{b}=\hat{\imath}-4 \hat{\jmath}+5 \hat{k} \end{array}$ $\vec{c}=3 \hat{\imath}+\hat{\jmath}-\hat{k}$ Let...
Find the equation of the line passing through the intersection of the lines 3x – 4y + 1 = 0 and 5x + y – 1 = 0 and which cuts off equal intercepts from the axes.
Answer : Suppose the given two lines intersect at a point P(x1, y1). Then, (x1, y1) satisfies each of the given equations. 3x – 4y + 1 = 0 …(i) 5x + y – 1 = 0 …(ii) Now, we find the point of...
Find the equation of the line through the intersection of the lines 2x + 3y – 2 = 0 and x – 2y + 1 = 0 and having x-intercept equal to 3.
Answer : Suppose the given two lines intersect at a point P(x1, y1). Then, (x1, y1) satisfies each of the given equations. 2x + 3y – 2 = 0 …(i) x – 2y + 1 = 0 …(ii) Now, we find the point of...
Find the equation of the line through the intersection of the lines 2x – 3y + 1 = 0 and x + y – 2 = 0 and drawn parallel to y-axis.
Answer : Suppose the given two lines intersect at a point P(x1, y1). Then, (x1, y1) satisfies each of the given equations. 2x – 3y + 1 = 0 …(i) x + y – 2 = 0 …(ii) Now, we find the point of...
Find the equation of the line through the intersection of the lines x – 7y + 5 = 0 and 3x + y – 7 = 0 and which is parallel to x-axis.
Answer : Suppose the given two lines intersect at a point P(x1, y1). Then, (x1, y1) satisfies each of the given equations. x – 7y + 5 = 0 …(i) 3x + y – 7 = 0 …(ii) Now, we find the point of...
Find the equation of the line through the intersection of the lines 2x – 3y = 0 and 4x – 5y = 2 and which is perpendicular to the line x + 2y + 1 = 0.
Answer : Suppose the given two lines intersect at a point P(x1, y1). Then, (x1, y1) satisfies each of the given equations. 2x – 3y = 0 …(i) 4x – 5y = 2 …(ii) Now, we find the point of intersection...
Find the equation of the line through the intersection of the lines 5x – 3y = 1 and 2x + 3y = 23 and which is perpendicular to the line 5x – 3y = 1.
Answer : Suppose the given two lines intersect at a point P(x1, y1). Then, (x1, y1) satisfies each of the given equations. 5x – 3y = 1 …(i) 2x + 3y = 23 …(ii) Now, we find the point of intersection...
Find the equation of the line drawn through the point of intersection of the lines x – y = 1 and 2x – 3y + 1 = 0 and which is parallel to the line 3x + 4y = 12.
Answer : Suppose the given two lines intersect at a point P(x1, y1). Then, (x1, y1) satisfies each of the given equations. x – y = 1 …(i) 2x – 3y + 1 = 0 …(ii) Now, we find the point of intersection...
Find the equation of the line drawn through the point of intersection of the lines x + y = 9 and 2x – 3y + 7 = 0 and whose slope is −???? . ????
Answer : Suppose the given two lines intersect at a point P(x1, y1). Then, (x1, y1) satisfies each of the given equations. x + y = 9 …(i) 2x – 3y + 7 = 0 …(ii) Now, we find the point of intersection...
Find the equation of the line drawn through the point of intersection of the lines x – y = 7 and 2x + y = 2 and passing through the origin.
Answer : Suppose the given two lines intersect at a point P(x1, y1). Then, (x1, y1) satisfies each of the given equations. x – y = 7 …(i) 2x + y = 2 …(ii) Now, we find the point of intersection of...
Find the equation of the line drawn through the point of intersection of the lines x – 2y + 3 = 0 and 2x – 3y + 4 = 0 and passing through the point (4, -5).
Answer : Suppose the given two lines intersect at a point P(x1, y1). Then, (x1, y1) satisfies each of the given equations. x – 2y + 3 = 0 …(i) 2x – 3y + 4 = 0 …(ii) Now, we find the point of...
Transform the equation 2×2 + y2 – 4x + 4y = 0 to parallel axes when the origin is shifted to the point (1, -2).
Answer : Let the new origin be (h, k) = (1, -2) Then, the transformation formula become: x = X + 1 and y = Y + (-2) = Y – 2 Substituting the value of x and y in the given equation, we get 2x2 + y2 –...
Find what the given equation becomes when the origin is shifted to the point (1, 1). xy – x – y + 1 = 0
Answer : Let the new origin be (h, k) = (1, 1) Then, the transformation formula become: x = X + 1 and y = Y + 1 Substituting the value of x and y in the given equation, we get xy – x – y + 1 = 0...
Find what the given equation becomes when the origin is shifted to the point (1, 1)
x2 – y2 – 2x + 2y = 0 Answer : Let the new origin be (h, k) = (1, 1) Then, the transformation formula become: x = X + 1 and y = Y + 1 Substituting the value of x and y in the given equation, we get...
Find what the given equation becomes when the origin is shifted to the point (1, 1). xy – y2 – x + y = 0
Answer : Let the new origin be (h, k) = (1, 1) Then, the transformation formula become: x = X + 1 and y = Y + 1 Substituting the value of x and y in the given equation, we get xy – y2 – x + y = 0...
Find what the given equation becomes when the origin is shifted to the point (1, 1)
x2 + xy – 3x – y + 2 = 0 Answer : Let the new origin be (h, k) = (1, 1) Then, the transformation formula become: x = X + 1 and y = Y + 1 Substituting the value of x and y in the given equation, we...
At what point must the origin be shifted, if the coordinates of a point (-4,2) become (3, -2)?
Answer : Let (h, k) be the point to which the origin is shifted. Then, x = -4, y = 2, X = 3 and Y = -2 ∴ x = X + h and y = Y + k ⇒ -4 = 3 + h and 2 = -2 + k ⇒ h = -7 and k = 4 Hence, the origin must...
If the origin is shifted to the point (2, -1) by a translation of the axes, the coordinates of a point become (-3, 5). Find the origin coordinates of the point.
Answer : Let the new origin be (h, k) = (2, -1) and (x, y) = (-3, 5) be the given point. Let the new coordinates be (X, Y) We use the transformation formula: x = X + h and y = Y + k ⇒ -3 = X + 2 and...
If the origin is shifted to the point (0, -2) by a translation of the axes, the coordinates of a point become (3, 2). Find the original coordinates of the point.
Answer : Let the new origin be (h, k) = (0, -2) and (x, y) = (3, 2) be the given point. Let the new coordinates be (X, Y) We use the transformation formula: x = X + h and y = Y + k ⇒ 3 = X + 0 and 2...
If the origin is shifted to the point (-3, -2) by a translation of the axes, find the new coordinates of the point (3, -5).
Answer : Let the new origin be (h, k) = (-3, -2) and (x, y) = (3, -5) be the given point. Let the new coordinates be (X, Y) We use the transformation formula: x = X + h and y = Y + k ⇒ 3 = X – 3 and...
If the origin is shifted to the point (1, 2) by a translation of the axes, find the new coordinates of the point (3, -4).
Answer : Let the new origin be (h, k) = (1, 2) and (x, y) = (3, -4) be the given point. Let the new coordinates be (X, Y) We use the transformation formula: x = X + h and y = Y + k ⇒ 3 = X + 1 and...
Find the equations of the medians of a triangle whose sides are given by the equations 3x + 2y + 6 = 0, 2x – 5y + 4 = 0 and x -3y – 6 = 0.
Find the equation of the perpendicular drawn from the point P(-2, 3) to the line x– 4y + 7 = 0. Also, find the coordinates of the foot of the perpendicular.
Let the equation of line AB be x – 4y + 7 = 0 and point C be (-2, 3) CD is perpendicular to the line AB, and we need to find: Equation of Perpendicular drawn from point C Coordinates of D Let the...
Find the equation of the perpendicular drawn from the origin to the line 4x – 3y + 5 = 0. Also, find the coordinates of the foot of the perpendicular.
Let the equation of line AB be 4x – 3y + 5 = 0 and point C be (0, 0) CD is perpendicular to the line AB, and we need to find: Equation of Perpendicular drawn from point C Coordinates of D Let the...
Find the area of the triangle, the equations of whose sides are y = x, y = 2x and y – 3x = 4.
Answer : The given equations are y = x …(i) y = 2x …(ii) and y – 3x = 4 …(iii) Let eq. (i), (ii) and (iii) represents the sides AB, BC and AC respectively of ΔABC From eq. (i) and (ii), we get x = 0...
Find the area of the triangle formed by the lines x = 0, y = 1 and 2x + y = 2.
Answer : The given equations are x = 0 …(i) y = 1 …(ii) and 2x + y = 2 …(iii) Let eq. (i), (ii) and (iii) represents the sides AB, BC and AC respectively of ΔABC From eq. (i) and (ii), we get x = 0...
Find the area of the triangle formed by the lines x + y = 6, x – 3y = 2 and 5x – 3y + 2 = 0.
The given equations are x + y = 6 …(i) x – 3y = 2 …(ii) and 5x – 3y + 2 = 0 or 5x – 3y = -2 …(iii) Let eq. (i), (ii) and (iii) represents the sides AB, BC and AC respectively of ΔABC Firstly, we...
Find the image of the point P(1, 2) in the line x – 3y + 4 = 0.
Find the value of k so that the lines 3x – y – 2 = 0, 5x + ky – 3 = 0 and 2x + y – 3 = 0 are concurrent.
Answer : Given that 3x – y – 2 = 0, 5x + ky – 3 = 0 and 2x + y – 3 = 0 are concurrent We know that, The lines a1x + b1y + c1 = 0, a1x + b1y + c1 = 0 and a1x + b1y + c1 = 0 are concurrent if It is...
Show that the lines 3x – 4y + 5 = 0, 7x – 8y + 5 = 0 and 4x + 5y = 45 are concurrent. Also find their point of intersection.
Answer : Given: 3x – 4y + 5 = 0, 7x – 8y + 5 = 0 and 4x + 5y = 45 or 4x + 5y – 45 = 0 To show: Given lines are concurrent The lines a1x + b1y + c1 = 0, a1x + b1y + c1 = 0 and a1x + b1y + c1 = 0 are...
Show that the lines x + 7y = 23 and 5x + 2y = a 16 intersect at the point (2, 3).
Answer : Suppose the given two lines intersect at a point P(2, 3). Then, (2, 3) satisfies each of the given equations. So, taking equation x + 7y = 23 Substituting x = 2 and y = 3 Lhs = x + 7y = 2 +...
Find the points of intersection of the lines 4x + 3y = 5 and x = 2y – 7.
Answer : Suppose the given two lines intersect at a point P(x1, y1). Then, (x1, y1) satisfies each of the given equations. ∴ 4x + 3y = 5 or 4x + 3y – 5 = 0 …(i) and x = 2y – 7 or x – 2y + 7 = 0...
The perpendicular distance of a line from the origin is 5 units, and its slope is -1. Find the equation of the line.
Find the distance between the parallel lines p(x + y) = q = 0 and p(x + y) – r =0
Find the distance between the parallel lines y = mx + c and y = mx + d
Find the distance between the parallel lines 8x + 15y – 36 = 0 and 8x + 15y + 32 = 0.
Find the distance between the parallel lines 4x – 3y + 5 = 0 and 4x – 3y + 7 = 0
A vertex of a square is at the origin and its one side lies along the line 3x – 4y – 10 = 0. Find the area of the square.
Find all the points on the line x + y = 4 that lie at a unit distance from the line 4x+3y=10.
What are the points on the x-axis whose perpendicular distance from the line is 4 units?
The points A(2, 3), B(4, -1) and C(-1, 2) are the vertices of ΔABC. Find the length of the perpendicular from C on AB and hence find the area of ΔABC
Show that the length of the perpendicular from the point (7, 0) to the line 5x + 12y – 9 = 0 is double the length of perpendicular to it from the point (2, 1)
Find the values of k for which the length of the perpendicular from the point (4, 1) on the line 3x – 4y + k = 0 is 2 units
Prove that the product of the lengths of perpendiculars drawn from the points
Find the length of the perpendicular from the origin to each of the following lines : (i) 7x + 24y = 50 (ii) 4x + 3y = 9 (iii) x = 4
Find the distance of the point (4, 2) from the line joining the points (4, 1) and (2, 3)
Find the distance of the point (2, 3) from the line y = 4.
Find the distance of the point (-4, 3) from the line 4(x + 5) = 3(y – 6).
Find the distance of the point (-2, 3) from the line 12x = 5y + 13.
Find the distance of the point (3, -5) from the line 3x – 4y = 27
Reduce each of the following equations to normal form :
Reduce the equation to the normal form x cos ???? + y sin ???? = p, and hence find the values of ???? and p.
Reduce the equation to the normal form x cos ???? + y sin ???? = p, and hence find the values of ???? and p.
Reduce the equation x + y – √2 = 0 to the normal form x cos ???? + y sin ???? = p, and hence find the values of ???? and p.
Find the inclination of the line:
Reduce the equation 5x – 12y = 60 to intercepts form. Hence, find the length of the portion of the line intercepted between the axes
Reduce the equation 3x – 4y + 12 = 0 to intercepts form. Hence, find the length of the portion of the line intercepted between the axes
Reduce the equation y + 5 = 0 to slope-intercept form, and hence find the slope and the y-intercept of the line.
Reduce the equation 5x + 7y – 35 = 0 to slope-intercept form, and hence find the slope and the y-intercept of the line
Reduce the equation 2x – 3y – 5 = 0 to slope-intercept form, and find from it the slope and y-intercept.
Find the equation of the line which is at a distance of 3 units from the origin such that tan ???? = ???? ,where ???? is the acute angle which this perpendicular makes ???????? with t
The length of the perpendicular segment from the origin to a line is 2 units and the inclination of this perpendicular is ???? such that sin ???? = ????/ ???? and ???? is acute.
Find the equation of the line for which p = 4 and ???? = 1800
Answer : Given: p = 4 and ???? = 1800 Here p is the perpendicular that makes an angle ???? with positive direction of x-axis , hence the equation of the straight line is given by: Formula used: x...
Find the equation of the line for which p = 2 and ???? = 3000
Answer : Given: p = 2 and ???? = 3000 Here p is the perpendicular that makes an angle ???? with positive direction of x-axis , hence the equation of the straight line is given by: Formula used: X...
Find the equation of the line for which p = 3 and ???? = 2250
Answer : Given: p = 3 and ???? = 2250 Here p is the perpendicular that makes an angle ???? with positive direction of x-axis , hence the equation of the straight line is given by: Formula used: x...
Find the equation of the line for which p = 8 and ???? = 1500
Answer : Given: p = 8 and ???? = 1500 Here p is the perpendicular that makes an angle ???? with positive direction of x-axis , hence the equation of the straight line is given by: Formula used: x...
Find the equation of the line for which p = 5 and ???? = 1350
Answer : Given: p = 5 and ???? = 1350 Here p is the perpendicular that makes an angle ???? with positive direction of x-axis , hence the equation of the straight line is given by: Formula used: x...
Find the equation of the line for which p = 3 and ???? = 450
Answer : To Find:The equation of the line. Given: p = 3 and ???? = 450 Here p is the perpendicular that makes an angle ???? with positive direction of x-axis , hence the equation of the straight...
If the straight line ????/a + ???? /????=1 find the values of a and b.
A straight line passes through the point (5, -2) and the portion of the line intercepted between the axes is divided at this point in the ratio 2 : 3. Find the equation of the line.
Find the equation of the line whose portion intercepted between the coordinate axes is divided at the point (5, 6) in the ratio 3 : 1.
Find the equation of the line whose portion intercepted between the axes is bisected at the point (3, -2).
Find the equation of the line which passes through the point (22, -6) and whose intercept on the x-axis exceeds the intercept on the y-axis by 5.
Find the equation of the line passing through the point (2, 2) and cutting off intercepts on the axes, whose sum is 9.
Find the equation of the line which passes through the point (3, -5) and cuts off intercepts on the axes which are equal in magnitude but opposite in sign.
Answer : To Find: The equation of the line passing through (3, -5) and cuts off intercepts on the axes which are equal in magnitude but opposite in sign. Given : Let a and b be two intercepts of...
Find the equation of the line and cuts off equal intercepts on the coordinate axes and passes through the point (4,7).
Answer : To Find: The equation of the line with equal intercepts on the coordinate axes and that passes through the point (4,7). Given : Let a and b be two intercepts of x-axis and y-axis...
Find the equation of the line which cuts off intercepts 4 and -6 on the x-axis and y-axis respectively.
Answer : To Find:The equation of the line with intercepts 4 and -6 on the x-axis and y- axis respectively. Given : Let a and b be the intercepts on x-axis and y-axis respectively. Then,x-intercept...
Find the equation of the line which cuts off intercepts -3 and 5 on the x-axis and y-axis respectively.
Answer : To Find: The equation of a line with intercepts -3 and 5 on the x-axis and y- axis respectively. Given :Let a and b be the intercepts on x-axis and y-axis respectively. Then, the...
A line perpendicular to the line segment joining the points (1, 0) and (2, 3) divides it in the ratio 1 : 2. Find the equation of the line.
Find the equation of the line passing through ( – 3, 5) and perpendicular to the line through the points (2, 5) and ( – 3, 6).
Find the equation of the line whose y – intercept is – 3 and which is perpendicular to the line joining the points ( – 2, 3) and (4, – 5).
Find the equation of the line which is perpendicular to the line 3x + 2y = 8 and passes through the midpoint of the line joining the points (6, 4) and (4, – 2).
Find the equation of the line that has x – intercept – 3 and which is perpendicular to the line 3x + 5y = 4
Find the equation of the line passing through the point (2, 4) and perpendicular to the x – axis.
Find the equation of the line passing through the point (2, 3) and perpendicular to the line 4x + 3y = 10
Find the equation of the line passing through the point (0, 3) and perpendicular to the line x – 2y + 5 = 0
Find the equation of the line which is parallel to the line 2x – 3y = 8 and whose y – intercept is 5 units.
Find the equation of the line through the point ( – 1, 5) and making an intercept of – 2 on the y – axis.
Find the equation of the bisectors of the angles between the coordinate axes
Find the equation of the line cutting off an intercept – 2 from the y – axis and equally inclined to the axes.
Find the equation of the line whose inclination is ???????? and which makes an ???? interc
Find the equation of the line which makes an angle of 300 with the positive direction of the x – axis and cuts off an intercept of 4 units with the negative direction of the y – axis.
If A(1, 4), B(2, – 3) and C( – 1, – 2) are the vertices of a ΔABC, find the equation of (i) the median through A (ii) the altitude through A (iii) the perpendicular bisector of BC
the midpoints of the sides BC, CA and AB of a ΔABC are D(2, 1), B( – 5, 7) and P( – 5, – 5) respectively. Find the equations of the sides of ΔABC.
If A(4, 3), B(0, 0) and C(2, 3) are the vertices of a ΔABC, find the equation of the bisector of ∠A.
. Find the equations of the altitudes of a ΔABC, whose vertices are A(2, – 2), B(1, 1) and C( – 1, 0).
Find the slope and the equation of the line passing through the points: ( – 1, 1) and (2, – 4)
Find the equation of a line whose inclination with the x – axis is 1500 and which passes through the point (3, – 5).
Find the equation of a line which is equidistant from the lines y = 8 and y = – 2.
. Using slopes, find the value of x for which the points A(5, 1), B(1, -1) and C(x, 4) are collinear.
Without using Pythagora’s theorem, show that the points A(1, 2), B(4, 5) and C(6, 3) are the vertices of a right-angled triangle.
Find the distance between the points:
(i) A(2, -3) and B(-6, 3)
(ii) C(-1, -1) and D(8, 11)
(iii) P(-8, -3) and Q(-2, -5)
(iv) R(a + b, a – b) and S(a – b, a + b)
Mark (√) against the correct answer in the following: The range of 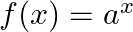 , where
, where 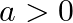 is
is
A. ![Rendered by QuickLaTeX.com [-\infty, 0]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-94a61bc9af7b9f196d46b44726815c11_l3.png)
B. 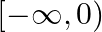
C. 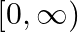
D. 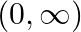
Solution: Option(D) is correct. $f(x)=a x$, where $a>0$ Case 1 : When $x<0$, then ax lies between $(0,1)$ Case 2 : When $x \geq 0$, then $a x \geq 1$ Union of above two cases, gives us the...
Mark (√) against the correct answer in the following: Let 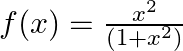 . Then, range
. Then, range 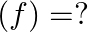
A. 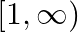
B. 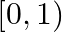
C. ![Rendered by QuickLaTeX.com [-1,1]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-bd9ec9b7fdf72f6f954becf26cf7129a_l3.png)
D. ![Rendered by QuickLaTeX.com (0,1]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3243e3012721250a044fef79f51a0c2f_l3.png)
Solution: Option (B) is correct. $\mathrm{f}(\mathrm{x})=\frac{x^{2}}{\left(1+x^{2}\right)}$ The range of $f(x)$ can be found out by putting $f(x)=y$ $\begin{array}{l}...
Mark (√) against the correct answer in the following: Let 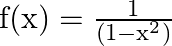 . Then, range
. Then, range 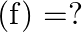
A. ![Rendered by QuickLaTeX.com (-\infty, 1]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2eb654b4016c2cc85fa136277a9d7f78_l3.png)
B. 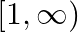
C. ![Rendered by QuickLaTeX.com [-1,1]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-bd9ec9b7fdf72f6f954becf26cf7129a_l3.png)
D. none of these
Solution: Option(B) is correct. $f(x)=\frac{1}{\left(1-x^{2}\right)}$ The range of $f(x)$ can be found out by putting $f(x)=y$ $\begin{array}{l} \mathrm{y}=\frac{1}{\left(1-x^{2}\right)} \\...
Mark (√) against the correct answer in the following: Let 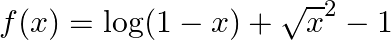 . Then,
. Then, 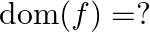
A. 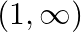
B. ![Rendered by QuickLaTeX.com (-\infty,-1]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-17e48fe12e81cf52057d1a1ecdfc8269_l3.png)
C. 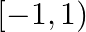
D. 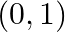
Solution: Option (B) is correct. $f(x)=\log (1-x)+\sqrt{x^{2}-1}$ Solving inequality, $\log (1-x) \geq 0$ $\Rightarrow 1-x \geq \mathrm{e}^{0} \quad \begin{array}{c}\text { (Log taken to the...
Mark (√) against the correct answer in the following: Let 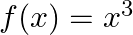 . Then, dom (f) and range (f) are respectively
. Then, dom (f) and range (f) are respectively
A. 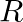 and
and 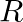
B. 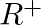 and
and 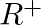
C. R and R +
D. 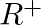 and
and 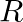
Solution: Option(A) is correct. $f(x)=x^{3}$ $f(x)$ can assume any value, therefore domain of $f(x)$ is $R$ Range of the function can be positive or negative Real numbers, as the cube of any number...
Mark (√) against the correct answer in the following: Let 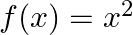 . Then, dom (f) and range (f) are respectively.
. Then, dom (f) and range (f) are respectively.
A. 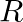 and
and 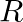
B. 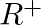 and
and 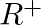
C. 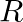 and
and 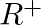
D. 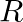 and
and 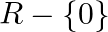
Solution: Option(C) is correct. $f(x)=x_{2}$ $f(x)$ can assume any value, therefore domain of $f(x)$ is $R$ Range of the function can only be positive Real numbers, as the square of any number is...
Mark (√) against the correct answer in the following: Let 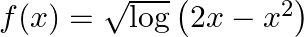 . Then,
. Then, 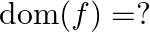
A. 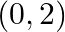
B. ![Rendered by QuickLaTeX.com [1,2]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-ab425e31cf7af5fb3d46646ff538fdcd_l3.png)
C. ![Rendered by QuickLaTeX.com (-\infty, 1]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2eb654b4016c2cc85fa136277a9d7f78_l3.png)
D. None of these
Solution: Option(C) is correct. $f(x)=\sqrt{\log \left(2 x-x^{2}\right)}$ For $f(x)$ to be defined $2 x-x^2$ should be positive. Solving inequality, (Log taken to the opposite side of the equation...
Mark (√) against the correct answer in the following: Let 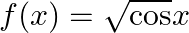 . Then,
. Then, 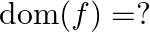
A. ![Rendered by QuickLaTeX.com \left[0, \frac{\pi}{2}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-cdf7f72b896a3c8ef3745557ca17a3c9_l3.png)
B. ![Rendered by QuickLaTeX.com \left[\frac{3 \pi}{2}, 2 \pi\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-aa7b802c7af63a3c3f09db8b0292cb35_l3.png)
C. ![Rendered by QuickLaTeX.com \left[0, \frac{\pi}{2}\right] \cup\left[\frac{3 \pi}{2}, 2 \pi\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-be8b8bc855076ca9e77d0af23204c861_l3.png)
D. none of these
Solution: Option(C) is correct. $\mathrm{f}(\mathrm{x})=\sqrt{\cos x}$ As per graph of $\sqrt{\cos x}$ the domain is $\left[0, \frac{\pi}{2}\right] \cup\left[\frac{3 \pi}{2}, 2 \pi\right]$
Mark (√) against the correct answer in the following: Let 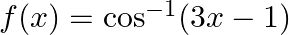 . Then,
. Then, 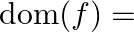 ?
?
A. 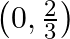
B. ![Rendered by QuickLaTeX.com \left[0, \frac{2}{3}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b52292076dc04c74fe44cded15544d8b_l3.png)
C. ![Rendered by QuickLaTeX.com \left[\frac{-2}{3}, \frac{2}{3}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c6d1d6173855bcc8e2e22c311f052282_l3.png)
D. None of these
Solution: Option(B) is correct. $\begin{array}{l} \mathrm{f}(\mathrm{x})=\cos ^{-1}(3 \mathrm{x}-1) \end{array}$ Domain for function $\cos ^{-1} \mathrm{x}$ is $[-1,1]$ and range is $[0, \pi]$ When...
Mark (√) against the correct answer in the following: Let 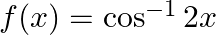 . Then,
. Then, 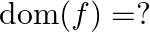
A. ![Rendered by QuickLaTeX.com [-1,1]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-bd9ec9b7fdf72f6f954becf26cf7129a_l3.png)
B. ![Rendered by QuickLaTeX.com \left[\frac{-1}{2}, \frac{1}{2}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2b2127e7c856ce7280a6fc7257d27da7_l3.png)
C. ![Rendered by QuickLaTeX.com \left[\frac{-\pi}{2}, \frac{\pi}{2}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d03f7933dddf8dbceee8c92c85707a25_l3.png)
D. ![Rendered by QuickLaTeX.com \left[\frac{-\pi}{4}, \frac{\pi}{4}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-36caf65bb0d2f985fd702c950c7c7653_l3.png)
Solution: Option(B) is correct. $f(x)=\cos ^{-1}2 x$ Domain for function $\cos ^1 \mathrm{x}$ is $[-1,1]$ and range is $[0, \pi]$ When a function is multiplied by an integer, the domain of the...
Mark (√) against the correct answer in the following: Let 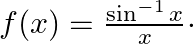 Then,
Then, 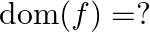
A. 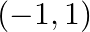
B. ![Rendered by QuickLaTeX.com [-1,1]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-bd9ec9b7fdf72f6f954becf26cf7129a_l3.png)
C. ![Rendered by QuickLaTeX.com [-1,1]-\{0\}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-0d140ee7fc9eafbc15a3b47a6ad32f55_l3.png)
D. none of these
Solution: Option(B) is correct. $f(x)=\frac{\sin ^{-1} x}{x}$ The domain of the function is defined for $\mathrm{x} \neq 0$ domain of $\sin ^{-1} x$ is $[-1,1]$ So, domain of...
Mark (√) against the correct answer in the following: Let 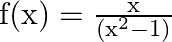 . Then,
. Then, 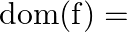 ?
?
A. 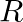
B. 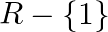
C. 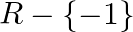
D. 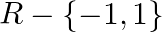
Solution: Option(D) is correct. $\mathrm{f}(\mathrm{x})=\frac{x}{\left(x^{2}-1\right)}$ The domain of the function is defined for $\begin{array}{l} \mathrm{x}^{2}-1 \neq 0 \\ \Rightarrow \mathrm{x}...
Mark (√) against the correct answer in the following: Let 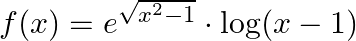 . Then,
. Then, 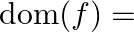 ?
?
A. ![Rendered by QuickLaTeX.com (-\infty, 1]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2eb654b4016c2cc85fa136277a9d7f78_l3.png)
B. 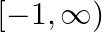
C. 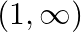
D. ![Rendered by QuickLaTeX.com (-\infty,-1] \cup(1, \infty)](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f70651ff938d8644c2a7b1e4ab8dcdbc_l3.png)
Solution: Option(C) is correct. $\mathrm{f}(\mathrm{x})=e^{\sqrt{x^{2}-1}} \cdot \log (x-1)$ The domain of the function is defined for $\begin{array}{l} \mathrm{x}-1>0 \quad \text { and }...
Mark (√) against the correct answer in the following: Let 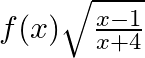 . Then, dom (f) – ?
. Then, dom (f) – ?
A. 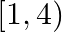
B. ![Rendered by QuickLaTeX.com [1,4]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b466cd4c540c856fc9d44d24b88d173d_l3.png)
C. ![Rendered by QuickLaTeX.com (-\infty, 4]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7342c3266939896b38339bca55408448_l3.png)
D. ![Rendered by QuickLaTeX.com (-\infty, 1] \cup(4, \infty)](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3cacb249d82a72cc2e90b22ea1598fb5_l3.png)
Solution: Option(D) is correct. $\mathrm{f}(\mathrm{x})=\sqrt{\frac{x-1}{x+4}}$ The domain of the function can be defined for $\sqrt{\frac{x-1}{x+4}} \geq 0$ $\begin{array}{l} \Rightarrow...
Mark (√) against the correct answer in the following: Let 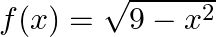 . Then, dom
. Then, dom 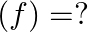
A. ![Rendered by QuickLaTeX.com [-3,3]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-9cbb1b08c8e67cf43d5548e7d359de56_l3.png)
B. ![Rendered by QuickLaTeX.com [-\infty,-3]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-697587bce5e8d6c46d3797bdabaae044_l3.png)
C. 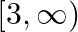
D. ![Rendered by QuickLaTeX.com (-\infty,-3] \cup(4, \infty)](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b4747a453581bf4e2adb77e958e00ac9_l3.png)
Solution: Option(A) is correct. $\mathrm{f}(\mathrm{x})=\sqrt{9-x^{2}}$ The domain of the function can be defined for $\sqrt{9-x^{2}} \geq 0$ $\begin{array}{l} \Rightarrow \sqrt{9-x^{2}} \geq 0 \\...
Mark (√) against the correct answer in the following: If f = {(1, 2), (3, 5), (4, 1)} and g = {(2, 3), (5, 1), (1, 3)} then (g o f) = ?
A. {(3, 1), (1, 3), (3, 4)}
B. {(1, 3), (3, 1), (4, 3)}
C. {(3, 4), (4, 3), (1, 3)}
D. {(2, 5), (5, 2), (1, 5)}
Solution: Option(B) is correct. $\begin{array}{l} \mathrm{f}=\{(1,2),(3,5),(4,1)\} \\ \mathrm{g}=\{(2,3),(5,1),(1,3)\} \end{array}$ According to the combination of $\mathrm{f}$ and $\mathrm{g}$,...
Mark (√) against the correct answer in the following: If 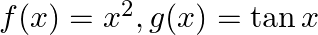 and
and 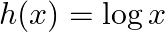 then
then 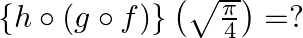
A. 0
B. 1
C. 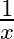
D. 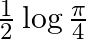
Solution: Option(A) is correct. $\begin{array}{l} f(x)=x ^2 \\ g(x)=\tan x \\ h(x)=\log x \end{array}$ According to the combination of $f, g$ and $h$,...
Mark (√) against the correct answer in the following: If 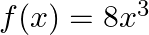 and
and  then
then 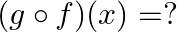
A. 
B. 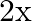
C. 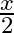
D. 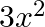
Solution: Option(B) is correct. $f(x)=8 x^{3}$ $g(x)=x^{1 / 3}$ According to the combination of $\mathrm{f}$ and $\mathrm{g}$, $\operatorname{gof}(\mathrm{x})=\mathrm{f}(\mathrm{f}(\mathrm{x}))$...
Mark (√) against the correct answer in the following: If 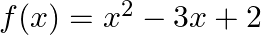 then
then 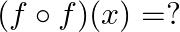
A. 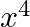
B. 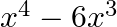
C. 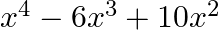
D. None of these
Solution: Option(D) is correct. $f(x)=x^2-3 x+2$ According to the combination of $\mathrm{f}$ and $\mathrm{f}$, $\operatorname{fof}(x)=f(f(x))$ Therefore, fof $(x)=f(f(x))$ $\begin{array}{l}...
Mark (√) against the correct answer in the following: If ![Rendered by QuickLaTeX.com f(x)=\sqrt[3]{3-x^{3}}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-6c33645c75bd40d87b10258556b03f43_l3.png) then (f of)
then (f of) 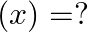
A. 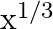
B. 
C. 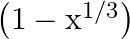
D. None of these
Solution: Option(B) is correct. $f(x) \sqrt[3]{3-x^{3}}$ According to the combination of $f$ and $f$, $\text { fof }(x)=f(f(x))$ Therefore, fof $(x)=f(f(x))$...
Mark (√) against the correct answer in the following: If 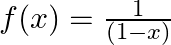 then (f of of)
then (f of of) 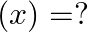
A. 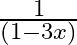
B. 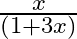
C. 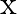
D. None of these
Solution: Option(C) is correct. $\mathrm{f}(\mathrm{x})=\frac{1}{(1-x)}$ According to the combination of $\mathrm{f}$ and $\mathrm{f}$, fofof $(x)=f(f(f(x)))$ Therefore, fof $(x)=f(f(f(x))$...
Mark (√) against the correct answer in the following: If 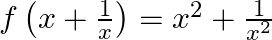 then
then 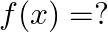
A. 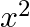
B. 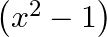
C. 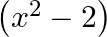
D. None of these
Solution: Option(C) is correct. $\begin{array}{l} \mathrm{f}\left(\mathrm{x}+\frac{1}{x}\right)=\left(\mathrm{x} ^2+\frac{1}{x^{2}}\right) \\ \Rightarrow...
Mark (√) against the correct answer in the following: If 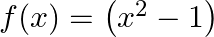 and
and 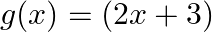 then
then 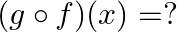
A. 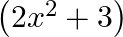
B. 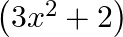
C. 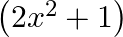
D. None of these
Solution: Option(C) is correct. $\begin{array}{l} \mathrm{f}(\mathrm{x})=(\mathrm{x}^2-1) \\ \mathrm{g}(\mathrm{x})=(2 \mathrm{x}+3) \end{array}$ According to the combination of $\mathrm{f}$ and...
Mark (√) against the correct answer in the following: If 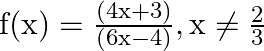 then
then 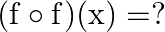
A. 
B. 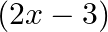
C. 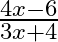
D. None of these
Solution: Option(A) is correct. $\mathrm{f}(\mathrm{x})=\frac{(4 x+3)}{(6 x-4)}, \mathrm{x} \neq \frac{2}{3}$ According to the combination of $\mathrm{f}$ and $\mathrm{f}$,...
Mark (√) against the correct answer in the following: Let f : N → X : f(x) = 4×2 + 12x + 15. Then, 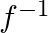 (y) = ?
(y) = ?
A. 
B. 
C. 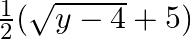
D. None of these
Solution: Option(B) is correct. $\mathrm{f}: \mathrm{N} \rightarrow \mathrm{X}: \mathrm{f}(\mathrm{x})=4 \mathrm{x} 2+12 \mathrm{x}+15$ We need to find $\mathrm{f}-1$, Suppose...
Mark (√) against the correct answer in the following:
Let 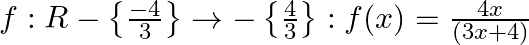 . Then
. Then 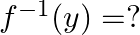
A. 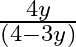
B. 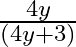
C. 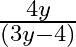
D. None of these
Solution: Option(A) is correct. $\text { f: } R-\left\{-\frac{4}{3}\right\} \rightarrow-\left\{\frac{4}{3}\right\}: f(x)=\frac{4 x}{(3 x+4)}$ We need to find $\mathrm{f}-1$ Suppose $f(x)=y$...
Mark (√) against the correct answer in the following: Let f : Q → Q : f(x) = (2x + 3). Then, 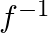 (y) = ?
(y) = ?
A. (2y – 3)
B. 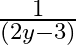
C. 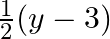
D. none of these
Solution: Option(C) is correct. $\mathrm{f}: \mathrm{Q} \rightarrow \mathrm{Q}: \mathrm{f}(\mathrm{x})=(2 \mathrm{x}+3)$ We need to find $\mathrm{f}-1$ Suppose $\mathrm{f}(\mathrm{x})=\mathrm{y}$...
Mark (√) against the correct answer in the following:
Let A and B be two non – empty sets and let
f : (A × B) → (B × A) : f(a, b) = (b, a). Then, f is
A. one – one and into
B. one – one and onto
C. many – one and into
D. many – one and onto
Solution: Option(B) is correct. One-One Function Suppose $\mathrm{p}_{1}, \mathrm{p}_{2}, \mathrm{q}_{1}, \mathrm{q}_{2}$ be two arbitrary elements in $\mathrm{R}$ + Therefore, $f\left(p_{1},...
Mark (√) against the correct answer in the following: Let 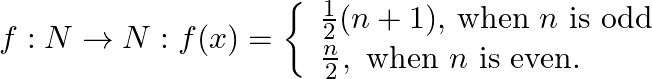 Then,
Then, 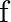 is
is
A. one – one and into
B. one – one and onto
C. many – one and into
D. many – one and onto
Solution: Option(D) is correct. $f:\mathrm{N} \rightarrow \mathrm{N}: \mathrm{f}(\mathrm{x})=$ $f: N \rightarrow N: f(x)=\left\{\begin{array}{l}\frac{1}{2}(n+1) \text {, when } n \text { is odd } \\...
Mark (√) against the correct answer in the following:
Let 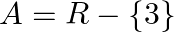 and
and 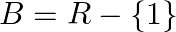 . Then
. Then 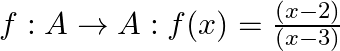 is
is
A. one – one and into
B. one – one and onto
C. many – one and into
D. many – one and onto
Solution: Option(B) is correct. f: $\mathrm{A} \rightarrow \mathrm{B}: \mathrm{f}(\mathrm{x})=\frac{(x-2)}{(x-3)}$ Where, $\mathrm{A}=\mathrm{R}-\{3\}$ and $\mathrm{B}=\mathrm{R}-\{1\}$ One-One...
Mark (√) against the correct answer in the following:
f : C → R : f(z) = |z| is
A. one – one and into
B. one – one and onto
C. many – one and into
D. many – one and onto
Solution: Option() is correct. One-One function Suppose $\mathrm{p}, \mathrm{q}$ be two arbitrary elements in $\mathrm{R}+$ Therefore, $f(p)=f(q)$ $\begin{array}{l}...
Mark (√) against the correct answer in the following:
f : R → R : f(x) = cos x is
A. one – one and into
B. one – one and onto
C. many – one and into
D. many – one and onto
Solution: Option (C) is correct. One-one function $\cos x$ graph cuts y axis repeatedly, hence it is many-one. Onto function Range of $f(x)$ is $[-1,1]$ Co-domain is $\mathrm{R}$ So here, Range of...
Mark (√) against the correct answer in the following:
f : R + → R + : f(x) = 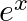 is
is
A. many – one and into
B. many – one and onto
C. one – one and into
D. one – one and onto
Solution: Option(D) is correct. One-One function Suppose $\mathrm{p}, \mathrm{q}$ be two arbitrary elements in $\mathrm{R}+$ Therefore, $f(p)=f(q)$ $\begin{array}{l} \Rightarrow...
Mark (√) against the correct answer in the following:
f : R → R : f(x) =  is
is
A. one – one and onto
B. one – one and into
C. many – one and onto
D. many – one and into
Solution: Option(B) is correct. One-One function Suppose $\mathrm{p}, \mathrm{q}$ be two arbitrary elements in $\mathrm{R}$ Therefore, $f(p)=f(q)$ $\begin{array}{l} \Rightarrow...
Mark (√) against the correct answer in the following:
f : R → R : f(x) = 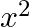 is
is
A. one – one and onto
B. one – one and into
C. many – one and onto
D. many – one and into
Solution: Option(D) is correct. One-One function Suppose $\mathrm{p}, \mathrm{q}$ be two arbitrary elements in $\mathrm{R}$ Therefore, $f(p)=f(q)$ $\begin{array}{l} \Rightarrow...
Mark (√) against the correct answer in the following:
f : N → N : f(x) = 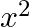 + x + 1 is
+ x + 1 is
A. one – one and onto
B. one – one and into
C. many – one and onto
D. many – one and into
Solution: Option (B) is correct. One-One function Suppose $\mathrm{p}, \mathrm{q}$ be two arbitrary elements in $\mathrm{N}$ Therefore, $f(p)=f(q)$ $\begin{array}{l} \Rightarrow...
Mark (√) against the correct answer in the following:
f : N → N : f(x) = 2x is
A. one – one and onto
B. one – one and into
C. many – one and onto
D. many – one and into
Solution: Option (B) is correct. One-One function Suppose $\mathrm{p}, \mathrm{q}$ be two arbitrary elements in $\mathrm{N}$ Therefore, $f(p)=f(q)$ $\begin{array}{l} \Rightarrow 2 \mathrm{p}=2...
Temperature dependence of resistivity ρ(T) of semiconductors, insulators, and metals is significantly based on the following factors:
a) number of charge carriers can change with temperature T
b) time interval between two successive collisions can depend on T
c) length of material can be a function of T
d) mass of carriers is a function of T
The correct answer is a) number of charge carriers can change with temperature T b) time interval between two successive collisions can depend on T
Let g = {(1, 2), (2, 5), (3, 8), (4, 10), (5, 12), (6, 12)}. Is g a function? If yes, its domain range. If no, give reason.
Answer : Given: g = {(1, 2), (2, 5), (3, 8), (4, 10), (5, 12), (6, 12)} We know that, A function ‘f’ from set A to set B is a correspondence (rule) which associates elements of set A to elements of...
Define a function. What do you mean by the domain and range of a function? Give examples.
Solution: A function is stated as the relation between the two sets, where there is exactly one element in set B, for every element of set A. A function is represented as f: A → B, which means ‘f’...
Let A = {1, 2, 3} and R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3)}. Show that R is reflexive but neither symmetric nor transitive.
Solution: $A=\{1,2,3\}$ and $\bar{R}=\{(1,1),(2,2),(3,3),(1,2),(2,3)\}$ (Given) $\mathrm{R}$ is reflexive if $\mathrm{a} \in \mathrm{A}$ and $(\mathrm{a}, \mathrm{a}) \in \mathrm{R}$ Here,...
Let 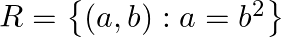 for all
for all 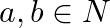 Show that R satisfies none of reflexivity, symmetry and transitivity.
Show that R satisfies none of reflexivity, symmetry and transitivity.
Solution: $\mathrm{R}=\left\{(\mathrm{a}, \mathrm{b}): \mathrm{a}=\mathrm{b}_{2}\right\}$ for all $\mathrm{a}, \mathrm{b} \in \mathrm{N}$ (As given) Non-Reflexivity: Assume $a$ be an arbitrary...
Let S be the set of all points in a plane and let R be a relation in S defined by R = {(A, B) : d(A, B) < 2 units}, where d(A, B) is the distance between the points A and B. Show that R is reflexive and symmetric but not transitive.
Solution: $\mathrm{R}=\{(\mathrm{A}, \mathrm{B}): \mathrm{d}(\mathrm{A}, \mathrm{B})<2$ units $\}$, where $\mathrm{d}(\mathrm{A}, \mathrm{B})$ is the distance between the points $\mathrm{A}$ and...
Let 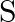 be the set of all real numbers and let
be the set of all real numbers and let 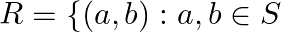 and
and 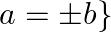 Show that
Show that 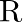 is an equivalence relation on
is an equivalence relation on 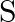 .
.
Solution: $\mathrm{R}=\{(\mathrm{a}, \mathrm{b}): \mathrm{a}, \mathrm{b} \in \mathrm{S}$ and $\mathrm{a}=\pm \mathrm{b}\} .$ (Given) If $\mathrm{R}$ is Reflexive, Symmetric and Transitive, then...
Show that the relation 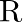 on
on  , defined by
, defined by 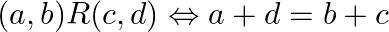 is an equivalent relation.
is an equivalent relation.
Solution: If $R$ is Reflexive, Symmetric and Transitive, then $R$ is an equivalence relation. Reflexivity: Suppose $a$ and $\mathrm{b}$ be an arbitrary element of $\mathrm{N} \times \mathrm{N}$...
Let 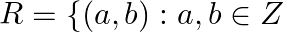 and
and 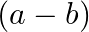 is divisible by 5
is divisible by 5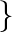 Show that
Show that 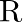 is an equivalence relation on
is an equivalence relation on 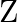 .
.
Solution: $\mathrm{R}=\{(\mathrm{a}, \mathrm{b}): \mathrm{a}, \mathrm{b} \in \mathrm{Z}$ and $(\mathrm{a}-\mathrm{b})$ is divisible by 5$\}$ (As given) If $R$ is Reflexive, Symmetric and Transitive,...
Let  be the set of all triangles in a plane. Show that the relation
be the set of all triangles in a plane. Show that the relation 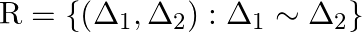 is an equivalence relation on
is an equivalence relation on 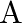 .
.
Solution: Suppose $\mathrm{R}=\left\{\left(\Delta 1, \Delta_{2}\right): \Delta_{1} \sim \Delta_{2}\right\}$ be a relation defined on A. (As given) If $\mathrm{R}$ is Reflexive, Symmetric and...
Define a relation on a set. What do you mean by the domain and range of a relation? Give an example.
Solution: Relation: Suppose $P$ and $Q$ are two sets. Therefore, a relation $R$ from $P$ to $Q$ is a subset of $P \times Q$. Therefore, $\mathrm{R}$ is a relation to $\mathrm{P}$ to $\mathrm{Q}...
Let A = {1, 2, 3, 4, 5, 6) and let R = {(a, b) : a, b ∈ A and b = a + 1}. Show that R is
(i) not reflexive,
(ii) not symmetric
Solution: A $= (1, 2, 3, 4, 5, 6)$ and $R = {(a, b): a, b \in \text{A and b} = a + 1}$ (As given) Therefore, R = {(1,2), (2,3), (3,4), (4,5), (5,6)} (i) Non−reflexive: If $x \in A$ and $(x, x) \in...
