Solution: (i) One-One but not Onto $\mathrm{f}: \mathrm{N} \rightarrow \mathrm{N}$ be a mapping given by $\mathrm{f}(\mathrm{x})=\mathrm{x} 2$ For one-one $\begin{array}{l} f(x)=f(y) \\ x_{2}=y z \\...
Solution: (i) Into Function: It is is a function where there is atleast one element is Set B who is not the image of any element in set A. For Example: $f(x) = 2x - 1$ from the set of Integers to...
Solution: (i)Bijective function: It is, also known as one-one onto function and is a function where for every element of set A, there is exactly one image in set B, such that no element is set B is...
Solution: (i) Injective function: It is, also known as one-one function and is a type of function where every element in set A has an image in set B. Hence, f: A → B is one-one or injection function...
Solution: A function is stated as the relation between the two sets, where there is exactly one element in set B, for every element of set A. A function is represented as f: A → B, which means ‘f’...
(iii) Given: B = {1, 3} and C = {3, 5} To find: B × C By the definition of the Cartesian product, Given two non – empty sets P and Q. The Cartesian product P × Q is the set of all ordered pairs of...
Answer : (i) Given: A = {-3, -1} and B = {1, 3} To find: A × B By the definition of the Cartesian product, Given two non – empty sets P and Q. The Cartesian product P × Q is the set of all ordered...
Answer : We have, A = {5, 7} So, By the definition of the Cartesian product, Given two non – empty sets P and Q. The Cartesian product P × Q is the set of all ordered pairs of elements from P and Q,...
(iii) Given: A = {-2, 2} To find: A × A By the definition of the Cartesian product, Given two non – empty sets P and Q. The Cartesian product P × Q is the set of all ordered pairs of elements from P...
Answer : (i) Given: A = {-2, 2} and B = {0, 3, 5} To find: A × B By the definition of the Cartesian product, Given two non – empty sets P and Q. The Cartesian product P × Q is the set of all ordered...
Answer : Since, (a, 0), (b, 1), (c, 0) are the elements of A × B. ∴ a, b, c Є A and 0, 1 Є B It is given that n(A) = 3 and n(B) = 2 ∴ a, b, c Є A and n(A) = 3 ⇒ A = {a, b, c} and 0, 1 Є B and n(B) =...
Answer : Given: A × B = {(a, b): b = 3a – 2} and {(x, -5), (2, y)} Є A × B For (x, -5) Є A × B b = 3a – 2 ⇒ -5 = 3(x) – 2 ⇒ -5 + 2 = 3x ⇒ -3 = 3x ⇒ x = -1 For (2, y) Є A × B b = 3a – 2 ⇒ y = 3(2) –...
Answer : Given: A = {2, 3} and B = {4, 5} To find: A × B By the definition of the Cartesian product, Given two non – empty sets P and Q. The Cartesian product P × Q is the set of all ordered pairs...
Answer : Here, A × B = {(–2, 3), (–2, 4), (0, 4), (3, 3), (3, 4)} To find: A and B Clearly, A is the set of all first entries in ordered pairs in A × B ∴ A = {-2, 0, 3} and B is the set of all...
Answer : (i) Given: A = {x ϵ W : x < 2} Here, W denotes the set of whole numbers (non – negative integers). ∴ A = {0, 1} [∵ It is given that x < 2 and the whole numbers which are less than 2...
Answer : (i) Given: A = {1, 3, 5}, B = {3, 4} and C = {2, 3} H. S = A × (B ⋃ C) By the definition of the union of two sets, (B ⋃ C) = {2, 3, 4} = {1, 3, 5} × {2, 3, 4} Now, by the definition of the...
Answer : Given: A = {x ϵ N: x ≤ 3} Here, N denotes the set of natural numbers. ∴ A = {1, 2, 3} [∵ It is given that the value of x is less than 3 and natural numbers which are less than 3 are 1 and...
(iii) Given: A = {2, 3, 5} and B = {2, 3, 5} To find: A × A By the definition of the Cartesian product, Given two non – empty sets P and Q. The Cartesian product P × Q is the set of all ordered...
Answer : (i) Given: A = {2, 3, 5} and B = {5, 7} To find: A × B By the definition of the Cartesian product, Given two non – empty sets P and Q. The Cartesian product P × Q is the set of all ordered...
Answer : Given: P = {a, b} and Q = {x, y, z} To show: P × Q ≠ Q × P Now, firstly we find the P × Q and Q × P By the definition of the Cartesian product, Given two non – empty sets P and Q. The...
Answer : Given: A = {9, 1} and B = {1, 2, 3} To show: A × B ≠ B × A Now, firstly we find the A × B and B × A By the definition of the Cartesian product, Given two non – empty sets P and Q. The...
Since, the ordered pairs are equal, the corresponding elements are ∴, a – 2 = b – 1 …(i) & 2b + 1 = a + 2 …(ii) Solving eq. (i), we get a – 2 = b – 1 ⇒ a – b = -1 + 2 ⇒ a – b = 1 … (iii) Solving...
Answer : Since, the ordered pairs are equal, the corresponding elements are equal. ∴, a + 3 = 5 …(i) and b – 2 = 1 …(ii) Solving eq. (i), we get a + 3 = 5 ⇒ a = 5 – 3 ⇒ a = 2 Solving eq. (ii), we...
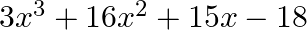is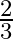 
. Find the other zeros of the polynomial.$x=\frac{2}{3}$ is one of the zero of $3 x^{3}+16 x^{2}+15 x-18$ Now, we have $\mathrm{x}=\frac{2}{3}$ $\Rightarrow \mathrm{x}-\frac{2}{3}=0$ Now, we divide $3 x^{3}+16 x^{2}+15 x-18$ by...
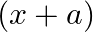is a factor of the polynomial 
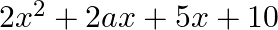, find the value of 
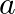.$(x+a)$ is a factor of $2 x^{2}+2 a x+5 x+10$ $x+a=0$ $\Rightarrow \mathrm{x}=-\mathrm{a}$ Since, it satisfies the above polynomial. => $2(-a)^{2}+2 a(-a)+5(-a)+10=0$ $\Rightarrow 2 a^{2}-2...
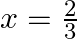and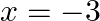 
are the roots of the quadratic equation 
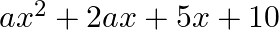then find the value of a and 
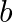.$a x^{2}+7 x+b=0$ Since, $x=\frac{2}{3}$ is the root of the above quadratic equation Hence, it will satisfy the above equation. => $a\left(\frac{2}{3}\right)^{2}+7\left(\frac{2}{3}\right)+b=0$...
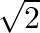and their product is 
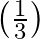.Quadratic equation can be found if we know the sum of the roots and product of the roots by using the formula: $\mathrm{x}^{2}-($ Sum of the roots) $\mathrm{x}+$ Product of roots $=0$ $\Rightarrow...
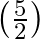and their product is 1 . Hence, find the zeroes of the polynomial.Let $\alpha$ and $\beta$ be the zeroes of the required polynomial $\mathrm{f}(\mathrm{x})$. =>$(\alpha+\beta)=\frac{5}{2}$ and $\alpha \beta=1$ $\therefore...
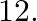Hence, find the zeroes of the polynomial.Let $\alpha$ and $\beta$ be the zeroes of the required polynomial $\mathrm{f}(\mathrm{x})$. Then $(\alpha+\beta)=8$ and $\alpha \beta=12$ $\therefore f(x)=x^{2}-(\alpha+\beta) x+\alpha \beta$...
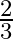and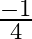 
. Verify the relation between the coefficients and the zeroes of the polynomial.Let $\alpha=\frac{2}{3}$ and $\beta=\frac{-1}{4}$. Sum of the zeroes $=(\alpha+\beta)=\frac{2}{3}+\left(\frac{-1}{4}\right)=\frac{8-3}{12}=\frac{5}{12}$ Product of the zeroes, $\alpha...
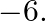Verify the relation between the coefficients and the zeroes of the polynomial.Let $\alpha=2$ and $\beta=-6$ Sum of the zeroes, $(\alpha+\beta)=2+(-6)=-4$ Product of the zeroes, $\alpha \beta=2 \times(-6)=-12$ $\therefore$ Required polynomial $=\mathrm{x}^{2}-(\alpha+\beta)...
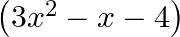and verify the relation between the zeroes and the coefficients.$$ \begin{aligned} &3 x^{2}-x-4=0 \\ &\Rightarrow 3 x^{2}-4 x+3 x-4=0 \\ &\Rightarrow x(3 x-4)+1(3 x-4)=0 \\ &\Rightarrow(3 x-4)(x+1)=0 \\ &\Rightarrow(3 x-4) \text { or }(x+1)=0 \\ &\Rightarrow...
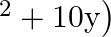and verify the relation between the zeroes and the coefficients.f(u)=5u2+10u \mathrm{f}(\mathrm{u})=5 \mathrm{u}^{2}+10 \mathrm{u} It can be written as $5 \mathrm{u}(\mathrm{u}+2)$ ∴f(u)=0⇒5u=0 or u+2=0 \therefore \mathrm{f}(\mathrm{u})=0...
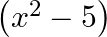and verify the relation between the zeroes and the coefficients.$$ \begin{aligned} &f(x)=x^{2}-5 \\ &\text { It can be written as } x^{2}+0 x-5 . \\ &=\left(x^{2}-(\sqrt{5})^{2}\right) \\ &=(x+\sqrt{5})(x-\sqrt{5}) \\ &\therefore f(x)=0...
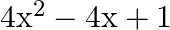and verify the relation between the zeroes and the coefficients.$$ \begin{aligned} &4 x^{2}-4 x+1=0 \\ &\Rightarrow(2 x)^{2}-2(2 x)(1)+(1)^{2}=0 \end{aligned} $$ $$ \begin{aligned} &\Rightarrow(2 \mathrm{x}-1)^{2}=0 \quad\left[\because \mathrm{a}^{2}-2...
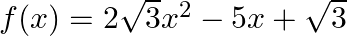and verify the relation between its zeroes and coefficients.$$ \begin{aligned} &2 \sqrt{3} x^{2}-5 x+\sqrt{3} \\ &\Rightarrow 2 \sqrt{3} x^{2}-2 x-3 x+\sqrt{3} \\ &\Rightarrow 2 x(\sqrt{3} x-1)-\sqrt{3}(\sqrt{3} x-1)=0 \\ &\Rightarrow(\sqrt{3} x-1) \text {...
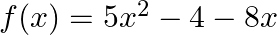and verify the relationship between the zeroes and coefficients of the given polynomial.$f(x)=5 x^{2}-4-8 x$ $=5 x^{2}-8 x-4$ $=5 x^{2}-(10 x-2 x)-4$ $=5 x^{2}-10 x+2 x-4$ $=5 x(x-2)+2(x-2)$ $=(5 x+2)(x-2)$ $\therefore \mathrm{f}(\mathrm{x})=0 \Rightarrow(5...
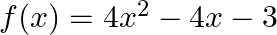and verify the relation between its zeroes and coefficients.$f(x)=4 x^{2}-4 x-3$ $=4 x^{2}-(6 x-2 x)-3$ $=4 x^{2}-6 x+2 x-3$ $=2 x(2 x-3)+1(2 x-3)$ $=(2 x+1)(2 x-3)$ $\therefore \mathrm{f}(\mathrm{x})=0 \Rightarrow(2 \mathrm{x}+1)(2 \mathrm{x}-3)=0$...
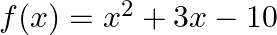and verify the relation between its zeroes and coefficients.$f(x)=x^{2}+3 x-10$ $=x^{2}+5 x-2 x-10$ $=x(x+5)-2(x+5)$ $=(x-2)(x+5)$ $\therefore \mathrm{f}(\mathrm{x})=0 \Rightarrow(\mathrm{x}-2)(\mathrm{x}+5)=0$ $\Rightarrow x-2=0$ or $x+5=0$ $\Rightarrow...
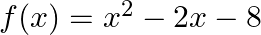and verify the relation between its zeroes and coefficients.$x^{2}-2 x-8=0$ $\Rightarrow \mathrm{x}^{2}-4 \mathrm{x}+2 \mathrm{x}-8=0$ $\Rightarrow x(x-4)+2(x-4)=0$ $\Rightarrow(x-4)(x+2)=0$ $\Rightarrow(x-4)=0$ or $(x+2)=0$ $\Rightarrow x=4$ or $x=-2$ Sum...
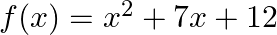and verify the relation between its zeroes and coefficients.$x^{2}+7 x+12=0$ $\Rightarrow x^{2}+4 x+3 x+12=0$ $\Rightarrow x(x+4)+3(x+4)=0$ $\Rightarrow(x+4)(x+3)=0$ $\Rightarrow(x+4)=0$ or $(x+3)=0$ $\Rightarrow \mathrm{x}=-4$ or $\mathrm{x}=-3$ Sum of...