$p(x)=3 x^{4}+5 x^{3}-7 x^{2}+2 x+2$ Dividing $p(x)$ by $\left(x^{2}+3 x+1\right)$, we have $$ \begin{gathered} \left.x^{2}+3 x+1\right) \begin{array}{l} 3 x^{4}+5 x^{3}-7 x^{2}+2 x+2 \\ 3 x^{4}+9...
Find the quotient when
Using remainder theorem, find the remainder when 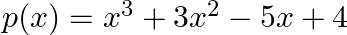 is divided by
is divided by 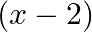
$p(x)=x^{3}+3 x^{2}-5 x+4$ $p(2)=2^{3}+3\left(2^{2}\right)-5(2)+4$ $=8+12-10+4$ $=14$
Find a cubic polynomial whose zeroes are 3,5 and 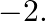
$\boldsymbol{\alpha}, \boldsymbol{\beta}$ and $\gamma$ are the zeroes of the required polynomial. $\boldsymbol{\alpha}+\boldsymbol{\beta}+\boldsymbol{\gamma}=3+5+(-2)=6$ $\boldsymbol{\alpha}...
If 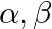 are the zeros of
are the zeros of 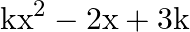 is equal
is equal 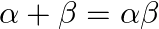 then
then 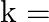 ? (a)
? (a) 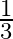 (b)
(b) 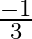 (c)
(c) 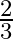 (d)
(d) 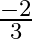
The correct option is option (c) $\frac{2}{3}$ $p(x)=x^{2}-2 x+3 k$ Comparing the given polynomial with $a x^{2}+b x+c$, we get: $a=1, b=-2$ and $c=3 k$ It is given that $\boldsymbol{\alpha}$ and...
If 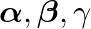 be the zeroes of the polynomial
be the zeroes of the polynomial 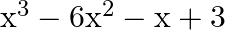 , then the values of
, then the values of 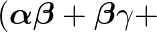
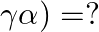 (a)
(a) 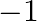 (b) 1 (c)
(b) 1 (c) 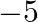 (d) 3
(d) 3
The correct option is option (a) $-1$ $p(x)=x^{3}-6 x^{2}-x+3$ Comparing the given polynomial with $\mathrm{x}^{3}-(\boldsymbol{\alpha}+\boldsymbol{\beta}+\gamma) \mathrm{x}^{2}+(\boldsymbol{\alpha}...
Which of the following is a true statement? (a) 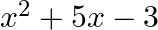 is a linear polynomial. (b)
is a linear polynomial. (b) 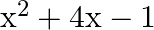 is a binomial (c)
is a binomial (c) 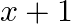 is a monomial (d)
is a monomial (d) 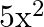 is a monomial
is a monomial
The correct option is option (d) $5 \mathrm{x}^{2}$ is a monomial. $5 \mathrm{x}^{2}$ consists of one term only. So, it is a monomial.
If one of the zeroes of the cubic polynomial 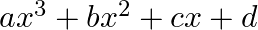 is 0 , then the product of the other two zeroes is (a)
is 0 , then the product of the other two zeroes is (a) 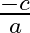 (b)
(b) 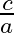 (c) 0 (d)
(c) 0 (d) 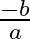
The correct option is option (b) $\frac{c}{a}$ $\alpha, \beta$ and 0 be the zeroes of $a x^{3}+b x^{2}+c x+d$. Then, sum of the products of zeroes taking two at a time is given by $(\alpha...
If 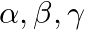 be the zeroes of the polynomial
be the zeroes of the polynomial 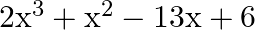 , then
, then 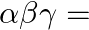 ? (a)
? (a) 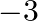 (b) 3 (c)
(b) 3 (c) 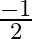 (d)
(d) 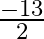
The correct option is option (a) $-3$ $\alpha, \beta$ and $\gamma$ are the zeroes of $2 \mathrm{x}^{3}+\mathrm{x}^{2}-13 \mathrm{x}+6$, we have: $\alpha \beta \gamma=\frac{-(\text { constant term...
If one zero of 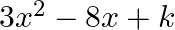 be the reciprocal of the other, then
be the reciprocal of the other, then 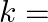 ? (a) 3 (b)
? (a) 3 (b) 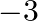 (c)
(c) 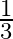 (d)
(d) 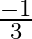
The correct option is option (a) $\mathrm{k}=3$ $\alpha$ and $\frac{1}{\alpha}$ be the zeroes of $3 x^{2}-8 x+k$. Then the product of zeroes $=\frac{k}{3}$ $\Rightarrow \alpha \times...
If one zero of the quadratic polynomial 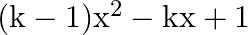 is
is 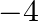 , then the value of
, then the value of 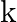 is (a)
is (a) 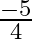 (b)
(b) 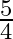 (c)
(c) 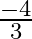 (d)
(d) 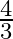
The correct option is option (b) $\frac{5}{4}$ Since $-4$ is a zero of $(k-1) x^{2}+k x+1$ $(k-1) \times(-4)^{2}+k \times(-4)+1=0$ $\Rightarrow 16 \mathrm{k}-16-4 \mathrm{k}+1=0$ $\Rightarrow 12...
If 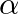 and
and 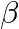 are the zeroes of
are the zeroes of 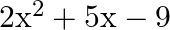 , then the value of
, then the value of 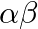 is (a)
is (a) 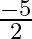 (b)
(b) 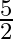 (c)
(c) 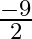 (d)
(d) 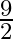
The correct option is option (c) $\frac{-9}{2}$ $\alpha$ and $\beta$ be the zeroes of $2 \mathrm{x}^{2}+5 \mathrm{x}-9$. If $\alpha+\beta$ are the zeroes, then $\mathrm{x}^{2}-(\alpha+\beta)...
If 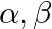 are the zeroes of the polynomial
are the zeroes of the polynomial 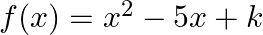 such that
such that 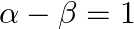 , find the value of
, find the value of 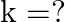
using the relationship between the zeroes of the quadratic polynomial. Sum of zeroes $=\frac{-(\text { coef ficient of } x)}{\text { coefficient of } x^{2}}$ and Product of zeroes $=\frac{\text {...
If the sum of the zeroes of the quadratic polynomial 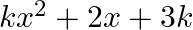 is equal to the product of its zeroes, then
is equal to the product of its zeroes, then 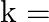 ? (a)
? (a) 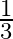 (b)
(b) 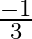 (c)
(c) 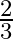 (d)
(d) 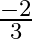
The correct option is option (d) $\frac{-2}{3}$ Assuming $\alpha$ and $\beta$ be the zeroes of $\mathrm{kx}^{2}+2 \mathrm{x}+3 \mathrm{k}$. Then $\alpha+\beta=\frac{-2}{k}$ and $\alpha \beta=3$...
If 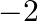 and 3 are the zeroes of the quadratic polynomial
and 3 are the zeroes of the quadratic polynomial 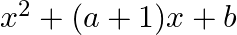 , then (a)
, then (a)  (b)
(b) 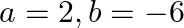 (c)
(c) 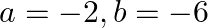 (d)
(d) 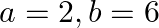
The correct option is option (c) $a=-2, b=-6$ Since, $-2$ and 3 are the zeroes of $x^{2}+(a+1) x+b$. $(-2)^{2}+(a+1) \times(-2)+b=0 \Rightarrow 4-2 a-2+b=0$ $\Rightarrow b-2 a=-2$….(1) Also,...
If 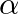 and
and 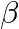 are the zeros of
are the zeros of  , then the value of
, then the value of 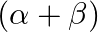 is (a) 5 (b)
is (a) 5 (b) 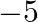 (c) 8 (d)
(c) 8 (d) 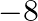
The correct option is option (b) $-5$ Since, $\alpha$ and $\beta$ be the zeroes of $\mathrm{x}^{2}+5 \mathrm{x}+8$. If $\alpha+\beta$ is the sum of the roots and $\alpha \beta$ is the product, then...
A quadratic polynomial whose zeroes are 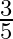 and
and 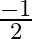 , is (a)
, is (a) 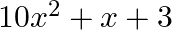 (b)
(b) 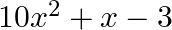 (c)
(c) 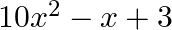 (d)
(d) 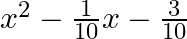
The correct option is option (d) $x^{2}-\frac{1}{10} x-\frac{3}{10}$ the zeroes are $\frac{3}{5}$ and $\frac{-1}{2}$ Let $\alpha=\frac{3}{5}$ and $\beta=\frac{-1}{2}$ sum of the zeroes,...
The sum and product of the zeroes of a quadratic polynomial are 3 and 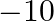 respectively. The quadratic polynomial is (a)
respectively. The quadratic polynomial is (a) 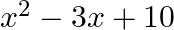 (b)
(b) 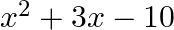 (c)
(c) 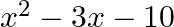 (d)
(d) 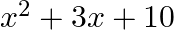
The correct option is option (c) $x^{2}-3 x-10$ Since, sum of zeroes, $\alpha+\beta=3$ Also, product of zeroes, $\alpha \beta=-10$ $\therefore$ Required polynomial...
The zeros of the polynomial 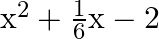 are (a)
are (a) 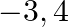 (b)
(b) 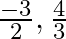 (c)
(c) 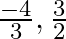 (d) none of these
(d) none of these
The correct option is option (b) $\frac{-3}{2}, \frac{4}{3}$ Let $f(x)=x^{2}+\frac{1}{6} x-2=0$ $\Rightarrow 6 \mathrm{x}^{2}+\mathrm{x}-12=0$ $\Rightarrow 6 x^{2}+9 x-8 x-12=0$ $\Rightarrow 3 x(2...
The zeroes of the polynomial 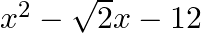 are (a)
are (a) 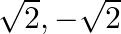 (b)
(b) 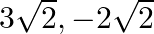 (c)
(c) 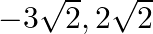 (d)
(d) 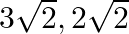
The correct option is option (b) $3 \sqrt{2},-2 \sqrt{2}$ Let $f(x)=x^{2}-\sqrt{2} x-12=0$ $\Rightarrow x^{2}-3 \sqrt{2} x+2 \sqrt{2} x-12=0$ $\Rightarrow x(x-3 \sqrt{2})+2 \sqrt{2}(x-3 \sqrt{2})=0$...
If 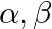 are the zeroes of the polynomial
are the zeroes of the polynomial 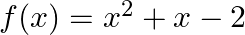 , then
, then 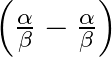 .
.
using the relationship between the zeroes of the quadratic polynomial. We have Sum of zeroes $=\frac{-(\text { coef ficient of } x)}{\text { coefficient of } x^{2}}$ and Product of zeroes...
If 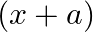 is a factor of
is a factor of 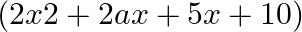 , then find the value of
, then find the value of 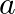
$(x+a)$ is a factor of $2 x^{2}+2 a x+5 x+10$ $x+a=0$ $\Rightarrow \mathrm{X}=-\mathrm{a}$ Since, $(x+a)$ is a factor of $2 x^{2}+2 a x+5 x+10$ Hence, It will satisfy the above polynomial...
If 1 is a zero of the quadratic polynomial 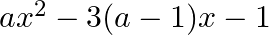 is 1 , then find the value of a.
is 1 , then find the value of a.
$x=1$ is one zero of the polynomial $a x^{2}-3(a-1) x-1$ Therefore, it will satisfy the above polynomial. Now, we have $a(1)^{2}-(a-1) 1-1=0$ $\Rightarrow a-3 a+3-1=0$ $\Rightarrow-2 \mathrm{a}=-2$...
If 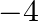 is a zero of the polynomial
is a zero of the polynomial 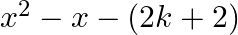 is
is 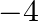 , then find the value of
, then find the value of  .
.
$x=-4$ is one zero of the polynomial $x^{2}-x-(2 k+2)$ Therefore, it will satisfy the above polynomial. Now, we have $(-4)^{2}-(-4)-(2 k+2)=0$ $\Rightarrow 16+4-2 \mathrm{k}-2=0$ $\Rightarrow 2...
Find the zeroes of the polynomial 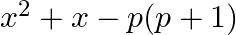
$f(x)=x^{2}+x-p(p+1)$ adding and subtracting $\mathrm{px}$, we get $f(x)=x^{2}+p x+x-p x-p(p+1)$ $=x^{2}+(p+1) x-p x-p(p+1)$ $=x[x+(p+1)]-p[x+(p+1)]$ $=[x+(p+1)](x-p)$ $f(x)=0$...
If one zero of the polynomial 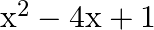 Is
Is 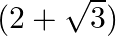 , write the other zero.
, write the other zero.
Let the other zeroes of $x^{2}-4 x+1$ be a (using the relationship between the zeroes of the quadratic polynomial) sum of zeroes $=\frac{-(\text { coef ficient of } x)}{\text { coef ficient of }...
Obtain all other zeroes of 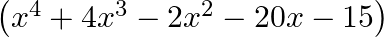 if two of its zeroes are
if two of its zeroes are 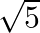 and
and 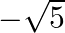 .
.
The given polynomial is $f(x)=x^{4}+4 x^{3}-2 x^{2}-20 x-15$. Since $(x-\sqrt{5})$ and $(x+\sqrt{5})$ are the zeroes of $f(x)$ it follows that each one of $(x-\sqrt{5})$ and $(x$ $+\sqrt{5})$ is a...
Verify division algorithm for the polynomial 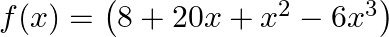 by
by 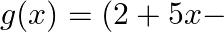
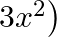
$-6 x^{3}+x^{2}+20 x+8$ and $g(x)$ as $-3 x^{2}+5 x+2$ Quotient $=2 \mathrm{x}+3$ Remainder $=x+2$ By using division rule, we have Dividend $=$ Quotient $\times$ Divisor $+$ Remainder $\therefore-6...
By actual division, show that 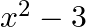 is a factor of
is a factor of 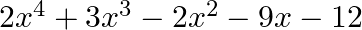 .
.
Let $f(x)=2 x^{4}+3 x^{3}-2 x^{2}-9 x-12$ and $g(x)$ as $x^{2}-3$
If 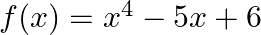 is divided by
is divided by 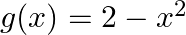 .
.
$f(x)$ as $x^{4}+0 x^{3}+0 x^{2}-5 x+6$ and $g(x) a s-x^{2}+2$ Quotient $q(x)=-x^{2}-2$ Remainder $\mathrm{r}(\mathrm{x})=-5 \mathrm{x}+10$
Find a cubic polynomial with the sum of its zeroes, sum of the products of its zeroes taken two at a time and the product of its zeroes as 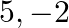 and
and 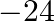 respectively.
respectively.
sum of the product of the zeroes taken two at a time and the product of the zeroes of a cubic polynomial then the cubic polynomial can be found as $x^{3}-($ sum of the zeroes $) x^{2}+($ sum of the...
Find a cubic polynomial whose zeroes are 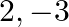 and
and 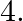
If the zeroes of the cubic polynomial are a, b and c then the cubic polynomial can be found as $x^{3}-(a+b+c) x^{2}+(a b+b c+c a) x-a b c$ Let $a=2, b=-3$ and $c=4$ Substituting the values in 1 , we...
Verify that 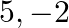 and
and 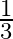 are the zeroes of the cubic polynomial
are the zeroes of the cubic polynomial 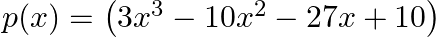 and verify the relation between its zeroes and coefficients.
and verify the relation between its zeroes and coefficients.
p(x)=3x3-10x2-27x+10 p(x)=\left(3 x^{3}-10 x^{2}-27 x+10\right) p(5)=3×53-10×52-27×5+10=(375-250-135+10)=0 p(5)=\left(3 \times 5^{3}-10 \times 5^{2}-27 \times...
Verify that 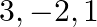 are the zeros of the cubic polynomial
are the zeros of the cubic polynomial 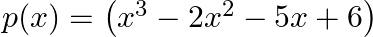 and verify the relation between it zeros and coefficients.
and verify the relation between it zeros and coefficients.
The given polynomial is $p(x)=\left(x^{3}-2 x^{2}-5 x+6\right)$ $$ \begin{aligned} &\therefore \mathrm{p}(3)=\left(3^{3}-2 \times 3^{2}-5 \times 3+6\right)=(27-18-15+6)=0 \\...
One zero of the polynomial 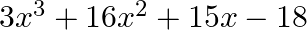 is
is 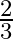 . Find the other zeros of the polynomial.
. Find the other zeros of the polynomial.
$x=\frac{2}{3}$ is one of the zero of $3 x^{3}+16 x^{2}+15 x-18$ Now, we have $\mathrm{x}=\frac{2}{3}$ $\Rightarrow \mathrm{x}-\frac{2}{3}=0$ Now, we divide $3 x^{3}+16 x^{2}+15 x-18$ by...
If 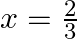 and
and 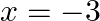 are the roots of the quadratic equation
are the roots of the quadratic equation 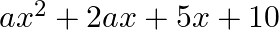 then find the value of a and
then find the value of a and 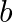 .
.
$a x^{2}+7 x+b=0$ Since, $x=\frac{2}{3}$ is the root of the above quadratic equation Hence, it will satisfy the above equation. => $a\left(\frac{2}{3}\right)^{2}+7\left(\frac{2}{3}\right)+b=0$...
Find the quadratic polynomial, sum of whose zeroes is 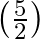 and their product is 1 . Hence, find the zeroes of the polynomial.
and their product is 1 . Hence, find the zeroes of the polynomial.
Let $\alpha$ and $\beta$ be the zeroes of the required polynomial $\mathrm{f}(\mathrm{x})$. =>$(\alpha+\beta)=\frac{5}{2}$ and $\alpha \beta=1$ $\therefore...
Find the quadratic polynomial, sum of whose zeroes is 8 and their product is 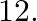 Hence, find the zeroes of the polynomial.
Hence, find the zeroes of the polynomial.
Let $\alpha$ and $\beta$ be the zeroes of the required polynomial $\mathrm{f}(\mathrm{x})$. Then $(\alpha+\beta)=8$ and $\alpha \beta=12$ $\therefore f(x)=x^{2}-(\alpha+\beta) x+\alpha \beta$...
Find the quadratic polynomial whose zeroes are 2 and 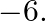 Verify the relation between the coefficients and the zeroes of the polynomial.
Verify the relation between the coefficients and the zeroes of the polynomial.
Let $\alpha=2$ and $\beta=-6$ Sum of the zeroes, $(\alpha+\beta)=2+(-6)=-4$ Product of the zeroes, $\alpha \beta=2 \times(-6)=-12$ $\therefore$ Required polynomial $=\mathrm{x}^{2}-(\alpha+\beta)...
Find the zeroes of the quadratic polynomial 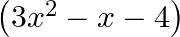 and verify the relation between the zeroes and the coefficients.
and verify the relation between the zeroes and the coefficients.
$$ \begin{aligned} &3 x^{2}-x-4=0 \\ &\Rightarrow 3 x^{2}-4 x+3 x-4=0 \\ &\Rightarrow x(3 x-4)+1(3 x-4)=0 \\ &\Rightarrow(3 x-4)(x+1)=0 \\ &\Rightarrow(3 x-4) \text { or }(x+1)=0 \\ &\Rightarrow...
Find the zeroes of the quadratic polynomial (5y 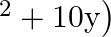 and verify the relation between the zeroes and the coefficients.
and verify the relation between the zeroes and the coefficients.
f(u)=5u2+10u \mathrm{f}(\mathrm{u})=5 \mathrm{u}^{2}+10 \mathrm{u} It can be written as $5 \mathrm{u}(\mathrm{u}+2)$ ∴f(u)=0⇒5u=0 or u+2=0 \therefore \mathrm{f}(\mathrm{u})=0...
Find the zeroes of the quadratic polynomial 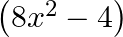 and verify the relation between the zeroes and the coefficients.
and verify the relation between the zeroes and the coefficients.
$$ \begin{aligned} &\mathrm{f}(\mathrm{x})=8 \mathrm{x}^{2}-4 \\ &\text { It can be written as } 8 \mathrm{x}^{2}+0 \mathrm{x}-4 \\ &=4\left\{(\sqrt{2} x)^{2}-(1)^{2}\right\} \\ &=4(\sqrt{2}...
Find the zeroes of the quadratic polynomial 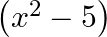 and verify the relation between the zeroes and the coefficients.
and verify the relation between the zeroes and the coefficients.
$$ \begin{aligned} &f(x)=x^{2}-5 \\ &\text { It can be written as } x^{2}+0 x-5 . \\ &=\left(x^{2}-(\sqrt{5})^{2}\right) \\ &=(x+\sqrt{5})(x-\sqrt{5}) \\ &\therefore f(x)=0...
Find the zeroes of the quadratic polynomial 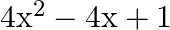 and verify the relation between the zeroes and the coefficients.
and verify the relation between the zeroes and the coefficients.
$$ \begin{aligned} &4 x^{2}-4 x+1=0 \\ &\Rightarrow(2 x)^{2}-2(2 x)(1)+(1)^{2}=0 \end{aligned} $$ $$ \begin{aligned} &\Rightarrow(2 \mathrm{x}-1)^{2}=0 \quad\left[\because \mathrm{a}^{2}-2...
Find the zeroes of the polynomial 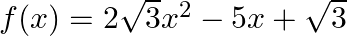 and verify the relation between its zeroes and coefficients.
and verify the relation between its zeroes and coefficients.
$$ \begin{aligned} &2 \sqrt{3} x^{2}-5 x+\sqrt{3} \\ &\Rightarrow 2 \sqrt{3} x^{2}-2 x-3 x+\sqrt{3} \\ &\Rightarrow 2 x(\sqrt{3} x-1)-\sqrt{3}(\sqrt{3} x-1)=0 \\ &\Rightarrow(\sqrt{3} x-1) \text {...
Find the zeroes of the quadratic polynomial 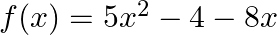 and verify the relationship between the zeroes and coefficients of the given polynomial.
and verify the relationship between the zeroes and coefficients of the given polynomial.
$f(x)=5 x^{2}-4-8 x$ $=5 x^{2}-8 x-4$ $=5 x^{2}-(10 x-2 x)-4$ $=5 x^{2}-10 x+2 x-4$ $=5 x(x-2)+2(x-2)$ $=(5 x+2)(x-2)$ $\therefore \mathrm{f}(\mathrm{x})=0 \Rightarrow(5...
Find the zeroes of the quadratic polynomial 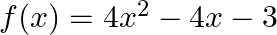 and verify the relation between its zeroes and coefficients.
and verify the relation between its zeroes and coefficients.
$f(x)=4 x^{2}-4 x-3$ $=4 x^{2}-(6 x-2 x)-3$ $=4 x^{2}-6 x+2 x-3$ $=2 x(2 x-3)+1(2 x-3)$ $=(2 x+1)(2 x-3)$ $\therefore \mathrm{f}(\mathrm{x})=0 \Rightarrow(2 \mathrm{x}+1)(2 \mathrm{x}-3)=0$...
Find the zeroes of the quadratic polynomial 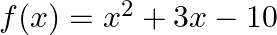 and verify the relation between its zeroes and coefficients.
and verify the relation between its zeroes and coefficients.
$f(x)=x^{2}+3 x-10$ $=x^{2}+5 x-2 x-10$ $=x(x+5)-2(x+5)$ $=(x-2)(x+5)$ $\therefore \mathrm{f}(\mathrm{x})=0 \Rightarrow(\mathrm{x}-2)(\mathrm{x}+5)=0$ $\Rightarrow x-2=0$ or $x+5=0$ $\Rightarrow...
Find the zeroes of the polynomial 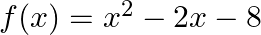 and verify the relation between its zeroes and coefficients.
and verify the relation between its zeroes and coefficients.
$x^{2}-2 x-8=0$ $\Rightarrow \mathrm{x}^{2}-4 \mathrm{x}+2 \mathrm{x}-8=0$ $\Rightarrow x(x-4)+2(x-4)=0$ $\Rightarrow(x-4)(x+2)=0$ $\Rightarrow(x-4)=0$ or $(x+2)=0$ $\Rightarrow x=4$ or $x=-2$ Sum...
Find the zeros of the polynomial 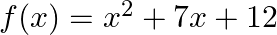 and verify the relation between its zeroes and coefficients.
and verify the relation between its zeroes and coefficients.
$x^{2}+7 x+12=0$ $\Rightarrow x^{2}+4 x+3 x+12=0$ $\Rightarrow x(x+4)+3(x+4)=0$ $\Rightarrow(x+4)(x+3)=0$ $\Rightarrow(x+4)=0$ or $(x+3)=0$ $\Rightarrow \mathrm{x}=-4$ or $\mathrm{x}=-3$ Sum of...
Obtain all other zeroes of 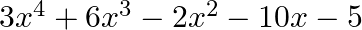 , if two of its zeroes are
, if two of its zeroes are 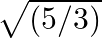 and
and 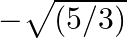
Due to the fact that this is a polynomial equation of degree 4, there will be a total of four roots. $V(5 / 3)$ and $-\sqrt{(5 / 3)}$ are zeroes of polynomial $f(x)$ $\therefore(x-\sqrt{(} 5 /...
On dividing 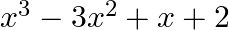 by a polynomial
by a polynomial 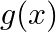 , the quotient and remainder were
, the quotient and remainder were 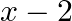 and
and 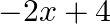 , respectively. Find
, respectively. Find 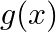
Solution: Given, Dividend, $p(x)=x^{3}-3 x^{2}+x+2$ Quotient $=x-2$ Remainder $=-2 x+4$ We must find the value of Divisor, $g(x)$ Concept: We already know that, Dividend = Divisor $\times$ Quotient...
Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0
Dividend p(x) and divisor g(x) are two polynomials, according to the division method, where g(x)=0. Then, using the formula below, we can get the value of the quotient q(x) and the remainder r(x);...
Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following:
![Rendered by QuickLaTeX.com \[\text { (i) } p(x)=x^{3}-3 x^{2}+5 x-3, g(x)=x^{2}-2\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d4dcd3ee9779f4b84bed2bef3209dcb1_l3.png)
![Rendered by QuickLaTeX.com \[\text { (ii) } p(x)=x^{4}-3 x^{2}+4 x+5, g(x)=x^{2}+1-x\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-baa8832c9a3a510eaa029756371b65a6_l3.png)
![Rendered by QuickLaTeX.com \[\text { (iii) } p(x)=x^{4}-5 x+6, g(x)=2-x^{2}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-31d1cd4548678d9def575c9a8b85541f_l3.png)
Solution: Solution: i) Given, Dividend $$=p(x)=x^{3}-3 x^{2}+5 x-3$$ Divisor $$=g(x)=x^{2}-2$$ We use long division method: Therefore, upon division we get, Quotient $=x-3$ Remainder $$=7 x-9$$ ii)...
Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
(i) 1/4 , -1
ii) √2, 1/3
iii) 0, √5
iv) 1, 1
v) -1/4, 1/4
vi) 4, 1
Solution: Concept: It is the zeros of a polynomial that correspond to the values of x that fulfil the equation y = f. (x). Here, f(x) is a function of x, and the zeros of the polynomial represent...
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
Solutions: Concept: When a polynomial is zeroed, the values of x that meet the equation y = f are considered zeros (x). There is a f(x) function, and the zeros of a polynomial are all of the values...
The graphs of y = p(x) are given in Fig. 2.10 below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.
Solutions: The following is a graphical way for finding zeroes:- When solving any polynomial equation, the total number of zeroes equals the total number of times the curve meets the x-axis. i) The...
