Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
If the points
If 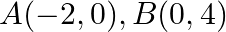 and
and 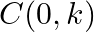 be three points such that area of a
be three points such that area of a  is 4 sq units, find the value of
is 4 sq units, find the value of  .
.
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the value of  for which the area of a ABC having vertices
for which the area of a ABC having vertices 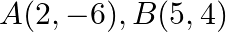 and
and 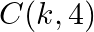 is 35 sq units.
is 35 sq units.
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the value of  for which the points
for which the points 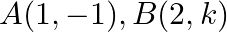 and
and 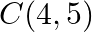 are collinear.
are collinear.
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the value of  for which the points
for which the points 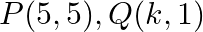 and
and 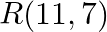 are collinear.
are collinear.
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the value of  for which the points
for which the points 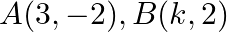 and
and 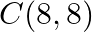 are collinear.
are collinear.
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Use determinants to show that the following points are collinear. 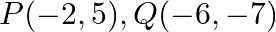 and
and 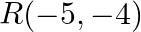
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Use determinants to show that the following points are collinear. 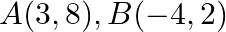 and
and 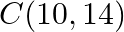
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Use determinants to show that the following points are collinear. 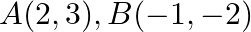 and
and 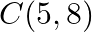
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the area of the triangle whose vertices are: 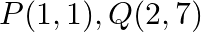 and
and 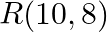
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the area of the triangle whose vertices are: 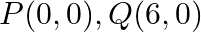 and
and 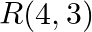
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the area of the triangle whose vertices are: 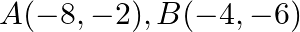 and
and 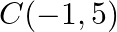
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the area of the triangle whose vertices are: 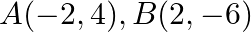 and
and 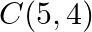
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the area of the triangle whose vertices are: 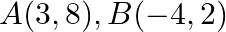 and
and 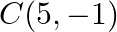
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Prove that: 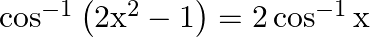
Solution: To Prove: $\cos ^{-1}\left(2 x^{2}-1\right)=2 \cos ^{-1} x$ Formula Used: $\cos 2 A=2 \cos ^{2} A-1$ Proof: $\text { LHS }=\cos ^{-1}\left(2 x^{2}-1\right) \ldots(1)$ Let $x=\cos A \ldots$...
Find the equation of a circle passing through the origin and intercepting lengths a and b on the axes.
Answer: AD = b units and AE = a units. D(0, b), E(a, 0) and A(0, 0) lies on the circle. C is the centre. The general equation of a circle: (x - h)2 + (y - k)2 = r2...
Using elementary row transformations, find the inverse of each of the following matrices: ![Rendered by QuickLaTeX.com \left[\begin{array}{ll} 4 & 0 \\ 2 & 5 \end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-00e067d8b3d687152537a9d78c193c7f_l3.png)
Solution: We have $A=\left(\begin{array}{ll}4 & 0 \\ 2 & 5\end{array}\right)$. To get the inverse we will proceed by augmented matrix with elementary row transformation process is as follow:...
Show that sec  is a continuous function.
is a continuous function.
Solution: Assume $f(x)=\sec x$ So, $f(x)=\frac{1}{\cos x}$ $f(x)$ is not defined when $\cos x=0$ And $\cos x=0$ when, $x=\frac{\pi}{2}$ and odd multiples of $\frac{\pi}{2}$ like $-\frac{\pi}{2}$...
Show that function 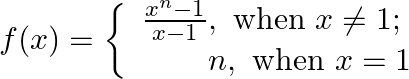
Solution: It is given that: $f(x)=\left\{\begin{array}{c} \frac{x^{n}-1}{x-1}, \text { when } x \neq 1 \\ n, \text { when } x=1 \end{array}\right.$ L.H.L. and $\mathrm{x}=1$ $\begin{array}{l} \lim...
Find the distance between the points (i) 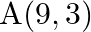 and
and 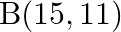 (ii)
(ii) 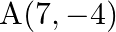 and
and 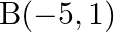
(i) $\quad \mathrm{A}(9,3)$ and $\mathrm{B}(15,11)$ The given points are $A(9,3)$ and $B(15,11)$. Then $\left(x_{1}=9, y_{1}=3\right)$ and $\left(x_{2}=15, y_{2}=11\right)$ $A...
Solve the system of equations by using the method of cross multiplication:
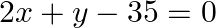
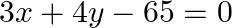
Solution: The given equations may be written as: $2 x+y-35=0\dots \dots(i)$ $3 \mathrm{x}+4 \mathrm{y}-65=0 \quad \ldots \ldots(ii)$ Here $a_{1}=2, b_{1}=1, c_{1}=-35, a_{2}=3, b_{2}=4$ and...
Solve the system of equations by using the method of cross multiplication:
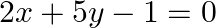 ,
,
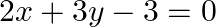
Solution: The given equations may be written as: $\begin{array}{l} 2 x+5 y-1=0\dots \dots(i) \\ 2 x+3 y-3=0\dots \dots(ii) \end{array}$ Here $a_{1}=2, b_{1}=5, c_{1}=-1, a_{2}=2, b_{2}=3$ and...
Solve the system of equations by using the method of cross multiplication:
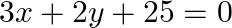 ,
,
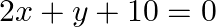
Solution: The given equations are: $3 x+2 y+25=0\dots \dots(i)$ $2 \mathrm{x}+\mathrm{y}+10=0 \quad \ldots \ldots(ii)$ Here $\mathrm{a}_{1}=3, \mathrm{~b}_{1}=2, \mathrm{c}_{1}=25, \mathrm{a}_{2}=2,...
Solve the system of equations by using the method of cross multiplication:
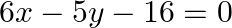
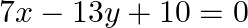
Solution: The given equations are: $\begin{array}{l} 6 x-5 y-16=0\dots \dots(i) \\ 7 x-13 y+10=0\dots \dots(ii) \end{array}$ Here $a_{1}=6, b_{1}=-5, c_{1}=-16, a_{2}=7, b_{2}=-13$ and $c_{2}=10$ On...
In the given, AB is the diameter of the circle with centre O. If ∠ADC = 32o, find angle BOC.
Solution: \[Arc\text{ }AC\text{ }subtends\angle AOC\]at the centre and \[\angle ADC\]at the remaining part of the circle. Thus, \[\angle AOC\text{ }=\text{ }2\angle ADC\] \[\angle AOC\text{ }=\text{...
In the given figure; ABC, AEQ and CEP are straight lines. Show that ∠APE and ∠CQE are supplementary.
Solution: Join \[EB\] Then, in cyclic quad. \[ABEP\] \[\angle APE\text{ }+\angle ABE\text{ }=\text{ }{{180}^{o}}~\ldots ..\text{ }\left( i \right)\][Opposite angles of a cyclic quad. are...
In the given figure, AB = AD = DC = PB and ∠DBC = xo. Determine, in terms of x: (i) ∠ABD, (ii) ∠APB. Hence or otherwise, prove that AP is parallel to DB.
Solution: Given, \[AB\text{ }=\text{ }AD\text{ }=\text{ }DC\text{ }=\text{ }PB\text{ }and~\angle DBC\text{ }=\text{ }{{x}^{o}}\] Join \[AC\text{ }and\text{ }BD\] Proof: \[\angle DAC\text{ }=\angle...
If I is the incentre of triangle ABC and AI when produced meets the circumcircle of triangle ABC in point D. If ∠BAC = 66o and ∠ABC = 80o. Calculate: ∠BIC
Solution: Join \[DB\text{ }and\text{ }DC,\text{ }IB\text{ }and\text{ }IC\] Given, if \[\angle BAC\text{ }=\text{ }{{66}^{o~}}and~\angle ABC\text{ }=~{{80}^{o}}\] \[I\] is the incentre of the...
If I is the incentre of triangle ABC and AI when produced meets the circumcircle of triangle ABC in point D. If ∠BAC = 66o and ∠ABC = 80o. Calculate: (i) ∠DBC, (ii) ∠IBC,
Solution: Join \[DB\text{ }and\text{ }DC,\text{ }IB\text{ }and\text{ }IC\] Given, if \[\angle BAC\text{ }=\text{ }{{66}^{o~}}and~\angle ABC\text{ }=~{{80}^{o}}\] \[I\] is the incentre of the...
In the given figure, ABCD is a cyclic quadrilateral. AF is drawn parallel to CB and DA is produced to point E. If ∠ADC = 92o, ∠FAE = 20o; determine ∠BCD. Given reason in support of your answer.
Solution: Given, In cyclic quad. \[ABCD\] \[AF\text{ }||\text{ }CB\text{ }and\text{ }DA\] is produced to \[E\]such that \[\angle ADC\text{ }=\text{ }{{92}^{o}}~and\angle FAE\text{ }=\text{...
D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Prove that the points B, C, E and D are concyclic.
Given, \[\vartriangle ABC,\text{ }AB\text{ }=\text{ }AC\text{ }and\text{ }D\text{ }and\text{ }E\]are points on \[AB\text{ }and\text{ }AC\]such that \[AD\text{ }=\text{ }AE\] And, \[DE\] is joined....
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate: ∠BAC
Solution: In cyclic quadrilateral \[ABEC\] \[\angle BAC\text{ }+\angle BEC\text{ }=\text{ }{{180}^{o}}~\] [Opposite angles of a cyclic quadrilateral are supplementary] \[\angle BAC\text{ }+\text{...
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate: (i) ∠BDC (ii) ∠BEC
Solution: (i) Given that \[BD\] is a diameter of the circle. And, the angle in a semicircle is a right angle. So, \[\angle BCD\text{ }=\text{ }90{}^\circ \] Also given that, \[\angle DBC\text{...
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic. Prove it.
Let \[ABCD\] be a cyclic quadrilateral and \[PQRS\] be the quadrilateral formed by the angle bisectors of angle \[\angle A,\angle B,\angle C\text{ }and\angle D\] Required to prove: \[PQRS\] is a...
In the given figure, chord ED is parallel to diameter AC of the circle. Given ∠CBE = 65o, calculate ∠DEC.
Solution: Join \[OE\] \[Arc\text{ }EC\] subtends \[\angle EOC\]at the centre and \[\angle EBC\]at the remaining part of the circle. \[\angle EOC\text{ }=\text{ }2\angle EBC\text{ }=\text{ }2\text{...
Prove that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
Suppose, \[\vartriangle ABC,\text{ }AB\text{ }=\text{ }AC\]and circle with \[AB\] as diameter is drawn which intersects the side \[BC\text{ }and\text{ }D\] And, join \[AD\] Proof: It’s seen that,...
In the given figure, ABC is a triangle in which ∠BAC = 30o. Show that BC is equal to the radius of the circum-circle of the triangle ABC, whose center is O.
Solution: Firstly, join \[OB\text{ }and\text{ }OC\] Proof: \[\angle BOC\text{ }=\text{ }2\angle BAC\text{ }=\text{ }2\text{ }x\text{ }{{30}^{o}}~=\text{ }{{60}^{o}}\] Now, in \[\vartriangle OBC\]...
In the given circle with diameter AB, find the value of x.
Solution: Now, \[\angle ABD\text{ }=\angle ACD\text{ }=\text{ }{{30}^{o}}~\][Angles in the same segment] In \[\vartriangle ADB\] by angle sum property we have \[\angle BAD\text{ }+\angle ADB\text{...
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centers. Find the radii of the three circles.
Solution: According to the given question, ABC is a triangle with \[AB\text{ }=\text{ }10\text{ }cm,\text{ }BC=\text{ }8\text{ }cm,\text{ }AC\text{ }=\text{ }6\text{ }cm\] Three circles are drawn...
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30degree, find: angle APB
Solution: In the given fig, \[O\]is the centre of the circle and, \[CA\text{ }and\text{ }CB\]are the tangents to the circle from \[C\]Also, \[\angle ACO\text{ }=\text{ }{{30}^{o}}\] \[P\] is any...
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30degree, find: (i) angle BCO (ii) angle AOB
Solution: In the given fig, \[O\]is the centre of the circle and, \[CA\text{ }and\text{ }CB\]are the tangents to the circle from \[C\]Also, \[\angle ACO\text{ }=\text{ }{{30}^{o}}\] \[P\] is any...
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC = 120degree Calculate: i) ∠BEC ii) ∠BED
i) Join \[OC\text{ }and\text{ }OB\] \[AB\text{ }=\text{ }BC\text{ }=\text{ }CD\] And \[\angle ABC\text{ }=\text{ }{{120}^{o}}~\][Given] So, \[\angle BCD\text{ }=\angle ABC\text{ }=\text{...
In the given figure, AC = AE. Show that: i) CP = EP ii) BP = DP
Solution: In \[\vartriangle ADC\text{ }and\text{ }\vartriangle ABE\] \[\angle ACD\text{ }=\angle AEB~\] [Angles in the same segment] \[AC\text{ }=\text{ }AE\][Given] \[\angle A\text{ }=\angle...
ABC is a right triangle with angle B = 90º. A circle with BC as diameter meets by hypotenuse AC at point D. Prove that: i) AC x AD = AB^2 ii) BD^2 = AD x DC.
i) In \[\vartriangle ABC\] We know that \[\angle B\text{ }=\text{ }{{90}^{o}}~and\text{ }BC\]is the diameter of the circle. Hence, \[AB\]is the tangent to the circle at \[B\] Now, as \[AB\] is...
The given figure shows a circle with centre O and BCD is a tangent to it at C. Show that: ∠ACD + ∠BAC = 90degree
Solution: Join \[OC\] \[BCD\]is the tangent and \[OC\]is the radius. As, \[OC\bot BD\] \[\angle OCD\text{ }=\text{ }{{90}^{o}}\] \[\angle OCD\text{ }+\angle ACD\text{ }=\text{ }{{90}^{o}}~\ldots...
In the given figure, ABCD is a cyclic quadrilateral, PQ is tangent to the circle at point C and BD is its diameter. If ∠DCQ = 40degree and ∠ABD = 60degree, find: ∠ADB
Solution: In \[\vartriangle ABD\] \[\angle BAD\text{ }=\text{ }{{90}^{o}}\] [Angle in a semi-circle], \[\angle ABD\text{ }=\text{ }{{60}^{o}}~\] [Given] Or, \[\angle ADB\text{ }=\text{...
In the given figure, ABCD is a cyclic quadrilateral, PQ is tangent to the circle at point C and BD is its diameter. If ∠DCQ = 40degree and ∠ABD = 60degree, find: i) ∠DBC ii) ∠BCP
Solution: 15. (i) \[PQ\]is a tangent and \[CD\]is a chord. \[\angle DCQ\text{ }=\angle DBC\] [Angles in the alternate segment] \[\angle DBC\text{ }=\text{ }{{40}^{o}}\] \[[As\angle DCQ\text{...
In the given figure, MN is the common chord of two intersecting circles and AB is their common tangent. Prove that the line NM produced bisects AB at P.
Solution: From \[P,\text{ }AP\] is the tangent And \[PMN\]is the secant for first circle. \[A{{P}^{2}}~=\text{ }PM\text{ }x\text{ }PN\text{ }\ldots .\text{ }\left( 1 \right)\] Again from \[P,\text{...
P is the midpoint of an arc APB of a circle. Prove that the tangent drawn at P will be parallel to the chord AB.
Join \[AP\text{ }and\text{ }BP\] As \[TPS\] is a tangent And \[PA\]is the chord of the circle. \[\angle BPT\text{ }=\angle PAB~\] [Angles in alternate segments] But, \[\angle PBA\text{ }=\angle...
Prove that the perimeter of a right triangle is equal to the sum of the diameter of its incircle and twice the diameter of its circumcircle.
Join \[OL,\text{ }OM\text{ }and\text{ }ON\] Suppose, \[D\text{ }and\text{ }d\] be the diameter of the circumcircle and incircle. Also, \[R\text{ }and\text{ }r\] be the radius of the circumcircle and...
In the figure, AB is the chord of a circle with centre O and DOC is a line segment such that BC = DO. If ∠C = 20degree, find angle AOD.
Solution: Join \[OB\] In \[\vartriangle OBC\] we have \[BC\text{ }=\text{ }OD\text{ }=\text{ }OB\][Radii of the same circle] \[\angle BOC\text{ }=\angle BCO\text{ }=\text{ }{{20}^{o}}\] And ext....
Bisectors of vertex angles A, B and C of a triangle ABC intersect its circumcircle at points D, E and F respectively. Prove that angle EDF = 90degree – ½ ∠A
Join \[ED,\text{ }EF\text{ }and\text{ }DF\] And \[BF,\text{ }FA,\text{ }AE\text{ }and\text{ }EC\] \[\angle EBF\text{ }=\angle ECF\text{ }=\angle EDF\text{ }\ldots ..\text{ }\left( i \right)\] [Angle...
Show that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
Join \[AD\] And \[AB\] is the diameter. We have \[\angle ADB\text{ }=\text{ }90{}^\text{o}~\][Angle in a semi-circle] But, \[\angle ADB\text{ }+~\angle ADC\text{ }=\text{ }180{}^\text{o}~\][Linear...
In cyclic quadrilateral ABCD, ∠A = 3 ∠C and ∠D = 5 ∠B. Find the measure of each angle of the quadrilateral.
Given, cyclic quadrilateral \[ABCD\] So, \[\angle A\text{ }+\angle C\text{ }=\text{ }{{180}^{o}}~\][Opposite angles in a cyclic quadrilateral is supplementary] \[3\angle C\text{ }+\angle C\text{...
In the given figure, C and D are points on the semi-circle described on AB as diameter. Given angle BAD = 70degree and angle DBC = 30degree, calculate angle BDC.
Solution: \[ABCD\] is a cyclic quadrilateral, \[\angle BCD\text{ }+~\angle BAD\text{ }=\text{ }{{180}^{\circ }}\] [Opposite angles of a cyclic quadrilateral are supplementary] \[\angle BCD\text{...
ABCD is a cyclic quadrilateral in which BC is parallel to AD, angle ADC = 110o and angle BAC = 50o. Find angle DAC and angle DCA.
Given, \[ABCD\] is a cyclic quadrilateral in which \[AD\text{ }||\text{ }BC\] And, \[\angle ADC\text{ }=\text{ }{{110}^{o}},\angle BAC\text{ }=\text{ }{{50}^{o}}\] We know that, \[\angle B\text{...
The diameter and a chord of circle have a common end-point. If the length of the diameter is 20 cm and the length of the chord is 12 cm, how far is the chord from the center of the circle?
We have, \[AB\]as the diameter and \[AC\]as the chord. Now, draw \[OL\bot AC\] Since\[OL\bot AC\] and hence it bisects \[AC\] \[O\] is the centre of the circle. Therefore, \[OA\text{ }=\text{...
Two chords AB and AC of a circle are equal. Prove that the center of the circle, lies on the bisector of the angle BAC.
Given: \[AB\text{ }and\text{ }AC\] are two equal chords of \[C\text{ }\left( O,\text{ }r \right)\] Required to prove: Centre, \[O\] lies on the bisector of \[\angle BAC\] Construction: Join \[BC\]...
Two circles with centers A and B, and radii 5 cm and 3 cm, touch each other internally. If the perpendicular bisector of the segment AB meets the bigger circle in P and Q; find the length of PQ.
We know that, If two circles touch internally, then distance between their centres is equal to the difference of their radii. So, \[AB\text{ }=\text{ }\left( 5\text{ }-\text{ }3 \right)\text{...
OABC is a rhombus whose three vertices A, B and C lie on a circle with centre O. i) If the radius of the circle is 10 cm, find the area of the rhombus. ii) If the area of the rhombus is 32√3 cm2, find the radius of the circle.
(i) Given, \[radius\text{ }=\text{ }10\text{ }cm\] In rhombus \[OABC\] \[OC\text{ }=\text{ }10\text{ }cm\] So,...
Prove that, of any two chords of a circle, the greater chord is nearer to the center.
Given: \[A\] circle with center \[O\] and radius \[r\] \[AB\text{ }and\text{ }CD\]are two chords such that \[AB\text{ }>\text{ }CD\] Also, \[OM\bot AB\text{ }and\text{ }ON\bot CD\] Required to...
Two circles touch each other internally at a point P. A chord AB of the bigger circle intersects the other circle in C and D. Prove that: ∠CPA = ∠DPB
Solution: Let’s draw a tangent \[TS\text{ }at\text{ }P\]to the circles given. As \[TPS\]is the tangent and \[PD\]is the chord, we have \[\angle PAB\text{ }=\angle BPS\text{ }\ldots .\text{ }\left( i...
Two circles with centres O and O’ are drawn to intersect each other at points A and B. Centre O of one circle lies on the circumference of the other circle and CD is drawn tangent to the circle with centre O’ at A. Prove that OA bisects angle BAC.
Solution: Join \[OA,\text{ }OB,\text{ }OA,\text{ }OB\text{ }and\text{ }OO\] \[CD\]is the tangent and \[AO\]is the chord. \[\angle OAC\text{ }=\angle OBA\text{ }\ldots \text{ }\left( i \right)\] ...
Tangent at P to the circumcircle of triangle PQR is drawn. If this tangent is parallel to side QR, show that triangle PQR is isosceles.
Let \[DE\]be the tangent to the circle at \[P\] And, \[DE\text{ }||\text{ }QR\][Given] \[\angle EPR\text{ }=\angle PRQ\][Alternate angles are equal] \[\angle DPQ\text{ }=\angle PQR\][Alternate...
One card is drawn from a well shuffled deck of 52 cards. Find the probability of getting: (v) a diamond or a spade
(v) Number of favorable outcomes for a diamond or a spade = 13 + 13 = 26 So, number of favorable outcomes = 26 Hence, P(getting a diamond or a spade) = 26/52 = 1/2
One card is drawn from a well shuffled deck of 52 cards. Find the probability of getting: (iii) the jack or the queen of the hearts (iv) a diamond
(iii) Favorable outcomes for jack or queen of hearts = 1 jack + 1 queen So, the number of favorable outcomes = 2 Hence, P(jack or queen of hearts) = 2/52 = 1/26 (iv) Number of favorable outcomes for...
One card is drawn from a well shuffled deck of 52 cards. Find the probability of getting: (i) a queen of red color (ii) a black face card
Solution: We have, Total possible outcomes = 52 (i) Number queens of red color = 2 Number of favorable outcomes = 2 Hence, P(queen of red color) = 2/52 (ii) Number of black cards = 26 Number of...
A game consists of spinning arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12; as shown below.If the outcomes are equally likely, find the probability that the pointer will point at: (v) a number less than or equal to 9 (vi) a number between 3 and 11
(v) Favorable outcomes for a number less than or equal to 9 are 1, 2, 3, 4, 5, 6, 7, 8, 9 So, number of favorable outcomes = 9 Hence, P(the pointer will be at a number less than or equal to 9) =...
A game consists of spinning arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12; as shown below.If the outcomes are equally likely, find the probability that the pointer will point at: (iii) a prime number (iv) a number greater than 8
(iii) Favorable outcomes for a prime number are 2, 3, 5, 7, 11 So, number of favorable outcomes = 5 Hence, P(the pointer will be at a prime number) = 5/12 (iv) Favorable outcomes for a number...
A game consists of spinning arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12; as shown below.If the outcomes are equally likely, find the probability that the pointer will point at: (i) 6 (ii) an even number
Solution: We have, Total number of possible outcomes = 12 (i) Number of favorable outcomes for 6 = 1 Hence, P(the pointer will point at 6) = 1/12 (ii) Favorable outcomes for an even number are 2, 4,...
A bag contains twenty Rs 5 coins, fifty Rs 2 coins and thirty Re 1 coins. If it is equally likely that one of the coins will fall down when the bag is turned upside down, what is the probability that the coin: (i) will be a Re 1 coin? (ii) will not be a Rs 2 coin? (iii) will neither be a Rs 5 coin nor be a Re 1 coin?
(iii) Number of favourable outcomes for neither Re 1 nor Rs 5 coins = Number of favourable outcomes for Rs 2 coins = 50 = n(E) Hence, probability (neither Re 1 nor Rs 5 coin) = n(E)/ n(S) = 50/100 =...
A bag contains twenty Rs 5 coins, fifty Rs 2 coins and thirty Re 1 coins. If it is equally likely that one of the coins will fall down when the bag is turned upside down, what is the probability that the coin: (i) will be a Re 1 coin? (ii) will not be a Rs 2 coin?
Solution: We have, Total number of coins = 20 + 50 + 30 = 100 So, the total possible outcomes = 100 = n(S) (i) Number of favourable outcomes for Re 1 coins = 30 = n(E) Probability (Re 1 coin) =...
A bag contains 10 red balls, 16 white balls and 8 green balls. A ball is drawn out of the bag at random. What is the probability that the ball drawn will be: (iii) white or green?
(iii) Number of favorable outcomes for white or green ball = 16 + 8 = 24 = n(E) Hence, probability for drawing a white or green ball = n(E)/ n(S) = 24/34 = 12/17
A bag contains 10 red balls, 16 white balls and 8 green balls. A ball is drawn out of the bag at random. What is the probability that the ball drawn will be: (i) not red? (ii) neither red nor green?
Solution: Total number of possible outcomes = 10 + 16 + 8 = 34 balls So, n(S) = 34 (i) Favorable outcomes for not a red ball = favorable outcomes for white or green ball So, number of favorable...
The probability that two boys do not have the same birthday is 0.897. What is the probability that the two boys have the same birthday?
Solution: We know that, P(do not have the same birthday) + P(have same birthday) = 1 0.897 + P(have same birthday) = 1 Thus, P(have same birthday) = 1 – 0.897 P(have same birthday) =...
A bag contains a certain number of red balls. A ball is drawn. Find the probability that the ball drawn is: (i) black (ii) red
Solution: We have, Total possible outcomes = number of red balls. (i) Number of favourable outcomes for black balls = 0 Hence, P(black ball) = 0 (ii) Number of favourable outcomes for red balls =...
If P(E) = 0.59; find P(not E)
Solution: We know that, P(E) + P(not E) = 1 So, 0.59 + P(not E) = 1 Hence, P(not E) = 1 – 0.59 = 0.41
Which of the following cannot be the probability of an event? (iii) 37% (iv) -2.4
(iii) As 0 ≤ 37 % = (37/100) ≤ 1 Thus, 37 % can be a probability of an event. (iv) As -2.4 < 0 Thus, -2.4 cannot be a probability of an event.
Which of the following cannot be the probability of an event? (i) 3/7 (ii) 0.82
Solution: We know that probability of an event E is 0 ≤ P(E) ≤ 1 (i) As 0 ≤ 3/7 ≤ 1 Thus, 3/7 can be a probability of an event. (ii) As 0 ≤ 0.82 ≤ 1 Thus, 0.82 can be a probability of an...
Two dice are thrown at the same time. Find the probability that the sum of the two numbers appearing on the top of the dice is:(iii) less than or equal to 12
(iii) All the outcomes are favourable to the event E = ‘sum of two numbers ≤ 12’. Thus, P(E) = n(E)/ n(S) = 36/36 = 1
Two dice are thrown at the same time. Find the probability that the sum of the two numbers appearing on the top of the dice is: (i) 8 (ii) 13
Solution: We have, the number of possible outcomes = 6 × 6 = 36. (i) The outcomes favourable to the event ‘the sum of the two numbers is 8’ = E = {(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)} The number...
In a bundle of 50 shirts, 44 are good, 4 have minor defects and 2 have major defects. What is the probability that: (i) it is acceptable to a trader who accepts only a good shirt? (ii) it is acceptable to a trader who rejects only a shirt with major defects?
Solution: We have, Total number of shirts = 50 Total number of elementary events = 50 = n(S) (i) As, trader accepts only good shirts and number of good shirts = 44 Event of accepting good shirts =...
In a musical chairs game, a person has been advised to stop playing the music at any time within 40 seconds after its start. What is the probability that the music will stop within the first 15 seconds?
Solution: Total result = 0 sec to 40 sec Total possible outcomes = 40 So, n(S) = 40 Favourable results = 0 sec to 15 sec Favourable outcomes = 15 So, n(E) = 15 Hence, the probability that the music...
All the three face cards of spades are removed from a well shuffled pack of 52 cards. A card is then drawn at random from the remaining pack. Find the probability of getting:(iii) a black card
(iii) Number of black cards left = 23 cards (13 club + 10 spade) Event of drawing a black card = E = 23 So, n(E) = 23 Hence, probability of drawing a black card = n(E)/ n(S) = 23/49
All the three face cards of spades are removed from a well shuffled pack of 52 cards. A card is then drawn at random from the remaining pack. Find the probability of getting: (i) a black face card (ii) a queen
Solution: We have, Total number of cards = 52 If 3 face cards of spades are removed Then, the remaining cards = 52 – 3 = 49 = number of possible outcomes So, n(S) = 49 (i) Number of black face cards...
A box contains 7 red balls, 8 green balls and 5 white balls. A ball is drawn at random from the box. Find the probability that the ball is: (i) white (ii) neither red nor white.
Solution: We have, Total number of balls in the box = 7 + 8 + 5 = 20 balls Total possible outcomes = 20 = n(S) (i) Event of drawing a white ball = E = number of white balls = 5 So, n(E) = 5 Hence,...
A and B are friends. Ignoring the leap year, find the probability that both friends will have: (i) different birthdays? (ii) the same birthday?
Solution: Out of the two friends, A’s birthday can be any day of the year. Now, B’s birthday can also be any day of 365 days in the year. We assume that these 365 outcomes are equally likely. So,...
In a match between A and B: (i) the probability of winning of A is 0.83. What is the probability of winning of B? (ii) the probability of losing the match is 0.49 for B. What is the probability of winning of A?
Solution: (i) We know that, The probability of winning of A + Probability of losing of A = 1 And, Probability of losing of A = Probability of winning of B Therefore, Probability of winning of A +...
From a well shuffled deck of 52 cards, one card is drawn. Find the probability that the card drawn is:(v) a card with number less than 8 (vi) a card with number between 2 and 9
(v) Numbers less than 8 = { 2, 3, 4, 5, 6, 7} Event of drawing a card with number less than 8 = E = {6H cards, 6D cards, 6S cards, 6C cards} So, n(E) = 24 Thus, probability of drawing a card with...
From a well shuffled deck of 52 cards, one card is drawn. Find the probability that the card drawn is: (iii) a queen of black card (iv) a card with number 5 or 6
(iii) Event of drawing a queen of black colour = {Q(spade), Q(club)} = E So, n(E) = 2 Thus, probability of drawing a queen of black colour = n(E)/ n(S) = 2/52 = 1/26 (iv) Event of drawing a card...
From a well shuffled deck of 52 cards, one card is drawn. Find the probability that the card drawn is: (i) a face card (ii) not a face card
Solution: We have, the total number of possible outcomes = 52 So, n(S) = 52 (i) No. of face cards in a deck of 52 cards = 12 (4 kings, 4 queens and 4 jacks) Event of drawing a face cards = E = (4...
A dice is thrown once. What is the probability of getting a number: (i) greater than 2? (ii) less than or equal to 2?
Solution: The number of possible outcomes when dice is thrown = {1, 2, 3, 4, 5, 6} So, n(S) = 6 (i) Event of getting a number greater than 2 = E = {3, 4, 5, 6} So, n(E) = 4 Thus, probability of...
A bag contains 3 red balls, 4 blue balls and 1 yellow ball, all the balls being identical in shape and size. If a ball is taken out of the bag without looking into it; find the probability that the ball is: (iii) not yellow (iv) neither yellow nor red
(iii) Probability of not drawing a yellow ball = 1 – Probability of drawing a yellow ball Thus, probability of not drawing a yellow ball = 1 – 1/8 = (8 – 1)/ 8 = 7/8 (iv) Neither yellow ball nor red...
A bag contains 3 red balls, 4 blue balls and 1 yellow ball, all the balls being identical in shape and size. If a ball is taken out of the bag without looking into it; find the probability that the ball is: (i) yellow (ii) red
Solution: The total number of balls in the bag = 3 + 4 + 1 = 8 balls So, the number of possible outcomes = 8 = n(S) (i) Event of drawing a yellow ball = {Y} So, n(E) = 1 Thus, probability of drawing...
If two coins are tossed once, what is the probability of getting: (iii) both heads or both tails.
(iii) E = event of getting both heads or both tails = {HH, TT} n(E) = 2 Hence, probability of getting both heads or both tails = n(E)/ n(S) = 2/4 = ½
If two coins are tossed once, what is the probability of getting: (i) both heads. (ii) at least one head.
Solution: We know that, when two coins are tossed together possible number of outcomes = {HH, TH, HT, TT} So, n(S) = 4 (i) E = event of getting both heads = {HH} n(E) = 1 Hence, probability of...
A pair of dice is thrown. Find the probability of getting a sum of 10 or more, if 5 appears on the first die.
Solution: In throwing a dice, total possible outcomes = {1, 2, 3, 4, 5, 6} So, n(S) = 6 For two dice, n(S) = 6 x 6 = 36 Favorable cases where the sum is 10 or more with 5 on 1st die = {(5, 5), (5,...
A book contains 85 pages. A page is chosen at random. What is the probability that the sum of the digits on the page is 8?
Solution: We know that, Number of pages in the book = 85 Number of possible outcomes = n(S) = 85 Out of 85 pages, pages that sum up to 8 = {8, 17, 26, 35, 44, 53, 62, 71, 80} So, pages that sum up...
A die is thrown once. Find the probability of getting a number: (iii) less than 8 (iv) greater than 6
(iii) On a dice, numbers less than 8 = {1, 2, 3, 4, 5, 6} So, n(E) = 6 Hence, probability of getting a number less than 8 = n(E)/ n(S) = 6/6 = 1 (iv) On a dice, numbers greater than 6 = 0 So, n(E) =...
A die is thrown once. Find the probability of getting a number: (i) less than 3 (ii) greater than or equal to 4
Solution: We know that, In throwing a dice, total possible outcomes = {1, 2, 3, 4, 5, 6} So, n(S) = 6 (i) On a dice, numbers less than 3 = {1, 2} So, n(E) = 2 Hence, probability of getting a number...
From 25 identical cards, numbered 1, 2, 3, 4, 5, ……, 24, 25: one card is drawn at random. Find the probability that the number on the card drawn is a multiple of: (iii) 3 and 5 (iv) 3 or 5
(iii) From numbers 1 to 25, there is only one number which is multiple of 3 and 5 i.e. {15} So, favorable number of events = n(E) = 1 Hence, probability of selecting a card with a multiple of 3 and...
From 25 identical cards, numbered 1, 2, 3, 4, 5, ……, 24, 25: one card is drawn at random. Find the probability that the number on the card drawn is a multiple of: (i) 3 (ii) 5
Solution: We know that, there are 25 cards from which one card is drawn. So, the total number of elementary events = n(S) = 25 (i) From numbers 1 to 25, there are 8 numbers which are multiple of 3...
Hundred identical cards are numbered from 1 to 100. The cards The cards are well shuffled and then a card is drawn. Find the probability that the number on card drawn is: (v) less than 48
(v) From numbers 1 to 100, there are 47 numbers which are less than 48 i.e. {1, 2, ……….., 46, 47} So, favorable number of events = n(E) = 47 Hence, probability of selecting a card with a number less...
Hundred identical cards are numbered from 1 to 100. The cards The cards are well shuffled and then a card is drawn. Find the probability that the number on card drawn is: (iii) between 40 and 60 (iv) greater than 85
(iii) From numbers 1 to 100, there are 19 numbers which are between 40 and 60 i.e. {41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59} So, favorable number of events = n(E)...
Hundred identical cards are numbered from 1 to 100. The cards The cards are well shuffled and then a card is drawn. Find the probability that the number on card drawn is: (i) a multiple of 5 (ii) a multiple of 6
Solution: We kwon that, there are 100 cards from which one card is drawn. Total number of elementary events = n(S) = 100 (i) From numbers 1 to 100, there are 20 numbers which are multiple of 5...
Nine cards (identical in all respects) are numbered 2 to 10. A card is selected from them at random. Find the probability that the card selected will be:(iii) an even number and a multiple of 3 (iv) an even number or a multiple of 3
(iii) From numbers 2 to 10, there is one number which is an even number as well as multiple of 3 i.e. 6 So, favorable number of events = n(E) = 1 Hence, probability of selecting a card with a number...
Nine cards (identical in all respects) are numbered 2 to 10. A card is selected from them at random. Find the probability that the card selected will be: (i) an even number (ii) a multiple of 3
Solution: We know that, there are totally 9 cards from which one card is drawn. Total number of elementary events = n(S) = 9 (i) From numbers 2 to 10, there are 5 even numbers i.e. 2, 4, 6, 8, 10...
In a T.T. match between Geeta and Ritu, the probability of the winning of Ritu is 0.73. Find the probability of: (i) winning of Geeta (ii) not winning of Ritu
Solution: (i) Winning of Geeta is a complementary event to winning of Ritu Thus, P(winning of Ritu) + P(winning of Geeta) = 1 P(winning of Geeta) = 1 – P(winning of Ritu) P(winning of Geeta) =...
(i) If A and B are two complementary events then what is the relation between P(A) and P(B)? (ii) If the probability of happening an event A is 0.46. What will be the probability of not happening of the event A?
Solution: (i) Two complementary events, taken together, include all the outcomes for an experiment and the sum of the probabilities of all outcomes is 1. P(A) + P(B) = 1 (ii) P(A) = 0.46 Let P(B) be...
From a well shuffled deck of 52 cards, one card is drawn. Find the probability that the card drawn will:(v) be a face card of red colour
(v) There are 26 red cards in a deck, and 6 of these cards are face cards (2 kings, 2 queens and 2 jacks). The number of favourable outcomes for the event of drawing a face card of red color = 6...
From a well shuffled deck of 52 cards, one card is drawn. Find the probability that the card drawn will: (i) be a black card. (ii) not be a red card. (iii) be a red card. (iv) be a face card.
(iii) Number of red cards in a deck = 26 The number of favourable outcomes for the event of drawing a red card = 26 Then, probability of drawing a red card = 26/52 = ½ (iv) There are 52 cards...
From a well shuffled deck of 52 cards, one card is drawn. Find the probability that the card drawn will: (i) be a black card. (ii) not be a red card.
Solution: We know that, Total number of cards = 52 So, the total number of outcomes = 52 There are 13 cards of each type. The cards of heart and diamond are red in colour. Spade and diamond are...
In a single throw of a die, find the probability that the number: (iii) will be an odd number.
(iii) If E = event of getting an odd number = {1, 3, 5} So, n(E) = 3 Then, probability of a getting an odd number = n(E)/ n(s) = 3/6 = ½
In a single throw of a die, find the probability that the number: (i) will be an even number. (ii) will not be an even number.
Solution: Here, the sample space = {1, 2, 3, 4, 5, 6} n(s) = 6 (i) If E = event of getting an even number = {2, 4, 6} n(E) = 3 Then, probability of a getting an even number = n(E)/ n(s) = 3/6 = ½...
In a single throw of a die, find the probability of getting a number: (iii) not greater than 4.
(iii) E = event of getting a number not greater than 4 = {1, 2, 3, 4} So, n (E) = 4 Then, probability of getting a number not greater than 4 = n(E)/ n(s) = 4/6 = 2/3
In a single throw of a die, find the probability of getting a number: (i) greater than 4. (ii) less than or equal to 4.
Solution: Here, the sample space = {1, 2, 3, 4, 5, 6} So, n (s) = 6 (i) If E = event of getting a number greater than 4 = {5, 6} So, n (E) = 2 Then, probability of getting a number greater than 4 =...
. A bag contains 3 white, 5 black and 2 red balls, all of the same shape and size. A ball is drawn from the bag without looking into it, find the probability that the ball drawn is:(v) not a black ball
(v) There are 3 + 2 = 5 balls which are not black So, the number of favourable outcomes = 5 Thus, P(getting a white ball) = 5/10 = ½
A bag contains 3 white, 5 black and 2 red balls, all of the same shape and size. A ball is drawn from the bag without looking into it, find the probability that the ball drawn is: (iii) a white ball. (iv) not a red ball.
(iii) There are 3 white balls So, the number of favourable outcomes = 3 Thus, P(getting a white ball) = 3/10 = 3/10 (iv) There are 3 + 5 = 8 balls which are not red So, the number of favourable...
A bag contains 3 white, 5 black and 2 red balls, all of the same shape and size. A ball is drawn from the bag without looking into it, find the probability that the ball drawn is: (i) a black ball. (ii) a red ball
Solution: Total number of balls = 3 + 5 + 2 = 10 So, the total number of possible outcomes = 10 (i) There are 5 black balls So, the number of favourable outcomes = 5 Thus, P(getting a black ball) = ...
A bag contains 3 white, 5 black and 2 red balls, all of the same shape and size. A ball is drawn from the bag without looking into it, find the probability that the ball drawn is: (i) a black ball. (ii) a red ball
Solution: Total number of balls = 3 + 5 + 2 = 10 So, the total number of possible outcomes = 10 (i) There are 5 black balls So, the number of favourable outcomes = 5 Thus, P(getting a black ball) = ...
1. A coin is tossed once. Find the probability of: (i) getting a tail (ii) not getting a tail
Solution: Here, the sample space = {H, T} i.e. n(S) = 2 (i) If A = Event of getting a tail = {T} Then, n(A) = 1 Hence, the probability of getting a tail = n(A)/ n(S) = 1/2 (ii) Not getting a tail As...
A cylindrical water tank of diameter 2.8m and height 4.2m is being fed by a pipe of diameter 7 cm through which water flows at the rate of 4m/s. Calculate, in minutes, the time it takes to fill the tank.
Diameter of cylindrical tank = 2.8 m radius = 1.4 m Height = 4.2 m \[\begin{array}{*{35}{l}} Volume\text{ }of\text{ }water\text{ }filled\text{ }in\text{ }it\text{ }=\text{ }\pi {{r}^{2}}h \\...
The cross-section of a tunnel is a square of side 7 m surmounted by a semicircle as shown in the following figure.The tunnel is 80 m long. Calculate:(iii) its floor area
FIGURE: Side of square (a) = 7m the radius of semi-circle = 7/2 m Length of the tunnel = 80 m \[\begin{array}{*{35}{l}} Area\text{ }of\text{ }cross\text{ }section\text{ }of\text{ }the\text{...
The cross-section of a tunnel is a square of side 7 m surmounted by a semicircle as shown in the following figure.The tunnel is 80 m long. Calculate: (i) its volume (ii) the surface area of the tunnel (excluding the floor)
FIGURE: Side of square (a) = 7m the radius of semi-circle = 7/2 m Length of the tunnel = 80 m \[\begin{array}{*{35}{l}} Area\text{ }of\text{ }cross\text{ }section\text{ }of\text{ }the\text{...
In the following diagram a rectangular platform with a semicircular end on one side is 22 meters long from one end to the other end. If the length of the half circumference is 11 meters, find the cost of constructing the platform, 1.5 meters high at the rate of Rs 4 per cubic meters.
Length of the platform = 22 m Circumference of semi-circle (c) = 11 m \[\begin{array}{*{35}{l}} radius\text{ }=\text{ }\left( c\text{ x }2 \right)/\text{ }\left( 2\text{ x }\pi \right)\text{...
An iron pole consisting of a cylindrical portion 110 cm high and of base diameter 12 cm is surmounted by a cone 9 cm high. Find the mass of the pole, given that 1 cm3 of iron has 8 gm of mass (approx). (Take π = 355/113)
Radius of the base of poles (r) = 6 cm Height of the cylindrical part (h1) = 110 cm Height of the conical part (h2) = 9 cm \[\begin{array}{*{35}{l}} Total\text{ }volume\text{ }of\text{ }the\text{...
Determine the ratio of the volume of a cube to that of a sphere which will exactly fit inside the cube.
Let edge of the cube = a Then, volume of the cube = a x a x a = a3 The sphere that exactly fits in the cube will have radius ‘a/2’ \[\begin{array}{*{35}{l}} Volume\text{ }of\text{ }sphere\text{...
The diameter of a sphere is 6 cm. It is melted and drawn into a wire of diameter 0.2 cm. Find the length of wire.
Diameter of the sphere = 6 cm Radius = 3 cm \[~volume\text{ }=\text{ }4/3\text{ }\pi {{r}^{3~}}=\text{ }4/3\text{ x }22/7\text{ x }3\text{ x }3\text{ x }3\text{ }=\text{ }792/7\text{...
A solid is in the form of a cone standing on a hemisphere with both their radii being equal to 8 cm and the height of cone is equal to its radius. Find in terms of π, the volume of the solid.
Radius of both cone and hemisphere = 8 cm And, height = 8 cm \[\begin{array}{*{35}{l}} Volume\text{ }of\text{ }the\text{ }solid\text{ }=\text{ }Volume\text{ }of\text{ }cone\text{ }+\text{...
A right circular cylinder having diameter 12 cm and height 15 cm is full of ice-cream. The ice-cream is to be filled in identical cones of height 12 cm and diameter 6 cm having a hemi-spherical shape on the top. Find the number of cones required.
Diameter of the cylinder = 12 cm => radius = 6 cm Height of the cylinder = 15 cm Diameter of the cone = 6 cm =>radius = 3 cm Height of the cone = 12 cm Radius of the hemisphere = 3 cm Let the...
A largest sphere is to be carved out of a right circular cylinder of radius 7 cm and height 14 cm. Find the volume of the sphere. (Answer correct to the nearest integer)
Radius of the largest sphere that can be formed inside the cylinder will be equal to the radius of the cylinder. radius of the largest sphere = 7 cm \[\begin{array}{*{35}{l}} Volume\text{ }of\text{...
What is the least number of solid metallic spheres, each of 6 cm diameter, that should be melted and recast to form a solid metal cone whose height is 45 cm and diameter is 12 cm?
Diameter of solid metallic sphere = 6 cm So, its radius = 3 cm Height of solid metal cone = 45 Diameter of metal cone = 12 cm Its radius = 6 cm Let the number of solid metallic spheres be ‘n’...
A wooden toy is in the shape of a cone mounted on a cylinder as shown alongside. If the height of the cone is 24 cm, the total height of the toy is 60 cm and the radius of the base of the cone = twice the radius of the base of the cylinder = 10 cm; find the total surface area of the toy. [Take π = 3.14]
Height of the cone (h) = 24 cm Height of the cylinder (H) = 36 cm Radius of the cone (r) = twice the radius of the cylinder = 10 cm Radius of the cylinder (R) = 5 cm \[\begin{array}{*{35}{l}}...
A vessel is a hollow cylinder fitted with a hemispherical bottom of the same base. The depth of the cylindrical part is 4(2/3) m and the diameter of hemisphere is 3.5 m. Calculate the capacity and the internal surface area of the vessel.
Diameter of the base = 3.5 m So, its radius = 3.5/2 m = 1.75 m = 7/4 m Height of cylindrical part = 4 + 2/3 = 14/3 (i) \[\begin{array}{*{35}{l}} Capacity\text{ }\left( volume \right)\text{ }of\text{...
A cylindrical boiler, 2 m high, is 3.5 m in diameter. It has a hemispherical lid. Find the volume of its interior, including the part covered by the lid.
Diameter of cylindrical boiler = 3.5 m So, the radius (r) = 3.5/2 = 35/20 = 7/4 m Height (h) = 2m Radius of hemisphere (R) = 7/4 m \[\begin{array}{*{35}{l}} Total\text{ }volume\text{ }of\text{...
A circus tent is cylindrical to a height of 8 m surmounted by a conical part. If total height of the tent is 13 m and the diameter of its base is 24 m; calculate: (i) total surface area of the tent (ii) area of canvas, required to make this tent allowing 10% of the canvas used for folds and stitching.
Height of the cylindrical part = H = 8 m Height of the conical part = h = (13 – 8) m = 5 m Diameter = 24 m Its radius \[\begin{array}{*{35}{l}} =\text{ }24/2\text{ }=\text{ }12\text{ }m \\...
A circus tent is cylindrical to a height of 4 m and conical above it. If its diameter is 105 m and its slant height is 80 m, calculate the total area of canvas required. Also, find the total cost of canvas used at Rs 15 per meter if the width is 1.5 m
Radius of the cylindrical part of the tent (r) =105/2 m Slant height (l) = 80 m the total curved surface area of the tent \[\begin{array}{*{35}{l}} =\text{ }2\pi r\text{ }h\text{ }+\text{ }\pi rl ...
From a solid cylinder whose height is 16 cm and radius is 12 cm, a conical cavity of height 8 cm and of base radius 6 cm is hollowed out. Find the volume and total surface area of the remaining solid.
Radius of solid cylinder (R) = 12 cm And, Height (H) = 16 cm \[\begin{array}{*{35}{l}} Volume\text{ }=\text{ }\pi {{R}^{2~}}h\text{ }=\text{ }22/7\text{ }x\text{ }12\text{ }x\text{ }12\text{...
From a solid right circular cylinder with height 10 cm and radius of the base 6 cm, a right circular cone of the same height and same base are removed. Find the volume of the remaining solid.
Height of the cylinder (h) = 10 cm And radius of the base (r) = 6 cm Volume of the cylinder = πr2 h Height of the cone = 10 cm Radius of the base of cone = 6 cm \[\begin{array}{*{35}{l}}...
A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of the top which is open is 5 cm. It is filled with water up to the rim. When lead shots, each of which is a sphere of radius 0.5 cm, are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
Height of cone = 8 cm Radius = 5 cm \[\begin{array}{*{35}{l}} Volume\text{ }=~1/3\text{ }\pi {{r}^{2~}}h \\ =\text{ }1/3\text{ x }22/7\text{ x }5\text{ x }5\text{ x }8\text{ }c{{m}^{3}} \\ =\text{...
The cubical block of side 7 cm is surmounted by a hemisphere of the largest size. Find the surface area of the resulting solid.
Since, the diameter of the largest hemisphere that can be placed on a face of a cube of side 7 cm will be 7 cm. radius = r = 7/2 cm It’s curved surface area = 2 πr2 = 2 x 22/7 x 7/2 x 7/2 = 77...
From a rectangular solid of metal 42 cm by 30 cm by 20 cm, a conical cavity of diameter 14 cm and depth 24 cm is drilled out. Find:(iii) the weight of the material drilled out if it weighs 7 gm per cm3.
\[\left( iii \right)\text{ }Weight\text{ }of\text{ }material\text{ }drilled\text{ }out\text{ }=\text{ }1232\text{ x }7g\text{ }=\text{ }8624g\text{ }=\text{ }8.624\text{ }kg\]
From a rectangular solid of metal 42 cm by 30 cm by 20 cm, a conical cavity of diameter 14 cm and depth 24 cm is drilled out. Find: (i) the surface area of the remaining solid (ii)the volume of remaining solid
Dimensions of rectangular solid l = 42 cm, b = 30 cm and h = 20 cm Conical cavity’s diameter = 14 cm its radius = 7 cm Depth (height) = 24 cm (i) Total surface area of cuboid...
A buoy is made in the form of a hemisphere surmounted by a right cone whose circular base coincides with the plane surface of the hemisphere. The radius of the base of the cone is 3.5 m and its volume is two-third of the hemisphere. Calculate the height of the cone and the surface area of the buoy, correct to two decimal places.
Radius of the hemisphere part (r) = 3.5 m = 7/2 m Volume of hemisphere \[\begin{array}{*{35}{l}} =\text{ }2/3\text{ }\pi {{r}^{3}} \\ =\text{ }2/3\text{ x }22/7\text{ x }7/2x\text{ }7/2\text{ x...
A cone of height 15 cm and diameter 7 cm is mounted on a hemisphere of same diameter. Determine the volume of the solid thus formed.
Height of the cone = 15 cm Diameter of the cone = 7 cm its radius = 3.5 cm Radius of the hemisphere = 3.5 cm Volume of the solid = Volume of the cone + Volume of the hemisphere...
A hemi-spherical bowl of internal radius 9 cm is full of liquid. This liquid is to be filled into conical shaped small containers each of diameter 3 cm and height 4 cm. How many containers are necessary to empty the bowl?
Radius of hemispherical bowl = 9 cm \[Volume\text{ }=\text{ }2/3\text{ }\pi {{r}^{3}}~=\text{ }2/3\text{ }\pi {{9}^{3}}~=\text{ }2/3\text{ }\pi \text{ }x\text{ }729\text{ }=\text{ }486\text{ }\pi...
A solid rectangular block of metal 49 cm by 44 cm by 18 cm is melted and formed into a solid sphere. Calculate the radius of the sphere.
Volume of rectangular block \[=\text{ }49\text{ x }44\text{ x }18\text{ }c{{m}^{3}}~=\text{ }38808\text{ }c{{m}^{3}}~\ldots \ldots \text{ }\left( i \right)\] Let r be the radius of sphere....
Total volume of three identical cones is the same as that of a bigger cone whose height is 9 cm and diameter 40 cm. Find the radius of the base of each smaller cone, if height of each is 108 cm.
Let the radius of the smaller cone be r cm Diameter of bigger cone = 40 cm the radius = 20 cm and height = 9 cm \[\begin{array}{*{35}{l}} Volume\text{ }of\text{ }larger\text{ }cone\text{ }=\text{...
The radii of the internal and external surfaces of a metallic spherical shell are 3 cm and 5 cm respectively. It is melted and recast into a solid right circular cone of height 32 cm. find the diameter of the base of the cone.
Height of the solid right circular cone = 32 cm Internal radius metallic spherical shell = 3 cm External radius spherical shell = 5 cm the volume of the spherical shell \[\begin{array}{*{35}{l}}...
A hollow sphere of internal and external diameters 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. Find the height of the cone.
External diameter of the hollow sphere = 8 cm radius (R) = 4 cm Internal diameter of the hollow sphere = 4 cm radius (r) = 2 cm Then, the volume of metal used in hollow sphere = Also given, Diameter...
A solid sphere of radius 15 cm is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate the number of cones recast.
Radius of the sphere = R = 15 cm So, the volume of sphere melted \[=\text{ }4/3\text{ }\pi {{R}^{2}}~=\text{ }4/3\text{ x }\pi \text{ x }15\text{ x }15\text{ x }15\] Radius of each cone recasted = r...
The volume of one sphere is 27 times that of another sphere. Calculate the ratio of their: (i) radii (ii) surface areas
The volume of first sphere = 27 x volume of second sphere Let the radius of the first sphere = r1 and, radius of second sphere = r2 (i) Then, according to the question we have...
8 metallic sphere; each of radius 2 mm, are melted and cast into a single sphere. Calculate the radius of the new sphere.
Radius of metallic sphere = 2mm = 1/5 cm \[\begin{array}{*{35}{l}} Volume\text{ }=\text{ }4/3\text{ }\pi {{r}^{3}}~=\text{ }4/3\text{ x }22/7\text{ x }1/5\text{ x }1/5\text{ x }1/5\text{ }=\text{...
How many balls each of radius 1 cm can be made by melting a bigger ball whose diameter is 8 cm.
Diameter of bigger ball = 8 cm radius of bigger ball = 4 cm \[Volume\text{ }=\text{ }4/3\text{ }\pi {{r}^{3}}~=\text{ }4/3\text{ }\pi \text{ }{{4}^{3}}~=\text{ }265\pi /3\text{ }c{{m}^{3}}\] Radius...
A spherical ball of lead has been melted and made into identical smaller balls with radius equal to half the radius of the original one. How many such balls can be made?
Let the radius of the spherical ball = r the volume = 4/3 πr3 And, the radius of smaller ball = r/2 Volume of smaller ball \[=\text{ }4/3\text{ }\pi {{\left( r/2 \right)}^{3}}~=\text{ }4/3\text{...
The volume of a sphere is 38808 cm3; find its diameter and the surface area.
Volume of the sphere = 38808 cm3 Let the radius of the sphere \[\begin{array}{*{35}{l}} =\text{ }r \\ 4/3\text{ }\pi {{r}^{3}}~=\text{ }38808 \\ 4/3\text{ x }\left( 22/7 \right)\text{ x...
The surface area of a sphere is 2464 cm2, find its volume.
Surface area of the sphere = 2464 cm2 Let the radius of the sphere be r. surface area of the sphere \[\begin{array}{*{35}{l}} =\text{ }4\pi {{r}^{2}} \\ 4\pi {{r}^{2}}~=\text{ }2464 \\ 4\text{ x...
There are two cones. The curved surface area of one is twice that of the other. The slant height of the latter is twice that of the former. Find the ratio of their radii.
Let slant height of the first cone = l So, the slant height of the second cone = 2l Radius of the first cone = r1 And, the radius of the second cone = r2 Curved surface area of first cone = πr1l...
The diameters of two cones are equal. If their slant heights are in the ratio 5:4, find the ratio of their curved surface areas.
Let radius of each cone = r Given that, ratio between their slant heights = 5: 4 Let slant height of the first cone = 5x And slant height of second cone = 4x So, curved surface area of the first...
Two right circular cones x and y are made, x having three times the radius of y and y having half the volume of x. Calculate the ratio between the heights of x and y.
Let radius of cone y = r radius of cone x = 3r volume of cone y = V Then, volume of cone x = 2V Let h1 be the height of x and h2 be the height of y. \[\begin{array}{*{35}{l}} Volume\text{ }of\text{...
The radius and height of a right circular cone are in the ratio 5:12 and its volume is 2512 cubic cm. Find the radius and slant height of the cone. (Take π = 3.14)
The ratio between radius and height = 5: 12 Volume of the right circular cone = 2512 cm3 Let its radius (r) = 5x, its height (h) = 12x and slant height = l \[\begin{array}{*{35}{l}}...
The circumference of the base of a 12 m high conical tent is 66 m. Find the volume of the air contained in it.
Circumference of the base (c) = 66 m Height of the conical tent (h) = 12 m Radius \[=\text{ }c/2\pi \text{ }=\text{ }66/\text{ }2\pi \text{ }=\text{ }\left( 33\text{ x }7 \right)/22\text{ }=\text{...
The curved surface area of a cone is 12320 cm2. If the radius of its base is 56 cm, find its height.
Curved surface area of the cone = 12320 cm2 Radius of the base = 56 cm Let the slant height be ‘l’ Curved surface area \[\begin{array}{*{35}{l}} =\text{ }\pi rl\text{ }=\text{ }12320\text{...
Find the volume of a cone whose slant height is 17 cm and radius of base is 8 cm.
Slant height of the cone (l) = 17 cm Base radius (r) \[\begin{array}{*{35}{l}} =\text{ }8\text{ }cm \\ {{l}^{2}}~=\text{ }{{r}^{2}}~+\text{ }{{h}^{2}} \\ {{h}^{2}}~=\text{ }{{l}^{2}}~-\text{...
Find the minimum length in cm and correct to nearest whole number of the thin metal sheet required to make a hollow and closed cylindrical box of diameter 20 cm and height 35 cm. Given that the width of the metal sheet is 1 m. Also, find the cost of the sheet at the rate of Rs. 56 per m. Find the area of metal sheet required, if 10% of it is wasted in cutting, overlapping, etc.
Height of the cylinder box = h = 35 cm Base radius of the cylinder box = r = 10 cm Width of metal sheet = 1m = 100 cm Area of metal sheet required = total surface area of the box Length x width =...
The radius of a solid right circular cylinder decreases by 20% and its height increases by 10%. Find the percentage change in its: (i) volume (ii) curved surface area
Let the original dimensions of the solid right cylinder be radius (r) and height (h) in cm. Then its volume = πr2h cm3and curved surface area = 2πrh Now, after the changes the new dimensions are:...
The radius of a solid right circular cylinder increases by 20% and its height decreases by 20%. Find the percentage change in its volume.
The radius of a solid right cylinder (r) = 100 cm let the height of a solid right circular cylinder (h) = 100 cm The volume (original) of a solid right circular cylinder \[\begin{array}{*{35}{l}}...
The height and the radius of the base of a cylinder are in the ratio 3:1. If its volume is 1029π cm3; find its total surface area.
The ratio between height and radius of a cylinder = 3:1 Volume = 1029π cm3 …….(i) the radius of the base = r Then, it’s height will be = 3r Volume \[\begin{array}{*{35}{l}} =\text{ }\pi...
Find the total surface area of an open pipe of length 50 cm, external diameter 20 cm and internal diameter 6 cm.
Length of the open pipe = 50 cm Its external diameter = 20 cm It’s external radius (R) = 10 cm Its internal diameter = 6 cm => It’s internal radius (r) = 3 cm Surface area of pipe open from both...
A cylindrical container with internal radius of its base 10 cm, contains water up to a height of 7 cm. Find the area of wetted surface of the cylinder.
Internal radius of the cylindrical container = 10 cm = r Height of water = 7 cm = h So, the surface area of the wetted surface \[\begin{array}{*{35}{l}} =\text{ }2\pi rh\text{ }+\text{ }\pi...
A cylindrical container with diameter of base 42 cm contains sufficient water to submerge a rectangular solid of iron with dimensions 22 cm x 14 cm x 10.5 cm. Find the rise in level of the water when the solid is submerged.
Diameter of cylindrical container = 42 cm it’s radius (r) = 21 cm Dimensions of rectangular solid = 22cm x 14cm x 10.5cm The volume of solid = 22 x 14 x 10.5 cm3 ….. (i) Let the height of water = h...
A metal pipe has a bore (inner diameter) of 5 cm. The pipe is 5 mm thick all round. Find the weight, in kilogram, of 2 metres of the pipe if 1 cm3 of the metal weights 7.7 g.
Inner radius of the pipe = r = 5/2 = 2.5 cm External radius of the pipe = R = Inner radius of the pipe + Thickness of the pipe \[=\text{ }2.5\text{ }cm\text{ }+\text{ }0.5\text{ }cm\text{ }=\text{...
A cylinder has a diameter of 20 cm. The area of curved surface is 100 sq cm. Find: (i) the height of the cylinder correct to one decimal place. (ii) the volume of the cylinder correct to one decimal place.
The diameter of the cylinder = 20 cm the radius (r) = 10 cm and the curved surface area = 100 cm2 Height = h cm (i) Curved surface area \[\begin{array}{*{35}{l}} =\text{ }2\pi rh \\ 2\pi rh\text{...
What length of solid cylinder 2 cm in diameter must be taken to recast into a hollow cylinder of external diameter 20 cm, 0.25 cm thick and 15 cm long?
External diameter of hollow cylinder = 20 cm So, it’s radius = 10 cm = R Thickness = 0.25 cm the internal radius \[=\text{ }\left( 10\text{ }-\text{ }0.25 \right)\text{ }=\text{ }9.75\text{...
How many cubic meters of earth must be dug out to make a well 28 m deep and 2.8 m in diameter? Also, find the cost of plastering its inner surface at Rs 4.50 per sq meter.
Radius of the well = 2.8/2 = 1.4 m Depth of the well = 28 m Hence, the volume of earth dug out \[\begin{array}{*{35}{l}} =~\pi {{r}^{2}}h \\ =\text{ }\left( 22/7 \right)\text{ x }1.4\text{ x...
A cylinder of circumference 8 cm and length 21 cm rolls without sliding for 4½ seconds at the rate of 9 complete rounds per second. Find: (i) distance travelled by the cylinder in 4½ seconds, and (ii) the area covered by the cylinder in 4½ seconds
Base circumference of cylinder (c) = 8 cm So, the radius \[=\text{ }c/2\pi \text{ }=\text{ }\left( 8\text{ x }7 \right)/\text{ }\left( 2\text{ x }22 \right)\text{ }=\text{ }14/11\text{ }cm\] Length...
The inner radius of a pipe is 2.1 cm. How much water can 12 m of this pipe hold?
The inner radius of the pipe = 2.1 cm Length of the pipe = 12 m = 1200 cm Volume of the pipe \[\begin{array}{*{35}{l}} =\text{ }\pi {{r}^{2}}h\text{ }=\text{ }22/7\text{ x }{{2.1}^{2}}~x\text{...
The height of a circular cylinder is 20 cm and the radius of its base is 7 cm. Find: (i) the volume (ii) the total surface area.
Since, a circular cylinder whose Height, h = 20 cm and base radius, r = 7 cm (i) Volume of cylinder \[\begin{array}{*{35}{l}} =\text{ }\pi {{r}^{2}}h\text{ }=\text{ }22/7\text{ }x\text{...
Construct a circle, inscribing an equilateral triangle with side 5.6 cm.
Steps for Construction: i) Draw a line segment BC = 5.6 cm ii) With centres B and C, draw two arcs of 5.6 cm radius each which intersect each other at A. iii) And, join AB and AC. iv) Draw angle...
Construct an equilateral triangle ABC with side 6 cm. Draw a circle circumscribing the triangle ABC.
Steps for construction: i) Draw a line segment BC = 6 cm ii) Draw two arcs of radius 6 cm with centres B and C, which intersect each other at A. iii) Then, join AC and AB. iv) Draw perpendicular...
i) Using ruler and compasses only, construct a triangle ABC in which AB = 8 cm, BC = 6 cm and CA = 5 cm. ii) Find its incentre and mark it I.iii) With I as centre, draw a circle which will cut off 2 cm chords from each side of the triangle.
Steps for construction: i) Draw a line segment BC = 6 cm. ii) Draw an arc with centre B and radius 8 cm. iii) Draw another arc with centre C and radius 5 cm which intersects the first arc at A. iv)...
The bisectors of angles A and B of a scalene triangle ABC meet at O. iii) What is the relation between angle ACO and angle BCO?
iii) OC is the bisector of angle C Thus, ∠ACO = ∠BCO
The bisectors of angles A and B of a scalene triangle ABC meet at O. i) What is the point O called? ii) OR and OQ are drawn perpendiculars to AB and CA respectively. What is the relation between OR and OQ?
i) O is called the incentre of the incircle of ΔABC. ii) OR and OQ are the radii of the incircle and OR = OQ.
Perpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.(iii) Does the perpendicular bisector of BC pass through O?
iii) Yes, the perpendicular bisector of BC will pass through O.
Perpendicular bisectors of the sides AB and AC of a triangle ABC meet at O. (i) What do you call the point O? (ii) What is the relation between the distances OA, OB and OC?
i) O is called the circumcentre of circumcircle of ΔABC. ii) OA, OB and OC are the radii of the circumcircle.
Using ruler and compasses only construct a triangle ABC in which BC = 4 cm, ∠ACB = 45o and perpendicular from A on BC is 2.5 cm. Draw a circle circumscribing the triangle ABC.
Steps for Construction: i) Draw a line segment BC = 4 cm. ii) At C, draw a perpendicular line CX and from it, cut off CE = 2.5 cm. iii) Draw another perpendicular line EY from E. iv) From C, draw a...
Using ruler and compasses only, (i) Construct a triangle ABC with the following data: Base AB = 6 cm, BC = 6.2 cm and ∠CAB = 60o (ii) In the same diagram, draw a circle which passes through the points A, B and C and mark its centre as O. (iii) Draw a perpendicular from O to AB which meets AB in D. (iv) Prove that AD = BD
Steps for construction: i) Draw a line segment AB = 6 cm ii) Draw a ray at A, making an angle of 60o with BC. iii) With B as centre and radius = 6.2 cm draw an arc which intersects AX ray at C. iv)...
Using ruler and compasses only, draw an equilateral triangle of side 5 cm. Draw its inscribed circle. Measure the radius of the circle.
Steps for Construction: i) Draw a line segment BC = 5 cm ii) With centres as B and C, draw two arcs of radius 5 cm each which intersect each other at A. iii) Then, join AB and AC. iv) Draw angle...
Using ruler and compasses only. (i) Construct triangle ABC, having given BC = 7 cm, AB-AC = 1 cm and ∠ABC = 45o. (ii) Inscribe a circle in the ΔABC constructed in (i) above.
Steps for construction: A. Construction of triangle: a) Draw a line segment BC = 7 cm b) At B, draw a ray BX making an angle of 45o and cut off BE = AB – AC = 1 cm c) Join EC and draw the...
Using ruler and compasses only, draw an equilateral triangle of side 4.5 cm and draw its circumscribed circle. Measure the radius of the circle.
Steps for construction: i) Draw a line segment BC = 4.5 cm ii) With centres B and C, draw two arcs of radius 4.5 cm which intersect each other at A. iii) And join AC and AB. iv) Draw the...
Draw a circle of radius 4.5 cm. Draw two tangents to this circle so that the angle between the tangents is 60º.
Steps for Construction: i) draw a circle with centre O, with radius BC = 4.5 cm ii) Draw arcs making an angle of 180º – 60º = 120º at O such that ∠AOB = 120º iii) At A and B, draw two rays making...
Draw a circle of radius 5 cm. Draw two tangents to this circle so that the angle between the tangents is 45º.
Steps for construction: i) draw a circle with centre O,with radius BC = 5 cm ii) Draw arcs making an angle of 180º – 45º = 135º at O such that ∠AOB = 135º iii) At A and B, draw two rays making an...
Draw a circle of diameter of 9 cm. Mark a point at a distance of 7.5 cm from the centre of the circle. Draw tangents to the given circle from this exterior point. Measure the length of each tangent.
Steps for construction: i) Taking O as the centre, draw a circle of diameter 9 cm (radius = 4.5 cm). ii) Mark a point P outside the circle, such that PO = 7.5 cm. iii) Taking OP as the diameter,...
Draw a circle of radius 3 cm. Mark a point P at a distance of 5 cm from the centre of the circle drawn. Draw two tangents PA and PB to the given circle and measure the length of each tangent.
Steps for construction: i) Draw a circle with centre O and radius 3 cm. ii) Take a point P from O, such that OP = 5 cm. iii) Now, draw a bisector of OP which intersects OP at M. iv) With centre M,...
AB is diameter and AC is a chord of a circle with centre O such that angle BAC=30º. The tangent to the circle at C intersects AB produced in D. Show that BC = BD.
Join \[OC\] \[\angle BCD\text{ }=\angle BAC\text{ }=\] \[{{30}^{o}}~\] [Angles in the alternate segment] It’s seen that, arc \[BC\]subtends \[\angle DOC\]at the center of the circle And \[\angle...
If PQ is a tangent to the circle at R; calculate: i) ∠PRS ii) ∠ROT When O is the centre of the circle and ∠TRQ = 30degree
Solution: (i) As \[PQ\] is the tangent and \[OR\]is the radius. So, \[OR\bot PQ\] \[\angle ORT\text{ }=\text{ }{{90}^{o}}\] \[\angle TRQ\text{ }=\text{ }{{90}^{o}}-\text{ }{{30}^{o}}~=\text{...
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ADB = 30degree and ∠CBD = 60degree; calculate: ∠CDB
Solution: As \[BD\] is the diameter, we have \[\angle BCD\text{ }=\text{ }{{90}^{o}}\] [Angle in a semi-circle] Now in \[\vartriangle BCD\] \[\angle CDB\text{ }+\angle CBD\text{ }+\angle BCD\text{...
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ADB = 30degree and ∠CBD = 60degree; calculate: i) ∠QAB ii) ∠PAD
Solution: (i) Given, \[PAQ\]is a tangent and \[AB\]is the chord \[\angle QAB~=\angle ADB\text{ }=\text{ }{{30}^{o}}~\] [Angles in the alternate segment] (ii) \[OA\text{ }=\text{ }OD\][radii of the...
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find (i) AB. (ii) the length of tangent PT.
Solution: (i) \[PA\text{ }=\text{ }AB\text{ }+\text{ }BP\text{ }=\text{ }\left( AB\text{ }+\text{ }4 \right)\text{ }cm\] \[PC\text{ }=\text{ }PD\text{ }+\text{ }CD\] \[=\text{ }5\text{ }+\text{...
In the given figure, tangent PT = 12.5 cm and PA = 10 cm; find AB.
Solution: As \[PAB\]is the secant and \[PT\]is the tangent, we have \[P{{T}^{2}}~=\text{ }PA\text{ }x\text{ }PB\] \[{{12.5}^{2}}~=\text{ }10\text{ }x\text{ }PB\] \[PB\text{ }=\text{ }\left(...
