Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
If the points
If 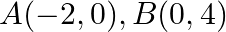 and
and 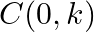 be three points such that area of a
be three points such that area of a  is 4 sq units, find the value of
is 4 sq units, find the value of  .
.
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the value of  for which the area of a ABC having vertices
for which the area of a ABC having vertices 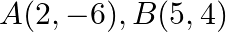 and
and 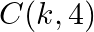 is 35 sq units.
is 35 sq units.
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the value of  for which the points
for which the points 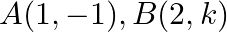 and
and 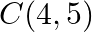 are collinear.
are collinear.
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the value of  for which the points
for which the points 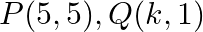 and
and 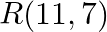 are collinear.
are collinear.
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the value of  for which the points
for which the points 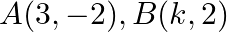 and
and 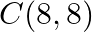 are collinear.
are collinear.
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Use determinants to show that the following points are collinear. 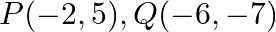 and
and 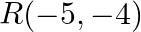
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Use determinants to show that the following points are collinear. 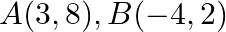 and
and 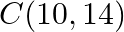
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Use determinants to show that the following points are collinear. 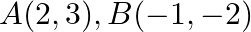 and
and 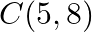
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the area of the triangle whose vertices are: 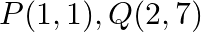 and
and 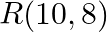
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the area of the triangle whose vertices are: 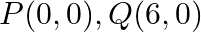 and
and 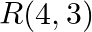
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the area of the triangle whose vertices are: 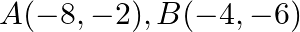 and
and 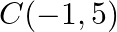
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the area of the triangle whose vertices are: 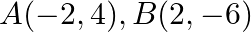 and
and 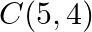
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the area of the triangle whose vertices are: 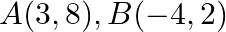 and
and 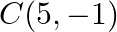
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
A girl goes to her friend’s house, which is at a distance of 12 km. She covers half of the distance at a speed of x km/hr and the remaining distance at a speed of (x + 2) km/hr. If she takes 2 hrs 30 minutes to cover the whole distance, find ‘x’.
Given, The young lady covers a distance of 6 km at a speed x km/hr. Along these lines, the time taken to cover initial 6 km \[=\text{ }6/x\text{ }hr\] [Since, Time = Distance/Speed] Likewise given,...
A car covers a distance of 400 km at a certain speed. Had the speed been 12 km/h more, the time taken for the journey would have been 1 hour 40 minutes less. Find the original speed of the car.
We should accept x km/h to be the first speed of the vehicle. We realize that, Time = Distance/Speed From the inquiry, The time taken by the vehicle to finish 400 km = \[400/x\text{ }hrs\]...
If the speed of an aeroplane is reduced by 40 km/hr, it takes 20 minutes more to cover 1200 km. Find the speed of the aeroplane.
How about we think about the first speed of the plane to be x km/hr. Presently, the time taken to cover a distance of \[1200\text{ }km\text{ }=\text{ }1200/x\text{ }hrs\] [Since, Time =...
The speed of an ordinary train is x km per hr and that of an express train is (x + 25) km per hr. (i) Find the time taken by each train to cover 300 km. (ii) If the ordinary train takes 2 hrs more than the express train; calculate speed of the express train.
(i) Given, Speed of the conventional train \[=\text{ }x\text{ }km/hr\] Speed of the express train \[=\text{ }\left( x\text{ }+\text{ }25 \right)\text{ }km/hr\] Distance \[=\text{ }300\text{ }km\] We...
