Solution: Option(C) To find: Area of $A B C$ Given: $A(3,-2), B(k, 2)$ and $C(8,8)$ The formula used: $\Delta=\frac{1}{2}\left|\begin{array}{lll}x_{1} & y_{1} & 1 \\ x_{2} & y_{2} &...
Mark the tick against the correct answer in the following: If the points
Mark the tick against the correct answer in the following: The vertices of a a 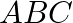 are
are 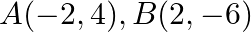 and
and  The area of a
The area of a  is
is
A. 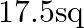 units
units
B. 35 sq units
C. 32 sq units
D. 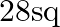 units
units
Solution: Option(B) To find: Area of $A B C$ Given: $A(-2,4), B(2,-6)$ and $C(5,4)$ Formula used: $\Delta=\frac{1}{2}\left|\begin{array}{lll}x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1 \\...
Mark the tick against the correct answer in the following: The solution set of the equation 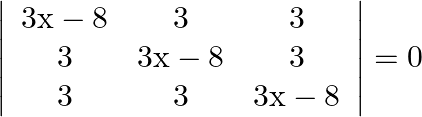 is
is
A. 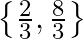
B. 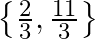
C. 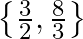
D. None of these
Solution: Option(B) To find: Value of $x$ We have, $\left|\begin{array}{ccc}3 x-8 & 3 & 3 \\ 3 & 3 x-8 & 3 \\ 3 & 3 & 3 x-8\end{array}\right|=0$ Applying $\mathrm{R}_{1}...
Mark the tick against the correct answer in the following: The solution set of the equation 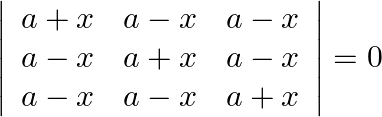 is
is
A. 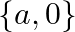
B. 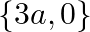
C. 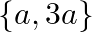
D. None of these
Solution: Option(B) To find: Value of $x$ We have, $\left|\begin{array}{ccc}a+x & a-x & a-x \\ a-x & a+x & a-x \\ a-x & a-x & a+x\end{array}\right|=0$ Applying...
Mark the tick against the correct answer in the following: The solution set of the equation 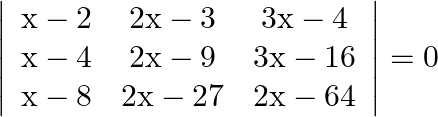 is
is
A. 
B. 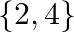
C. 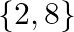
D. 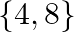
Solution: Option(A) To find: Value of $x$ We have, $\left|\begin{array}{ccc}x-2 & 2 x-3 & 3 x-4 \\ x-4 & 2 x-9 & 3 x-16 \\ x-8 & 2 x-27 & 3 x-64\end{array}\right|=0$ Applying...
Mark the tick against the correct answer in the following: The solution set of the equation 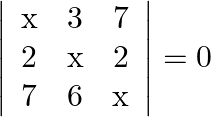 is
is
A. 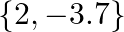
B. 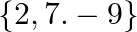
C. 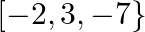
D. none of these
Solution: Option(C) To find: Value of $x$ We have, $\left|\begin{array}{lll}\mathrm{x} & 3 & 7 \\ 2 & \mathrm{X} & 2 \\ 7 & 6 & \mathrm{x}\end{array}\right|=0$ Applying...
Mark the tick against the correct answer in the following: If 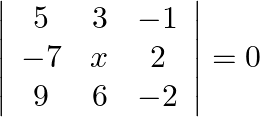 then
then 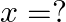
A. 0
B. 6
C. 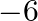
D. 9
Solution: Option(C) To find: Value of $\mathrm{x}$ We have, $\left|\begin{array}{ccc}5 & 3 & -1 \\ -7 & x & 2 \\ 9 & 6 & -2\end{array}\right|=0$ Applying $R_{1} \rightarrow 2...
Mark the tick against the correct answer in the following: 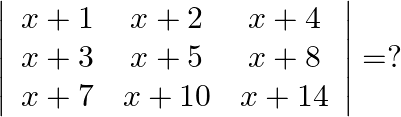
A. 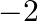
B. 2
C. 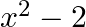
D. 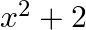
Solution: Option(A) To find: Value of $\left|\begin{array}{ccc}\mathrm{x}+1 & \mathrm{x}+2 & \mathrm{x}+4 \\ \mathrm{x}+3 & \mathrm{x}+5 & \mathrm{x}+8 \\ \mathrm{x}+7 &...
Mark the tick against the correct answer in the following: 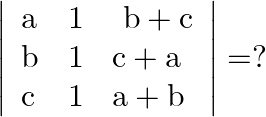
A. 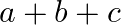
B. 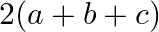
C. 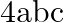
D. 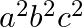
Solution: Option(C) To find: Value of $\left|\begin{array}{lll}a & 1 & b+c \\ b & 1 & c+a \\ c & 1 & a+b\end{array}\right|$ We have, $\left|\begin{array}{lll}a & 1 &...
Mark the tick against the correct answer in the following: 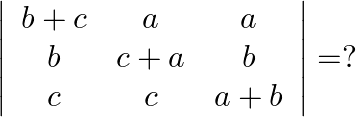
A. 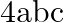
B. 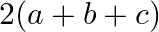
C. 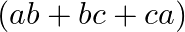
D. none of these
Solution: Option(A) To find: Value of $\left|\begin{array}{ccc}b+c & a & a \\ b & c+a & b \\ c & c & a+b\end{array}\right|$ We have, $\left|\begin{array}{ccc}b+c & a...
Mark the tick against the correct answer in the following: 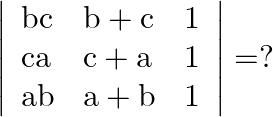
A. 
B. 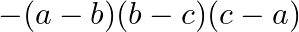
C. 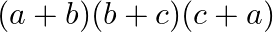
D. None of these
Solution: Option(A) To find: Value of $\left|\begin{array}{lll}\mathrm{bc} & \mathrm{b}+\mathrm{c} & 1 \\ \mathrm{ca} & \mathrm{a}+\mathrm{c} & 1 \\ \mathrm{ab} &...
Mark the tick against the correct answer in the following: 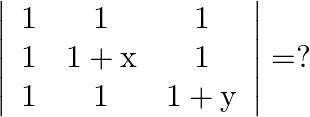
A. 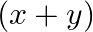
B. 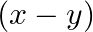
C. 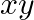
D. none of these
Solution: Option(C) To find: Value of $\left|\begin{array}{ccc}1 & 1 & 1 \\ 1 & 1+x & 1 \\ 1 & 1 & 1+y\end{array}\right|$ We have, $\left|\begin{array}{ccc}1 & 1 & 1...
Mark the tick against the correct answer in the following: 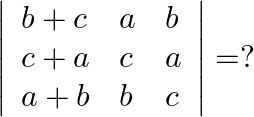
A. 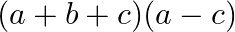
B. 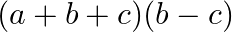
C. 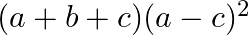
D. 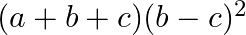
Solution: Option(C) To find: Value of $\left|\begin{array}{lll}b+c & a & b \\ c+a & c & a \\ a+b & b & c\end{array}\right|$ We have,...
Mark the tick against the correct answer in the following: 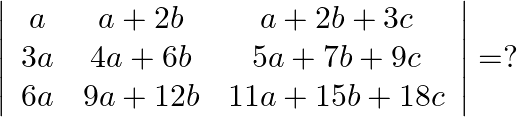
A. 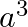
B. 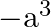
C. 0
D. none of these
Solution: Option(B) To find: Value of $\left|\begin{array}{ccc}a & a+2 b & a+2 b+3 c \\ 3 a & 4 a+6 b & 5 a+7 b+9 c \\ 6 a & 9 a+12 b & 11 a+15 b+18 c\end{array}\right|$ We...
Mark the tick against the correct answer in the following: 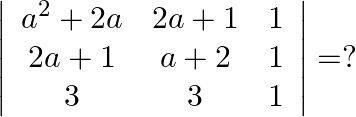
A. 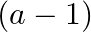
B. 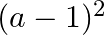
C. 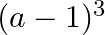
D. none of these
Solution: Option(C) To find: Value of $\left|\begin{array}{ccc}a^{2}+2 a & 2 a+1 & 1 \\ 2 a+1 & a+2 & 1 \\ 3 & 3 & 1\end{array}\right|$ We have,...
Mark the tick against the correct answer in the following: 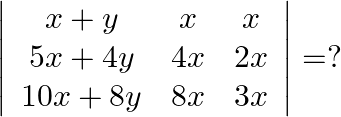
A. 0
B. 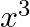
C. 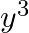
D. none of these
Solution: Option( B) To find: Value of $\left|\begin{array}{ccc}x+y & x & x \\ 5 x+4 y & 4 x & 2 x \\ 10 x+8 y & 8 x & 3 x\end{array}\right|$ We have,...
Mark the tick against the correct answer in the following: If 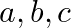 be distinct positive real numbers then the value of
be distinct positive real numbers then the value of 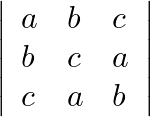 is
is
A. positive
B. negative
C. a perfect square
D. 0
Solution: Option(B) To find: Nature of $\left|\begin{array}{lll}a & b & c \\ b & c & a \\ c & a & b\end{array}\right|$ We have, $\left|\begin{array}{lll}a & b & c \\...
Mark the tick against the correct answer in the following: 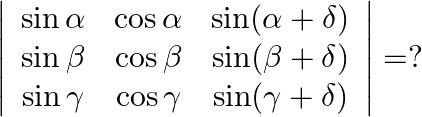
A. 0
B. 1
C. 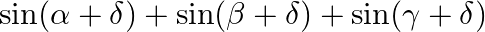
D. none of these
Solution: Option(A) To find: Value of $\left|\begin{array}{lll}\operatorname{sind} & \cos \alpha & \sin (\alpha+\bar{\delta}) \\ \sin \beta & \cos \beta & \sin (\beta+\bar{\delta})...
Mark the tick against the correct answer in the following: 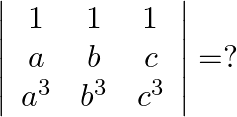
A. 
B. 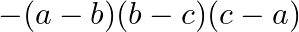
C. 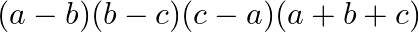
D. 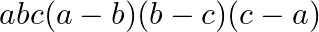
Solution: Option(C) To find: Value of $\left|\begin{array}{ccc}1 & 1 & 1 \\ a & b & c \\ a^{3} & b^{3} & c^{3}\end{array}\right|$ We have, $\left|\begin{array}{ccc}1 & 1...
Mark the tick against the correct answer in the following: 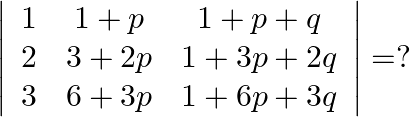
A. 0
B. 1
C. 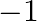
D. none of these
Solution: Option(B) To find: Value of $\left|\begin{array}{ccc}1 & 1+p & 1+p+q \\ 2 & 3+2 p & 1+3 p+2 q \\ 3 & 6+3 p & 1+6 p+3 q\end{array}\right|$ We have,...
Mark the tick against the correct answer in the following: 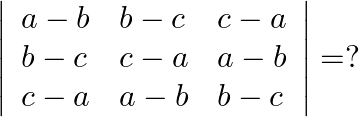
A. 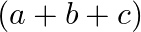
B. 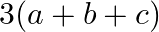
C. 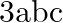
D. 0
Solution: Option(D) To find: Value of $\left|\begin{array}{lll}a-b & b-c & c-a \\ b-c & c-a & a-b \\ c-a & a-b & b-c\end{array}\right|$ We have, $\left|\begin{array}{lll}a-b...
Mark the tick against the correct answer in the following: 
A. 2
B. 6
C. 24
D. 120
Solution: Option(24) To find: Value of $\left|\begin{array}{lll}1 ! & 2 ! & 3 ! \\ 2 ! & 3 ! & 4 ! \\ 3 ! & 4 ! & 5 !\end{array}\right|$ We have,...
Mark the tick against the correct answer in the following: 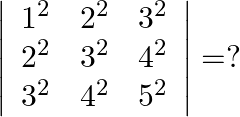
A. 8
B. 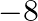
C. 16
D. 142
Solution: Option(A) To find: Value of $\left|\begin{array}{lll}1^{2} & 2^{2} & 3^{2} \\ 2^{2} & 3^{2} & 4^{2} \\ 3^{2} & 4^{2} & 5^{2}\end{array}\right|$ We have,...
Mark the tick against the correct answer in the following: If 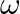 is a complex cube root of unity then the value of
is a complex cube root of unity then the value of  is
is
A. 2
B. 4
C. 0
D. 
Solution: Option(0) To find: Value of $\left|\begin{array}{ccc}1 & \omega & 1+\omega \\ 1+\omega & 1 & \omega \\ \omega & 1+\omega & 1\end{array}\right|$ Formula used: (i)...
Mark the tick against the correct answer in the following: If  is a complex root of unity then
is a complex root of unity then 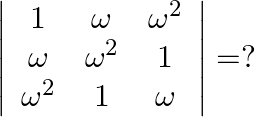
A. 1
B. 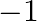
C. 0
D. none of these
Solution: Option(C) To find: Value of $\left|\begin{array}{ccc}1 & \omega & \omega^{2} \\ \omega & \omega^{2} & 1 \\ \omega^{2} & 1 & \omega\end{array}\right|$ We have,...
Mark the tick against the correct answer in the following: 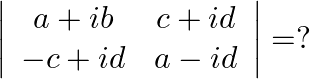
A. 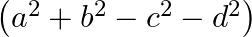
B. 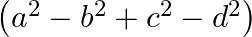
C. 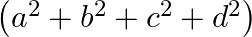
D. none of these
Solution: Option(C) To find: Value of $\left|\begin{array}{cc}a+i b & c+i d \\ -c+i d & a-i b\end{array}\right|$ Formula used: $\mathrm{i}^{2}=-1$ We have, $\left|\begin{array}{cc}a+i b...
Mark the tick against the correct answer in the following: 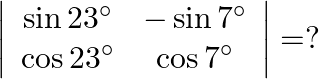
A. 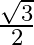
B. 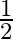
C. 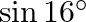
D. 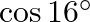
Solution: Option(B) To find: Value of $\left|\begin{array}{cc}\sin 23^{\circ} & -\sin 7^{\circ} \\ \cos 23^{\circ} & \cos 7^{\circ}\end{array}\right|$ Formula used: (i) $\sin (A+B)=\sin A...
Mark the tick against the correct answer in the following: 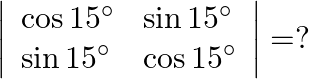
A. 1
B. 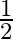
C. 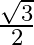
D. none of these
Solution: Option(C) To find: Value of $\left|\begin{array}{ll}\cos 15^{\circ} & \sin 15^{\circ} \\ \sin 15^{\circ} & \cos 15^{\circ}\end{array}\right|$ Formula used: (i) $\cos (A+B)=\cos A...
Mark the tick against the correct answer in the following: 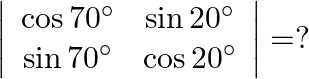
A. 1
B. 0
C. 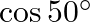
8D. 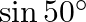
Solution: Option(B) To find: Value of $\left|\begin{array}{cc}\cos 70^{\circ} & \sin 20^{\circ} \\ \sin 70^{\circ} & \cos 20^{\circ}\end{array}\right|$ Formula used: (i) $\cos \theta=\sin...
If the points 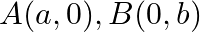 and
and 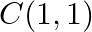 are collinear, prove that
are collinear, prove that 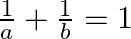
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
If 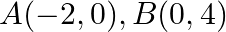 and
and 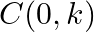 be three points such that area of a
be three points such that area of a 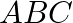 is 4 sq units, find the value of
is 4 sq units, find the value of  .
.
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the value of  for which the area of a ABC having vertices
for which the area of a ABC having vertices 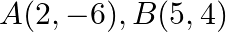 and
and 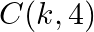 is 35 sq units.
is 35 sq units.
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the value of  for which the points
for which the points 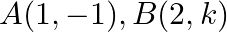 and
and 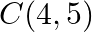 are collinear.
are collinear.
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the value of  for which the points
for which the points 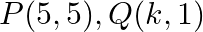 and
and 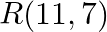 are collinear.
are collinear.
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the value of  for which the points
for which the points 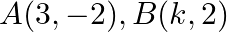 and
and 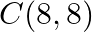 are collinear.
are collinear.
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Use determinants to show that the following points are collinear. 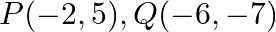 and
and 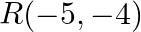
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Use determinants to show that the following points are collinear. 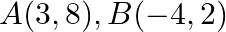 and
and 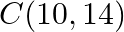
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Use determinants to show that the following points are collinear. 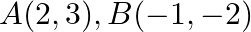 and
and 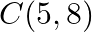
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the area of the triangle whose vertices are: 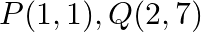 and
and 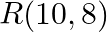
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the area of the triangle whose vertices are: 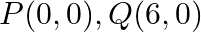 and
and 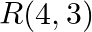
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the area of the triangle whose vertices are: 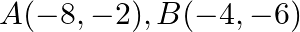 and
and 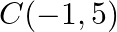
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the area of the triangle whose vertices are: 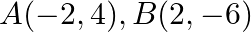 and
and 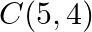
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
Find the area of the triangle whose vertices are: 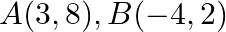 and
and 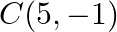
Solution: Area of a triangle $=\frac{1}{2}\left|\begin{array}{lll}\mathrm{x}_{1} & \mathrm{y}_{1} & 1 \\ \mathrm{x}_{2} & \mathrm{y}_{2} & 1 \\ \mathrm{x}_{3} & \mathrm{y}_{3}...
The general solution of the differential equation ![Rendered by QuickLaTeX.com \[{{e}^{x}}~dy\text{ }+\text{ }\left( y\text{ }{{e}^{x}}~+\text{ }2x \right)\text{ }dx\text{ }=\text{ }0\text{ }isA.\text{ }x\text{ }ey\text{ }+\text{ }{{x}^{2}}~=\text{ }C\text{ }B.\text{ }x\text{ }ey\text{ }+\text{ }{{y}^{2}}~=\text{ }C\text{ }C.\text{ }y\text{ }ex\text{ }+\text{ }{{x}^{2}}~=\text{ }C\text{ }D.\text{ }y\text{ }ey\text{ }+\text{ }{{x}^{2}}~=\text{ }C\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a5083fc3f37724ded34eb973899cb501_l3.png)
Therefore, the correct option is option(c).
The general solution of a differential equation of the type is
SOLUTION: Therefore, yje correct option is option(c).
The general solution of the differential equation is ![Rendered by QuickLaTeX.com \[\mathbf{A}.\text{ }\mathbf{xy}\text{ }=\text{ }\mathbf{C}\text{ }\mathbf{B}.\text{ }\mathbf{x}\text{ }=\text{ }\mathbf{C}{{\mathbf{y}}^{\mathbf{2}}}~\mathbf{C}.\text{ }\mathbf{y}\text{ }=\text{ }\mathbf{Cx}\text{ }\mathbf{D}.\text{ }\mathbf{y}\text{ }=\text{ }\mathbf{C}{{\mathbf{x}}^{\mathbf{2}}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1d706555279c605d673ea5651ada04da_l3.png)
Given question is Therefore, the correct option is OPTION(C)
The population of a village increases continuously at the rate proportional to the number of its inhabitants present at any time. If the population of the village was 20, 000 in 1999 and 25000 in the year 2004, what will be the population of the village in 2009?
Find a particular solution of the differential equation, given that y = 0 when x = 0.
Find a particular solution of the differential equation (x ≠ 0), given that y = 0 when x = π/2
Solve the differential equation 
Find a particular solution of the differential equation (x – y) (dx + dy) = dx – dy, given that y = –1, when x = 0. (Hint: put x – y = t)
Solve the differential equation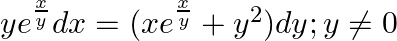
Find the particular solution of the differential equation ![Rendered by QuickLaTeX.com \[\left( \mathbf{1}\text{ }+\text{ }{{\mathbf{e}}^{\mathbf{2x}}} \right)\text{ }\mathbf{dy}\text{ }+\text{ }\left( \mathbf{1}\text{ }+\text{ }{{\mathbf{y}}^{\mathbf{2}}} \right)\text{ }{{\mathbf{e}}^{\mathbf{x}}}~\mathbf{dx}\text{ }=\text{ }\mathbf{0}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a741e3dfd2b281497b24b3de70542d10_l3.png)
, given that y = 1 when x = 0.
Find the equation of the curve passing through the point (0, π/4) whose differential equation is sin x cos y dx + cos x sin y dy = 0.
Show that the general solution of the differential equation is given by (x + y + 1) = A (1 – x – y – 2xy), where A is parameter.
Find the general solution of the differential equation 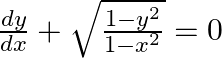
On integrating, we get, ⇒ sin-1x + sin-1y = C
Form the differential equation of the family of circles in the first quadrant which touch the coordinate axes.
(x -a)2 + (y –a)2 = a2 …………1 differentiating eq 1 with respect to x, we get, \[\begin{array}{*{35}{l}} 2\left( x-a \right)\text{ }+\text{ }2\left( y-a \right)\text{ }dy/dx~=\text{ }0 \\ \Rightarrow...
Prove that ![Rendered by QuickLaTeX.com \[{{\mathbf{x}}^{\mathbf{2}}}~-\text{ }{{\mathbf{y}}^{\mathbf{2}}}~=\text{ }\mathbf{c}\text{ }{{\left( {{\mathbf{x}}^{\mathbf{2}}}~+\text{ }{{\mathbf{y}}^{\mathbf{2}}} \right)}^{\mathbf{2}}}~\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3aba527b09857b2a939cd844ff559f93_l3.png)
is the general solution of differential equation ![Rendered by QuickLaTeX.com \[({{\mathbf{x}}^{\mathbf{3}}}-\mathbf{3x}{{\mathbf{y}}^{\mathbf{2}}})\text{ }\mathbf{dx}\text{ }=\text{ }\left( {{\mathbf{y}}^{\mathbf{3}}}-\mathbf{3}{{\mathbf{x}}^{\mathbf{2}}}\mathbf{y} \right)\text{ }\mathbf{dy},\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f17e91ba3477eee6c20ed07cc8909f13_l3.png)
where c is a parameter.
Form the differential equation representing the family of curves given by (x – a)^2 + 2y^2 = a^2, where a is an arbitrary constant.
verify that the given function (implicit or explicit) is a solution of the corresponding differential equation (iii) 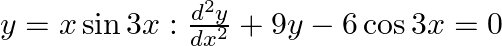 (iv)
(iv) 
verify that the given function (implicit or explicit) is a solution of the corresponding differential equation.(i)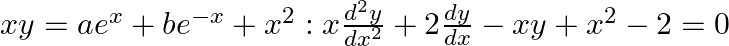 (ii)
(ii) 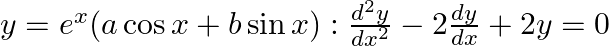
indicate its order and degree (if defined). 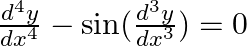
indicate its order and degree (if defined). (i) 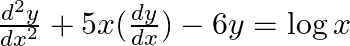 (ii)
(ii) 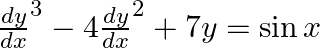
Therefore, its degree is three.
Differentiate with respect to  the functions in exercise
the functions in exercise 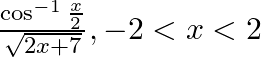
Solution: Now let's consider $y=\frac{\cos ^{-1} \frac{x}{2}}{\sqrt{2 x+7}}$ Derivating the above function: $\frac{d y}{d x}=\frac{\sqrt{2 x+7} \frac{d}{d x} \cos ^{-1} \frac{x}{2}-\cos ^{-1}...
Choose the correct answer Let A =(Fig 1) where  Then:
Then:
Fig 1= (A) Det (A) = 0 (B) Det (A) (C) Det (A) (D) Det (A) SOLUTION: Given: Matrix A = ……….(i) Since [ cannot be negative] Therefore, The correct option is option...
Choose the correct answer If x,y,z are non-zero real numbers, then the inverse of matrix A =(fig1) is
(A) (B) (C) (D) SOLUTION: Given: Matrix A = exists and unique solution is ……….(i) Now and and adj. A = = And = = = Therefore, option (A) is...
Choose the correct answer in If a,b,c are in A.P., then the determinant (fig 1) is:
fig 1: (A) 0 (B) 1 (C) (D) solution: According to question, ……….(i) Let = = [From eq. (i)] = 0 [ R2 and R3 have become identical] Therefore, option (A) is...
Solve the system of the following equations: (Using matrices):
SOLUTION: Putting and in the given equations, the matrix form of given equations is [AX= B] Here, A = X = and B = = = exists and unique solution is ……….(i) Now and and adj....
Using properties of determinants in , prove that:
=0 SOLUTION: L.H.S. = = = = = = [ C2 and C3 have become identical] = 0 = R.H.S.
Using properties of determinants in , prove that:
SOLUTION: L.H.S. = = = = = = 1 = R.H.S.
Using properties of determinants in , prove that:
SOLUTION: L.H.S. = = = = = = = = = = R.H.S.
Using properties of determinants in , prove that:
SOLUTION: L.H.S. = = = (say) ……….(i) Now = = = From eq. (i), L.H.S. = ……….(ii) Now = Expanding along third column, = = = = = From eq. (i), L.H.S. = = =...
Using properties of determinants in , prove that:
SOLUTION: L.H.S. = = = = Expanding along third column, = = = = = = = R.H.S.
Evaluate:
SOLUTION: Let = = = =
Evaluate:
SOLUTION: Let = = = = = = = = =
Let A=(fig 1), prove that (i) (adj A)^-1 = adj(A)^-1 (ii) (A^-1)^-1=A
Given: Matrix A = = Therefore, exists. and and adj. A = = B (say) = ………(i) = = Therefore, exists. and and adj. B = = = = ….(ii) Now to find (say), where C...
If A^-1 and B (in fig 1) is given , find (AB)^-1.
fig 1: , B= solution: Given: and B = Since, [Reversal law] ……….(i) Now = = Therefore, exists. and and adj. B = = From eq. (i), ...
Prove that : fig 1
fig 1: solution: L.H.S. = = = = = = = = = R.H.S. Proved.
Solve the equation: fig1
fig1: Either ……….(i) Or But this is contrary as given that . Therefore, from eq. (i), is only the solution.
If a, b and c are real numbers, and fig 1 Show that either a+b+c=0 or a=b=c
fig 1= Given: Here, Either ……….(i) Or [Expanding along first row] and and and and ……….(ii) Therefore, from eq. (i) and (ii),...
Evaluate: fig1
fig 1: Expanding along first row, = = = = = 1
Without expanding the determinant, prove that 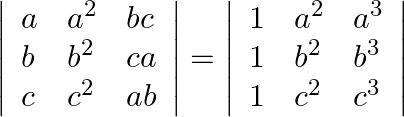
LHS: $\left|\begin{array}{lll}a & a^{2} & b c \\ b & b^{2} & c a \\ c & c^{2} & a b\end{array}\right|$ Multiplying R 1 by a $\mathrm{R} 2$ by $\mathrm{b}$ and $\mathrm{R} 3$...
Prove that the determinant 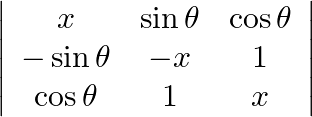 is independent of
is independent of 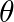 .
.
Let $\Delta=\left[\begin{array}{ccc}x & \sin \theta & \cos \theta \\ -\sin \theta & -x & 1 \\ \cos \theta & 1 & x\end{array}\right]$ $\Delta=x\left|\begin{array}{cc}-x &...
The cost of 4 kg onion, 3 kg wheat and 2 kg rice is Rs. 60. The cost of 2 kg onion, 4 kg wheat and 2 kg rice is Rs. 90. The cost of 6 kg onion, 2 k wheat and 3 kg rice is Rs. 70. Find cost of each item per kg by matrix method.
Let $x, y$ and $z$ be the per $k g$. prices of onion, wheat and rice respectively. According to given statement, we have following equations, $4 x+3 y+2 z=60$ $2 x+4 y+6 z=90$ $6 x+2 y+3 z=70$ The...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{llr}2 & -3 & 5 \\ 3 & 2 & -4 \\ 1 & 1 & -2\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-e30d4eac9a4d4350e1fb200d7e82f2e4_l3.png) find A^-1. using A^-1 solve
find A^-1. using A^-1 solve 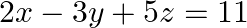
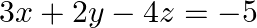
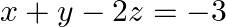
$A=\left[\begin{array}{llr}2 & -3 & 5 \\ 3 & 2 & -4 \\ 1 & 1 & -2\end{array}\right]$ $|A|=\left|\begin{array}{ccc}2 & -3 & 5 \\ 3 & 2 & -4 \\ 1 & 1 &...
Solve system of linear equations, using matrix method, in 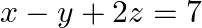
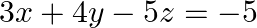
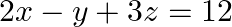
Given set of equations is : $x-y+2 z=7$ $3 x+4 y-5 z=-5$ $2 x-y+3 z=12$ This set of equation in the form of matrix is $A X=B$ $\left[\begin{array}{ccc}1 & -1 & 2 \\ 3 & 4 & -5 \\ 2...
Solve system of linear equations, using matrix method, in 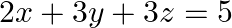
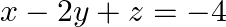
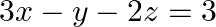
Given set of equations is : $2 x+3 y+3 z=5$ $x-2 y+z=-4$ $3 x-y-2 z=3$ This set of equation in the form of matrix is $A X=B$ $\left[\begin{array}{ccc}2 & 3 & 3 \\ 1 & -2 & 1 \\ 3...
Solve system of linear equations, using matrix method, in 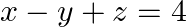 and
and 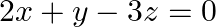 and
and 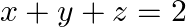
Given set of equations is $: x-y+z=4$ and $2 x+y-3 z=0$ and $x+y+z=2$ This set of equation can be written in the form of matrix as $A X=B$ $\left[\begin{array}{ccc}1 & -1 & 1 \\ 2 & 1...
Solve system of linear equations, using matrix method, in 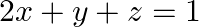 and
and 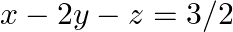 and
and 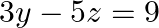
Given set of equations is $: 2 x+y+z=1$ and $x-2 y-z=3 / 2$ and $3 y-5 z=9$ This set of equation in the form of matrix is $A X=B$ $\left[\begin{array}{ccc}2 & 1 & 1 \\ 1 & -2 & -1 \\...
Solve system of linear equations, using matrix method, in 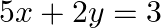 and
and 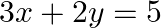
Given set of equations is : $5 x+2 y=3$ and $3 x+2 y=5$ This set of equation in the form of matrix is $A X=B$ $\left[\begin{array}{ll}5 & 2 \\ 3 & 2\end{array}\right]\left[\begin{array}{l}x...
Solve system of linear equations, using matrix method, in 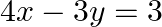 and
and 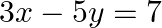
Given set of equations is : $4 x-3 y=3$ and $3 x-5 y=7$ This set of equation in the form of matrix is $A X=B$ $\left[\begin{array}{ll}4 & -3 \\ 3 &...
Solve system of linear equations, using matrix method, in 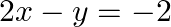 and
and 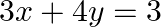
Let $A=\left[ {{a}_{ij}} \right]$ be a square matrix of order n. The adjoint of a matrix A is the transporse of the cofactor matrix of A. It is denoted by adj A. Given set of equations is : $2...
Solve system of linear equations, using matrix method, in 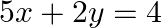 and
and 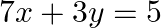
Let $A=\left[ {{a}_{ij}} \right]$ be a square matrix of order n. The adjoint of a matrix A is the transporse of the cofactor matrix of A. It is denoted by adj A. Given set of equations is : $5 x+2...
Examine the consistency of the system of equations in 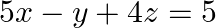 &
& 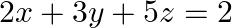 &
& 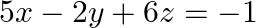
Given set of equations is: $5 x-y+4 z=5 ; 2 x+3 y+5 z=2 ; 5 x-2 y+6 z=-1$ This set of equation in the form of matrix is $A X=B$ $=140-13-76$ $=140-89$ $=51$ $\neq 0$ System of equations is...
Examine the consistency of the system of equations in 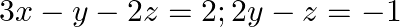 and
and 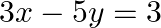
Given set of equations is : $3 x-y-2 z=2 ; 2 y-z=-1$ and $3 x-5 y=3$ This set of equation in the form of matrix is $A X=B$ $|A|=\left|\begin{array}{ccc}3 & -1 & -2 \\ 0 & 2 & -1 \\ 3...
Examine the consistency of the system of equations in 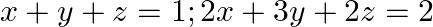 and
and 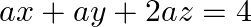
Given set of equations is $: x+y+z=1 ; 2 x+3 y+2 z=2$ and ax $+a y+2 a z=4$ This set of equationin the form of matrix is $A X=B$ $\left[\begin{array}{lll}1 & 1 & 1 \\ 2 & 3 & 2 \\ a...
Examine the consistency of the system of equations in 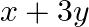 and
and 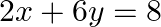
Given set of equations is : $x+3 y$ and $2 x+6 y=8$ This set of equation in the form of matrix is $A X=B$. $\left[\begin{array}{ll}1 & 3 \\ 2 & 6\end{array}\right]\left[\begin{array}{l}x \\...
Examine the consistency of the system of equations in 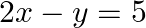 and
and 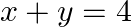
Given set of equations is $: 2 x-y=5$ and $x+y=4$ This set of equation in the form of matrix is $A X=B$, where $\mathrm{A}=\left[\begin{array}{cc}2 & -1 \\ 1 & 1\end{array}\right]$ and...
Examine the consistency of the system of equations in 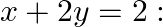 and
and 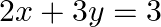
Given set of equations is : $x+2 y=2$ : and $2 x+3 y=3$ The set of equation in the form of matrix is $A X=B$, where $A=\left[\begin{array}{ll}1 & 2 \\ 2 & 3\end{array}\right]$ and...
If  is an invertible matrix of order 2 , then
is an invertible matrix of order 2 , then 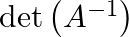 is equal to: (A) det A (B)
is equal to: (A) det A (B) 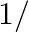 det A (C) 1 (D) 0
det A (C) 1 (D) 0
The correct answer is Option (B). Explanation: $A A^{-1}=\mid$ $\operatorname{det}\left(A A^{-1}=I\right)$ $\operatorname{det}(A) \operatorname{det}\left(A^{-1}\right)=1$...
Let  be a non-singular matrix of order
be a non-singular matrix of order  . Then |adj.
. Then |adj. 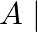 is equal to: (A)
is equal to: (A) 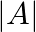 (B)
(B) 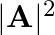 (C)
(C) 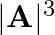 (D)
(D) 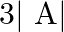
The correct answer is Option (B). Explanation: $\mid$ adj. $\left.A|=| A\right|^{n-1}=|A|^{2} \quad($ for $n=3)$
If a=(fig 1) find 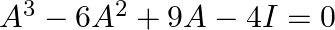 and hence find A inverse.
and hence find A inverse.
fig(1) A = = Now = = L.H.S. = = = = = = = R.H.S. Now, to find , multiplying by =
For the matrix A = (FIG 1) show that 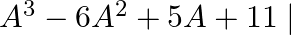 =0 Hence find A inverse.
=0 Hence find A inverse.
fig(1) A = = $A^{3}=A^{2} A=\left[\begin{array}{ccc}4 & 2 & 1 \\ -3 & 8 & -14 \\ 7 & -3 & 14\end{array}\right]\left[\begin{array}{ccc}1 & 1 & 1 \\ 1 & 2...
For the matrix ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ll}3 & 2 \\ 1 & 1\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-866d9f588aa87affb3349473fc083592_l3.png) , find the numbers
, find the numbers 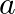 and
and 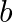 such that
such that 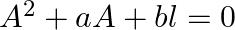 .
.
$A^{2}=A A=\left[\begin{array}{ll}3 & 2 \\ 1 & 1\end{array}\right]\left[\begin{array}{ll}3 & 2 \\ 1 & 1\end{array}\right]=\left[\begin{array}{ll}11 & 8 \\ 4 &...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{rr}3 & 1 \\ -1 & 2\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-5709cd602ca367d80c27d0813b877fa5_l3.png) , show that
, show that 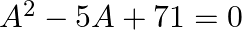 . Hence find
. Hence find 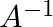 .
.
$A^{2}=A A$ $A^{2}=\left[\begin{array}{rr}3 & 1 \\ -1 & 2\end{array}\right]\left[\begin{array}{rr}3 & 1 \\ -1 & 2\end{array}\right]=\left[\begin{array}{rr}8 & 5 \\ -5 &...
Let ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ll}3 & 7 \\ 2 & 5\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1c124b99bf1a57d3fb3721bea26a7e1e_l3.png) and
and ![Rendered by QuickLaTeX.com B=\left[\begin{array}{cc}6 & 8 \\ 7 & 9\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-e3a0eb5107384b32c24edef968000318_l3.png) verify that
verify that 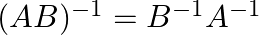
$A=\left[\begin{array}{ll}3 & 7 \\ 2 & 5\end{array}\right]$ $|\mathrm{A}|=\left|\begin{array}{ll}3 & 7 \\ 2 & 5\end{array}\right|=1 \neq 0$ $\mathrm{A}^{-1}=\frac{1}{|\mathrm{~A}|}$...
Find the inverse of each of the matrices (if it exists) given in ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc}1 & 0 & 0 \\ 0 & \cos \alpha & \sin \alpha \\ 0 & \sin \alpha & -\cos \alpha\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-04334529244081d6181667faa6b1c6cf_l3.png)
Let A = = exists. A11 = , A12 = , A13 = , A21 = , A22 = , A23 = , A31 = , A32 = , A33 = adj. A =
Find the inverse of each of the matrices (if it exists) given in ![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}1 & -1 & 2 \\ 0 & 2 & -3 \\ 3 & -2 & 4\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-e042c29b7aac5879ad60e2d53ba39a82_l3.png)
Let A = = exists. A11 = , A12 = , A13 = , A21 = , A22 = , A23 = , A31 = , A32 = , A33 = adj. A =
Find the inverse of each of the matrices (if it exists) given in ![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}2 & 1 & 3 \\ 4 & -1 & 0 \\ -7 & 2 & 1\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-ef9ad04080fa72421925cb52af2f44d9_l3.png)
Let $\mathrm{A}=\left[\begin{array}{ccc}2 & 1 & 3 \\ 4 & -1 & 0 \\ -7 & 2 & 1\end{array}\right]$ Therefore, $A^{-1}$ exists A11 = , A12 = , A13 = , A21 = , A22 = , A23 = ,...
Find the inverse of each of the matrices (if it exists) given in ![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}1 & 0 & 0 \\ 3 & 3 & 0 \\ 5 & 2 & -1\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-9a6d041e3d25f78d49c2d03a26066b9f_l3.png)
Let $A=\left[\begin{array}{lll}1 & 0 & 0 \\ 3 & 3 & 0 \\ 5 & 2 & -1\end{array}\right]$ Therefore, $A^{-1}$ exists Find adj A: 212. \text { 212. }...
Find the inverse of each of the matrices (if it exists) given in ![Rendered by QuickLaTeX.com \left[\begin{array}{lll}1 & 2 & 3 \\ 0 & 2 & 4 \\ 0 & 0 & 5\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7c2504929a778bb0735e27cd0c3c76e5_l3.png)
$\left[\begin{array}{lll}1 & 2 & 3 \\ 0 & 2 & 4 \\ 0 & 0 & 5\end{array}\right]$ Solution: Let $\mathrm{A}=\left[\begin{array}{lll}1 & 2 & 3 \\ 0 & 2 & 4 \\ 0...
Find the inverse of each of the matrices (if it exists) given in ![Rendered by QuickLaTeX.com \left[\begin{array}{ll}-1 & 5 \\ -3 & 2\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-e37f391dc108d81264eceb67aeb2556f_l3.png)
Let $A=\left[ {{a}_{ij}} \right]$ be a square matrix of order n. The adjoint of a matrix A is the transporse of the cofactor matrix of A. It is denoted by adj A. Given...
Find the inverse of each of the matrices (if it exists) given in ![Rendered by QuickLaTeX.com \left[\begin{array}{cc}2 & -2 \\ 4 & 3\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-e53bb962fa8ed0816e1952010b40c21f_l3.png)
Let $A=\left[\begin{array}{rr}2 & -2 \\ 4 & 3\end{array}\right]$ $|A|=\left[\begin{array}{cc}2 & -2 \\ 4 & 3\end{array}\right]=14 \neq 0$ Since determinant of the matrix is not zero,...
Verify 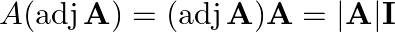 in
in ![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}1 & -1 & 2 \\ 3 & 0 & -2 \\ 1 & 0 & 3\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a1a867b9b309d524c23c55036905efd7_l3.png)
. Let A = = adj. A = A. (adj. A) = = = ……….(i) Again (adj. A). A = = = ……….(ii) And = Also = ……….(iii) From eq. (i), (ii) and (iii) A. (adj. A) = (adj. A). A...
Verify 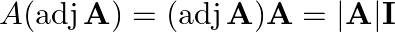 in
in ![Rendered by QuickLaTeX.com \left[\begin{array}{cc}2 & 3 \\ -4 & -6\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3d3a43d3aa5a6911398ef00d207d8087_l3.png)
Let A = adj. A = A.(adj. A) = = = …..(i) Again (adj. A). A = = = …..(ii) And = Again …..(iii) From eq. (i), (ii) and (iii) A. (adj. A) = (adj. A). A...
Find adjoint of each of the matrices in ![Rendered by QuickLaTeX.com \left[\begin{array}{ccc}1 & -1 & 2 \\ 2 & 3 & 5 \\ -2 & 0 & 1\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1c97d8dc1896c9f6190641181d8c86d5_l3.png)
Let $\mathrm{A}=\left[\begin{array}{ccc}1 & -1 & 2 \\ 2 & 3 & 5 \\ -2 & 0 & 1\end{array}\right]$ Cofactors of the above matrix are $\mathrm{A}_{11}=+\left|\begin{array}{ll}3...
Find adjoint of each of the matrices in ![Rendered by QuickLaTeX.com \left[\begin{array}{ll}1 & 2 \\ 3 & 4\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d3ff67a5276113f580775455111647e6_l3.png)
Let $A=$ $\left[\begin{array}{ll}1 & 2 \\ 3 & 4\end{array}\right]$ Cofactors of the above matrix are 11 $A_{11}=4$ $A_{12}=-3$ $\mathrm{A}_{21}=-2$ $A_{22}=1$ adj....
Using Cofactors of elements of third column, evaluate  .
. 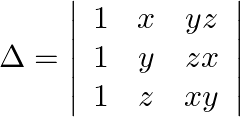
Elements of third column of are A13 = Cofactor of = A23 = Cofactor of = A33 = Cofactor of = = = = = = = = = =
Using Cofactors of elements of second row, evaluate 
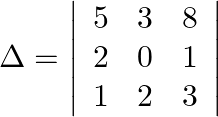
Find Cofactors of elements of second row: $A_{21}=$ Cofactor of element $a_{21}=(-1)^{2+1}\left|\begin{array}{cc}3 & 8 \\ 2 & 3\end{array}\right|-(-1)^{3}(9-16)=7$ $A_{22}=C$ ofactor of...
Write Minors and Cofactors of the elements of following determinants: (i) (ii)
(ii) 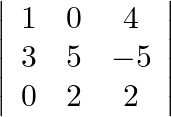
(i) $\left|\begin{array}{lll}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right|$ Find Minors and cofactors of elements: Say, $M_{i j}$ is minor of element $a_{i j}$ and...
Write Minors and Cofactors of the elements of following determinants: (i) 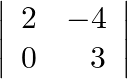 (ii)
(ii) 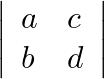
Find Minors of elements: Say, $M_{i j}$ is minor of element $a_{i i}$ $\mathrm{M}_{11}=$ Minor of element $\mathrm{a}_{11}=3$ $\mathrm{M}_{12}=$ Minor of element $\mathrm{a}_{12}=0$...
If area of triangle is 35 sq units with vertices 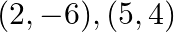 and
and 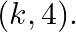 Then
Then  is (A) 12 (B)
is (A) 12 (B) 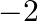 (C)
(C) 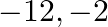 (D)
(D) 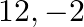
The correct option is OPTION(D) Given: Area of triangle = Modulus of = 35 Modulus of = 35 Taking positive sign, Taking negative sign,
(i) Find equation of line joining 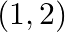 and
and 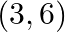 using determinants. (ii) Find equation of line joining
using determinants. (ii) Find equation of line joining 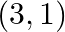 and
and 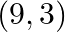 using determinants.
using determinants.
Let $A(x, y)$ be any vertex of a triangle. All points are on one line if area of triangle is zero. $\frac{1}{2}[x(2-6)-y(1-3)+1(6-6)]=0$ $-4 x+2 y=0$ $y=2 x$ Which is equation of line. (ii) Let...
Find values of  if area of triangle is 4 sq. units and vertices are (i)
if area of triangle is 4 sq. units and vertices are (i) 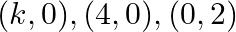 (ii)
(ii) 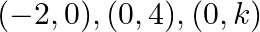
(i) $\frac{1}{2}[k(0-2)-0+1(8-0)]=4$ $1 / 2(-2 k+4)=4$ $-k+4=4$ Now: $-k+4=\pm 4$ $-k+4=4$ and $-k+4=-4$ $\mathrm{k}=0$ and $\mathrm{k}=8$ $\frac{1}{2}\left|\begin{array}{lll}x_{1} & y_{1} &...
Show that points: 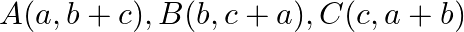 are collinear.
are collinear.
Points are collinear if area of triangle is equal to zero. i.e. Area of triangle $=0$ Area of Triangle $=\frac{1}{2}\left|\begin{array}{ccc}a & b+c & 1 \\ b & c+a & 1 \\ c & a+b...
Find area of the triangle with vertices at the point given in each of the following:(iii) 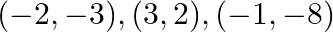
Area $=\frac{1}{2}\left|\begin{array}{ccc}-2 & -3 & 1 \\ 3 & 2 & 1 \\ -1 & -8 & 1\end{array}\right|$ $=\frac{1}{2}[-2(10)+3(4)-22]$ $=15$ sq. Units
Find area of the triangle with vertices at the point given in each of the following: (i) 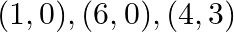 (ii)
(ii) 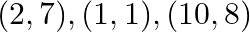
Formula for Area of triangle: $\frac{1}{2}\left|\begin{array}{lll}x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1 \\ x_{3} & y_{3} & 1\end{array}\right|$ (i)...
Choose the corrrect answer Which of the following is correct (A) Determinant is a square matrix. (B) Determinant is a number associated to a matrix. (C) Determinant is a number associated to a square matrix. (D) None of these
The correct option is Option (C) Since, Determinant is a number associated to a square matrix.
Choose the corrrect answer Let  be a square matrix of order
be a square matrix of order  , then
, then 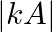 is equal to (A)
is equal to (A) 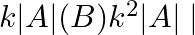 (C)
(C) 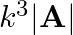 (D)
(D) 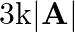
The correct option is Option (C). Let A = be a square matrix of order 3 x 3. ……….(i) = [From eq. (i)]
By using properties of determinants, show that: 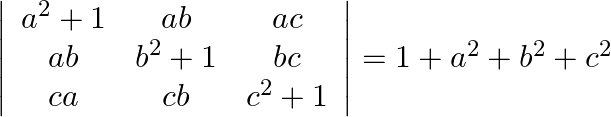
LHS $\left|\begin{array}{ccc}a^{2}+1 & a b & a c \\ a b & b^{2}+1 & b c \\ c a & c b & c^{2}+1\end{array}\right|$ Multiplying by respectively and then dividing the...
By using properties of determinants, show that: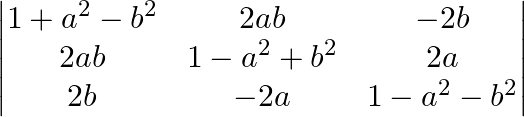
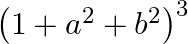
LHS $\mathrm{C}_{1} \rightarrow \mathrm{C}_{1}-b \mathrm{C}_{3}$ and $\mathrm{C}_{2} \rightarrow \mathrm{C}_{2}+a \mathrm{C}_{3}$ $=\left|\begin{array}{ccc}1+a^{2}+b^{2} & 0 & -2 b \\ 0...
By using properties of determinants, show that: ![Rendered by QuickLaTeX.com \[\left|\begin{array}{ccc} 1 & x & x^{2} \\ x^{2} & 1 & x \\ x & x^{2} & 1 \end{array}\right|=\left(1-x^{3}\right)^{2}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-31bd0220c4c348d80de219a56446e48b_l3.png)
![Rendered by QuickLaTeX.com \[\left|\begin{array}{ccc} 1 & x & x^{2} \\ x^{2} & 1 & x \\ x & x^{2} & 1 \end{array}\right|=\left(1-x^{3}\right)^{2}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-31bd0220c4c348d80de219a56446e48b_l3.png)
L.H.S. = = = = = = = = = = = = = R.H.S. Proved.
By using properties of determinants, show that: (i) 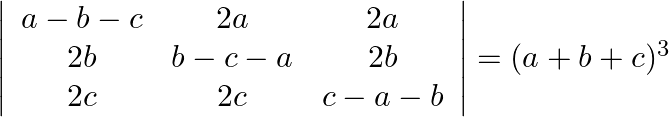 (ii)
(ii) 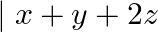
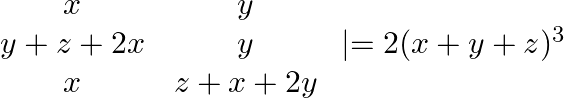
LHS $\left|\begin{array}{ccc}a-b-c & 2 a & 2 a \\ 2 b & b-c-a & 2 b \\ 2 c & 2 c & c-a-b\end{array}\right|$ $\mathrm{R}_{1} \rightarrow...
By using properties of determinants, show that: ![Rendered by QuickLaTeX.com \[\text { (i) }\left|\begin{array}{ccc} x+4 & 2 x & 2 x \\ 2 x & x+4 & 2 x \\ 2 x & 2 x & x+4 \end{array}\right|=(5 x+4)(4-x)^{2}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-761ecebc01ac7ac73d668008d102850f_l3.png)
![Rendered by QuickLaTeX.com \[\text { (ii) }\left|\begin{array}{ccc} y+k & y & y \\ y & y+k & y \\ y & y & y+k \end{array}\right|=k^{2}(3 y+k)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-96eaf73e0a5c4da52bd9f5777af34135_l3.png)
![Rendered by QuickLaTeX.com \[\text { (i) }\left|\begin{array}{ccc} x+4 & 2 x & 2 x \\ 2 x & x+4 & 2 x \\ 2 x & 2 x & x+4 \end{array}\right|=(5 x+4)(4-x)^{2}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-761ecebc01ac7ac73d668008d102850f_l3.png)
![Rendered by QuickLaTeX.com \[\text { (ii) }\left|\begin{array}{ccc} y+k & y & y \\ y & y+k & y \\ y & y & y+k \end{array}\right|=k^{2}(3 y+k)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-96eaf73e0a5c4da52bd9f5777af34135_l3.png)
(i) LHS = [operating and ] = = = R.H.S. (ii) L.H.S. = = = = [operating and ] = = = = R.H.S. Proved.
By using properties of determinants, show that: 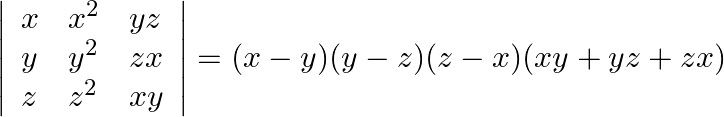
LHS= $\left|\begin{array}{lll}x & x^{2} & y z \\ y & y^{2} & z x \\ z & z^{2} & x y\end{array}\right|$ Mulitiplying $R_{1}, R_{2}, R_{3}$ by $x, y, z$ respectively...
By using properties of determinants, show that:(i) 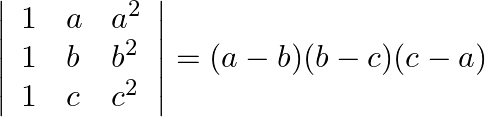 (ii)
(ii) 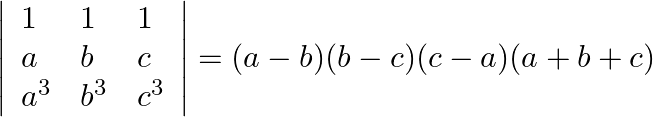
(i) LHS: $\left|\begin{array}{lll}1 & a & a^{2} \\ 1 & b & b^{2} \\ 1 & c & c^{2}\end{array}\right|$ $\mathrm{R}_{2} \rightarrow \mathrm{R}_{2}-\mathrm{R}_{1}$ and...
Using the properties of determinants and without expanding, prove that 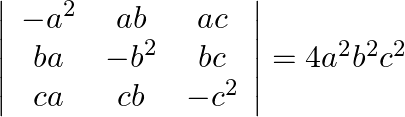
Solving L.H.S $\left| \begin{matrix} -{{a}^{2}} & ab & ac \\ ba & -{{b}^{2}} & bc \\ ca & cb & -{{c}^{2}} \\ \end{matrix} \right|$ Taking a common from${{R}_{1}}$,b common...
Using the properties of determinants and without expanding, prove that 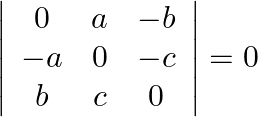
Let $\Delta=\left|\begin{array}{ccc}0 & a & -b \\ -a & 0 & -c \\ b & c & 0\end{array}\right|$ Taking (-1) common from all the 3 rows. Again, interchanging rows and columns,...
Using the properties of determinants and without expanding, prove that 
LHS: Applying: $R_{1} \rightarrow R_{1}+R_{2}+R_{3}$ $\left|\begin{array}{ccc}b+c+c+a+a+b & q+r+r+p+p+q & y+z+z+x+x+y \\ c+a & r+p & z+x \\ a+b & p+q & x+y\end{array}\right|$...
Using the properties of determinants and without expanding, prove that: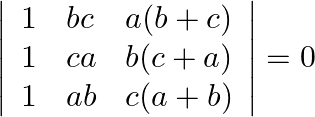
$\left|\begin{array}{ccc}1 & b c & a(b+c) \\ 1 & c a & b(c+a) \\ 1 & a b & c(a+b)\end{array}\right|$ Applying: $\mathrm{C}_{3}->\mathrm{C}_{3}+\mathrm{C}_{2}$...
Using the properties of determinants and without expanding, prove that: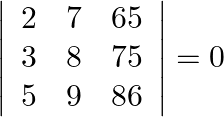
$\left|\begin{array}{lll}2 & 7 & 65 \\ 3 & 8 & 75 \\ 5 & 9 & 86\end{array}\right|$ Applying: $\mathrm{C}_{3}->\mathrm{C}_{3}-\mathrm{C}_{1}$ $\left|\begin{array}{lll}2...
Using the properties of determinants and without expanding, prove that: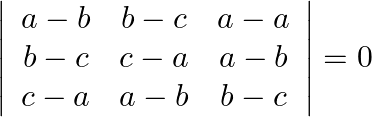
$\left|\begin{array}{ccc}a-b & b-c & a-a \\ b-c & c-a & a-b \\ c-a & a-b & b-c\end{array}\right|$ Applying: $\mathrm{C}_{1} \rightarrow...
Using the properties of determinants and without expanding, prove that: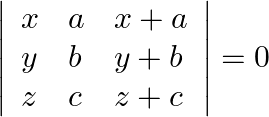
$\left|\begin{array}{lll}x & a & x+a \\ y & b & y+b \\ z & c & z+c\end{array}\right|=0$ L.H.S. $\left|\begin{array}{lll}x & a & x+a \\ y & b & y+b \\ z &...
If 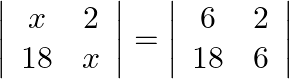 then
then  is equal to (A) 6 (B)
is equal to (A) 6 (B)  (C)
(C) 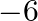 (D) 0
(D) 0
The correct option is Option (B). Reason : $x^2{\prime} =36$ $x=\pm 6$
Find values of  , if (i)
, if (i) 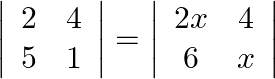 (ii)
(ii) 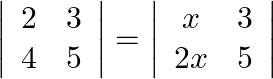
(i) $\left|\begin{array}{ll}2 & 4 \\ 5 & 1\end{array}\right|=\left|\begin{array}{cc}2 x & 4 \\ 6 & x\end{array}\right|$ $2-20=2 \times^{-2}-24$ $2 \times^{\prime} 2=6$ $x^{-2}=3$ or...
If A = 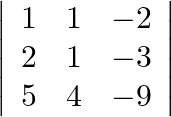 find |A|
find |A|
$A=\left|\begin{array}{ccc}1 & 1 & -2 \\ 2 & 1 & -3 \\ 5 & 4 & -9\end{array}\right|$ $|A|=\left|\begin{array}{ccc}1 & 1 & -2 \\ 2 & 1 & -3 \\ 5 & 4 &...
Evaluate the determinants(iii) 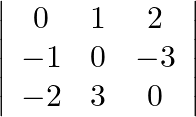 (iv)
(iv) 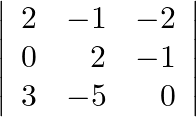
(iii) = 0 + 6 – 6 = 0 (iv) =5
Evaluate the determinants (i) 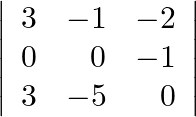 (ii)
(ii) 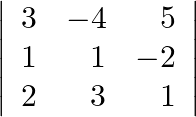
(i) $\left|\begin{array}{rrr}3 & -1 & -2 \\ 0 & 0 & -1 \\ 3 & -5 & 0\end{array}\right|=3\left|\begin{array}{rr}0 & -1 \\ -5 &...
If A =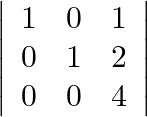 then show that | 3 A | = 27 | A |
then show that | 3 A | = 27 | A |
$3 A=\left[\begin{array}{ccc}3 & 0 & 3 \\ 0 & 3 & 6 \\ 0 & 0 & 12\end{array}\right]$ LHS: $|3 A|=\left|\begin{array}{lll}3 & 0 & 3 \\ 0 & 3 & 6 \\ 0 & 0...
If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ll}1 & 2 \\ 4 & 2\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-9e263b57f5b17d5ce7c731eb0cc6b8e0_l3.png) then show that
then show that 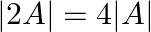 .
.
$A=\left[\begin{array}{ll}1 & 2 \\ 4 & 2\end{array}\right]$ $2 \mathrm{~A}=\left[\begin{array}{ll}2 & 4 \\ 8 & 4\end{array}\right]$ L.H.S. $=|2 A|=\left|\begin{array}{ll}2 & 4 \\...
Evaluate the following determinants 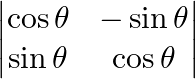 &
& 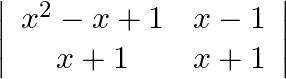
(i) $\left| \begin{matrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \\ \end{matrix} \right|$ = $\cos \theta X\cos \theta -(-\sin \theta )Xsin\theta =1$ (ii) $\left|...
Evaluate the following determinants 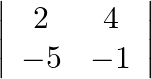
$\left|\begin{array}{cc}2 & 4 \\ -5 & -1\end{array}\right|=2(-1)-4(-5)=18$
