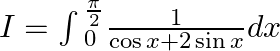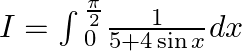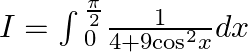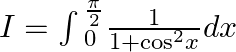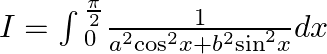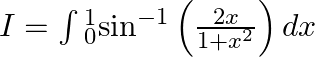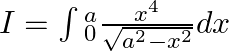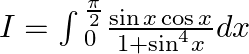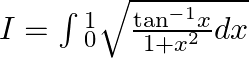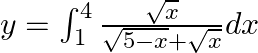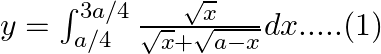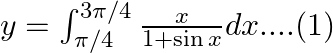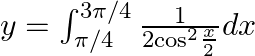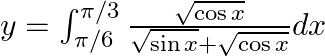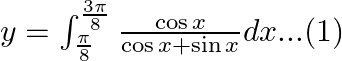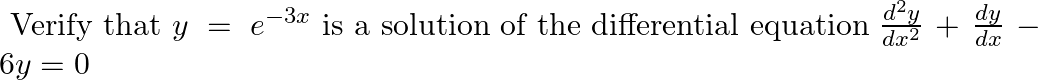Compute the shortest distance between the lines
Find the shortest distance between the given lines.
Find the shortest distance between the given lines.
Find the shortest distance between the given lines.
Find the shortest distance between the given lines.
Find the shortest distance between the given lines.
Find the shortest distance between the given lines.
Find the shortest distance between the given lines.
Find the shortest distance between the given lines. ![Rendered by QuickLaTeX.com \[\begin{array}{l} \square \vec{r}=(\hat{i}+\hat{j})+\lambda(2 \hat{i}-\hat{j}+\hat{k}) \\ \vec{r}=(2 \hat{i}+\hat{j}-\hat{k})+\mu(3 \hat{i}-5 \hat{j}+2 \hat{k}) \end{array}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2f8ab5b81e582387cb9ae472791476e4_l3.png)
![Rendered by QuickLaTeX.com \[\begin{array}{l} \square \vec{r}=(\hat{i}+\hat{j})+\lambda(2 \hat{i}-\hat{j}+\hat{k}) \\ \vec{r}=(2 \hat{i}+\hat{j}-\hat{k})+\mu(3 \hat{i}-5 \hat{j}+2 \hat{k}) \end{array}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2f8ab5b81e582387cb9ae472791476e4_l3.png)
Answer Given equations: r¯=(ı^+ȷ^)+λ(2ı^-ȷ^+k^) \overline{\mathrm{r}}=(\hat{\imath}+\hat{\jmath})+\lambda(2 \hat{\imath}-\hat{\jmath}+\hat{\mathrm{k}})...
Find the shortest distance between the given lines. ![Rendered by QuickLaTeX.com \[\begin{array}{l} \square \vec{r}=(\hat{i}+\hat{j})+\lambda(2 \hat{i}-\hat{j}+\hat{k}) \\ \vec{r}=(2 \hat{i}+\hat{j}-\hat{k})+\mu(3 \hat{i}-5 \hat{j}+2 \hat{k}) \end{array}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2f8ab5b81e582387cb9ae472791476e4_l3.png)
![Rendered by QuickLaTeX.com \[\begin{array}{l} \square \vec{r}=(\hat{i}+\hat{j})+\lambda(2 \hat{i}-\hat{j}+\hat{k}) \\ \vec{r}=(2 \hat{i}+\hat{j}-\hat{k})+\mu(3 \hat{i}-5 \hat{j}+2 \hat{k}) \end{array}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2f8ab5b81e582387cb9ae472791476e4_l3.png)
Answer Given equations: r¯=(ı^+ȷ^)+λ(2ı^-ȷ^+k^) \overline{\mathrm{r}}=(\hat{\imath}+\hat{\jmath})+\lambda(2 \hat{\imath}-\hat{\jmath}+\hat{\mathrm{k}})...
If A(1, 2, 3), B(4, 5, 7), C(-4, 3, -6) and D(2, 9, 2) are four given points then find the angle between the lines AB and CD.
Answer Given - A = (1,2,3) B = (4,5,7) C = (-4,3,-6) D = (2,9,2) Formula to be used – If P = (a,b,c) and Q = (a’,b’,c’),then the direction ratios of the line PQ is given by ((a’-a),(b’-b),(c’-c))...
Show that the lines x = – y = 2z and x + 2 = 2y – 1 = – z + 1 are perpendicular to each other.
To prove – The lines are perpendicular to each other Direction ratios of L1 = (2,-2,1) Direction ratios of L2 = (2,1,-2) Tip – If (a,b,c) be the direction ratios of the first line and (a’,b’,c’) be...
prove that
To find – The value of λ Direction ratios of L1 = (-3,2λ,2) Direction ratios of L2 = (3λ,1,-5) Tip – If (a,b,c) be the direction ratios of the first line and (a’,b’,c’) be that of the second, then...
To prove – The lines are perpendicular to each other Direction ratios of L1 = (2,-3,4) Direction ratios of L2 = (2,4,2) Tip – If (a,b,c) be the direction ratios of the first line and (a’,b’,c’) be...
Find the angle between each of the following pairs of lines:
To find – Angle between the two pair of lines Direction ratios of L1 = (-3,-2,0) Direction ratios of L2 = (1,-3,2) Tip – If (a,b,c) be the direction ratios of the first line and (a’,b’,c’) be that...
Find the angle between each of the following pairs of lines:
To find – Angle between the two pair of lines Direction ratios of L1 = (1,0,-1) Direction ratios of L2 = (3,4,5) Tip – If (a,b,c) be the direction ratios of the first line and (a’,b’,c’) be that of...
Find the angle between each of the following pairs of lines:
To find – Angle between the two pair of lines Direction ratios of L1 = (2,1,-3) Direction ratios of L2 = (3,2,-1) Tip – If (a,b,c) be the direction ratios of the first line and (a’,b’,c’) be that of...
Find the angle between each of the following pairs of lines:
To find – Angle between the two pair of lines Direction ratios of L1 = (4,3,5) Direction ratios of L2 = (1,-1,1) Tip – If (a,b,c) be the direction ratios of the first line and (a’,b’,c’) be that of...
Find the angle between each of the following pairs of lines
To find – Angle between the two pair of lines Direction ratios of L1 = (1,1,2) Direction ratios of L2 = (3,5,4) Tip – If (a,b,c) be the direction ratios of the first line and (a’,b’,c’) be that of...
Find the angle between each of the following pairs of lines:
To find – Angle between the two pair of lines Direction ratios of L1 = (2,-2,1) Direction ratios of L2 = (1,2,-2) Tip – If (a,b,c) be the direction ratios of the first line and (a’,b’,c’) be that of...
Find the angle between each of the following pairs of lines
Tip – If (a,b,c) be the direction ratios of the first line and (a’,b’,c’) be that of the second, then the angle between these pair of lines is given by
The position vectors of three points A, B and C are
It can thus be written as: A = (-4,2,-3) B = (1,3,-2) C = (-9,1,-4) To prove – A, B and C are collinear Formula to be used – If P = (a,b,c) and Q = (a’,b’,c’),then the direction ratios of the line...
Find the values of λ and μ so that the points A(-1, 4, -2), B(λ, μ 1) and C(0, 2, -1) are collinear.
Answer Given - A = (-1,4,-2) B = (λ,μ,1) C = (0,2,-1) To find – The value of λ and μ so that A, B and C are collinear Formula to be used – If P = (a,b,c) and Q = (a’,b’,c’),then the direction ratios...
Find the values of λ and μ so that the points A(3, 2, -4), B(9, 8, -10) and C(λ, μ -6) are collinear.
Answer Given - A = (3,2,-4) B = (9,8,-10) C = (λ,μ,-6) To find – The value of λ and μ so that A, B and C are collinear Formula to be used – If P = (a,b,c) and Q = (a’,b’,c’),then the direction...
Find the value of λ for which the points A(2, 5, 1), B(1, 2, -1) and C(3, λ, 3) are collinear.
Answer Given - A = (2,5,1) B = (1,2,-1) C = (3,λ,3) To find – The value of λ so that A, B and C are collinear Formula to be used – If P = (a,b,c) and Q = (a’,b’,c’),then the direction ratios of the...
Show that the points A(2, 3, -4), B(1, -2, 3) and C(3, 8, -11) are collinear.
Answer Given - A = (2,3,-4) B = (1,-2,3) C = (3,8,-11) To prove – A, B and C are collinear Formula to be used – If P = (a,b,c) and Q = (a’,b’,c’),then the direction ratios of the line PQ is given by...
Show that the points A(2, 1, 3), B(5, 0, 5) and C(-4, 3, -1) are collinear.
Answer Given - A = (2,1,3) B = (5,0,5) C = (-4,3,-1) To prove – A, B and C are collinear Formula to be used – If P = (a,b,c) and Q = (a’,b’,c’),then the direction ratios of the line PQ is given by...
Find the image of the point (2, -1, 5) in the line
Find the image of the point $(2,-1,5)$ in the line r→=(11i^-2j^-8k^)+λ(10i^-4j^-11k^) \overrightarrow{\mathrm{r}}=(11 \hat{i}-2 \hat{j}-8 \hat{\mathrm{k}})+\lambda(10 \hat{i}-4...
Find the image of the point (5, 9, 3) in the line
Find the image of the point $(5,9,3)$ in the line $\frac{\mathrm{x}-1}{2}=\frac{\mathrm{y}=2}{3}=\frac{\mathrm{z}-3}{4}$. Answer Given: Equation of line is...
Find the image of the point (0, 2, 3) in the line
Find the image of the point $(0,2,3)$ in the line $\frac{\mathrm{x}+3}{5}=\frac{\mathrm{y}-1}{2}=\frac{\mathrm{z}+4}{3}$. Answer Given: Equation of line is...
Find the coordinates of the foot of the perpendicular drawn from the point A(1, 8, 4) to the line joining the points B(0, -1, 3) and C(2, -3, -1).
Find the coordinates of the foot of the perpendicular drawn from the point $A(1,8,4)$ to the line joining the points $B(0,-1,3)$ and $C(2,-3,-1)$ Answer Given: perpendicular drawn from point...
Find the coordinates of the foot of the perpendicular drawn from the point A(1, 2, 1) to the line joining the points B(1, 4, 6) and C(5, 4, 4).
Find the coordinates of the foot of the perpendicular drawn from the point $A(1,2,1)$ to the line joining the points $B(1,4,6)$ and $C(5,4,4)$. Answer Given: perpendicular drawn from point...
Find the vector equation of a line passing through the point having the position vector
Find the vector equation of a line passing through the point having the position vector $(\hat{i}+2 \hat{j}-3 \hat{k})$ and parallel to the line joining the points with position vectors...
Find the vector equation of a line passing through the point A(3, -2, 1) and parallel to the line joining the points B(-2, 4, 2) and C(2, 3, 3). Also, find the Cartesian equations of the line.
Find the vector equation of a line passing through the point $A(3,-2,1)$ and parallel to the line joining the points $\mathrm{B}(-2,4,2)$ and $\mathrm{C}(2,3,3) .$ Also, find the Cartesian equations...
Find the vector and Cartesian equations of the line joining the points whose position vectors are
Find the vector and Cartesian equations of the line joining the points whose position vectors are $(\hat{i}-2 \hat{j}+\hat{k})$ and $(\hat{i}+3 \hat{j}-2 \hat{k})$ Answer Given: line passes through...
Find the vector and Cartesian equations of the line passing through the points A(2, -3, 0) and B(-2, 4, 3).
Find the vector and Cartesian equations of the line passing through the points $A(2,-3,0)$ and $B(-2,4,$, 3). Answer Given: line passes through the points $(2,-3,0)$ and $(-2,4,3)$ To find: equation...
Find the vector and Cartesian equations of the line passing through the points A(3, 4, -6) and B(5, -2, 7).
Find the equations of the line passing through the point $(1,-2,3)$ and parallel to the line $\frac{\mathrm{x}-6}{3}=\frac{\mathrm{y}-2}{-4}=\frac{\mathrm{Z}+7}{5}$. Also find the vector form of...
Find the coordinates of the foot of the perpendicular drawn from the point (1, 2, 3) to the line
Find the coordinates of the foot of the perpendicular drawn from the point $(1,2,3)$ to the line $\frac{\mathrm{x}-6}{3}=\frac{\mathrm{y}-7}{2}=\frac{\mathrm{z}-7}{-2}$. Also, find the length of the...
Show that the lines and do not intersect each other.
Show that the lines $\frac{\mathrm{x}-1}{2}=\frac{\mathrm{y}+1}{3}=z$ and $\frac{\mathrm{x}+1}{5}=\frac{\mathrm{y}-2}{1}, Z=2$ do not intersect each other. Answer Given: The equations of the two...
Show that the lines and intersect each other. Also, find the point of their intersection.
Show that the lines $\frac{\mathrm{x}-1}{2}=\frac{\mathrm{y}-2}{3}=\frac{\mathrm{Z}-3}{4}$ and $\frac{\mathrm{x}-4}{5}=\frac{\mathrm{y}-1}{2}=\mathrm{Z}$ intersect each other. Also, find the point...
Prove that the lines
Prove that the lines $\frac{\mathrm{x}-4}{1}=\frac{\mathrm{y}+3}{4}=\frac{\mathrm{z}+1}{7}$ and $\frac{\mathrm{x}-1}{2}=\frac{\mathrm{y}+1}{-3}=\frac{\mathrm{z}+10}{8}$ intersect each other and find...
Find the Cartesian and vector equations of the line passing through the point (1, 2, -4) and
Find the Cartesian and vector equations of the line passing through the point $(1,2,-4)$ and perpendicular to each of the lines...
Find the equations of the line passing through the point (-1, 3, -2) and perpendicular to each of the lines and
Find the equations of the line passing through the point $(-1,3,-2)$ and perpendicular to each of the lines $\frac{\mathrm{X}}{1}=\frac{\mathrm{y}}{2}=\frac{\mathrm{Z}}{3}$ and...
Find the Cartesian and vector equations of a line which passes through the point (1, 2, 3) and is parallel to the line
Find the Cartesian and vector equations of a line which passes through the point $(1,2,3)$ and is parallel to the line $\frac{-\mathrm{X}-2}{1}=\frac{\mathrm{y}+3}{7}=\frac{2 Z-6}{3}$ Answer Given:...
Find the equations of the line passing through the point (1, -2, 3) and parallel to the line Also find the vector form of this equation so obtained.
Find the equations of the line passing through the point $(1,-2,3)$ and parallel to the line $\frac{\mathrm{x}-6}{3}=\frac{\mathrm{y}-2}{-4}=\frac{\mathrm{Z}+7}{5}$. Also find the vector form of...
Find the Cartesian equations of the line which passes through the point (1, 3, -2) and is parallel to the line Also, find the vector form of the equations so obtained.
Find the Cartesian equations of the line which passes through the point $(1,3,-2)$ and is parallel to the line given by $\frac{\mathrm{x}+1}{3}=\frac{\mathrm{y}-4}{5}=\frac{\mathrm{z}+3}{-6}$. Also,...
The Cartesian equations of a line are 3x + 1 = 6y – 2 = 1 – z. Find the fixed point through which it passes, its direction ratios and also its vector equation.
The Cartesian equations of a line are $3 x+1=6 y-2=1-z$. Find the fixed point through which it passes, its direction ratios and also its vector equation. Answer Given: Cartesian equation of line are...
The Cartesian equations of a line Find the vector equation of the line.
The Cartesian equations of a line are $\frac{\mathrm{x}-3}{2}=\frac{\mathrm{y}+2}{-5}=\frac{\mathrm{Z}-6}{4}$. Find the vector equation of the line. Answer Given: Cartesian equation of line...
A line is drawn in the direction and it passes through a point with position vector Find the equations of the line in the vector as well as Cartesian forms.
A line is drawn in the direction of $(\hat{\mathrm{i}}+\hat{\mathrm{j}}-2 \hat{\mathrm{k}})$ and it passes through a point with position vector $(2 \hat{i}-\hat{j}-4 \hat{k}) .$ Find the equations...
Find the vector equation of the line passing through the point with position vector and parallel to the vector Deduce the Cartesian equations of the line.
Find the vector equation of the line passing through the point with position vector $(2 \hat{\mathrm{i}}+\hat{\mathrm{j}}-5 \hat{\mathrm{k}})$ and parallel to the vector $(\hat{i}+3...
A line passes through the point (2, 1, -3) and is parallel to the vector Find the equations of the line in vector and Cartesian forms.
A line passes through the point $(2,1,-3)$ and is parallel to the vector $(\hat{\mathrm{i}}-2 \hat{\mathrm{j}}+3 \hat{\mathrm{k}})$. Find the equations of the line in vector and Cartesian forms....
A line passes through the point (3, 4, 5) and is parallel to the vector Find the equations of the line in the vector as well as Cartesian forms.
Answer Given: line passes through point $(3,4,5)$ and is parallel to $2 \hat{\imath}+2 \hat{\jmath}-3 \hat{k}$ To find: equation of line in vector and Cartesian forms Formula Used: Equation of a...
For the binary operation ×10 set S = {1, 3, 7, 9}, find the inverse of 3.
Answer: 1 ×10 1 = remainder obtained by dividing 1 × 1 by 10 = 1 3 ×10 7 = remainder obtained by dividing 3 × 7 by 10 = 1 7 ×10 9 = remainder obtained by dividing 7 × 9 by 10 = 3 Composition table:...
Construct the composition table for ×5 on set Z5 = {0, 1, 2, 3, 4}
Answer: 1 ×5 1 = remainder obtained by dividing 1 × 1 by 5 = 1 3 ×5 4 = remainder obtained by dividing 3 × 4 by 5 = 2 4 ×5 4 = remainder obtained by dividing 4 × 4 by 5 = 1 Composition table: ×5 0 1...
Construct the composition table for ×6 on set S = {0, 1, 2, 3, 4, 5}.
Answer: 1 ×6 1 = remainder obtained by dividing 1 × 1 by 6 = 1 3 ×6 4 = remainder obtained by dividing 3 × 4 by 6 = 0 4 ×6 5 = remainder obtained by dividing 4 × 5 by 6 = 2 Composition table: ×6 0 1...
Construct the composition table for +5 on set S = {0, 1, 2, 3, 4}
Answer: 1 +5 1 = remainder obtained by dividing 1 + 1 by 5 = 2 3 +5 1 = remainder obtained by dividing 3 + 1 by 5 = 2 4 +5 1 = remainder obtained by dividing 4 + 1 by 5 = 3 Composition Table: +5 0 1...
Construct the composition table for ×4 on set S = {0, 1, 2, 3}.
Answer: Given, ×4 on set S = {0, 1, 2, 3} 1 ×4 1 = remainder obtained by dividing 1 × 1 by 4 = 1 0 ×4 1 = remainder obtained by dividing 0 × 1 by 4 = 0 2 ×4 3 = remainder obtained by dividing 2 × 3...
Let * be a binary operation on Z defined by a * b = a + b – 4 for all a, b ∈ Z. (i) Show that * is both commutative and associative. (ii) Find the identity element in Z
Answers: (i) Consider, a, b ∈ Z a * b = a + b – 4 = b + a – 4 = b * a a * b = b * a, ∀ a, b ∈ Z Then, * is commutative on Z. a * (b * c) = a * (b + c – 4) = a + b + c -4 – 4 = a + b + c – 8 (a * b)...
Let * be a binary operation on Q0 (set of non-zero rational numbers) defined by a * b = (3ab/5) for all a, b ∈ Q0. Show that * is commutative as well as associative. Also, find its identity element, if it exists.
Answer: Consider, a, b ∈ Q0 a * b = (3ab/5) = (3ba/5) = b * a a * b = b * a, for all a, b ∈ Q0 a * (b * c) = a * (3bc/5) = [a (3 bc/5)] /5 = 3 abc/25 (a * b) * c = (3 ab/5) * c = [(3 ab/5)...
Let * be a binary operation on Q – {-1} defined by a * b = a + b + ab for all a, b ∈ Q – {-1}. Then, (i) Show that * is both commutative and associative on Q – {-1} (ii) Find the identity element in Q – {-1}
Answers: (i) Consider, a, b ∈ Q – {-1} a * b = a + b + ab = b + a + ba = b * a a * b = b * a, ∀ a, b ∈ Q – {-1} a * (b * c) = a * (b + c + b c) = a + (b + c + b c) + a (b + c + b c) = a + b +...
Let * be a binary operation on Q – {-1} defined by a * b = a + b + ab for all a, b ∈ Q – {-1}. Then, Show that every element of Q – {-1} is invertible. Also, find inverse of an arbitrary element.
Answer: Consider, a ∈ Q – {-1} and b ∈ Q – {-1} be the inverse of a. a * b = e = b * a a * b = e and b * a = e a + b + ab = 0 and b + a + ba = 0 b (1 + a) = – a Q – {-1} b = -a/1 + a Q – {-1}...
Let A = R0 × R, where R0 denote the set of all non-zero real numbers. A binary operation ‘O’ is defined on A as follows: (a, b) O (c, d) = (ac, bc + d) for all (a, b), (c, d) ∈ R0 × R. (i) Show that ‘O’ is commutative and associative on A (ii) Find the identity element in A
Answers: (i) Consider, X = (a, b) Y = (c, d) ∈ A, ∀ a, c ∈ R0 b, d ∈ R X O Y = (ac, bc + d) Y O X = (ca, da + b) X O Y = Y O X, ∀ X, Y ∈ A O is not commutative on A. X = (a, b) Y = (c, d) a Z = (e,...
Let A = R0 × R, where R0 denote the set of all non-zero real numbers. A binary operation ‘O’ is defined on A as follows: (a, b) O (c, d) = (ac, bc + d) for all (a, b), (c, d) ∈ R0 × R. Find the invertible element in A.
Answer: Consider, F = (m, n) be the inverse in A ∀ m ∈ R0 and n ∈ R X O F = E F O X = E (am, bm + n) = (1, 0) and (ma, na + b) = (1, 0) Considering (am, bm + n) = (1, 0) am = 1 m = 1/a And bm + n =...
Let * be a binary operation on Z defined by a * b = a + b – 4 for all a, b ∈ Z. Find the invertible element in Z.
Answer: Consider, a ∈ Z and b ∈ Z be the inverse of a. a * b = e = b * a a * b = e and b * a = e a + b – 4 = 4 and b + a – 4 = 4 b = 8 – a ∈ Z Hence, 8 – a is the inverse of a ∈...
Find the identity element in the set of all rational numbers except – 1 with respect to * defined by a * b = a + b + ab
Answer: Consider, e be the identity element in I+ with respect to * such that a * e = a = e * a, ∀ a ∈ Q – {-1} a * e = a and e * a = a, ∀ a ∈ Q – {-1} a + e + ae = a and e + a + ea = a, ∀ a ∈ Q –...
Find the identity element in the set I+ of all positive integers defined by a * b = a + b for all a, b ∈ I+.
Answer: Consider, e be the identity element in I+ with respect to * a * e = a = e * a, ∀ a ∈ I+ a * e = a and e * a = a, ∀ a ∈ I+ a + e = a and e + a = a, ∀ a ∈ I+ e = 0, ∀ a ∈ I+ Hence, 0 is the...
Let $I=\int _{\pi /6}^{\pi /2}\frac{\cos ecx\cot x}{1+\cos e{{c}^{2}}x}dx=\int _{\pi /6}^{\pi /2}\frac{\cos x}{1+{{\sin }^{2}}x}dx$ Let $\sin x=t$ $\Rightarrow \cos xdx=dt$ Also, when...
Let $I=\int _{1}^{2}\frac{1}{x{{(1+{{\log }_{e}}x)}^{2}}}dx$ Let $1+{{\log }_{e}}x=t$ $\Rightarrow \frac{1}{x}dx=dt$ Also, when $x=1,t=1$and when $x=2$ $t=1+{{\log }_{e}}2$ Hence, $I=\int...
Let $I=\int _{0}^{{{\left( \frac{\pi }{2} \right)}^{\frac{1}{3}}}}{{x}^{2}}\sin \left( {{x}^{3}} \right)dx$ Let ${{x}^{3}}=t$ $\Rightarrow 3{{x}^{2}}=dt$ Also, when $x=0,t=0$and when $t=\frac{\pi...
Let $I=\int _{\pi /4}^{\pi /2}\frac{\cos x}{{{\left( \cos \left( \frac{x}{2} \right)+\sin \left( \frac{x}{2} \right) \right)}^{3}}}dx$ $\cos x={{\cos }^{2}}\left( \frac{x}{2} \right)-{{\sin...
Let $I=\int _{2}^{3}\frac{2-x}{\sqrt{5x-6-{{x}^{2}}}}dx$ Let $2-x=\frac{ad}{dx}\left( 5x-6-{{x}^{2}} \right)+b$ $=-2ax+5a+b$ Hence $-2a=-1$and $5a+b=2$ Solving these equations, We get and...
Let $I=\int _{0}^{\pi /2}\left( \sqrt{\tan x}+\sqrt{\cos tx} \right)dx=\int _{0}^{\pi /2}\frac{\sin x+\cos x}{\sqrt{\sin x\cos x}}dx$ Let $\sin x-\cos x=t$ $\Rightarrow \left( \cos x+\sin x...
Let $I=\int _{0}^{1}\frac{1-{{x}^{2}}}{{{(1+{{x}^{2}})}^{2}}}dx$ Let $x=\tan t$ $\Rightarrow dx={{\sec }^{2}}tdt$ Also, when $x=0,t=0$and when $x=1,t=\frac{\pi }{4}$ Hence, $I'=\int _{0}^{\pi...
Let $I=\int _{0}^{1}{{x}^{3}}\sqrt{1+3{{x}^{4}}}dx$ Let $1+3{{x}^{4}}=t$ $\Rightarrow 12{{x}^{3}}dx=dt$ Also, when $x=0,t=1$and when $x=1,t=4$ $I=\frac{1}{12}\int _{1}^{4}\sqrt{t}dt$...
Let $I=\int _{0}^{9}\frac{1}{1+\sqrt{x}}$ Let $\sqrt{x}=u$ $\Rightarrow \frac{1}{2\sqrt{x}}=dx=du$ Or $dx=2udu$ $=\frac{1}{2u}dx$ Also, when $x=0,u=0$and $x=9,u=3$ Hence, $I=\int...
Let $I=\int _{0}^{a}{{\sin }^{-1}}\sqrt{\frac{x}{a+x}}dx$ Let $x=a{{\tan }^{2}}y$ $\Rightarrow dx=2a\tan y{{\sec }^{2}}ydy$ Also, when $x=0,y=0$ And when $x=a$ $y=\frac{\pi }{4}$ Hence, $I=\int...
Let $I=\int _{0}^{1}{{\sin }^{-1}}\sqrt{x}dx$ Let $\sqrt{x}=1$ $\Rightarrow \frac{1}{2\sqrt{x}}=dx=dt$ Or $dx=2tdt$ When $x=0,t=0$ And when $x=1,t=1$ Hence, $I=2\int _{0}^{1}t{{\sin }^{-1}}tdt$...
Let $I=\int _{0}^{1}x{{(a{{\tan }^{-1}}x)}^{2}}dx$ Using integration by parts, we get $I=\frac{{{\left( {{\tan }^{-1}}x \right)}^{2}}{{x}^{2}}}{2}|_{0}^{1}-\int _{0}^{1}\frac{2{{\tan...
Let $I=\int _{0}^{1}{{\left( {{\cos }^{-1}}x \right)}^{2}}dx$ Let $x=\cos t\Rightarrow dx=-\sin tdt$ Also, when $x=0,t=\frac{\pi }{2}$ And when $x=1,t=0$ Hence, $I=-\int _{\pi /2}^{0}{{t}^{2}}\sin...
Let \[I=\int _{\pi /3}^{\pi /2}\frac{\sqrt{1+\cos x}}{(1-\cos x)\frac{5}{2}}dx\] Using $1+\cos x=2\cos {{x}^{2}}\left( \frac{x}{2} \right)$ $1-\cos x=2{{\sin }^{2}}\left( \frac{x}{2} \right)$ we get...
Let $I=\int _{0}^{\pi /2}\frac{\sin 2x}{{{\sin }^{4}}x+{{\cos }^{4}}x}dx$ Using $\sin 2x=2\sin x\cos x$, we get $=2\int _{0}^{\pi /2}\frac{\tan x{{\sec }^{2}}x}{({{\tan }^{4}}x+1)}dx$ $I=\int...
Let $I=\int _{0}^{\pi /2}\frac{\sin x\cos x}{{{\cos }^{2}}x+3\cos x+2}dx$ Let $\cos x=t$ $\Rightarrow -\sin xdx=dt$ Also, when $x=0,t=1$ And when $t=0$ $x=\frac{\pi }{2}$ Hence, $I=-\int...
Let $I=\int _{0}^{\pi /4}\frac{{{\tan }^{3}}x}{1+\cos 2x}dx$ Using $1+\cos 2x=2{{\cos }^{2}}x$, we get $I=\frac{1}{2}\int _{0}^{\pi /4}{{\tan }^{3}}x{{\sec }^{2}}xdx$ Let $\tan x=t$ $\Rightarrow...
Let $I=\int _{0}^{\pi }\frac{1}{3+\cos x+2\sin x}dx$ Using $\sin x=\frac{2\tan \left( \frac{x}{2} \right)}{1+{{\tan }^{2}}\left( \frac{x}{2} \right)}$ $\cos x=\frac{1-{{\tan }^{2}}\left( \frac{x}{2}...
$f(x)$is continuous in $\left[ a,b \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=(b-a)/n$ Here $h=\left( b-a \right)/n$ $\int...
$f\left( x \right)$is continuous in $\left[ 1,3 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=(b-a)/n$ Here $h=2/n$ $\int _{1}^{3}\left(...
$f\left( x \right)$is continuous in $\left[ 0,2 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=(b-a)/n$ Here $h=2/n$ $\int _{0}^{2}\left(...
Since it is modulus function so we need to break the function and then solve it $f\left( x \right)=\int _{0}^{1/3}\left( 1-3x \right)dx+\int _{1/3}^{1}(3x-1)dx$it is continuous in $\left[ 0,1...
$f\left( x \right)$is continuous in $\left[ 0,3 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=(b-a)/n$ Here $h=3/n$ $\int _{0}^{3}\left(...
$f\left( x \right)$is continuous in $\left[ 0,2 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=(b-a)/n$ Here $h=2/n$ $\int _{0}^{2}\left(...
$f(x)$is continuous in $\left[ 2,4 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=(b-a)/n$ Here $h=3/n$ \[\int...
Let $I=\int{_{0}^{\frac{\pi }{2}}}\frac{1}{\cos x+2\sin x}dx$ Using $\sin x=\frac{2\tan \left( \frac{x}{2} \right)}{1+{{\tan }^{2}}\left( \frac{x}{2} \right)}$ And $\cos x=\frac{1-{{\tan...
Let $I=\int{_{0}^{\frac{\pi }{2}}}\frac{1}{\cos x+2\sin x}dx$ Using $\sin x=\frac{2\tan \left( \frac{x}{2} \right)}{1+{{\tan }^{2}}\left( \frac{x}{2} \right)}$ And $\cos x=\frac{1-{{\tan...
Let $I=\int{_{0}^{\pi }}\frac{1}{5+4\cos x}dx$ Using, we get $\cos x=\frac{1-{{\tan }^{2}}\left( \frac{x}{2} \right)}{1+{{\tan }^{2}}\left( \frac{x}{2} \right)}$ $I=\int{_{0}^{\pi...
$I=\int{_{0}^{\pi }}\frac{1}{6-\cos x}dx$ Using, we get $\cos x=\frac{1-{{\tan }^{2}}\left( \frac{x}{2} \right)}{1+{{\tan }^{2}}\left( \frac{x}{2} \right)}$ $I=\int{_{0}^{\pi }}\frac{1-{{\tan...
Let $I=\int{_{0}^{\frac{\pi }{2}}}\frac{1}{5+4\sin x}dx$ $$$\sin x=\frac{2\tan \left( \frac{x}{2} \right)}{1+{{\tan }^{2}}\left( \frac{x}{2} \right)}$...
Let $I=\int{_{0}^{\frac{\pi }{2}}}\frac{1}{4+9{{\cos }^{2}}x}dx$ Dividing by ${{\cos }^{2}}x$ in numerator and denominator, we get $$$I=\int{_{0}^{\frac{\pi }{2}}}\frac{{{\sec }^{2}}x}{2{{\sec...
Let $I=\int{_{0}^{\frac{\pi }{2}}}\frac{1}{1+{{\cos }^{2}}x}dx$ Dividing by ${{\cos }^{2}}x$in numerator and denominator, we get $I=\int{_{0}^{\frac{\pi }{2}}}\frac{{{\sec...
Let $I=\int{_{0}^{\frac{\pi }{2}}\frac{1}{{{a}^{2}}{{\cos }^{2}}x+{{b}^{2}}{{\sin }^{2}}x}dx}$ Dividing by ${{\cos }^{2}}x$in numerator and denominator, we get $I=\int{_{0}^{\frac{\pi...
Let $I=\int{_{0}^{\frac{\pi }{2}}}\sqrt{1+\sin x}dx$ Using and ${{\sin }^{2}}\frac{x}{2}+\cos \frac{x}{2}=1$ $\sin x=2\sin \frac{x}{2}\cos \frac{x}{2}$ $I=\int{_{0}^{\frac{\pi }{2}}}\sqrt{{{\left(...
Let $I=\int{_{0}^{\frac{\pi }{2}}}\sqrt{1+\cos x}dx$ Using, we get $1+\cos x=2{{\cos }^{2}}\frac{x}{2}$ $I=\sqrt{2\sin }\left( \frac{x}{2} \right)\left| _{0}^{\frac{\pi }{2}} \right.=2$
Let $I=\int{_{0}^{1}}{{\sin }^{-1}}\left( \frac{2x}{1+{{x}^{2}}} \right)dx$ Let $\int{\left( x \right)}={{\sin }^{-1}}\left( \frac{2x}{1+{{x}^{2}}} \right)$ Let $x=\tan \theta $ $\Rightarrow \theta...
Let $I=\int{_{0}^{2}x\sqrt{2-xdx}}$ Using the property that, we get $\int{_{a}^{b}f(x)dx=\int{_{a}^{b}f(a+b-x)dx}}$ $I=\int{_{0}^{2}(2-x)\sqrt{xdx}}$...
Let $I=\int{_{0}^{1}\frac{x}{\sqrt{{{a}^{2}}+{{x}^{2}}}}dx}$ Let ${{a}^{2}}+{{x}^{2}}={{t}^{2}}$ $\Rightarrow xdx=tdt.$ Also when $x=0,t=a$ And when x=a, $t=\sqrt{2a}$ Hence ,...
Let $I=\int{_{0}^{a}\frac{{{x}^{4}}}{\sqrt{{{a}^{2}}-{{x}^{2}}}}dx}$ Let x=a sin t a cos t dt=dx also, when $x=0,t=0$ and when x=a , $t=\frac{\pi }{2}$ Hence, $I=\int{_{0}^{\frac{\pi...
Let $I=\int{_{0}^{\sqrt{2}}\sqrt{2-{{x}^{2}}}dx}$ Consider, $I=\int{_{0}^{\sqrt{2}}\sqrt{2-{{x}^{2}}}dx}$ Let x=a sin t $\Rightarrow a\cos ttdt=dx$ Also, when $x=0,t=0$ and when x=a, $t=\frac{\pi...
Let $I=\int{_{0}^{a}\sqrt{{{a}^{2}}-{{x}^{2}}}dx}$ Let x=a sin t $\Rightarrow a\cos tdt=dx$ Also, $x=0,t=0$ And When $x=a,t=\frac{\pi }{2}$ Hence, $I=\int{_{0}^{\frac{\pi...
$I=\int{_{0}^{\frac{\pi }{2}}\frac{\sin x\cos x}{1+{{\sin }^{4}}x}dx}$ Let ${{\sin }^{2}}x=t$ $\Rightarrow 2\sin x\cos x=dt.$ Also, When $x=0,t=0$ And When $x=\frac{\pi }{2},t=1.$ Hence,...
Let $I=\int{_{0}^{\frac{\pi }{2}}\sqrt{\sin x{{\cos }^{5}}xdx}}$ Let $\sin x=t$ $\Rightarrow \cos xdx=dt.$ Also, When $x=0,t=0$ And When $x=\frac{\pi }{2},t=1.$ Consider ${{\cos }^{5}}x={{\cos...
Let $I=\int{_{0}^{\frac{\pi }{2}}\frac{\sin x}{\sqrt{1+\cos x}}dx}$ Let $1+cosx=t$ $\Rightarrow -\sin xdx=dt.$ Also, when $x=0,t=2$ And When $x=\frac{\pi }{2},t=1$ Hence,...
Let $I=\int{_{0}^{1}}\sqrt{\frac{{{\tan }^{-1}}x}{1+{{x}^{2}}}dx}$ Let ${{\tan }^{-1}}x=t$ $\Rightarrow \frac{1}{1+{{x}^{2}}}dx=dt$ When $x=1$, $t=\frac{\pi }{4}$ Hence, $I=\int{_{0}^{\frac{\pi...
$f\left( x \right)$is continuous in $\left[ 0,2 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=(b-a)/n$ Here $h=2/n$ $\int _{0}^{2}\left(...
$f\left( x \right)$is continuous in $\left[ 1,3 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=(b-a)/n$ $\int _{1}^{3}\left(...
$f\left( x \right)$is continuous in $\left[ 1,3 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=(b-a)/n$ Here $h=3/n$ \[\int...
$f\left( x \right)$is continuous in $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=(b-a)/n$ Here $h=3/n$ \[\int...
$f\left( x \right)$is continuous in $\left[ 2,5 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=\left( b-a \right)/n$ Here $h=3/n$ $\int...
$f(x)$is continuous in $\left[ 2,5 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+r-h)$, where $h=(b-a)/n$ Here $h=3/n$ $\int...
$f(x)$is continuous in $\left[ 0,3 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=b-a/n$ Here $h=3/n$ \[\int...
$f\left( x \right)$is continuous in $\left[ 1,3 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=\left( b-a \right)/n$ Here $h=2/n$ $\int...
$f(x)$is continuous in $\left[ 1,2 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=(b-a)/n$ Here $h=1/n$ $\int...
$f(x)$is continuous in $\left[ 0,2 \right]$ $\int _{a}^{b}f(x)dx=\underset{n\to \infty }{\mathop{\lim }}\,h\sum _{r=0}^{n-1}f(a+rh)$, where $h=(b-a)/n$ Here $h=2n$ $\int _{0}^{2}\left( x+4...
$y=\int _{0}^{4}\left| x \right|+\left| x-2 \right|+\left| x-4 \right|dx$ $y=\int _{0}^{2}\left| x \right|+\left| x-2 \right|+\left| x-4 \right|dx+\int _{2}^{4}\left| x \right|+\left| x-2...
$y=\int _{0}^{4}f(x)dx$ $y=\int _{0}^{2}f(x)dx+\int _{2}^{4}f(x)dx$ $y=\int _{0}^{2}3{{x}^{2}}+4dx+\int _{2}^{4}9x-2dx$ $y=\left( {{x}^{3}}+4x \right)_{0}^{2}+\left( \frac{9{{x}^{2}}}{2}-2x...
$y=\int _{1}^{3}f(x)dx$ $y=\int _{1}^{2}f(x)dx+\int _{2}^{3}f(x)dx$ $y=\int _{1}^{2}2x+1dx+\int _{2}^{3}{{x}^{2}}+1dx$ $y=\left( {{x}^{2}}+x \right)_{1}^{2}+\left( \frac{{{x}^{3}}}{3}+x...
We know that $\left| \sin x \right|=-\sin x$in $\left[ -\pi /4,0 \right)$ $\left| \sin x \right|=\sin x$in $\left[ 0,\pi /4 \right]$ $y=\int _{-\pi /4}^{0}\left| \sin x \right|dx+\int _{0}^{\pi...
We know that $\left| \cos x \right|=\cos x$in $\left[ 0,\pi /2 \right)$ $\left| \cos x \right|=-\cos x$in $\left[ \pi /2,3\pi /2 \right)$ $\left| \cos x \right|=\cos x$in $\left[ 3\pi /2,2\pi ...
We know that $\left| x-5 \right|=-(x-5)$in $\left[ 0,5 \right)$ $\left| x-5 \right|=(x-5)$in $\left[ 5,8 \right]$ $y=\int _{0}^{5}\left| x-5 \right|dx+\int _{5}^{8}\left| x-5 \right|dx$ $y=\int...
From the differential equation of the family of circles having centers on y-axis and radius  units.
units.
Equation of the family of circles having centers on $y$-axis and radius $2$ units can be represented by $(x)^{2}+(y-a)^{2}=4$, where $a$ is an arbitrary constant. $(y-a)^{2}+x^{2}=4(1)$...
We know that $\left| x+1 \right|=-(x+1)$in $\left[ -2,-1 \right)$ $\left| x+1 \right|=(x+1)$in $\left[ -1,2 \right]$ $y=\int _{-2}^{-1}\left| x+1 \right|dx+\int _{-1}^{2}\left| x+1 \right|dx$...
We know that $\left| x \right|=-x$in $\left[ -1,0 \right)$ $\left| x \right|=x$in $\left[ 0,1 \right]$ $y=\int _{-1}^{0}{{e}^{\left| x \right|}}dx+\int _{0}^{1}{{e}^{\left| x \right|}}dx$ $y=\int...
$y=\int _{-\pi }^{\pi }{{x}^{12}}{{\sin }^{9}}xdx......(1)$ Use king theorem of definite integral $\int _{a}^{b}f(t)dt=\int _{a}^{b}f(a+b-t)dt$ $y=\int _{-\pi }^{\pi }{{\left( \pi -\pi -x...
$y=\int _{-\pi }^{\pi }{{\sin }^{75}}x+{{x}^{125}}dx.....(1)$ Use king theorem of definite integral $\int _{a}^{b}f(t)dt=\int _{a}^{b}f(a+b-t)dt$ $y=\int _{-\pi }^{\pi }{{\sin }^{75}}\left( \pi -\pi...
$y=\int _{-a}^{a}{{x}^{3}}\sqrt{{{a}^{2}}-{{x}^{2}}dx}.....(1)$ Use king theorem of definite integral $\int _{a}^{b}f(t)dt=\int _{a}^{b}f(a+b-t)dt$ $y=\int...
Form the differential equation of the family of all circles touching the 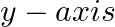 at the origin.
at the origin.
Equation of the family of all circles touching the $y$-axis at the origin can be represented by $(x-a)^{2}+y^{2}=a^{2}$, where $a$ is an arbitrary constants. $(x-a)^{2}+y^{2}=a^{2}(1)$...
Form the differential equation of the family of hyperbolas having foci on the 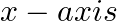 and centers at the origin.
and centers at the origin.
Equation of the family of an ellipse having foci on the $y$-axis and centers at the origin can be represented by $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ $......(1)$ Differentiating the above...
Let $x=\tan t$ $\Rightarrow dx={{\sec }^{2}}tdt$ At $x=0,t=0$ At $x=1,t=\pi /4$ \[y=\int _{0}^{\pi /4}\frac{\log \left( 1+\tan t \right)}{1+{{\tan }^{2}}t}{{\sec }^{2}}tdt\] \[y=\int _{0}^{\pi...
Use integration by parts $\int I\times IIdt=I\int IIdt-\int \frac{d}{dt}I\left( \int IIdt \right)dt$ $y=\log x\int \frac{\sqrt{1}}{\sqrt{1-{{x}^{2}}}}dx-\int \frac{d}{dx}\log x\left( \int...
Form the differential equation of the family of curves given by 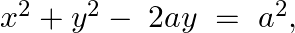 where a is an arbitrary constant.
where a is an arbitrary constant.
Equation of the family of curves, $x^{2}+y^{2}-2 a y=a^{2}$, where $a$ is an arbitrary constant. $\begin{array}{l} x^{2}-2 a x+a^{2}+2 y^{2}=a^{2} \\ x^{2}-2 a x+2 y^{2}=0 \end{array}$...
Let, $x=\sin t$ $\Rightarrow dx=\cos tdt$ At $x=0,t=0$ At $x=1,t=\pi /2$ $y=\int _{0}^{\pi /2}\frac{{{\sin }^{-1}}\sin t}{\sin t}\cos tdt$ $y=\int _{0}^{\pi /2}\frac{t\cos t}{\sin t}dt$ $y=\int...
Form the differential equation of the family of an ellipse having foci on the 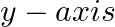 and centers at the origin.
and centers at the origin.
Equation of the family of an ellipse having foci on the $y$-axis and centers at the origin can be represented by...
Use integration by parts $\int I\times IIdx=I\int IIdx-\int \frac{d}{dx}I\left( \int IIdx \right)dx$ $y=x\int \cot xdx-\int \frac{d}{dx}x\left( \int \cot xdx \right)dx$ $y=\left( x\log \sin x...
Use king theorem of definite integral $\int _{a}^{b}f(x)=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{1}^{4}\frac{\sqrt{4+1-x}}{\sqrt{4+1-x}+\sqrt{x}}dx$ $y=\int...
Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{a/4}^{3a/4}\frac{\sqrt{\frac{3a}{4}+\frac{a}{4}-x}}{\sqrt{\frac{3a}{4}+\frac{a}{4}-x}+\sqrt{x}}dx$...
Form the differential equation of the family of curves given by 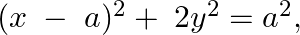 where
where 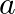 is an arbitrary constant.
is an arbitrary constant.
Equation of the family of curves, $(x-a)^{2}+2 y^{2}=a^{2}$, where $a$ is an arbitrary constant. $\begin{array}{l} x^{2}-2 a x+a^{2}+2 y^{2}=a^{2} \\ x^{2}-2 a x+2 y^{2}=0 \end{array}$...
Form the differential equation of the family of parabolas having a vertex at the origin and axis along positive 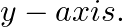
Equation of the family of parabolas having a vertex at the origin and axis along positive $y$-axis can be represented by $(x)^{2}=4 a y$, where $a$ is an arbitrary constants. $x^{2}=4 a y(1)$...
Mark the tick against the correct answer in the following: If the points 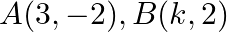 and
and 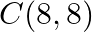 are collinear then the value of
are collinear then the value of  is
is
A. 2
B. 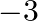
C. 5
D. 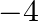
Solution: Option(C) To find: Area of $A B C$ Given: $A(3,-2), B(k, 2)$ and $C(8,8)$ The formula used: $\Delta=\frac{1}{2}\left|\begin{array}{lll}x_{1} & y_{1} & 1 \\ x_{2} & y_{2} &...
Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{\pi /4}^{3\pi /4}\frac{\left( \frac{3\pi }{4}+\frac{\pi }{4}-x \right)}{1+\sin \left( \frac{3\pi...
Mark the tick against the correct answer in the following: The vertices of a a  are
are 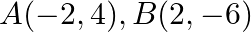 and
and 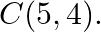 The area of a
The area of a  is
is
A. 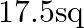 units
units
B. 35 sq units
C. 32 sq units
D. 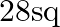 units
units
Solution: Option(B) To find: Area of $A B C$ Given: $A(-2,4), B(2,-6)$ and $C(5,4)$ Formula used: $\Delta=\frac{1}{2}\left|\begin{array}{lll}x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1 \\...
$y=\frac{1}{2}\int _{\pi /4}^{3\pi /4}{{\sec }^{2}}\frac{x}{2}dx$ $y=\frac{1}{2}\left( \frac{\frac{\tan x}{2}}{\frac{1}{2}} \right)_{\pi /4}^{3\pi /4}$ $y=\tan \frac{3\pi }{8}-\tan \frac{\pi }{8}$...
Mark the tick against the correct answer in the following: The solution set of the equation 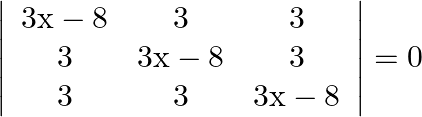 is
is
A. 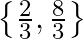
B. 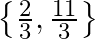
C. 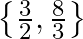
D. None of these
Solution: Option(B) To find: Value of $x$ We have, $\left|\begin{array}{ccc}3 x-8 & 3 & 3 \\ 3 & 3 x-8 & 3 \\ 3 & 3 & 3 x-8\end{array}\right|=0$ Applying $\mathrm{R}_{1}...
Mark the tick against the correct answer in the following: The solution set of the equation 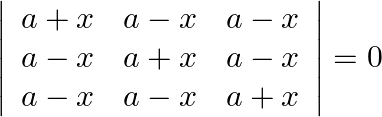 is
is
A. 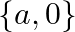
B. 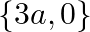
C. 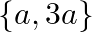
D. None of these
Solution: Option(B) To find: Value of $x$ We have, $\left|\begin{array}{ccc}a+x & a-x & a-x \\ a-x & a+x & a-x \\ a-x & a-x & a+x\end{array}\right|=0$ Applying...
Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{\pi /6}^{\pi /3}\frac{\sqrt{\cos \left( \frac{\pi }{3}+\frac{\pi }{6}-x \right)}}{\left( \sqrt{\sin...
Form the differential equation of the family of circles passing through the fixed point 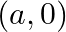 and
and 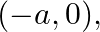 where
where 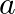 is the parameter.
is the parameter.
Now, it is not necessary that the centre of the circle will lie on origin in this case. Hence let us assume the coordinates of the centre of the circle be $(0, \mathrm{~h})$. Here, $\mathrm{h}$ is...
Mark the tick against the correct answer in the following: The solution set of the equation 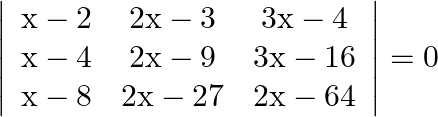 is
is
A. 
B. 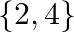
C. 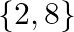
D. 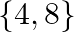
Solution: Option(A) To find: Value of $x$ We have, $\left|\begin{array}{ccc}x-2 & 2 x-3 & 3 x-4 \\ x-4 & 2 x-9 & 3 x-16 \\ x-8 & 2 x-27 & 3 x-64\end{array}\right|=0$ Applying...
Form the differential equation of the family of curves 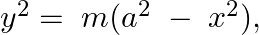 where
where 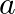 and
and 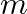 are parameters.
are parameters.
Equation of the family of curves, $y^{2}=m\left(a^{2}-x^{2}\right)$, where $a$ and $m$ are parameters. Differentiating the above equation with respect to $x$ on both sides, we have,...
Mark the tick against the correct answer in the following: The solution set of the equation 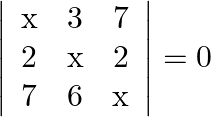 is
is
A. 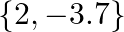
B. 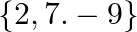
C. 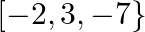
D. none of these
Solution: Option(C) To find: Value of $x$ We have, $\left|\begin{array}{lll}\mathrm{x} & 3 & 7 \\ 2 & \mathrm{X} & 2 \\ 7 & 6 & \mathrm{x}\end{array}\right|=0$ Applying...
Use king theorem of definite integral $\int _{a}^{b}f(x)dx=\int _{a}^{b}f(a+b-x)dx$ $y=\int _{\pi /8}^{3\pi /8}\frac{\cos \left( \frac{3\pi }{8}+\frac{\pi }{8}-x \right)}{\sin \left( \frac{3\pi...
Mark the tick against the correct answer in the following: If 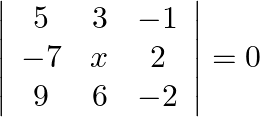 then
then 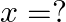
A. 0
B. 6
C. 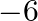
D. 9
Solution: Option(C) To find: Value of $\mathrm{x}$ We have, $\left|\begin{array}{ccc}5 & 3 & -1 \\ -7 & x & 2 \\ 9 & 6 & -2\end{array}\right|=0$ Applying $R_{1} \rightarrow 2...
Form the differential equation of the family of circles having centers on the 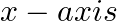 and radius unity.
and radius unity.
Equation of the family of circles having centers on the $x$-axis and radius unity can be represented by $(x-a)^{2}+(y)^{2}=1$, where $a$ is an arbitrary constants. $(x-a)^{2}+y^{2}=1(1)$...
Mark the tick against the correct answer in the following: 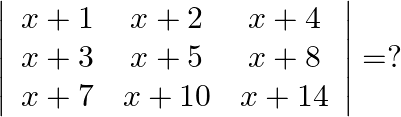
A. 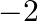
B. 2
C. 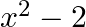
D. 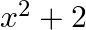
Solution: Option(A) To find: Value of $\left|\begin{array}{ccc}\mathrm{x}+1 & \mathrm{x}+2 & \mathrm{x}+4 \\ \mathrm{x}+3 & \mathrm{x}+5 & \mathrm{x}+8 \\ \mathrm{x}+7 &...
Form the differential equation of the family of curves 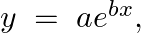 where
where 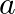 and
and 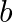 are arbitrary constants.
are arbitrary constants.
Equation of the family of curves, $y=a e^{b x}$, where $a$ and $b$ are arbitrary constants. Differentiating the above equation with respect to $x$ on both sides, we have, $\begin{array}{l} y=a e^{b...
![Rendered by QuickLaTeX.com \[y=\int _{0}^{\pi /2}\log \left( \frac{\sin x}{\cos x}+\frac{\cos x}{\sin x} \right)dx\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-a679411f8191078aadb81574c6f2b9f5_l3.png)
\[y=\int _{0}^{\pi /2}\log \frac{1}{\sin x\cos x}dx\] \[y=-\left( \int _{0}^{\pi /2}\log \sin xdx+\int _{0}^{\pi /2}\log \cos xdx \right)\] Let, $I=\int _{0}^{\pi /2}\log \sin xdx......(1)$ Use king...
Mark the tick against the correct answer in the following: 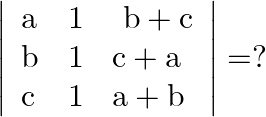
A. 
B. 
C. 
D. 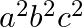
Solution: Option(C) To find: Value of $\left|\begin{array}{lll}a & 1 & b+c \\ b & 1 & c+a \\ c & 1 & a+b\end{array}\right|$ We have, $\left|\begin{array}{lll}a & 1 &...
Mark the tick against the correct answer in the following: 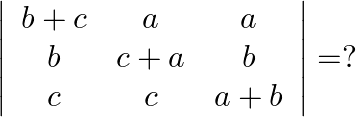
A. 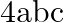
B. 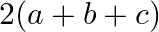
C. 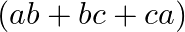
D. none of these
Solution: Option(A) To find: Value of $\left|\begin{array}{ccc}b+c & a & a \\ b & c+a & b \\ c & c & a+b\end{array}\right|$ We have, $\left|\begin{array}{ccc}b+c & a...
Mark the tick against the correct answer in the following: 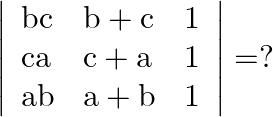
A. 
B. 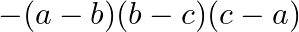
C. 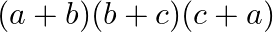
D. None of these
Solution: Option(A) To find: Value of $\left|\begin{array}{lll}\mathrm{bc} & \mathrm{b}+\mathrm{c} & 1 \\ \mathrm{ca} & \mathrm{a}+\mathrm{c} & 1 \\ \mathrm{ab} &...
Mark the tick against the correct answer in the following: 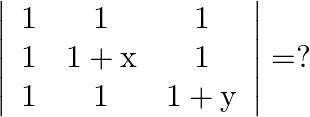
A. 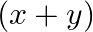
B. 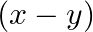
C. 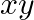
D. none of these
Solution: Option(C) To find: Value of $\left|\begin{array}{ccc}1 & 1 & 1 \\ 1 & 1+x & 1 \\ 1 & 1 & 1+y\end{array}\right|$ We have, $\left|\begin{array}{ccc}1 & 1 & 1...
Form the differential equation of the family of curves 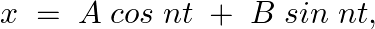 where
where  and
and  are arbitrary constants.
are arbitrary constants.
Equation of the family of curves, $x=A \cos n t+B \sin n t$, where $A$ and $B$ are arbitrary constants. Differentiating the above equation with respect to $t$ on both sides, we have,...
Mark the tick against the correct answer in the following: 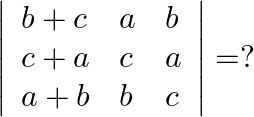
A. 
B. 
C. 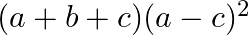
D. 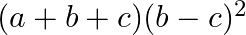
Solution: Option(C) To find: Value of $\left|\begin{array}{lll}b+c & a & b \\ c+a & c & a \\ a+b & b & c\end{array}\right|$ We have,...
If the plane 2x – 3y – 6z = 13 makes an angle 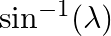 with the x-axis, then find the value of λ.
with the x-axis, then find the value of λ.
Answer: Direction ratios of the x-axis are 1,0,0 and direction ratios of normal to the plane are 2,−3,−6. The angle between the line and the plane,...
Find the vector equation of a line passing through the origin and perpendicular to the plane 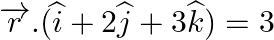
Answer:
Find the angle between the line 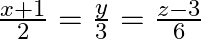 and the plane 10x + 2y – 11z = 3.
and the plane 10x + 2y – 11z = 3.
Answer: Direction ratios of the given line are 2,3,6 Direction ratios of the normal to the given plane are 10,2,−11 The angle between the line and the plane: \begin{array}{l} \sin...
Mark the tick against the correct answer in the following: 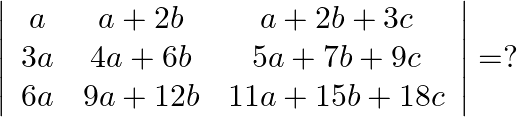
A. 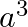
B. 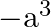
C. 0
D. none of these
Solution: Option(B) To find: Value of $\left|\begin{array}{ccc}a & a+2 b & a+2 b+3 c \\ 3 a & 4 a+6 b & 5 a+7 b+9 c \\ 6 a & 9 a+12 b & 11 a+15 b+18 c\end{array}\right|$ We...
Find the angle between the line 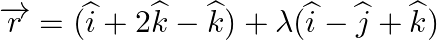 and the plane
and the plane 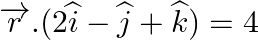
Answer: The equation of line is: $\vec{r}=(i+2 \hat{j}-\hat{k})+\lambda(\hat{i}-\hat{j}+\hat{k})$ Here, $\vec{b}=\hat{i}-j+\vec{k}$ The equation of plane is: r→·(2i^-j^+k^)=4 \vec{r}...
Find the angle between the line 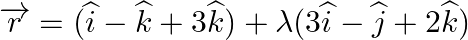 and the plane
and the plane 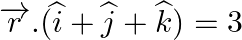
Answer: The equation of plane is: r→=(2i^-j^+3k^)+λ(3i^-j^+2k^) \vec{r}=(2 \hat{i}-\hat{j}+3 \hat{k})+\lambda(3 \hat{i}-\hat{j}+2 \hat{k}) On comparing with $\vec{r}=\vec{a}+\lambda...
Mark the tick against the correct answer in the following: 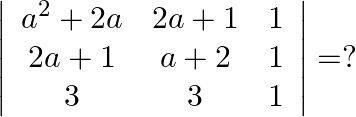
A. 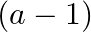
B. 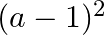
C. 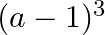
D. none of these
Solution: Option(C) To find: Value of $\left|\begin{array}{ccc}a^{2}+2 a & 2 a+1 & 1 \\ 2 a+1 & a+2 & 1 \\ 3 & 3 & 1\end{array}\right|$ We have,...
Find the value of m for which the line 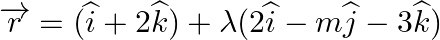 is parallel to the plane
is parallel to the plane 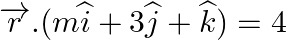
Answer: Given equation of line, $\overrightarrow r = (\widehat i + 2\widehat k) + \lambda (2\widehat i - m\widehat j - 3\widehat k)$ Comparing with the line $\overrightarrow r = \overrightarrow...
Form the differential equation of the family of circles in the second quadrant and touching the coordinate axes.
Equation of the family of circles in the second quadrant and touching the coordinate axes can be represented by $(x-(-a))^{2}+(y-a)^{2}=a^{2}$, where $a$ is an arbitrary constants....
Find the angle between the line joining the points A(3,−4,−2) and B(12,2,0) and the plane 3x−y+z=1.
Answer:
Show that the line line 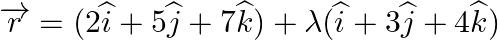 is parallel to the plane
is parallel to the plane 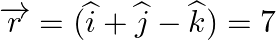 . Also, find the distance between them.
. Also, find the distance between them.
Answer: A line $\begin{array}{l} \overrightarrow r = \overrightarrow a + \lambda \overrightarrow b \\ \end{array}$ is parallel to the plane $\begin{array}{l} \overrightarrow r .\overrightarrow n ...
Mark the tick against the correct answer in the following: 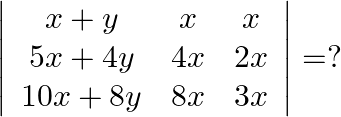
A. 0
B. 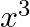
C. 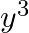
D. none of these
Solution: Option( B) To find: Value of $\left|\begin{array}{ccc}x+y & x & x \\ 5 x+4 y & 4 x & 2 x \\ 10 x+8 y & 8 x & 3 x\end{array}\right|$ We have,...
Find the angle between the line 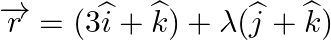 and the plane
and the plane 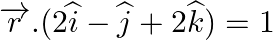
Answer: The equation of line is: r→=(3i^+k^)+λ(j^+k^) \vec{r}=(3 \hat{i}+\hat{k})+\lambda(\hat {j}+\hat{k}) Comparing with $\vec{r}=\vec{a}+\lambda \vec{b}$ $\vec{b}=(j+\dot{k})$. The...
Find the angle between the line ![Rendered by QuickLaTeX.com \[\frac{{x - 2}}{3} = \frac{{y + 1}}{{ - 1}} = \frac{{z - 3}}{{ - 2}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-24eba3255120c3288d2d203f342ddf45_l3.png)
and the plane 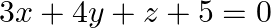
![Rendered by QuickLaTeX.com \[\frac{{x - 2}}{3} = \frac{{y + 1}}{{ - 1}} = \frac{{z - 3}}{{ - 2}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-24eba3255120c3288d2d203f342ddf45_l3.png)
Answer: The given line is $\frac{x-2}{3}=\frac{y+1}{-1}=\frac{2-3}{2}$ ⇒r→=(2i→-j→+k→)+t(3i→-j→-2k→) \Rightarrow...
Mark the tick against the correct answer in the following: If 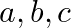 be distinct positive real numbers then the value of
be distinct positive real numbers then the value of 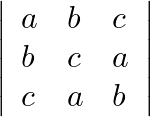 is
is
A. positive
B. negative
C. a perfect square
D. 0
Solution: Option(B) To find: Nature of $\left|\begin{array}{lll}a & b & c \\ b & c & a \\ c & a & b\end{array}\right|$ We have, $\left|\begin{array}{lll}a & b & c \\...
Mark the tick against the correct answer in the following: 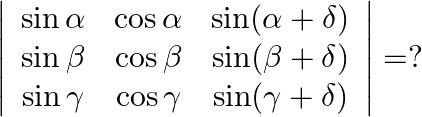
A. 0
B. 1
C. 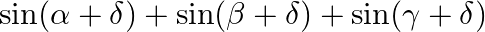
D. none of these
Solution: Option(A) To find: Value of $\left|\begin{array}{lll}\operatorname{sind} & \cos \alpha & \sin (\alpha+\bar{\delta}) \\ \sin \beta & \cos \beta & \sin (\beta+\bar{\delta})...
Form the differential equation of the family of curves, 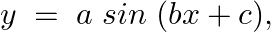 Where
Where  and
and 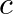 are parameters.
are parameters.
Equation of the family of curves, $y=a \sin (b x+c)$, Where $a$ and $c$ are parameters. Differentiating the above equation with respect to $x$ on both sides, we have, $\begin{array}{l} y=a \sin (b...
Mark the tick against the correct answer in the following: 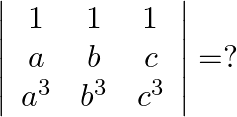
A. 
B. 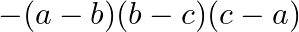
C. 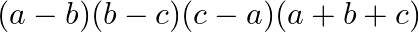
D. 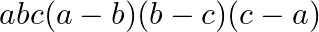
Solution: Option(C) To find: Value of $\left|\begin{array}{ccc}1 & 1 & 1 \\ a & b & c \\ a^{3} & b^{3} & c^{3}\end{array}\right|$ We have, $\left|\begin{array}{ccc}1 & 1...
Mark the tick against the correct answer in the following: 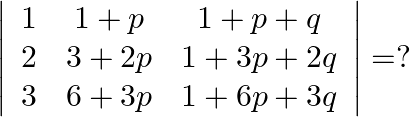
A. 0
B. 1
C. 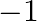
D. none of these
Solution: Option(B) To find: Value of $\left|\begin{array}{ccc}1 & 1+p & 1+p+q \\ 2 & 3+2 p & 1+3 p+2 q \\ 3 & 6+3 p & 1+6 p+3 q\end{array}\right|$ We have,...
Mark the tick against the correct answer in the following: 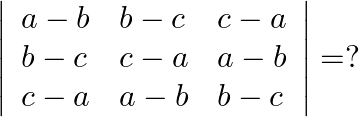
A. 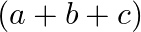
B. 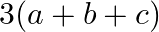
C. 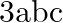
D. 0
Solution: Option(D) To find: Value of $\left|\begin{array}{lll}a-b & b-c & c-a \\ b-c & c-a & a-b \\ c-a & a-b & b-c\end{array}\right|$ We have, $\left|\begin{array}{lll}a-b...
Mark the tick against the correct answer in the following: 
A. 2
B. 6
C. 24
D. 120
Solution: Option(24) To find: Value of $\left|\begin{array}{lll}1 ! & 2 ! & 3 ! \\ 2 ! & 3 ! & 4 ! \\ 3 ! & 4 ! & 5 !\end{array}\right|$ We have,...
Mark the tick against the correct answer in the following: 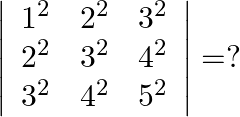
A. 8
B. 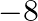
C. 16
D. 142
Solution: Option(A) To find: Value of $\left|\begin{array}{lll}1^{2} & 2^{2} & 3^{2} \\ 2^{2} & 3^{2} & 4^{2} \\ 3^{2} & 4^{2} & 5^{2}\end{array}\right|$ We have,...
Mark the tick against the correct answer in the following: If 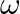 is a complex cube root of unity then the value of
is a complex cube root of unity then the value of 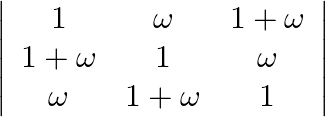 is
is
A. 2
B. 4
C. 0
D. 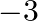
Solution: Option(0) To find: Value of $\left|\begin{array}{ccc}1 & \omega & 1+\omega \\ 1+\omega & 1 & \omega \\ \omega & 1+\omega & 1\end{array}\right|$ Formula used: (i)...
Mark the tick against the correct answer in the following: If 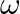 is a complex root of unity then
is a complex root of unity then 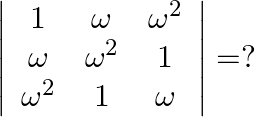
A. 1
B. 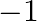
C. 0
D. none of these
Solution: Option(C) To find: Value of $\left|\begin{array}{ccc}1 & \omega & \omega^{2} \\ \omega & \omega^{2} & 1 \\ \omega^{2} & 1 & \omega\end{array}\right|$ We have,...
Mark the tick against the correct answer in the following: 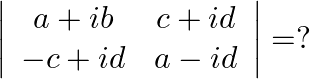
A. 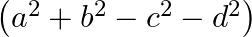
B. 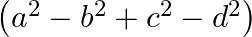
C. 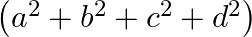
D. none of these
Solution: Option(C) To find: Value of $\left|\begin{array}{cc}a+i b & c+i d \\ -c+i d & a-i b\end{array}\right|$ Formula used: $\mathrm{i}^{2}=-1$ We have, $\left|\begin{array}{cc}a+i b...
Mark the tick against the correct answer in the following: 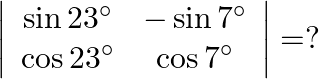
A. 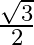
B. 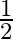
C. 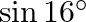
D. 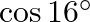
Solution: Option(B) To find: Value of $\left|\begin{array}{cc}\sin 23^{\circ} & -\sin 7^{\circ} \\ \cos 23^{\circ} & \cos 7^{\circ}\end{array}\right|$ Formula used: (i) $\sin (A+B)=\sin A...
Form the differential equation of the family of concentric circles x^{2} + y^{2}=a^{2}, where a>0 and a is a parameter.
X^2+y^2=a^2 Differentiating w.r.t x, 2x+2ydx/dy=0. Now as a is eliminated so this is the differential equation of the family of concentric circles. ⇒dx/dy=−y/x
Mark the tick against the correct answer in the following: 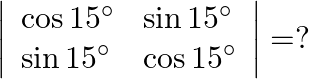
A. 1
B. 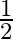
C. 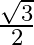
D. none of these
Solution: Option(C) To find: Value of $\left|\begin{array}{ll}\cos 15^{\circ} & \sin 15^{\circ} \\ \sin 15^{\circ} & \cos 15^{\circ}\end{array}\right|$ Formula used: (i) $\cos (A+B)=\cos A...
Mark the tick against the correct answer in the following: 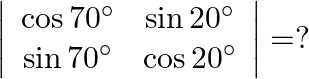
A. 1
B. 0
C. 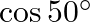
8D. 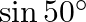
Solution: Option(B) To find: Value of $\left|\begin{array}{cc}\cos 70^{\circ} & \sin 20^{\circ} \\ \sin 70^{\circ} & \cos 20^{\circ}\end{array}\right|$ Formula used: (i) $\cos \theta=\sin...
Form the differential equation of the family of straight lines 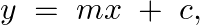 where
where 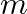 and
and 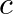 are arbitrary constants.
are arbitrary constants.
The equation of a straight line is represented as, $Y=m x+c$ Differentiating the above equation with respect to $x$, $\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{m}$ Differentiating the above equation...
As per the given question,