Answer: 1 ×10 1 = remainder obtained by dividing 1 × 1 by 10 = 1 3 ×10 7 = remainder obtained by dividing 3 × 7 by 10 = 1 7 ×10 9 = remainder obtained by dividing 7 × 9 by 10 = 3 Composition table:...
Construct the composition table for ×5 on set Z5 = {0, 1, 2, 3, 4}
Answer: 1 ×5 1 = remainder obtained by dividing 1 × 1 by 5 = 1 3 ×5 4 = remainder obtained by dividing 3 × 4 by 5 = 2 4 ×5 4 = remainder obtained by dividing 4 × 4 by 5 = 1 Composition table: ×5 0 1...
Construct the composition table for ×6 on set S = {0, 1, 2, 3, 4, 5}.
Answer: 1 ×6 1 = remainder obtained by dividing 1 × 1 by 6 = 1 3 ×6 4 = remainder obtained by dividing 3 × 4 by 6 = 0 4 ×6 5 = remainder obtained by dividing 4 × 5 by 6 = 2 Composition table: ×6 0 1...
Construct the composition table for +5 on set S = {0, 1, 2, 3, 4}
Answer: 1 +5 1 = remainder obtained by dividing 1 + 1 by 5 = 2 3 +5 1 = remainder obtained by dividing 3 + 1 by 5 = 2 4 +5 1 = remainder obtained by dividing 4 + 1 by 5 = 3 Composition Table: +5 0 1...
Construct the composition table for ×4 on set S = {0, 1, 2, 3}.
Answer: Given, ×4 on set S = {0, 1, 2, 3} 1 ×4 1 = remainder obtained by dividing 1 × 1 by 4 = 1 0 ×4 1 = remainder obtained by dividing 0 × 1 by 4 = 0 2 ×4 3 = remainder obtained by dividing 2 × 3...
Let * be a binary operation on Z defined by a * b = a + b – 4 for all a, b ∈ Z. (i) Show that * is both commutative and associative. (ii) Find the identity element in Z
Answers: (i) Consider, a, b ∈ Z a * b = a + b – 4 = b + a – 4 = b * a a * b = b * a, ∀ a, b ∈ Z Then, * is commutative on Z. a * (b * c) = a * (b + c – 4) = a + b + c -4 – 4 = a + b + c – 8 (a * b)...
Let * be a binary operation on Q0 (set of non-zero rational numbers) defined by a * b = (3ab/5) for all a, b ∈ Q0. Show that * is commutative as well as associative. Also, find its identity element, if it exists.
Answer: Consider, a, b ∈ Q0 a * b = (3ab/5) = (3ba/5) = b * a a * b = b * a, for all a, b ∈ Q0 a * (b * c) = a * (3bc/5) = [a (3 bc/5)] /5 = 3 abc/25 (a * b) * c = (3 ab/5) * c = [(3 ab/5)...
Let * be a binary operation on Q – {-1} defined by a * b = a + b + ab for all a, b ∈ Q – {-1}. Then, (i) Show that * is both commutative and associative on Q – {-1} (ii) Find the identity element in Q – {-1}
Answers: (i) Consider, a, b ∈ Q – {-1} a * b = a + b + ab = b + a + ba = b * a a * b = b * a, ∀ a, b ∈ Q – {-1} a * (b * c) = a * (b + c + b c) = a + (b + c + b c) + a (b + c + b c) = a + b +...
Let * be a binary operation on Q – {-1} defined by a * b = a + b + ab for all a, b ∈ Q – {-1}. Then, Show that every element of Q – {-1} is invertible. Also, find inverse of an arbitrary element.
Answer: Consider, a ∈ Q – {-1} and b ∈ Q – {-1} be the inverse of a. a * b = e = b * a a * b = e and b * a = e a + b + ab = 0 and b + a + ba = 0 b (1 + a) = – a Q – {-1} b = -a/1 + a Q – {-1}...
Let A = R0 × R, where R0 denote the set of all non-zero real numbers. A binary operation ‘O’ is defined on A as follows: (a, b) O (c, d) = (ac, bc + d) for all (a, b), (c, d) ∈ R0 × R. (i) Show that ‘O’ is commutative and associative on A (ii) Find the identity element in A
Answers: (i) Consider, X = (a, b) Y = (c, d) ∈ A, ∀ a, c ∈ R0 b, d ∈ R X O Y = (ac, bc + d) Y O X = (ca, da + b) X O Y = Y O X, ∀ X, Y ∈ A O is not commutative on A. X = (a, b) Y = (c, d) a Z = (e,...
Let A = R0 × R, where R0 denote the set of all non-zero real numbers. A binary operation ‘O’ is defined on A as follows: (a, b) O (c, d) = (ac, bc + d) for all (a, b), (c, d) ∈ R0 × R. Find the invertible element in A.
Answer: Consider, F = (m, n) be the inverse in A ∀ m ∈ R0 and n ∈ R X O F = E F O X = E (am, bm + n) = (1, 0) and (ma, na + b) = (1, 0) Considering (am, bm + n) = (1, 0) am = 1 m = 1/a And bm + n =...
Let * be a binary operation on Z defined by a * b = a + b – 4 for all a, b ∈ Z. Find the invertible element in Z.
Answer: Consider, a ∈ Z and b ∈ Z be the inverse of a. a * b = e = b * a a * b = e and b * a = e a + b – 4 = 4 and b + a – 4 = 4 b = 8 – a ∈ Z Hence, 8 – a is the inverse of a ∈...
Find the identity element in the set of all rational numbers except – 1 with respect to * defined by a * b = a + b + ab
Answer: Consider, e be the identity element in I+ with respect to * such that a * e = a = e * a, ∀ a ∈ Q – {-1} a * e = a and e * a = a, ∀ a ∈ Q – {-1} a + e + ae = a and e + a + ea = a, ∀ a ∈ Q –...
Find the identity element in the set I+ of all positive integers defined by a * b = a + b for all a, b ∈ I+.
Answer: Consider, e be the identity element in I+ with respect to * a * e = a = e * a, ∀ a ∈ I+ a * e = a and e * a = a, ∀ a ∈ I+ a + e = a and e + a = a, ∀ a ∈ I+ e = 0, ∀ a ∈ I+ Hence, 0 is the...
For the binary operation 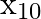 set
set 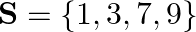 , find the inverse of 3 .
, find the inverse of 3 .
Solution: Here, $1 \times{ }_{10} 1=$ remainder obtained by dividing $1 \times 1$ by 10 $=1$ $3 \times{ }_{10} 7=$ remainder obtained by dividing $3 \times 7$ by 10 $=1$ $7 \times_{10} 9=$ remainder...
Construct the composition table for 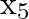 on set
on set 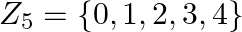
Solution: Here, $1 \times_{5} 1=$ remainder obtained by dividing $1 \times 1$ by 5 $=1$ $3 \times_{5} 4=$ remainder obtained by dividing $3 \times 4$ by 5 $=2$ $4 \times_{5} 4=$ remainder obtained...
Construct the composition table for 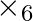 on set S = {0, 1, 2, 3, 4, 5}.
on set S = {0, 1, 2, 3, 4, 5}.
Solution: Here, $1 \times_{6} 1=$ remainder obtained by dividing $1 \times 1$ by 6 $=1$ $3 \times_{6} 4=$ remainder obtained by dividing $3 \times 4$ by 6 $=0$ $4 \times_{6} 5=$ remainder obtained...
Construct the composition table for 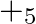 on set S = {0, 1, 2, 3, 4}
on set S = {0, 1, 2, 3, 4}
Solution: $1+_{5} 1=$ remainder obtained by dividing $1+1$ by 5 $=2$ $3+{ }_{5} 1=$ remainder obtained by dividing $3+1$ by 5 $=2$ $4+_{5} 1=$ remainder obtained by dividing $4+1$ by 5 $=3$...
Construct the composition table for 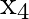 on set
on set 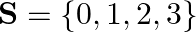 .
.
Solution: It is given that $x_{4}$ on set $S=\{0,1,2,3\}$ Here, $1 \times_{4} 1=$ remainder obtained by dividing $1 \times 1$ by 4 $=1$. $0 \times_{4} 1=$ remainder obtained by dividing $0 \times 1$...
Let 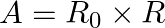 , where
, where 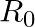 denote the set of all non-zero real numbers. A binary operation ‘O’ is defined on A as follows:
denote the set of all non-zero real numbers. A binary operation ‘O’ is defined on A as follows: 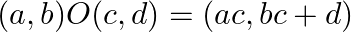 for all
for all 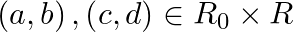 .(iii) Find the invertible element in A.
.(iii) Find the invertible element in A.
(iii) Assume $F=(m,n)$ be the inverse in $A\forall m\in {{R}_{0}}$and $n\in R$ $XOF=E$ and $FOX=E$ $(am,bm+n)=(1,0)$ and $(ma,na+b)=(1,0)$ Assuming $(am,bm+n)=(1,0)$ $am=1$ $m=1/a$ And $bm+n=0$...
Let 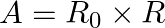 , where
, where 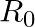 denote the set of all non-zero real numbers. A binary operation ‘O’ is defined on A as follows:
denote the set of all non-zero real numbers. A binary operation ‘O’ is defined on A as follows: 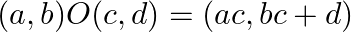 for all
for all 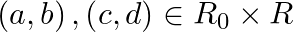 . (i) Show that ‘O’ is commutative and associative on A (ii) Find the identity element in A
. (i) Show that ‘O’ is commutative and associative on A (ii) Find the identity element in A
(i) Assume $X=(a,b)$ and $Y=(c,d)$$\in A,\forall a,c\in {{R}_{0}}$ and $b,d\in R$ Now, $XOY=(ac,bc+d)$ Then $YOX=(ca,da+b)$ So, $XOY=YOX,\forall X,Y\in A$ So, O is not commutative on A. Then we have...
Let * be a binary operation on  defined by
defined by 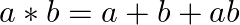 for all
for all 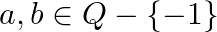 . Then(iii) Show that every element of
. Then(iii) Show that every element of  is invertible. Also, find inverse of an arbitrary element.
is invertible. Also, find inverse of an arbitrary element.
(iii) Assume $a\in Q-\left\{ -1 \right\}$ and $b\in Q-\left\{ -1 \right\}$ be the inverse of a. Then, $a*b=e=b*a$ $a*b=e$ and $b*a=e$ $a+b+ab=0$ and $b+a+ba=0$ $b(1+a)=–aQ–{-1}$ $b=-a/1+aQ–{-1}$...
. Let * be a binary operation on  defined by
defined by 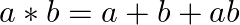 for all
for all 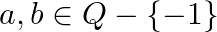 . Then, (i) Show that * is both commutative and associative on
. Then, (i) Show that * is both commutative and associative on  (ii) Find the identity element in
(ii) Find the identity element in 
(i) Firstly we all have to check commutativity of * Assume $a,b\in Q-\left\{ -1 \right\}$ So, $a*b=a+b+ab$ $=b+a+ba$ $=b*a$ Hence, $a*b=b*a$, $\forall a,b\in Q-\left\{ -1 \right\}$ Then we have to...
Let * be a binary operation on Q0 (set of non-zero rational numbers) defined by  for all
for all 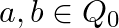 . Show that * is commutative as well as associative. Also, find its identity element, if it exists.
. Show that * is commutative as well as associative. Also, find its identity element, if it exists.
Firstly we all have to prove commutativity of * Assume $a,b\in {{Q}_{0}}$ $a*b=(3ab/5)$ $=(3ba/5)$ $=b*a$ Hence, $a*b=b*a$, for all $a,b\in {{Q}_{0}}$ Then we all have to prove associativity of *...
Let * be a binary operation on Z defined by 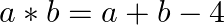 for all
for all 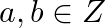 .(iii) Find the invertible element in Z.
.(iii) Find the invertible element in Z.
(iii) Assume $a\in Z$ and $b\in Z$ be the inverse of a. Now, $a*b=e=b*a$ $a*b=e$and $b*a=e$ $a+b–4=4$ and $b+a–4=4$ $b=8-a\in Z$ Therefore, $8–a$ is the inverse of $a\in Z$
Let * be a binary operation on Z defined by 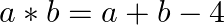 for all
for all 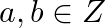 . (i) Show that * is both commutative and associative. (ii) Find the identity element in Z
. (i) Show that * is both commutative and associative. (ii) Find the identity element in Z
(i) Firstly we have to prove the commutatively of * Assume $a,b\in Z$. Now, $a*b=a+b–4$ $=b+a–4$ $=b*a$ Hence, $a*b=b*a,\forall a,b\in Z$ So, * is commutative on Z. Then, we all have to prove...
Find the identity element in the set of all rational numbers except 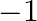 with respect to * defined by
with respect to * defined by 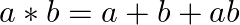
Assume ‘e’ be the identity element in ${{I}^{+}}$ with respect to * such that $a*e=a=e*a,\forall a\in Q-\left\{ -1 \right\}$ $a*e=a$and $e*a=a,\forall a\in Q-\left\{ -1 \right\}$ $a+e+ae=a$and...
Find the identity element in the set 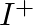 of all positive integers defined by
of all positive integers defined by 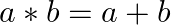 for all
for all 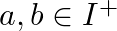 .
.
Assume ‘e’ be the identity element in ${{I}^{+}}$ with respect to * such that $a*e=a=e*a,\forall a\in {{I}^{+}}$ $a*e=a$and $e*a,\forall a\in {{I}^{+}}$ $a+e=a$ and $e+a=a$, $\forall a\in {{I}^{+}}$...
On the set Z of integers a binary operation * is defined by a 8 b = ab + 1 for all a, b ∈ Z. Prove that * is not associative on Z.
\[\begin{array}{*{35}{l}} Let\text{ }a,\text{ }b,\text{ }c\text{ }\in \text{ }Z \\ a\text{ }*\text{ }\left( b\text{ }*\text{ }c \right)\text{ }=\text{ }a\text{ }*\text{ }\left( bc\text{ }+\text{ }1...
Show that the binary operation * on Z defined by a * b = 3a + 7b is not commutative?
\[\begin{array}{*{35}{l}} Let\text{ }a,\text{ }b\text{ }\in \text{ }Z \\ a\text{ }*\text{ }b\text{ }=\text{ }3a\text{ }+\text{ }7b \\ b\text{ }*\text{ }a\text{ }=\text{ }3b\text{ }+\text{ }7a \\...
If the binary operation o is defined by a0b = a + b – ab on the set Q – {-1} of all rational numbers other than 1, show that o is commutative on Q – [1].
\[\begin{array}{*{35}{l}} Let\text{ }a,\text{ }b\text{ }\in \text{ }Q\text{ }\text{ }-\left\{ -1 \right\}. \\ Then\text{ }aob\text{ }=\text{ }a\text{ }+\text{ }b\text{ }-\text{ }ab \\ =\text{...
Check the commutativity and associativity of each of the following binary operations: (xv) ‘*’ on Q defined by a * b = gcd (a, b) for all a, b ∈ Q
(xv) to check: commutativity of * \[\begin{array}{*{35}{l}} Let\text{ }a,\text{ }b\text{ }\in \text{ }N,\text{ }then \\ a\text{ }*\text{ }b\text{ }=\text{ }gcd\text{ }\left( a,\text{ }b \right) ...
Check the commutativity and associativity of each of the following binary operations: (xiii) ‘*’ on Q defined by a * b = (ab/4) for all a, b ∈ Q (xiv) ‘*’ on Z defined by a * b = a + b – ab for all a, b ∈ Z
(xiii) to check :commutativity of * \[\begin{array}{*{35}{l}} Let\text{ }a,\text{ }b\text{ }\in \text{ }Q,\text{ }then \\ a\text{ }*\text{ }b\text{ }=\text{ }\left( ab/4 \right) \\ =\text{ }\left(...
Check the commutativity and associativity of each of the following binary operations: (xi) ‘*’ on N defined by a * b = ab for all a, b ∈ N (xii) ‘*’ on Z defined by a * b = a – b for all a, b ∈ Z
(xi) to check : commutativity of * \[\begin{array}{*{35}{l}} Let\text{ }a,\text{ }b\text{ }\in \text{ }N,\text{ }then \\ a\text{ }*\text{ }b\text{ }=\text{ }{{a}^{b}} \\ b\text{ }*\text{ }a\text{...
Check the commutativity and associativity of each of the following binary operations: (vii) ‘*’ on Q defined by a * b = a + a b for all a, b ∈ Q (viii) ‘*’ on R defined by a * b = a + b -7 for all a, b ∈ R
(vii) to check : commutativity of * \[\begin{array}{*{35}{l}} Let\text{ }a,\text{ }b\text{ }\in \text{ }Q,\text{ }then \\ a\text{ }*\text{ }b\text{ }=\text{ }a\text{ }+\text{ }ab \\ b\text{...
Check the commutativity and associativity of each of the following binary operations: (v) ‘o’ on Q defined by a o b = (ab/2) for all a, b ∈ Q (vi) ‘*’ on Q defined by a * b = ab2 for all a, b ∈ Q
(v) to check: commutativity of o \[\begin{array}{*{35}{l}} Let\text{ }a,\text{ }b\text{ }\in \text{ }Q,\text{ }then \\ a\text{ }o\text{ }b\text{ }=\text{ }\left( ab/2 \right) \\ =\text{ }\left(...
Check the commutativity and associativity of each of the following binary operations: (iii) ‘*’ on Q defined by a * b = a – b for all a, b ∈ Q (iv) ‘⊙’ on Q defined by a ⊙ b = a2 + b2 for all a, b ∈ Q
(iii) to check: commutativity of * \[\begin{array}{*{35}{l}} Let\text{ }a,\text{ }b\text{ }\in \text{ }Q,\text{ }then \\ a\text{ }*\text{ }b\text{ }=\text{ }a\text{ }-\text{ }b \\ b\text{...
Check the commutativity and associativity of each of the following binary operations: (i) ‘*’ on Z defined by a * b = a + b + a b for all a, b ∈ Z (ii) ‘*’ on N defined by a * b = 2ab for all a, b ∈ N
(i) to check: commutativity of * \[\begin{array}{*{35}{l}} Let\text{ }a,\text{ }b\text{ }\in \text{ }Z \\ =>\text{ }a\text{ }*\text{ }b\text{ }=\text{ }a\text{ }+\text{ }b\text{ }+\text{ }ab ...
Let A be any set containing more than one element. Let ‘*’ be a binary operation on A defined by a * b = b for all a, b ∈ A Is ‘*’ commutative or associative on A?
\[\begin{array}{*{35}{l}} Let\text{ }a,\text{ }b\text{ }\in \text{ }A \\ =>\text{ }a\text{ }*\text{ }b\text{ }=\text{ }b \\ b\text{ }*\text{ }a\text{ }=\text{ }a \\ Therefore\text{ }a\text{...
Determine which of the following binary operation is associative and which is commutative: (i) * on N defined by a * b = 1 for all a, b ∈ N (ii) * on Q defined by a * b = (a + b)/2 for all a, b ∈ Q
(i) to prove: commutativity of * Let \[\begin{array}{*{35}{l}} a,\text{ }b\text{ }\in \text{ }N \\ a\text{ }*\text{ }b\text{ }=\text{ }1 \\ b\text{ }*\text{ }a\text{ }=\text{ }1 \\ =>a\text{...
Let ‘*’ be a binary operation on N defined by a * b = l.c.m. (a, b) for all a, b ∈ N (i) Find 2 * 4, 3 * 5, 1 * 6. (ii) Check the commutativity and associativity of ‘*’ on N.
(i) Since, \[\begin{array}{*{35}{l}} a\text{ }*\text{ }b\text{ }=\text{ }1.c.m.\text{ }\left( a,\text{ }b \right) \\ 2\text{ }*\text{ }4\text{ }=\text{ }l.c.m.\text{ }\left( 2,\text{ }4 \right) \\...
Let S = {a, b, c}. Find the total number of binary operations on S.
Number of binary operations on a set with n elements is ${{n}^{{{n}^{2}}}}$ Here, S = {a, b, c} Number of elements in S = 3 Number of binary operations on a set with 3 elements is...
Is * defined on the set {1, 2, 3, 4, 5} by a * b = LCM of a and b a binary operation? Justify your answer.
LCM 1 2 3 4 5 1 1 2 3 4 5 2 2 2 6 4 10 3 3 5 3 12 15 4 4 4 12 4 20 5 5 10 15 20 5 Since,, all the elements are not in the set {1, 2, 3, 4, 5}. If we consider a = 2 and b = 3, a * b = LCM...
Let * be a binary operation on the set I of integers, defined by a * b = 2a + b − 3. Find the value of 3 * 4.
\[\begin{array}{*{35}{l}} a~*~b~=\text{ }2a~+~b~-\text{ }3 \\ 3\text{ }*\text{ }4\text{ }=\text{ }2\text{ }\left( 3 \right)\text{ }+\text{ }4\text{ }-\text{ }3 \\ =\text{ }6\text{ }+\text{...
Determine whether or not the definition of * given below gives a binary operation. In the event that * is not a binary operation give justification of this.(v) On Z+ define * by a * b = a (vi) On R, define * by a * b = a + 4b2
(v) Given on Z+ define * by a * b = a Let \[\begin{array}{*{35}{l}} a,\text{ }b\text{ }\in \text{ }{{Z}^{+}} \\ \Rightarrow \text{ }a\text{ }\in \text{ }{{Z}^{+}} \\ \Rightarrow \text{ }a\text{...
Determine whether or not the definition of * given below gives a binary operation. In the event that * is not a binary operation give justification of this.(iii) On R, define * by a*b = ab2 (iv) On Z+ define * by a * b = |a − b|
(iii) Since, on R, define by a*b = ab2 Let \[\begin{array}{*{35}{l}} a,\text{ }b\text{ }\in \text{ }R \\ \Rightarrow \text{ }a,\text{ }{{b}^{2}}~\in \text{ }R \\ \Rightarrow \text{ }a{{b}^{2}}~\in...
Determine whether or not the definition of * given below gives a binary operation. In the event that * is not a binary operation give justification of this. (i) On Z+, defined * by a * b = a – b (ii) On Z+, define * by a*b = ab
(i)Since, On Z+, defined * by a * b = a – b If a = 1 and b = 2 in Z+, then \[\begin{array}{*{35}{l}} a\text{ }*\text{ }b\text{ }=\text{ }a\text{ }-\text{ }b \\ =\text{ }1\text{ }-\text{ }2 \\...
Determine whether the following operation define a binary operation on the given set or not:(vii) ‘*’ on Q defined by a * b = (a – 1)/ (b + 1) for all a, b ∈ Q
(vii)Since, ‘*’ on Q defined by a * b = (a – 1)/ (b + 1) for all a, b ∈ Q If a = 2 and b = -1 in Q, \[\begin{array}{*{35}{l}} a\text{ }*\text{ }b\text{ }=\text{ }\left( a\text{ }-\text{ }1...
Determine whether the following operation define a binary operation on the given set or not: (v) ‘+6’ on S = {0, 1, 2, 3, 4, 5} defined by a +6 b ![Rendered by QuickLaTeX.com \[\{_{a+b-6;ifa+b\ge 6}^{a+b;ifa+b<6}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-9b727b75dbf6654367aa63ceb06884f2_l3.png)
(vi) ‘⊙’ on N defined by a ⊙ b= ab + ba for all a, b ∈ N
(v) Given ‘+6’ on S = {0, 1, 2, 3, 4, 5} defined by a +6 b Consider the composition table, +6 0 1 2 3 4 5 0 0 1 2 3 4 5 1 1 2 3 4 5 0 2 2 3 4 5 0 1 3 3 4 5 0 1 2 4 4 5 0 1 2 3 5 5 0 1 2 3 4 Here all...
Determine whether the following operation define a binary operation on the given set or not: (iii) ‘*’ on N defined by a * b = a + b – 2 for all a, b ∈ N (iv) ‘×6‘ on S = {1, 2, 3, 4, 5} defined by a ×6 b = Remainder when a b is divided by 6.
(iii) Given ‘*’ on N defined by a * b = a + b – 2 for all a, b ∈ N \[\begin{array}{*{35}{l}} If~a~=\text{ }1\text{ }and~b\text{ }=\text{ }1, \\ a\text{ }*\text{ }b\text{ }=\text{ }a\text{ }+\text{...
Determine whether the following operation define a binary operation on the given set or not: (i) ‘*’ on N defined by a * b = ab for all a, b ∈ N. (ii) ‘O’ on Z defined by a O b = ab for all a, b ∈ Z.
(i) Given ‘*’ on N defined by a * b = ab for all a, b ∈ N. Let a, b ∈ N. Then, \[\begin{array}{*{35}{l}} {{a}^{b~}}\in ~N~~~~~~\left[ \because ~{{a}^{b}}\ne 0~and~a,\text{ }b~is~positive~integer...
