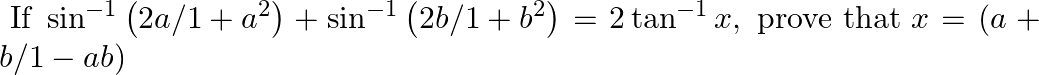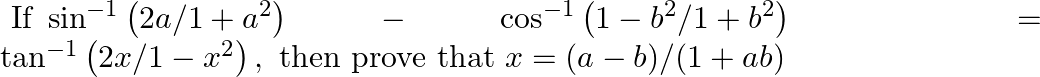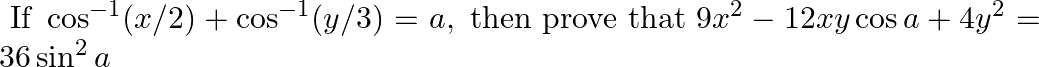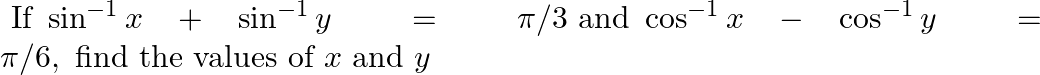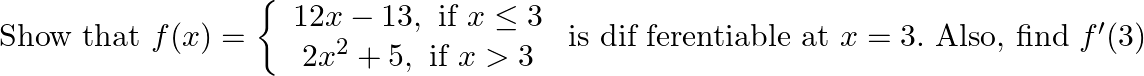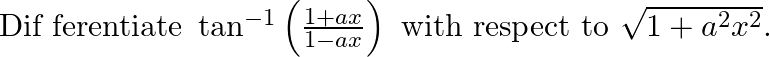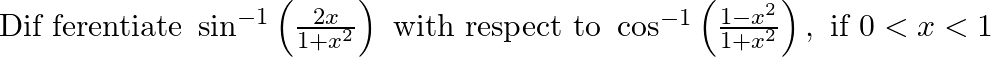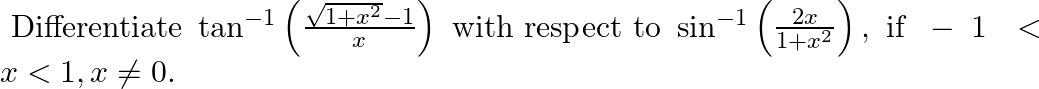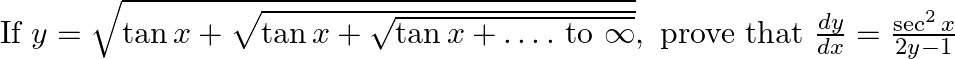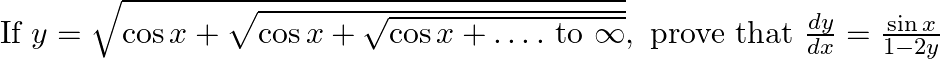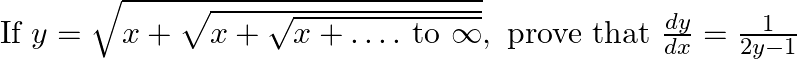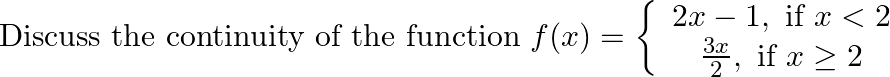Given sin-1 (2a/ 1+ a2) + sin-1 (2b/ 1+ b2) = 2 tan-1 x
Prove that: (i) 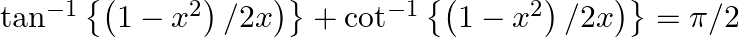 (ii)
(ii) 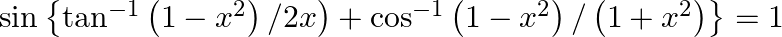
$(i)$ $(ii)$
Prove the following results: (ix) 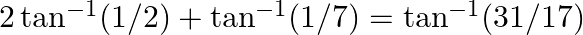 (x)
(x) 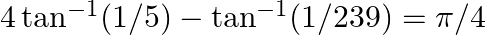
$(ix)$ $(x)$
Prove the following results: (vii) 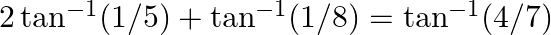 (viii)
(viii) 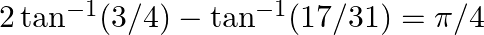
$(vii)$ $(viii)$
Prove the following results: (v) 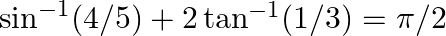 (vi)
(vi) 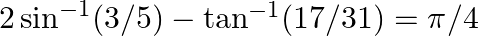
$(v)$ $(vi)$
Prove the following results: (iii) 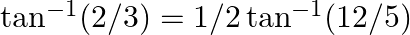 (iv)
(iv) 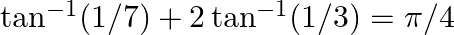
$(iii)$ $(iv)$
Prove the following results: (i) 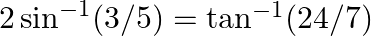 (ii)
(ii) 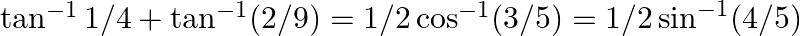
$(i)$ $(ii)$
Evaluate the following: (iii) 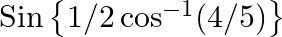 (iv)
(iv) 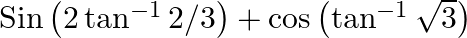
$(iii)$ $(iv)$
Evaluate the following: (i) 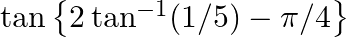 (ii)
(ii) 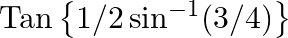
$(i)$ $(ii)$
Since, cos-1 (a/x) – cos-1 (b/x) = cos-1 (1/b) – cos-1 (1/a)
Given Cos (sin -1 3/5 + sin-1 5/13)
Prove the following results: (iii) 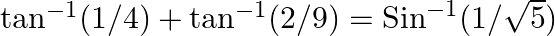
$(iii)$
Prove the following results: (i) 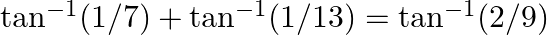 (ii)
(ii) 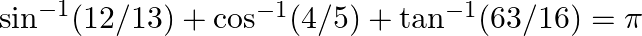
$(i)$ $(ii)$ LHS
If 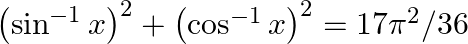 , find
, find 
Since, $\cos ^{-1} x+\sin ^{-1} x=\pi / 2$ => $\cos ^{-1} x=\pi / 2-\sin ^{-1} x$ Substituting this in $\left(\sin ^{-1} x\right)^{2}+\left(\cos ^{-1} x\right)^{2}=17 \pi^{2} / 36$ $\left(\sin...
$\cot \left(\cos ^{-1} 3 / 5+\sin ^{-1} x\right)=0$ => $\begin{array}{l} \left(\cos ^{-1} 3 / 5+\sin ^{-1} x\right)=\cot ^{-1}(0) \\ \left(\operatorname{Cos}^{-1} 3 / 5+\sin ^{-1} x\right)=\pi /...
Given sin-1 x + sin-1 y = π/3 ……. (i) And cos-1 x – cos-1 y = π/6 ……… (ii)
Since, cos-1 x + cos-1 y = π/4
Evaluate: (v) 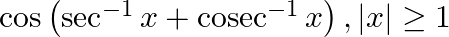
$(v)$ $=>0$
Evaluate: (iii) 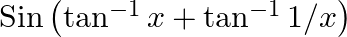 for
for 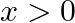 (iv) Cot
(iv) Cot 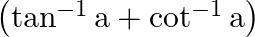
$(iii)$ $(iv)$
Evaluate: (i) 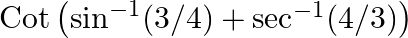 (ii)
(ii) 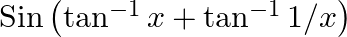 for
for 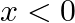
$(i)$ $(ii)$
Evaluate: (iii) cot 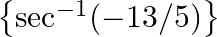
$(iii)$
Evaluate: (i) 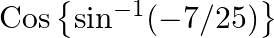 (ii) Sec
(ii) Sec 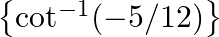
$(i)$ $(ii)$
Evaluate each of the following: (ix) 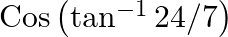
$(ix)$ .
Evaluate each of the following: (vii) Tan 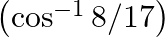 (viii)
(viii) 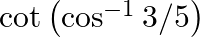
$(vii)$ $(viii)$
Evaluate each of the following: (v) 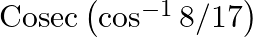 (vi)
(vi) 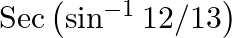
(v) \[\begin{array}{*{35}{l}} {} \\ Let\text{ }co{{s}^{-1}}\left( 8/17 \right)\text{ }=\text{ }y \\ cos\text{ }y\text{ }=\text{ }8/17\text{ }where\text{ }y\text{ }\in \text{ }\left[ 0,\text{ }\pi...
Evaluate each of the following: (iii) 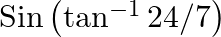 (iv)
(iv) 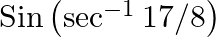
(iii) (iv)
Evaluate each of the following: (i) 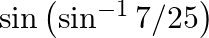 (ii)
(ii) 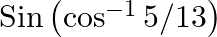
(i) \[\begin{array}{*{35}{l}} Given\text{ }sin\text{ }\left( si{{n}^{-1}}~7/25 \right) \\ let\text{ }y\text{ }=\text{ }si{{n}^{-1}}~7/25 \\ sin\text{ }y\text{ }=\text{ }7/25\text{ }where\text{...
Find the derivative of the function f defined by f (x) = mx + c at x = 0.
f(x) = mx + c, Checking the differentiability at x = 0 This is the derivative of a function at x = 0, and also this is the derivative of this function at every value of x.
If f (x) =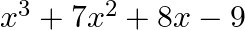 , find f’ (4).
, find f’ (4).
f(x) = x3 + 7x2 + 8x – 9, => Checking the differentiability at x = 4
If for the function Ø (x) =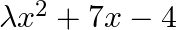 , Ø’ (5) = 97, find λ.
, Ø’ (5) = 97, find λ.
Finding the value of λ given in the real function and we are given with the differentiability of the function f(x) = λx2 + 7x – 4 at x = 5 which is f ‘(5) = 97 =>
Show that the derivative of the function f is given by f (x) = ![Rendered by QuickLaTeX.com \[~\mathbf{2}{{\mathbf{x}}^{\mathbf{3}}}~\text{ }\mathbf{9}{{\mathbf{x}}^{\mathbf{2}~}}+\text{ }\mathbf{12}\text{ }\mathbf{x}\text{ }+\text{ }\mathbf{9}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c388eec2224700cda456bd12406ee5c9_l3.png)
, at x = 1 and x = 2 are equal.
We are given with a polynomial function f(x) = 2x3 – 9x2 + 12x + 9, and we have
If f is defined by f (x) = 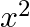 – 4x + 7, show that f’ (5) = 2 f’ (7/2)
– 4x + 7, show that f’ (5) = 2 f’ (7/2)
Discuss the continuity and differentiability of the function f (x) = |x| + |x -1| in the interval of (-1, 2).
Since, a polynomial and a constant function is continuous and differentiable everywhere => f(x) is continuous and differentiable for x ∈ (-1, 0) and x ∈ (0, 1) and (1, 2). Checking continuity...
Show that the function  is defined as follows
is defined as follows 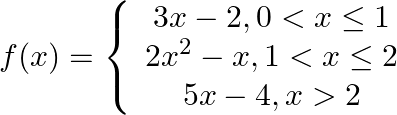 Is continuous at
Is continuous at 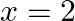 , but not differentiable thereat.
, but not differentiable thereat.
Since, LHL = RHL = f (2) Hence, F(x) is continuous at x = 2 Checking the differentiability at x = 2 $=> 5$ Since, (RHD at x = 2) ≠ (LHD at x = 2) Hence, f (2) is not differentiable at x =...
checking differentiability of given function at x = 3 => LHD (at x = 3) = RHD (at x = 3) = 12 Since, (LHD at x = 3) = (RHD at x = 3) Hence, f(x) is differentiable at x = 3.
Show that f (x) =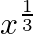 is not differentiable at x = 0.
is not differentiable at x = 0.
Since, LHD and RHD does not exist at x = 0 Hence, f(x) is not differentiable at x = 0
Show that f (x) = |x – 3| is continuous but not differentiable at x = 3.
Differentiate 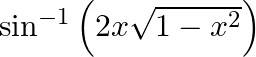 with respect to
with respect to 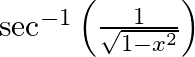 , if, (i)
, if, (i) 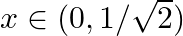 (ii)
(ii) 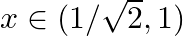
(i) Let (ii) Let
Differentiate 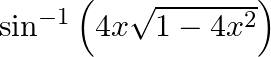 with respect to
with respect to 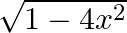 if, (iii)
if, (iii) 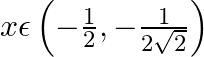
(iii) Let
Differentiate 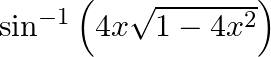 with respect to
with respect to 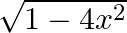 if, (i)
if, (i) 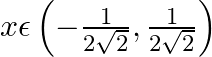 (ii)
(ii) 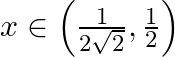
(i) Let (ii)
Differentiate 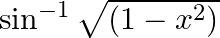 with respect to
with respect to 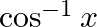 , if (i)
, if (i) 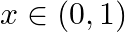 (ii)
(ii) 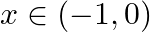
(i) Given sin-1 √ (1-x2) (ii) Given sin-1 √ (1-x2)
If 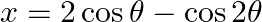 and
and 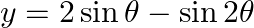 , prove that
, prove that 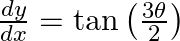 .
.
Find dy/dx, when 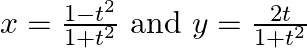
Find dy/dx, when 
Find dy/dx, when x = 2 t / 1+t^2 and y = 1-t^2 / 1+t^2.
Given, $x=2 t /\left(1+t^{2}\right)$ On differentiating $x$ with respect to t using quotient rule, $$ \begin{array}{l} \frac{\mathrm{dx}}{\mathrm{dt}}=\left[\frac{\left(1+\mathrm{t}^{2}\right)...
Find dy/dx, when 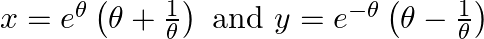
Find dy/dx, when 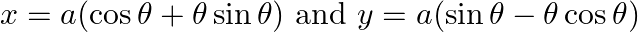
Find dy/dx, when x = 3 a t / 1+t^2 and y = 3 a t^2/1+t^2
Find dy/dx, when 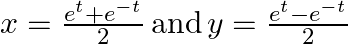
Find dy/dx, when 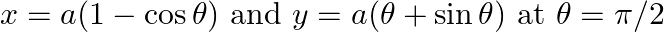
Find dy/dx, when 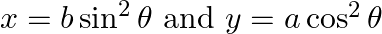
Find dy/dx, when 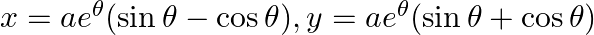
Find dy/dx, when 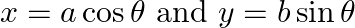
Find dy/dx, when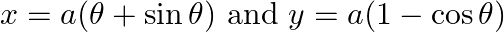
Find dy/dx, when 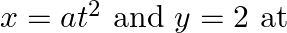
Differentiate the following functions with respect to x: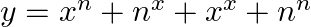
Differentiate the following functions with respect to x: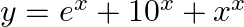
(vii) (viii)
Differentiate the following functions with respect to x: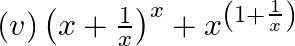
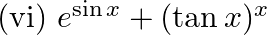
(v) (vi)
Differentiate the following functions with respect to x: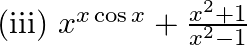
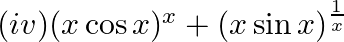
(iv)
Differentiate the following functions with respect to x: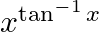
Differentiate the following functions with respect to x: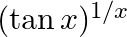
Differentiate the following functions with respect to x: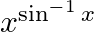
Differentiate the following functions with respect to x: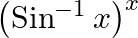
Differentiate the following functions with respect to x: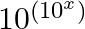
Differentiate the following functions with respect to x: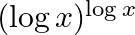
Differentiate the following functions with respect to x: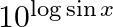
Differentiate the following functions with respect to x: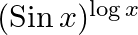
Differentiate the following functions with respect to x: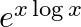
Differentiate the following functions with respect to x: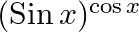
Differentiate the following functions with respect to x: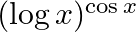
Let y = (log x)cos x Taking log both the sides, we get
Differentiate the following functions with respect to x: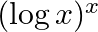
Differentiate the following functions with respect to x: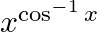
Differentiate the following functions with respect to x: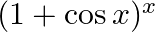
Differentiate the following functions with respect to x: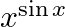
Differentiate the following functions with respect to x: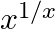
If 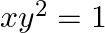 , prove that
, prove that 
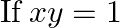 , prove that
, prove that 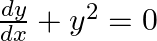 .
.
If 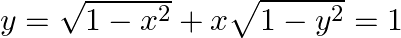 , prove that
, prove that 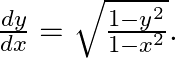
If 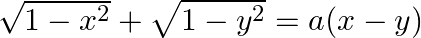 , prove that
, prove that 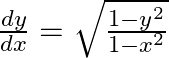
Find dy/dx in each of the following: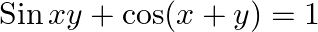
differentiating the equation on both sides with respect to x, we get,
Find dy/dx in each of the following: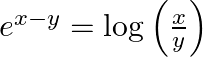
Find dy/dx in each of the following: 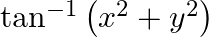
differentiating the equation on both sides with respect to x, we get,
Find dy/dx in each of the following: 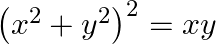
differentiating the equation on both sides with respect to x, we get,
Find dy/dx in each of the following: 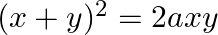
differentiating the equation on both sides with respect to x, we get,
Find dy/dx in each of the following: 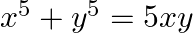
differentiating the equation on both sides with respect to x, we get,
Find dy/dx in each of the following: 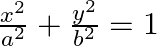
Find dy/dx in each of the following: 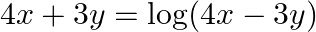
differentiating the equation on both sides with respect to x, we get,
Find dy/dx in each of the following: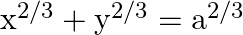
differentiating the equation on both sides with respect to x, we get,
Find dy/dx in each of the following: 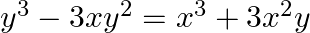
differentiating the equation on both sides with respect to x, we get,
Find dy/dx in each of the following: 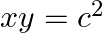
Differentiate the following functions with respect to x: 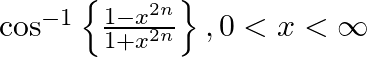
Differentiate the following functions with respect to x: 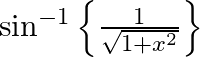
Differentiate the following functions with respect to x: 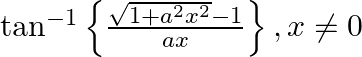
Differentiate the following functions with respect to x: 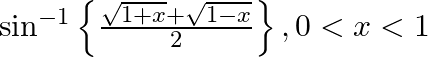
Differentiate the following functions with respect to x: 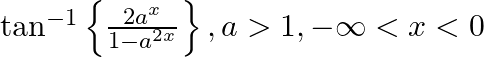
Differentiate the following functions with respect to x: 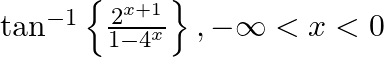
Differentiate the following functions with respect to x: 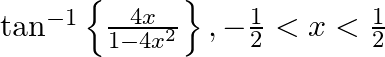
Differentiate the following functions with respect to x: 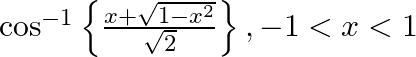
Differentiate the following functions with respect to x: 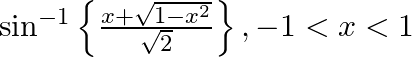
Differentiate the following functions with respect to x: 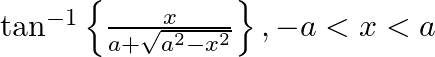
Differentiate the following functions with respect to x: 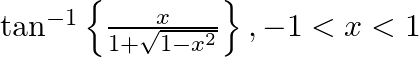
Differentiate the following functions with respect to x: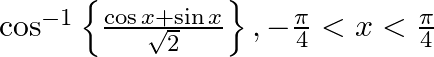
Differentiate the following functions with respect to x: 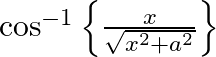
Differentiate the following functions with respect to x: 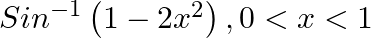
Differentiate the following functions with respect to x: 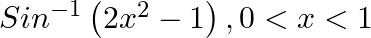
Differentiate the following functions with respect to x: 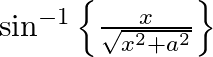
Differentiate the following functions with respect to x: 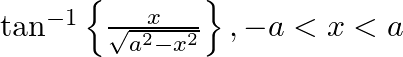
Differentiate the following functions with respect to x: 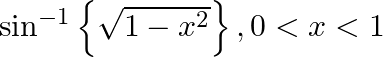
Let,
Differentiate the following functions with respect to x: 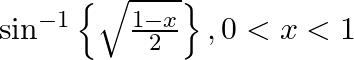
Let,
Differentiate the following functions with respect to x: 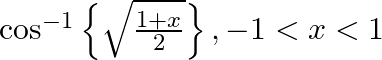
Differentiate the following functions with respect to x: 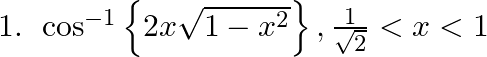
Differentiate the following functions with respect to x: 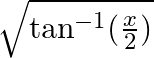
Differentiate the following functions with respect to x: 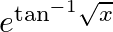
Differentiate the following functions with respect to x: 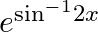
Differentiate the following functions with respect to x: 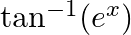
Differentiate the following functions with respect to x: 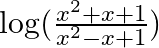
Differentiate the following functions with respect to x: 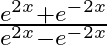
Differentiate the following functions with respect to x: log (cosec x – cot x)
Differentiate the following functions with respect to x: 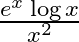
Differentiate the following functions with respect to x: 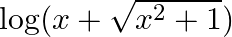
Differentiate the following functions with respect to x: x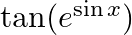
Differentiate the following functions with respect to x: 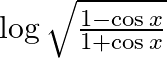
Differentiate the following functions with respect to x: 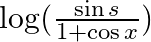
Differentiate the following functions with respect to x: 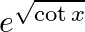
Differentiate the following functions with respect to x: 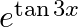
Differentiate the following functions with respect to x: 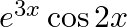
Differentiate the following functions with respect to x: 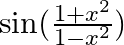
Differentiate the following functions with respect to x: 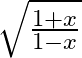
Differentiate the following functions with respect to x: 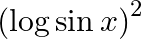 .
.
Let y = (log sin x)2
Differentiate the following functions with respect to x: 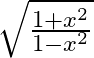
Differentiate the following functions with respect to x: 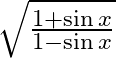
Differentiate the following functions with respect to x: 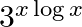
Differentiate the following functions with respect to x: 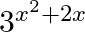
Differentiate the following functions with respect to x: ![Rendered by QuickLaTeX.com \[\mathbf{lo}{{\mathbf{g}}_{\mathbf{x}}}~\mathbf{3}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-ff5c2c46f9e67b0239c75b89cbf3a0a4_l3.png)
Differentiate the following functions with respect to x: 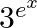
Differentiate the following functions with respect to x: 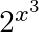
Differentiate the following functions with respect to x: tan 5x
Let y = tan (5x°)
Differentiate the following functions with respect to x: ![Rendered by QuickLaTeX.com \[\mathbf{lo}{{\mathbf{g}}_{\mathbf{7}}}~\left( \mathbf{2x}\text{ }\text{ }\mathbf{3} \right)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-9548ffb8700a3c7168d42bef1698dab2_l3.png)
Differentiate the following functions with respect to x: ![Rendered by QuickLaTeX.com \[~\mathbf{Si}{{\mathbf{n}}^{\mathbf{2}}}~\left( \mathbf{2x}\text{ }+\text{ }\mathbf{1} \right)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b40c28b7926d22db3057d590b6cc73ca_l3.png)
Let y = sin2 (2x + 1) On differentiating y with respect to x, we get
Differentiate the following functions with respect to x: 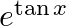
Differentiate the following functions with respect to x: 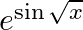
Differentiate the following functions with respect to x: Sin (log x)
Differentiate the following functions with respect to x: ![Rendered by QuickLaTeX.com \[\mathbf{tan}\text{ }({{\mathbf{x}}^{\mathbf{o}}}~+\text{ }\mathbf{4}{{\mathbf{5}}^{\mathbf{o}}})\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-464d3400e1e5d6359b79f09c8ce8e182_l3.png)
Differentiate the following functions with respect to x: 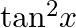
Given tan2 x
Differentiate the following functions from the first principles: 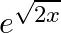
Differentiate the following functions from the first principles: 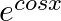
let f (x) = ecos x By using the first principle formula, we get,
Differentiate the following functions from the first principles: 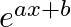
Differentiate the following functions from the first principles: 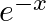
A real function f is said to be continuous at x = c, where c is any point in the domain of f if A function is continuous at x = c if Function is changing its nature (or expression) at x = 2, so we...
If 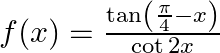 for
for 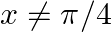 , find the value which can be assigned to
, find the value which can be assigned to 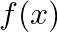 at
at 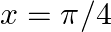 so that the function
so that the function 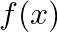 becomes continuous everywhere in
becomes continuous everywhere in ![Rendered by QuickLaTeX.com [0, \pi / 2]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b8bf04cd2ca4b4771433b6b0371ba22f_l3.png) .
.
A real function f is said to be continuous at x = c, where c is any point in the domain of f if Where h is a very small positive number. i.e. left hand limit as x → c (LHL) = right hand limit as...
The function 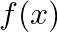 is defined by
is defined by 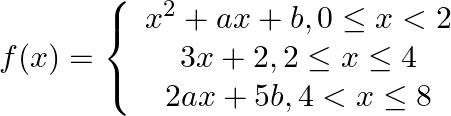 If f is continuous on [0, 8], find the values of a and b.
If f is continuous on [0, 8], find the values of a and b.
A real function f is said to be continuous at x = c, where c is any point in the domain of f if h is a very small positive number. i.e. left hand limit as x → c (LHL) = right hand limit as x → c...
Find the values of a and b so that the function f (x) defined by 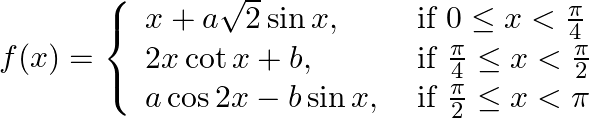
The function 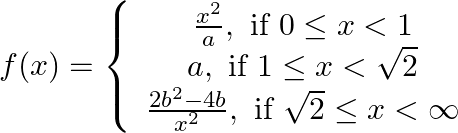 Is continuous on
Is continuous on 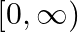 . Find the most suitable values of
. Find the most suitable values of 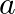 and
and 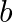 .
.
A real function f is said to be continuous at x = c, where c is any point in the domain of f if h is a very small positive number. i.e. left hand limit as x → c (LHL) = right hand limit as x → c...
In the following, determine the value(s) of constant(s) involved in the definition so that the given function is continuous: (iii) 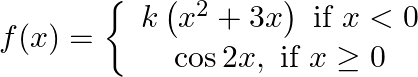 (i v)
(i v) 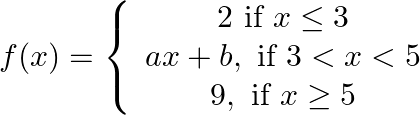
(iii) A real function f is said to be continuous at x = c, where c is any point in the domain of f if h is a very small positive number. i.e. left hand limit as x → c (LHL) = right hand limit as x →...
In the following, determine the value(s) of constant(s) involved in the definition so that the given function is continuous: (i) 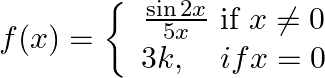 (ii)
(ii) 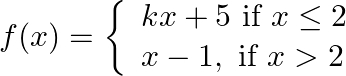
(i) A real function f is said to be continuous at x = c, where c is any point in the domain of f if h is a very small positive number. i.e. left hand limit as x → c (LHL) = right hand limit as x → c...
Find the points of discontinuity, if any, of the following functions: (x i) 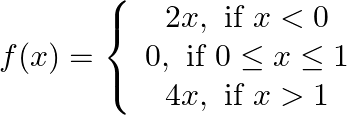 (x i i)
(x i i) 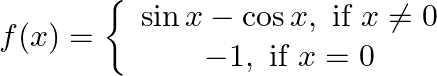
(xi) A real function f is said to be continuous at x = c, where c is any point in the domain of f if h is a very small positive number. i.e. left hand limit as x → c (LHL) = right hand limit as x →...
Find the points of discontinuity, if any, of the following functions: (i x) 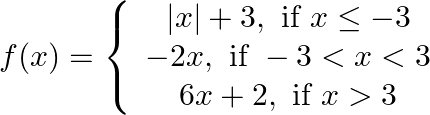 (x)
(x) 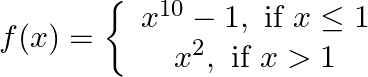
(ix) A real function f is said to be continuous at x = c, where c is any point in the domain of f if h is a very small positive number. i.e. left hand limit as x → c (LHL) = right hand limit as x →...
Find the points of discontinuity, if any, of the following functions: 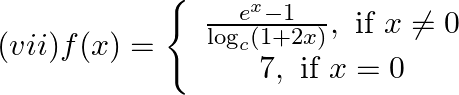 (viii)
(viii) 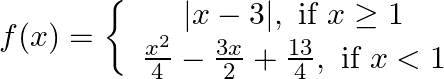
((vii) A real function f is said to be continuous at x = c, where c is any point in the domain of f if h is a very small positive number. i.e. left hand limit as x → c (LHL) = right hand limit as x...
Find the points of discontinuity, if any, of the following functions: (i) 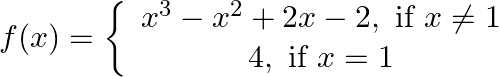 (ii)
(ii) 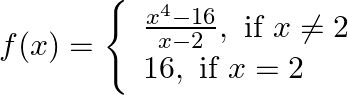
(i) A real function f is said to be continuous at x = c, where c is any point in the domain of f if h is a very small positive number. i.e. left hand limit as x → c (LHL) = right hand limit as x → c...
Discuss the the continuity of the function 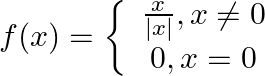
A real function f is said to be continuous at x = c, where c is any point in the domain of f if Since, h is a very small positive number. i.e. left hand limit as x → c (LHL) = right hand limit as x...
Prove that the function 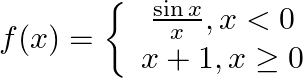 is everywhere continuous.
is everywhere continuous.
A real function f is said to be continuous at x = c, where c is any point in the domain of f if A function is continuous at x = c if From definition of f(x), f(x) is defined for all real numbers....
Find the inverse of the following matrices by using elementary row transformations: ![Rendered by QuickLaTeX.com \left[\begin{array}{cc}7 & 1 \\ 4 & -3\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2c36dc19722d96911b3cd4f2fe953983_l3.png)
Solution: For row transformation $\begin{array}{l} A=I A \\ \Rightarrow\left[\begin{array}{cc} 7 & 1 \\ 4 & -3 \end{array}\right]=\left[\begin{array}{ll} 1 & 0 \\ 0 & 1...
43.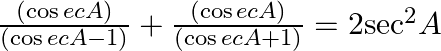
Assuming the L.H.S and taking L.C.M and on simplifying we will get, $=\frac{(\cos ecA)(\cos ecA+1+\cos ecA-1)}{(\cos e{{c}^{2}}A-1)}$ $=\frac{(2\cos e{{c}^{2}}A)}{{{\cot }^{2}}A}$ $=\frac{2{{\sin...
42.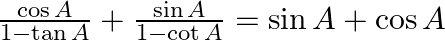
Solving the L.H.S, we will get $=\frac{\cos A}{1-\tan A}+\frac{\sin A}{1-\cot A}$ $=\frac{\cos A}{1-\frac{\sin A}{\cos A}}+\frac{\sin A}{1-\frac{\cos A}{\sin A}}$ $=\frac{{{\cos }^{2}}A}{\cos A-\sin...
41.
Assuming L.H.S and taking L.C.M and on simplifying we will get, $=\frac{\sec A+1+\sec A-1}{(\sec A+1)(\sec A-1)}$ $=\frac{2\sec A}{({{\sec }^{2}}A-1)}$ $=\frac{2{{\cos }^{2}}A}{(\cos A{{\sin...
40. 
Solving L.H.S and divide the numerator and denominator with $(1-\cos A),$, we have $=\frac{(1-\cos A)(1-\cos A)}{(1+\cos A)(1-\cos A)}$ $=\frac{{{(1-\cos A)}^{2}}}{(1+{{\cos }^{2}}A)}$...
39.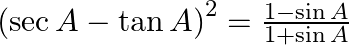
Solving $LHS={{(\sec A-\tan A)}^{2}}$, we get $={{\left[ \frac{1}{\cos A}-\frac{\sin A}{\cos A} \right]}^{2}}$ $=\frac{{{(1-\sin A)}^{2}}}{{{\cos }^{2}}A}$ $=\frac{{{(1-\sin A)}^{2}}}{1-{{\sin...
38. Prove that:(iii)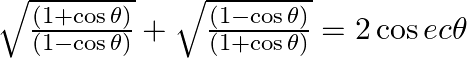 (iv)
(iv) 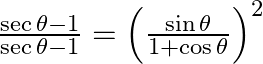
Solving L.H.S and dividing the numerator and denominator with its respective conjugates, we have $=\sqrt{\frac{(1-\cos \theta )(1-\cos \theta )}{(1+\cos \theta )(1-\cos \theta...
38. Prove that: (i)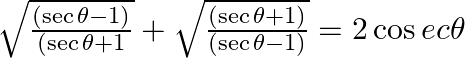 (ii)
(ii)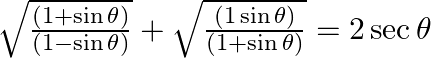
Solving L.H.S and divide the numerator and denominator with its respective conjugates, we have $=\sqrt{\frac{(\sec \theta -1)(\sec \theta -1)}{(\sec \theta +1)(\sec \theta -1)}}+\sqrt{\frac{(\sec...
37. (i) 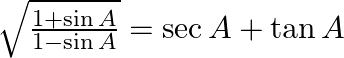 (ii)
(ii)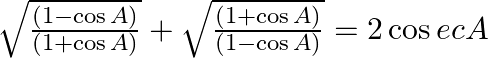
Solving L.H.S and dividing the numerator and denominator with $\sqrt{(1+\sin A)},$we have $=\sqrt{\frac{(1+\sin A)(1+\sin A)}{(1-\sin A)(1+\sin A)}}=\sqrt{\frac{{{(1+\sin A)}^{2}}}{1-{{\sin...
36.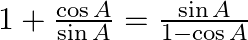
Solving L.H.S $LHS=\frac{1+\cos A}{\sin A}$ Multiply the numerator and denominator by $(1-\cos A)$ we will have $=\frac{(1+\cos A)(1-\cos A)}{\sin A(1-\cos A)}$ $=\frac{1-{{\cos }^{2}}A}{\sin...
35.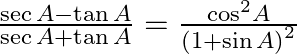
Solving L.H.S $LHS=\frac{\sec A-\tan A}{\sec A+\tan A}$ Dividing the denominator and numerator with $(\sec A+\tan A)$ and using ${{\sec }^{2}}\theta -{{\tan }^{2}}\theta =1,$we have, $=\frac{{{\sec...
34. 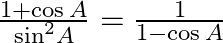
Solving L.H.S and using the trigonometric identity ${{\sin }^{2}}A+{{\cos }^{2}}A=1,$, we have ${{\sin }^{2}}A=1-{{\cos }^{2}}A$ $\Rightarrow {{\sin }^{2}}A=(1-\cos A)(1+\cos A)$ $LHS=\frac{1+\cos...
Find the adjoint of each of the following matrices:
(i) ![Rendered by QuickLaTeX.com \left[\begin{array}{cc}-3 & 5 \\ 2 & 4\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-375ad869b7946931aef27c709053c15e_l3.png)
(ii) ![Rendered by QuickLaTeX.com \left[\begin{array}{ll}a & b \\ c & d\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-79b4e1c9febd7f8cbe00652c013c9ec9_l3.png) Verify that
Verify that 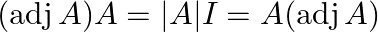 for the above matrices.
for the above matrices.
Solution: (i) Suppose $A=\left[\begin{array}{cc}-3 & 5 \\ 2 & 4\end{array}\right]$ Cofactors of $A$ are $C_{11}=4$ $C_{12}=-2$ $C_{21}=-5$ $C_{22}=-3$ Since, adj...
33.
First solve L.H.S and using the trigonometric identity we all know that ${{\sec }^{2}}\theta {{\tan }^{2}}\theta =1\Rightarrow 1+{{\tan }^{2}}\theta ={{\sec }^{2}}\theta $ $LHS=\frac{{{\sec...
32. 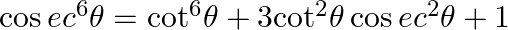
Using the trigonometric identity we get $\cos e{{c}^{2}}\theta +{{\cot }^{2}}\theta =1$ cubing it on both side ${{(\cos e{{c}^{6}}\theta +{{\cot }^{2}}\theta )}^{3}}=1$ $\cos e{{c}^{6}}-{{\cot...
31. 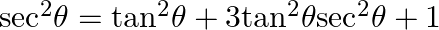
Using trigonometric identity, ${{\sec }^{2}}\theta -{{\tan }^{2}}\theta =1$ Cubing it on both side ${{({{\sec }^{2}}\theta -{{\tan }^{2}}\theta )}^{2}}=1$ ${{\sec }^{6}}\theta -{{\tan }^{6}}\theta...
30. 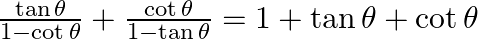
Solving L.H.S, we get $LHS=\frac{\tan \theta }{1-\frac{1}{\tan \theta }}+\frac{\cot \theta }{1-\tan \theta }$ $=\frac{{{\tan }^{2}}\theta }{\tan \theta -1}+\frac{\cot \theta }{1-\tan \theta }$...
29. 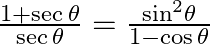
Solving L.H.S and using the trigonometric identity ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1,$we get Multiplying by $(1-\cos \theta )$to Numerator and denominator $LHS=\frac{1+\sec \theta }{\sec...
28.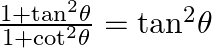
Solve L.H.S $\frac{1+{{\tan }^{2}}\theta }{1+{{\cot }^{2}}\theta }$ Using trigonometric identity${{\sec }^{2}}\theta -{{\tan }^{2}}\theta =1,and\cos e{{c}^{2}}\theta -{{\cot }^{2}}\theta =1$...
27.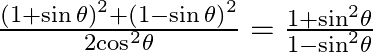
Firstly we will solve L.H.S=R.H.S Then use trigonometric identity $\sin \theta +\cos \theta =1,$, we get $LHS=\frac{{{(1+\sin \theta )}^{2}}+{{(1-\sin \theta )}^{2}}}{2{{\sec }^{2}}\theta }$...
26. 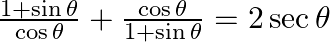
Firstly we will solve L.H.S Using the trigonometric identity ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1,$, we get $LHS=\frac{1+\sin \theta }{\cos \theta }+\frac{\cos \theta }{1+\sin \theta }$...
25. 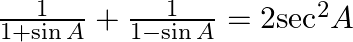
Firstly we will solve L.H.S $LHS=\frac{1}{1+\sin A}+\frac{1}{1-\sin A}$ $=\frac{(1-\sin A)+(1+\sin A)}{(1+\sin A)(1-\sin A)}$ $=\frac{1-\sin A+1+\sin A}{1-{{\sin }^{2}}A}$ $\because (1+\sin...
Find the principal value of the following:
(i) 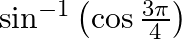
(ii) 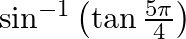
Solution: (i) Suppose $\sin ^{-1}\left(\cos \frac{3 \pi}{4}\right)=\mathrm{y}$ Therefore we can write the above equation as $\sin \mathrm{y}=\cos \frac{3 \pi}{4}=-\sin \left(\pi-\frac{3...
Find the principal value of the following:
(i) 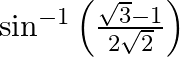
(ii) 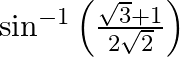
Solution: (i) It is given that functions can be written as $\sin ^{-1}\left(\frac{\sqrt{3}-1}{2 \sqrt{2}}\right)=\sin ^{-1}\left(\frac{\sqrt{3}}{2 \sqrt{2}}-\frac{1}{2 \sqrt{2}}\right) $Taking $1 /...