Answer: Direction ratios of the x-axis are 1,0,0 and direction ratios of normal to the plane are 2,−3,−6. The angle between the line and the plane,...
If the plane 2x – 3y – 6z = 13 makes an angle
Find the vector equation of a line passing through the origin and perpendicular to the plane 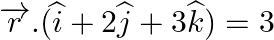
Answer:
Find the angle between the line 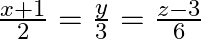 and the plane 10x + 2y – 11z = 3.
and the plane 10x + 2y – 11z = 3.
Answer: Direction ratios of the given line are 2,3,6 Direction ratios of the normal to the given plane are 10,2,−11 The angle between the line and the plane: \begin{array}{l} \sin...
Find the angle between the line 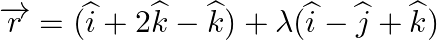 and the plane
and the plane 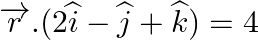
Answer: The equation of line is: $\vec{r}=(i+2 \hat{j}-\hat{k})+\lambda(\hat{i}-\hat{j}+\hat{k})$ Here, $\vec{b}=\hat{i}-j+\vec{k}$ The equation of plane is: r→·(2i^-j^+k^)=4 \vec{r}...
Find the angle between the line 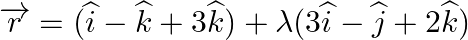 and the plane
and the plane 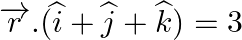
Answer: The equation of plane is: r→=(2i^-j^+3k^)+λ(3i^-j^+2k^) \vec{r}=(2 \hat{i}-\hat{j}+3 \hat{k})+\lambda(3 \hat{i}-\hat{j}+2 \hat{k}) On comparing with $\vec{r}=\vec{a}+\lambda...
Find the value of m for which the line 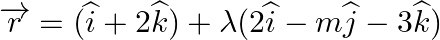 is parallel to the plane
is parallel to the plane 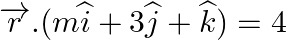
Answer: Given equation of line, $\overrightarrow r = (\widehat i + 2\widehat k) + \lambda (2\widehat i - m\widehat j - 3\widehat k)$ Comparing with the line $\overrightarrow r = \overrightarrow...
Find the angle between the line joining the points A(3,−4,−2) and B(12,2,0) and the plane 3x−y+z=1.
Answer:
Show that the line line 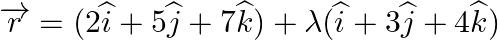 is parallel to the plane
is parallel to the plane 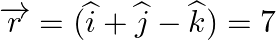 . Also, find the distance between them.
. Also, find the distance between them.
Answer: A line $\begin{array}{l} \overrightarrow r = \overrightarrow a + \lambda \overrightarrow b \\ \end{array}$ is parallel to the plane $\begin{array}{l} \overrightarrow r .\overrightarrow n ...
Find the angle between the line 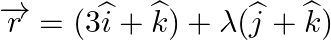 and the plane
and the plane 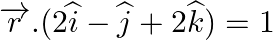
Answer: The equation of line is: r→=(3i^+k^)+λ(j^+k^) \vec{r}=(3 \hat{i}+\hat{k})+\lambda(\hat {j}+\hat{k}) Comparing with $\vec{r}=\vec{a}+\lambda \vec{b}$ $\vec{b}=(j+\dot{k})$. The...
Find the angle between the line ![Rendered by QuickLaTeX.com \[\frac{{x - 2}}{3} = \frac{{y + 1}}{{ - 1}} = \frac{{z - 3}}{{ - 2}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-24eba3255120c3288d2d203f342ddf45_l3.png)
and the plane 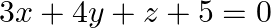
![Rendered by QuickLaTeX.com \[\frac{{x - 2}}{3} = \frac{{y + 1}}{{ - 1}} = \frac{{z - 3}}{{ - 2}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-24eba3255120c3288d2d203f342ddf45_l3.png)
Answer: The given line is $\frac{x-2}{3}=\frac{y+1}{-1}=\frac{2-3}{2}$ ⇒r→=(2i→-j→+k→)+t(3i→-j→-2k→) \Rightarrow...
Find the vector and Cartesian equations of the plane passing through the origin and parallel to the vectors 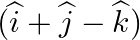 and
and 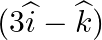 .
.
Answer:
Find the vector and Cartesian equations of the plane passing through the point (3, -1, 2) and parallel to the lines 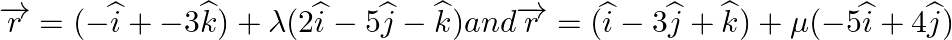 .
.
Answer:
Find the vector equation of a plane passing through the point (1, 2, 3) and parallel to the lines whose direction ratios are 1, -1, -2 and -1, 0, 2.
Answer:
Prove that the lines 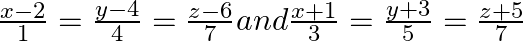 are coplanar. Also find the equation of the plane containing these lines.
are coplanar. Also find the equation of the plane containing these lines.
Answer: - 7x + 14 + 14y – 56 – 7z + 42 = 0 - 7x + 14y – 7z = 0 Multiply by negative sign, x – 2y + z = 0 The equation of...
Prove that the lines 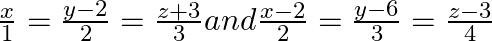 are coplanar. Also find the equation of the plane containing these lines.
are coplanar. Also find the equation of the plane containing these lines.
Answer:
Find the vector and Cartesian equations of a plane containing the two lines 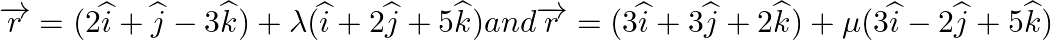 . Also show that the lines
. Also show that the lines 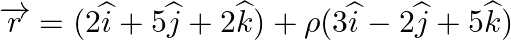 lies in the plane.
lies in the plane.
Answer: ...
Find the vector and Cartesian forms of the equations of the plane containing the two lines 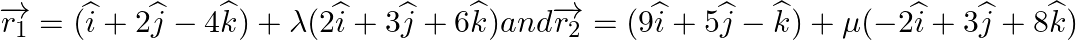 .
.
Answer:
Show that the lines 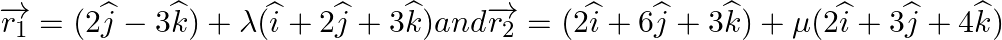 are coplanar. Also find the equation of the plane containing these lines.
are coplanar. Also find the equation of the plane containing these lines.
Answer:
Find the vector equation of a plane passing through the point (1, 2, 3) and parallel to the lines whose direction ratios are 1, -1, -2 and -1, 0, 2.
Answer:
Find the vector and Cartesian equations of the plane passing through the point (3, -1, 2) and parallel to the lines 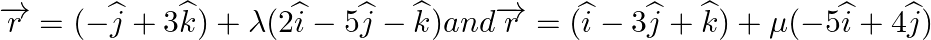
Answer:
Find the vector and Cartesian equations of the plane passing through the origin and parallel to the vectors 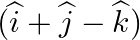 and
and 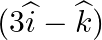 .
.
Answer:
Find the acute angle between the following planes: (i) 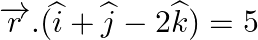 and
and 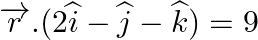 (ii)
(ii) 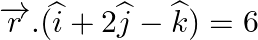 and
and 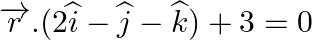 .
.
Answer: (i) (ii) ...
Find the acute angle between the following planes: (i) 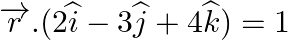 and
and 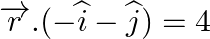 (ii)
(ii) 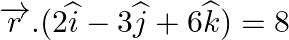 and
and 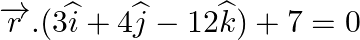 .
.
Answer: (i) (ii)
Find the value of λ for which the given planes are perpendicular to each other: (i) 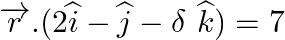 and
and 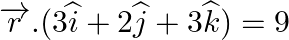 (ii)
(ii) 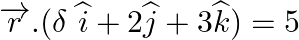 and
and 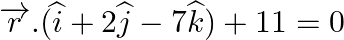 .
.
Answer: (i) For plane perpendicular, cos 900 = 0 (ii) For plane perpendicular, cos 900 = 0 (λ × 1) + (2 ×...
Show that the following planes are at right angles: (i) 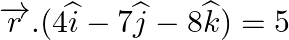 and
and 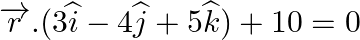 (ii)
(ii) 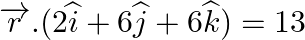 and
and 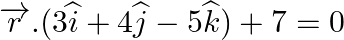 .
.
Answer: (i) (ii) = 6 + 24 – 30 = 30 – 30 = 0 = RHS Hence, the planes are...
Find the acute angle between the following planes: (i) 2x – y + z = 5 and x + y + 2z = 7 (ii) x + 2y + 2z = 3 and 2x – 3y + 6z = 8
Answer: (i) The standard equation of plane, (ii) The standard equation of plane, ...
Find the acute angle between the following planes: (i) x + y – z = 4 and x + 2y + z = 9 (ii) x + y – 2z = 6 and 2x – 2y + z = 11
Answer: (i) The standard equation of plane, (ii) The standard equation of plane, ...
Show that each of the following pairs of planes are at right angles: (i) 3x + 4y – 5z = 7 and 2x + 6y + 6z + 7 = 0 (ii) x – 2y + 4z = 10 and 18x + 17y + 4z = 49
Answer: (i) if θ = 900 then cos 900 = 0 A1A2 + B1B2 + C1C2 = 0 By comparing with the standard equation of a plane, A1 = 3, B1 = 4, C1 = -5 A2 = 2, B2 = 6, C2 = 6 LHS = A1A2 + B1B2 + C1C2 = (3 × 2) +...
Find the equation of the plane passing through the intersection of the planes x – 2y + z = 1 and 2x + y + z = 8, and parallel to the line with direction ratios 1, 2, 1. Also, find the perpendicular distance of (1, 1, 1) from the plane.
Answer: Cartesian form of equation of plane through the line of intersection of planes: ...
Find the equation of the plane passing through the line of intersection of the planes 2x – y = 0 and 3z – y = 0, and perpendicular to the plane 4x + 5y – 3z = 0.
Answer: Cartesian form of equation of plane through the line of intersection of planes: The equation...
Find the equation of the plane through the line of intersection of the planes x – 3y + z + 6 = 0 and x + 2y + 3z + 5 = 0, and passing through the origin.
Answer: Cartesian form of equation of plane through the line of intersection of planes: - x – 27y – 13z = 0 Multiplying by negative sign, x + 27y + 13z = 0 The equation of the plane is x + 27y + 13z...
Find the equation of the planes passing through the intersection of the planes 2x + 3y – z + 1 = 0 and x + y – 2z + 3 = 0, and perpendicular to the plane 3x – y – 2z – 4 = 0.
Answer: Cartesian form of equation of plane through the line of intersection of planes: The equation of the plane is 7x + 13y + 4z = 9.
Find the equation of the plane through the line of intersection of the planes x + y + z = 6 and 2x + 3y + 4z + 5 = 0, and passing through the point (1, 1, 1).
Answer: Cartesian form of equation of plane through the line of intersection of planes: 14x + 14y + 14z – 84 + 6x + 9y + 12z + 15 = 0 20x + 23y + 26z...
5. Find the equation of the plane passing through the point (1, 4, -2) and parallel to the plane 2x – y + 3z + 7 = 0.
Answer: Any plane parallel to 2x – y + 3z + 7 = 0 is shown as 2x – y + 3z + d = 0. It passes through the point (1, 4, -2) $\begin{array}{l} 2 \times 1 - 4 + 3( - 2) + d = 0\\ 2 - 4 - 6 + d = 0\\ d =...
Find the vector equation of the plane passing through the point (1, 1, 1) and parallel to the plane 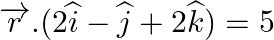 .
.
Answer:
Find the vector equation of the plane passing through the point (a, b, c) and parallel to the plane 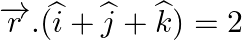 .
.
Answer:
Find the vector equation of the plane through the points 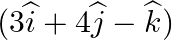 and parallel to the plane
and parallel to the plane 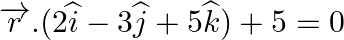 .
.
Answer:
Show that the planes 2x – y + 6z = 5 and 5x – 2.5y + 15z = 12 are parallel.
Answer:
Find the vector and Cartesian equations of a plane which is at a distance of 7 units from the origin and whose normal vector from the origin is 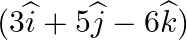
Answer: Given, $\begin{array}{l} d = 7\\ \overline n = 3\widehat i + 5\widehat j - 6\widehat k \end{array}$ The unit vector normal to the plane: ...
Find the distance of the point (2, 1, 0) from the plane 2x + y – 2z + 5 = 0.
Answer: Given plane, 2x + y – 2z + 5 = 0 The point is (2, 1, 0).
Find the distance of the point (1, 1, 2) from the plane plane 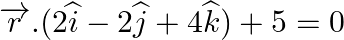 .
.
Answer: Given plane, $\overrightarrow r .(2\widehat i - 2\widehat j + 4\widehat k) + 5 = 0$ The cartesian form: 2x – 2y + 4z + 5 = 0 The point is (1, 1, 2).
Find the distance of the point (3, 4, 5) from the plane 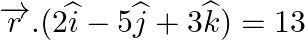 .
.
Answer: Given plane, $\overrightarrow r .(2\widehat i - 5\widehat j + 3\widehat k) = 13$ The cartesian form: 2x – 5y + 3z – 13 = 0 The point is (3, 4, 5).
Find the distance of the point 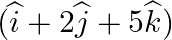 from the plane
from the plane 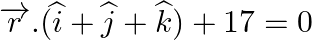 .
.
Answer: Given plane, $\overrightarrow r .(\widehat i + \widehat j + \widehat k) + 17 = 0$ The cartesian form: x + y + z +17 = 0 The point is $(\widehat i + 2\widehat j + 5\widehat k)$ => (1, 2,...
Find the distance of the point 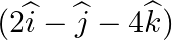 from the plane
from the plane 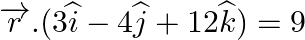 .
.
Answer: Given plane, $\overrightarrow r .(3\widehat i - 4\widehat j + 12\widehat k) = 9$ The cartesian form: 3x – 4y + 12z – 9 =0 The point is $(2\widehat i - \widehat j - 4\widehat k)$ => (2,...
Find the vector and Cartesian equations of a plane which passes through the point (1, 4, 6) and normal vector to the plane is is 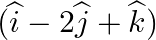
Answer: Given, A = (1, 4, 6)
Find the vector and Cartesian equations of a plane which is at a distance of 6 units from the origin and which has a normal with direction ratios 2, -1, -2.
Answer: Given, d = 6
Find the vector and Cartesian equations of a plane which is at a distance of 6/√29 from the origin and whose normal vector from the origin is is 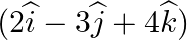
Answer: Given, = (x × 2) + (y × (-3)) + (z × 4) = 2x - 3y + 4z The Cartesian equation...
Find the vector equation of a plane which is at a distance of 5 units from the origin and which has as the unit vector normal to it.
Answer: Given, $\begin{array}{l} d = 5\\ \widehat n = \widehat k \end{array}$ The equation of plane at 5 units distance from the origin $\begin{array}{l} \widehat n \end{array}$ and as a unit...
Reduce the equation of the plane 4x – 3y + 2z = 12 to the intercept form, and hence find the intercepts made by the plane with the coordinate axes.
Answer: Equation of the plane: 4x – 3y + 2z = 12 $\begin{array}{l} \frac{4}{{12}}x - \frac{3}{{12}}y + \frac{2}{{12}}z = 1\\ \frac{x}{3} + \frac{y}{{ - 4}} + \frac{z}{6} = 1 \end{array}$ It is the...
Write the equation of the plane whose intercepts on the coordinate axes are 2, – 4 and 5 respectively.
Answer: Given, Coordinate axes are 2, - 4, 5 The equation of the variable plane: The required equation of the plane is 10x – 5y + 4z = 20.
Find the equation of the plane passing through each group of points: A (-2, 6, -6), B (-3, 10, -9) and C (-5, 0, -6)
Answer: Given, A (-2, 6, -6) B (-3, 10, -9) C (-5, 0, -6) ...
3. Show that the four points A (0, -1, 0), B (2, 1, -1), C (1, 1, 1) and D (3, 3, 0) are coplanar. Find the equation of the plane containing them.
Answer: Given, A (0, -1, 0) B (2, 1, -1) C (1, 1, 1) D (3, 3, 0) 4x – 3 (y + 1) + 2z = 0 4x – 3y + 2z – 3 = 0 Take x = 0, y = 3 and z =...
Show that the four points A (3, 2, -5), B (-1, 4, -3), C (-3, 8, -5) and D (-3, 2, 1) are coplanar. Find the equation of the plane containing them.
Answer: Let us take, The equation of the plane passing through A (3, 2, -5) a (x – 3) + b (y – 2) + c (z + 5) = 0 It passes through the points B (-1, \4, -3) and C (-3, 8, -5) a (1 – 3) + b (4 – 2)...
Find the equation of the plane passing through each group of points: (i) A (2, 2, -1), B (3, 4, 2) and C (7, 0, 6) (ii) A (0, -1, -1), B (4, 5, 1) and C (3, 9, 4)
Answer: (i) Given, A (2, 2, -1) B (3, 4, 2) C (7, 0, 6) ...
