Answer: Direction ratios of the x-axis are 1,0,0 and direction ratios of normal to the plane are 2,−3,−6. The angle between the line and the plane,...
If the plane 2x – 3y – 6z = 13 makes an angle
Find the vector equation of a line passing through the origin and perpendicular to the plane 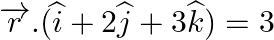
Answer:
Find the angle between the line 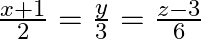 and the plane 10x + 2y – 11z = 3.
and the plane 10x + 2y – 11z = 3.
Answer: Direction ratios of the given line are 2,3,6 Direction ratios of the normal to the given plane are 10,2,−11 The angle between the line and the plane: \begin{array}{l} \sin...
Find the angle between the line 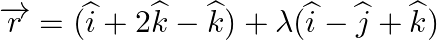 and the plane
and the plane 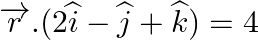
Answer: The equation of line is: $\vec{r}=(i+2 \hat{j}-\hat{k})+\lambda(\hat{i}-\hat{j}+\hat{k})$ Here, $\vec{b}=\hat{i}-j+\vec{k}$ The equation of plane is: r→·(2i^-j^+k^)=4 \vec{r}...
Find the angle between the line 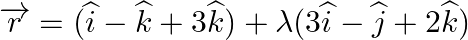 and the plane
and the plane 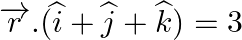
Answer: The equation of plane is: r→=(2i^-j^+3k^)+λ(3i^-j^+2k^) \vec{r}=(2 \hat{i}-\hat{j}+3 \hat{k})+\lambda(3 \hat{i}-\hat{j}+2 \hat{k}) On comparing with $\vec{r}=\vec{a}+\lambda...
Find the value of m for which the line 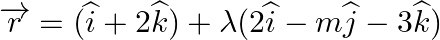 is parallel to the plane
is parallel to the plane 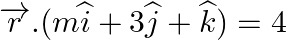
Answer: Given equation of line, $\overrightarrow r = (\widehat i + 2\widehat k) + \lambda (2\widehat i - m\widehat j - 3\widehat k)$ Comparing with the line $\overrightarrow r = \overrightarrow...
Find the angle between the line joining the points A(3,−4,−2) and B(12,2,0) and the plane 3x−y+z=1.
Answer:
Show that the line line 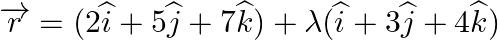 is parallel to the plane
is parallel to the plane 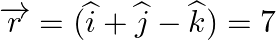 . Also, find the distance between them.
. Also, find the distance between them.
Answer: A line $\begin{array}{l} \overrightarrow r = \overrightarrow a + \lambda \overrightarrow b \\ \end{array}$ is parallel to the plane $\begin{array}{l} \overrightarrow r .\overrightarrow n ...
Find the angle between the line 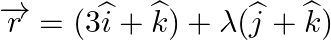 and the plane
and the plane 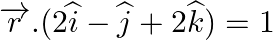
Answer: The equation of line is: r→=(3i^+k^)+λ(j^+k^) \vec{r}=(3 \hat{i}+\hat{k})+\lambda(\hat {j}+\hat{k}) Comparing with $\vec{r}=\vec{a}+\lambda \vec{b}$ $\vec{b}=(j+\dot{k})$. The...
Find the angle between the line ![Rendered by QuickLaTeX.com \[\frac{{x - 2}}{3} = \frac{{y + 1}}{{ - 1}} = \frac{{z - 3}}{{ - 2}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-24eba3255120c3288d2d203f342ddf45_l3.png)
and the plane 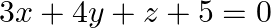
![Rendered by QuickLaTeX.com \[\frac{{x - 2}}{3} = \frac{{y + 1}}{{ - 1}} = \frac{{z - 3}}{{ - 2}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-24eba3255120c3288d2d203f342ddf45_l3.png)
Answer: The given line is $\frac{x-2}{3}=\frac{y+1}{-1}=\frac{2-3}{2}$ ⇒r→=(2i→-j→+k→)+t(3i→-j→-2k→) \Rightarrow...
Find the equation of the plane passing through each group of points: (i) A (2, 2, -1), B (3, 4, 2) and C (7, 0, 6) (ii) A (0, -1, -1), B (4, 5, 1) and C (3, 9, 4)
Answer: (i) Given, A (2, 2, -1) B (3, 4, 2) C (7, 0, 6) ...
