Solution: The standard form of a pair of Cartesian lines is:...
Find the values of p so that the lines 
and 
are at right angles.
read more
Three Dimensional Geometry
Find the values of p so that the lines
Find the equation of the plane through the intersection of the planes r.(i+3j)-6=0 and r.(3i-j-4k)=0, whose perpendicular distance from origin is unity.
According to ques,
The plane ax + by = 0 is rotated about its line of intersection with the plane z = 0 through an angle α. Prove that the equation of the plane in its new position is Ax+by
(
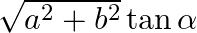)z=0
According to ques, planes are: \[~ax\text{ }+\text{ }by\text{ }=\text{ }0\text{ }\ldots .\text{ }\left( i \right)\] and \[z\text{ }=\text{ }0\text{ }\ldots .\text{ }\left( ii \right)\] hence, the...
Find the equation of the plane which is perpendicular to the plane 5x + 3y + 6z + 8 = 0 and which contains the line of intersection of the planes x + 2y + 3z – 4 = 0 and 2x + y – z + 5 = 0.
According to ques, planes are \[{{P}_{1}}:\text{ }5x\text{ }+\text{ }3y\text{ }+\text{ }6z\text{ }+\text{ }8\text{ }=\text{ }0\] \[{{P}_{2}}:\text{ }x\text{ }+\text{ }2y\text{ }+\text{ }3z\text{...
Find the shortest distance between the lines given by r=(8+3 ) i-(9+16 )j+(10=7 )k and r=15i+29j+5k+ (3i+8j-5k)
According to the ques,
Find the equations of the line passing through the point (3,0,1) and parallel to the planes x + 2y = 0 and 3y – z = 0.
According to ques, Point is \[\left( 3,\text{ }0,\text{ }1 \right)\] and the equation of planes are: \[x\text{ }+\text{ }2y\text{ }=\text{ }0\text{ }\ldots .\text{ }\left( i \right)\] and \[3y\text{...
Find the length and the foot of perpendicular from the point (1, 3/2, 2) to the plane 2x – 2y + 4z + 5 = 0.
According to ques, plane is: \[2x\text{ }\text{ }2y\text{ }+\text{ }4z\text{ }+\text{ }5\text{ }=\text{ }0\] and point: \[\left( 1,\text{ }3/2,\text{ }2 \right)\] The direction ratios of the...
Find the distance of a point (2, 4, –1) from the line (x+5)/1=(y+3)/4=(z-6)/-9
According to ques,
Find the foot of perpendicular from the point (2, 3, –8) to the line (4-x)/2=y/6=(1-z)/3 Also, find the perpendicular distance from the given point to the line.
according to ques, The coordinates of any point Q on the line are: \[x\text{ }=\text{ }-2\lambda \text{ }+\text{ }4,\text{ }y\text{ }=\text{ }6\lambda \text{ }and\text{ }z\text{ }=\text{ }-3\lambda...
Two systems of rectangular axis have the same origin. If a plane cuts them at distances a, b, c and a¢, b¢, c¢, respectively, from the origin, prove that I/a^2+1/b^2+1/c^2=1/a’^2+1/b’^2+1/c’^2
Let, \[~OX,\text{ }OY,\text{ }OZ\text{ }and\text{ }ox,\text{ }oy,\text{ }oz\] to be two rectangular systems According to ques,
O is the origin and A is (a, b, c). Find the direction cosines of the line OA and the equation of plane through A at right angle to OA.
According to ques, \[~O\text{ }\left( 0,\text{ }0,\text{ }0 \right)\text{ }and\text{ }A\left( a,\text{ }b,\text{ }c \right)\] Hence, the direction ratios of OA : \[a\text{ }\text{ }0,\text{ }b\text{...
If a variable line in two adjacent positions has direction cosines l, m, n and l + dl, m + dm, n + dn, show that the small angle dq between the two positions is given by dq2 = dl2 + dm2 + dn2
According to ques, \[~l,\text{ }m,\text{ }n\text{ }and~l~+\text{ }dl,~m~+\text{ }dm,~n~+\text{ }dn\] are the direction cosines of a variable line in two positions hence, \[{{l}^{2}}~+\text{...
Find the angle between the lines whose direction cosines are given by the equations l + m + n = 0, l2 + m2 – n2 = 0.
According to ques, Equations are, \[l~+~m~+~n~=\text{ }0\text{ }\ldots ..\text{ }\left( i \right)\] \[{{l}^{2}}~+~{{m}^{2}}~~{{n}^{2}}~=\text{ }0\text{ }\ldots .\text{ }\left( ii \right)\] From...
Find the equations of the two lines through the origin which intersect the line (x-3)/2=(y-3)/1=z/1 at angles of π/3 each.
According to ques, Any point in the given line is: \[x\text{ }\text{ }3/\text{ }2\text{ }=\text{ }y\text{ }\text{ }3/1\text{ }=\text{ }z/1\text{ }=\text{ }\lambda \] Or, \[x\text{ }=\text{ }2\lambda...
Find the equation of the plane through the points (2, 1, 0), (3, –2, –2) and (3, 1, 7).
According to ques, points are: \[\left( 2,\text{ }1,\text{ }0 \right),\text{ }\left( 3,\text{ }2,\text{ }2 \right)\text{ }and\text{ }\left( 3,\text{ }1,\text{ }7 \right)\] Since, equation of the...
If the line drawn from the point (–2, – 1, – 3) meets a plane at right angle at the point (1, – 3, 3), find the equation of the plane.
According to ques, Points are : \[\left( 2,\text{ }\text{ }1,\text{ }\text{ }3 \right)\text{ }and\text{ }\left( 1,\text{ }\text{ }3,\text{ }3 \right)\] And, Direction ratios of the normal to the...
Find the equation of a plane which is at a distance 3√3 units from origin and the normal to which is equally inclined to coordinate axis.
Since, the normal to the plane is equally inclined to the axes. so, \[cos\text{ }\alpha \text{ }=\text{ }cos\text{ }\beta \text{ }=\text{ }cos\text{ }\gamma \] or, \[So,\text{ }co{{s}^{2}}~\alpha...
Find the equation of a plane which bisects perpendicularly the line joining the points A (2, 3, 4) and B (4, 5, 8) at right angles.
According to ques, Coordinates are \[A\text{ }\left( 2,\text{ }3,\text{ }4 \right)\text{ }and\text{ }B\text{ }\left( 4,\text{ }5,\text{ }8 \right)\] Again, Coordinates of the mid-point C are...
Prove that the lines x = py + q, z = ry + s and x = p¢y + q¢, z = r¢y + s¢ are perpendicular if pp¢ + rr¢ + 1 = 0
According to ques,
Prove that the line through A (0, –1, –1) and B (4, 5, 1) intersects the line through C (3, 9, 4) and D (– 4, 4, 4).
According to ques, Points are \[~A\text{ }\left( 0,\text{ }1,\text{ }1 \right)\text{ }and\text{ }B\text{ }\left( 4,\text{ }5,\text{ }1 \right)\] \[C\text{ }\left( 3,\text{ }9,\text{ }4 \right)\text{...
Find the angle between the lines r=3i-2j+6k+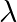
(2i+j+2k) and r=(2j-5k)+
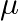(6i+3j+2k)
According to ques,
Show that the lines (x-1)/2=(y-2)/3=(z-3)/4 and (x-4)/5=(y-1)/2=z intersect. Also, find their point of intersection.
According to ques,
Find the vector equation of the line which is parallel to the vector 3i-2j+6k and which passes through the point (1, –2, 3).
According to equation of line we have,
Find the position vector of a point A in space such that vector OA is inclined at 60º to OX and at 45° to OY and vector OA = 10 units.
Since, \[co{{s}^{2}}~\alpha \text{ }+\text{ }co{{s}^{2}}~\beta \text{ }+\text{ }co{{s}^{2}}~\gamma \text{ }=\text{ }1\] or, \[co{{s}^{2}}~{{60}^{o}}~+\text{ }co{{s}^{2}}~{{45}^{o}}~+\text{...