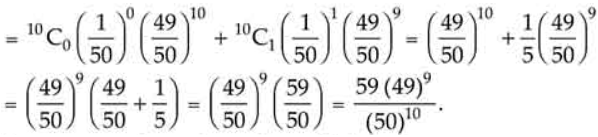![\[1/50\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-ef97cec9629bf8a7126fa4b44586a2f6_l3.png "Rendered by QuickLaTeX.com")
![\[10\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7e13914576c8f07fa7780b4b1aae684d_l3.png "Rendered by QuickLaTeX.com")
Let’s assume X to be the random variable denoting a bulb to be defective.
Here,
![\[n\text{ }=\text{ }10,\text{ }p\text{ }=\text{ }1/50,\text{ }q\text{ }=\text{ }1\text{ }\text{ }1/50\text{ }=\text{ }49/50\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-9fd37b1ee34763612a1f82f1d032c6f7_l3.png "Rendered by QuickLaTeX.com")
We know that,
![\[P\left( X\text{ }=\text{ }r \right)\text{ }={{~}^{n}}{{C}_{r}}~{{p}^{r~}}{{q}^{n\text{ }\text{ }r}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d927349adccd28b9de03d502a22a11cd_l3.png "Rendered by QuickLaTeX.com")
(i) None of the bulbs is defective, i.e.,
![\[r=0\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-371b45e1d5ae1bd003381f9898ee123b_l3.png "Rendered by QuickLaTeX.com")
![\[P\left( x\text{ }=\text{ }0 \right)\text{ }={{~}^{10}}{{C}_{0}}~{{\left( 1/50 \right)}^{0}}{{\left( 49/50 \right)}^{10\text{ }\text{ }0}}~=\text{ }{{\left( 49/50 \right)}^{10}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-bbf0e73fc3ea23315eab663a1657b0db_l3.png "Rendered by QuickLaTeX.com")
(ii) Exactly two bulbs are defective
So,
![\[P\left( x\text{ }=\text{ }2 \right)\text{ }={{~}^{10}}{{C}_{2}}~{{\left( 1/50 \right)}^{2}}{{\left( 49/50 \right)}^{10\text{ }\text{ }2}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-0f6fd5cd4fdd135b46ef8838b146220d_l3.png "Rendered by QuickLaTeX.com")
=
![\[{{45.49}^{8}}/{{50}^{10}}~=\text{ }45\text{ }\times \text{ }{{\left( 1/50 \right)}^{10}}~\times \text{ }{{49}^{8}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2f9b90a90cb40b6016c5de19fe433103_l3.png "Rendered by QuickLaTeX.com")
(iii) More than
![\[8\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-5ba6e07885b354f6c76c81fbd23c392a_l3.png "Rendered by QuickLaTeX.com")
bulbs work properly
We can say that less than
![\[2\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-b1e8e3db630df9050b1fec3c4066d5e6_l3.png "Rendered by QuickLaTeX.com")
bulbs are defective
![\[P\left( x\text{ }<\text{ }2 \right)\text{ }=\text{ }P\left( x\text{ }=\text{ }0 \right)\text{ }+\text{ }P\left( x\text{ }=\text{ }1 \right)\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-049448dbbb6e3e6a554372372e42f55f_l3.png "Rendered by QuickLaTeX.com")
