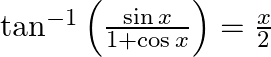Solution: To Prove: $\tan ^{-1}\left(\frac{\sin x}{1+\cos x}\right)=\frac{x}{2}$ Formula Used: 1) $\sin A=2 \times \sin \frac{A}{2} \times \cos \frac{A}{2}$ 2) $1+\cos A=2 \cos ^{2} \frac{A}{2}$...
Prove that:
Prove that: 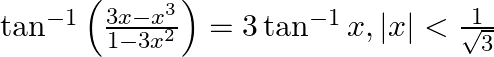
Solution: To Prove: $\tan ^{-1}\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right)=3 \tan ^{-1} x$ Formula Used: $\tan 3 A=\frac{3 \tan A-\tan ^{3} A}{1-3 \tan ^{2} A}$ Proof: $\text { LHS }=\tan...
Prove that: 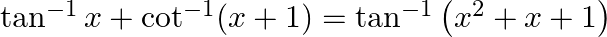
Solution: To Prove: $\tan ^{-1} x+\cot ^{-1}(x+1)=\tan ^{-1}\left(x^{2}+x+1\right)$ Formula Used: 1) $\cot ^{-1} \mathrm{x}=\tan ^{-1} \frac{1}{\mathrm{x}}$ 2) $\tan ^{-1} \mathrm{x}+\tan ^{-1}...
In ∆ABC, D and E are the midpoints of AB and AC respectively. Find the ratio of the areas of ∆ADE and ∆ABC.
Answer: Given, D and E are midpoints of AB and AC. Applying midpoint theorem, DE ‖ BC. By B.P.T., $\frac{A D}{A B}=\frac{A E}{A C}$ ∠???? = ∠???? Applying SAS similarity...
In the given figure, DE║BC and DE: BC = 3:5. Calculate the ratio of the areas of ∆ADE and the trapezium BCED.
Answer: Given, DE || BC. ∠???????????? = ∠???????????? (???????????????????????????????????????????????????? ????????????????????????) ∠???????????? = ∠????????????...
∆ABC is right angled at A and AD⊥BC. If BC = 13cm and AC = 5cm, find the ratio of the areas of ∆ABC and ∆ADC.
Answer: In ∆ABC and ∆ADC, ∠???????????? = ∠???????????? = 900 ∠???????????? = ∠???????????? (????????????????????????) By AA similarity, ∆ BAC~ ∆ ADC. The ratio of the areas of...
In the given figure, DE║BC. If DE = 3cm, BC = 6cm and ar(∆ADE) = 15cm2, find the area of ∆ABC.
Answer: Given, DE || BC ∴ ∠???????????? = ∠???????????? (???????????????????????????????????????????????????? ????????????????????????) ∠???????????? = ∠????????????...
In the given figure, ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. If AP = 1cm, PB = 3cm, AQ = 1.5cm, QC = 4.5cm, prove that area of ∆APQ is 1/16 of the area of ∆ABC.
Answer: Given, $\frac{A P}{A B}=\frac{1}{1+3}=\frac{1}{4}$ $\frac{A Q}{A C}=\frac{1.5}{1.5+4.5}=\frac{1.5}{6}=\frac{1}{4}$ $\frac{A P}{A B}=\frac{A Q}{A C}$ ∠???? = ∠???? By SAS...
The areas of two similar triangles are 64cm2 and 100cm2 respectively. If a median of the smaller triangle is 5.6cm, find the corresponding median of the other.
Answer: Let the two triangles be ABC and PQR with medians AM and PN, The ratio of areas of two similar triangles will be equal to the ratio of squares of their corresponding...
The areas of two similar triangles are 81cm2 and 49cm2 respectively. If the altitude of the first triangle is 6.3cm, find the corresponding altitude of the other.
Answer: Given, Triangles are similar The areas of these triangles will be equal to the ratio of squares of their corresponding sides. The ratio of areas of two similar triangles...
The corresponding altitudes of two similar triangles are 6cm and 9cm respectively. Find the ratio of their areas.
Answer: Let the two triangles be ABC and DEF with altitudes AP and DQ, Given, ∆ ABC ~ ∆ DEF. The ratio of areas of two similar triangles is equal to the ratio of squares of...
∆ABC ~ ∆DEF and their areas are respectively 100cm2 and 49cm2 . If the altitude of ∆ABC is 5cm, find the corresponding altitude of ∆DEF.
Answer: Given, ∆ABC ~ ∆DEF. The ration of the areas of these triangles will be equal to the ratio of squares of their corresponding sides. The ratio of areas of two similar...
The areas of two similar triangles are 169cm2 and 121cm2 respectively. If the longest side of the larger triangle is 26cm, find the longest side of the smaller triangle.
Answer: Given, Triangles are similar. The ratio of the areas of these triangles will be equal to the ratio of squares of their corresponding sides. Let the longest side of smaller triangle be X cm....
∆ABC~∆PQR and ar(∆ABC) = 4, ar(∆PQR). If BC = 12cm, find QR.
Answer: Given, ???????? ( ∆ ???????????? ) = 4???????? (∆ ???????????? ) \begin{equation} \frac{\operatorname{ar}(\triangle A B C)}{\operatorname{ar}(\Delta P Q R)}=\frac{4}{1} \end{equation} ∵ ∆ABC...
The areas of two similar triangles ABC and PQR are in the ratio 9:16. If BC = 4.5cm, find the length of QR.
Answer: Given, ∆ ABC ~ ∆ PQR The ratio of the areas of triangles will be equal to the ratio of squares of their corresponding sides. \begin{equation} \frac{\operatorname{ar}(\triangle A B...
∆ABC~∆DEF and their areas are respectively 64 cm2 and 121cm2. If EF = 15.4cm, find BC.
Answer: Given, ∆ ABC ~ ∆ DEF. The ratio of the areas of these triangles will be equal to the ration of squares of their corresponding sides. $\eqalign{ & \frac{ar(\vartriangle...