Solution: Given: $\sin ^{-1} x-\cos ^{-1} x=\frac{\pi}{6}$ We know that $\sin ^{-1} \mathrm{x}+\cos ^{-1} \mathrm{x}=\frac{\pi}{2}$ So, $\sin ^{-1} x=\frac{\pi}{2}-\cos ^{-1} x$ Substituting in the...
Solve for
Solve for  :
: 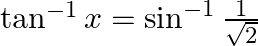
Solution: To find: value of $x$ Given: $\tan ^{-1} \mathrm{x}=\sin ^{-1} \frac{1}{\sqrt{2}}$ We know that $\sin \frac{\pi}{4}=\frac{1}{\sqrt{2}}$ Therefore, $\frac{\pi}{4}=\sin ^{-1}...
Solve for  :
: 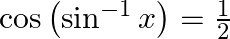
Solution: To find: value of $x$ Given: $\cos \left(\sin ^{-1} \mathrm{x}\right)=\frac{1}{2}$ $\text { LHS }=\cos \left(\sin ^{-1} x\right)$ $\begin{array}{l} =\cos \left(\cos...
Solve for  :
: 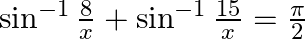
Solution: To find: value of $x$ Given: $\sin ^{-1} \frac{\mathrm{g}}{\mathrm{x}}+\sin ^{-1} \frac{15}{\mathrm{x}}=\frac{\pi}{2}$ We know $\sin ^{-1} \mathrm{x}+\cos ^{-1} \mathrm{x}=\frac{\pi}{2}$...
Solve for  :
: 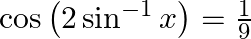
Solution: To find: value of $x$ Formula Used: $2 \sin ^{-1} x=\sin ^{-1}\left(2 x \sqrt{1-x^{2}}\right)$. Given: $\cos \left(2 \sin ^{-1} x\right)=\frac{1}{9}$ $\text { LHS }=\cos \left(2 \sin ^{-1}...
Solve for 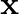 :
: 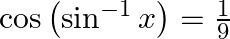
Solution: To find: value of $x$ Given: $\cos \left(\sin ^{-1} x\right)=\frac{1}{9}$ $\mathrm{LHS}=\cos \left(\sin ^{-1} \mathrm{x}\right) \ldots(1)$ Let $\sin \theta=x$ Therefore $\theta=\sin ^{-1}...
Solve for x: 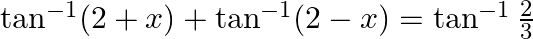
Solution: To find: value of $x$ Formula Used: $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$ where xy $<1$ Given: $\tan ^{-1}(2+x)+\tan ^{-1}(2-x)=\tan ^{-1} \frac{2}{3}$...
Solve for  :
: 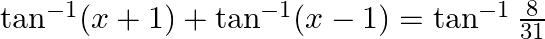
Solution: To find: value of $x$ Formula Used: $\tan ^{-1} \mathrm{x}+\tan ^{-1} \mathrm{y}=\tan ^{-1}\left(\frac{\mathrm{x}+y}{1-\mathrm{xy}}\right)$ where $\mathrm{xy}<1$ Given: $\tan...
Prove that: 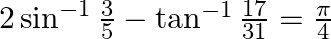
Solution: To Prove: $2 \sin ^{-1} \frac{3}{5}-\tan ^{-1} \frac{17}{31}=\frac{\pi}{4}$ Formula Used: 1) $2 \sin ^{-1} x=\sin ^{-1}\left(2 x \times \sqrt{1-x^{2}}\right)$ 2) $\tan ^{-1}...
Prove that: 
Solution: To Prove: $\sin ^{-1} \frac{1}{\sqrt{17}}+\cos ^{-1} \frac{9}{\sqrt{85}}=\tan ^{-1} \frac{1}{2}$ Formula Used: $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$ where $x...
Prove that: 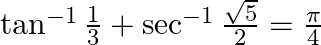
Solution: To Prove: $\tan ^{-1} \frac{1}{3}+\sec ^{-1} \frac{\sqrt{5}}{2}=\frac{\pi}{4}$ Formula Used: $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$ where $x y<1$ Proof:...
Prove that: 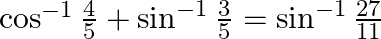
Solution: To Prove: $\cos ^{-1} \frac{4}{5}+\sin ^{-1} \frac{3}{5}=\sin ^{-1} \frac{27}{11}$ Formula Used: $\sin ^{-1} x+\sin ^{-1} y=\sin ^{-1}\left(x \times \sqrt{1-y^{2}}+y \times...
Prove that: 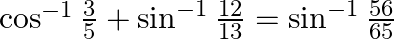
Solution: To Prove: $\cos ^{-1} \frac{3}{5}+\sin ^{-1} \frac{12}{13}=\sin ^{-1} \frac{56}{65}$ Formula Used: $\sin ^{-1} \mathrm{x}+\sin ^{-1} \mathrm{y}=\sin ^{-1}\left(\mathrm{x} \times...
Prove that: 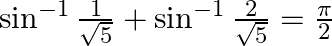
Solution: To Prove: $\sin ^{-1} \frac{1}{\sqrt{5}}+\sin ^{-1} \frac{2}{\sqrt{5}}=\frac{\pi}{2}$ Formula Used: $\sin ^{-1} \mathrm{x}+\sin ^{-1} \mathrm{y}=\sin ^{-1}\left(\mathrm{x} \times...
Prove that: 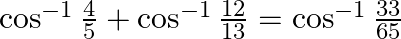
Solution: To Prove: $\cos ^{-1} \frac{4}{5}+\cos ^{-1} \frac{12}{13}=\cos ^{-1} \frac{33}{65}$ Formula Used: $\cos ^{-1} x+\cos ^{-1} y=\cos ^{-1}\left(x y-\sqrt{1-x^{2}} \times...
Prove that: 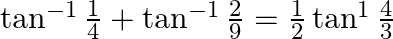
Solution: To Prove: $\tan ^{-1} \frac{1}{4}+\tan ^{-1} \frac{2}{9}=\frac{1}{2} \tan ^{-1} \frac{4}{3} \Rightarrow 2\left(\tan ^{-1} \frac{1}{4}+\tan ^{-1} \frac{2}{9}\right)=\tan ^{-1} \frac{4}{3}$...
Prove that: 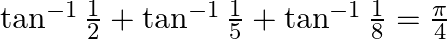
Solution: To Prove: $\tan ^{-1} \frac{1}{2}+\tan ^{-1} \frac{1}{5}+\tan ^{-1} \frac{1}{8}=\frac{\pi}{4}$ Formula Used: $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$ where $x...
Prove that: 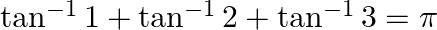
Solution: To Prove: $\tan ^{-1} 1+\tan ^{-1} 2+\tan ^{-1} 3=\pi$ Formula Used: $\tan ^{-1} \mathrm{x}+\tan ^{-1} \mathrm{y}=\pi+\tan ^{-1}\left(\frac{\mathrm{x}+\mathrm{y}}{1-\mathrm{xy}}\right)$...
Prove that: 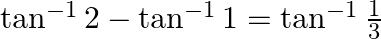
Solution: To Prove: $\tan ^{-1} 2-\tan ^{-1} 1=\tan ^{-1} \frac{1}{3}$ Formula Used: $\tan ^{-1} \mathrm{x}-\tan ^{-1} \mathrm{y}=\tan ^{-1}\left(\frac{\mathrm{x}-\mathrm{y}}{1+\mathrm{xy}}\right)$...
Prove that: 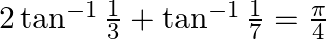
Solution: To Prove: $2 \tan ^{-1} \frac{1}{3}+\tan ^{-1} \frac{1}{7}=\frac{\pi}{4}$ Formula Used: $\tan ^{-1} \mathrm{x}+\tan ^{-1} \mathrm{y}=\tan...
Prove that: 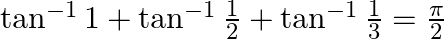
Solution: To Prove: $\tan ^{-1} 1+\tan ^{-1} \frac{1}{2}+\tan ^{-1} \frac{1}{3}=\frac{\pi}{2}$ Formula Used: $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$ Proof:...
Prove that: 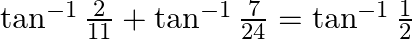
Solution: To Prove: $\tan ^{-1} \frac{2}{11}+\tan ^{-1} \frac{7}{24}=\tan ^{-1} \frac{1}{2}$ Formula Used: $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$ Proof:...
Prove that: 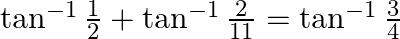
Solution: To Prove: $\tan ^{-1} \frac{1}{2}+\tan ^{-1} \frac{2}{11}=\tan ^{-1} \frac{3}{4}$ Formula Used: $\tan ^{-1} \mathrm{x}+\tan ^{-1} \mathrm{y}=\tan...
Prove that: 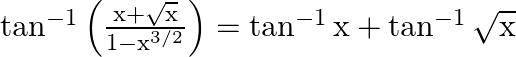
Solution: We know that, $\tan ^{-1}\left(\frac{A+B}{1-A B}\right)=\tan ^{-1} A+\tan ^{-1} B$ Now, taking $A=x$ and $B=\sqrt{x}$ We get, $\tan ^{-1} x+\tan ^{-1} \sqrt{x}=\tan...
Prove that: 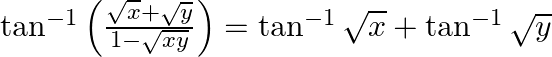
Solution: To Prove: $\tan ^{-1}\left(\frac{\sqrt{x}+\sqrt{y}}{1-\sqrt{x y}}\right)=\tan ^{-1} \sqrt{x}+\tan ^{-1} \sqrt{y}$ We know that, $\tan A+\tan B=\frac{\tan A+\tan B}{1-\tan A \tan B}$ Also,...
Prove that: 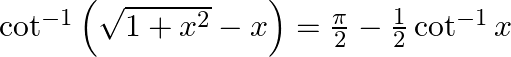
Solution: To Prove: $\cot ^{-1}\left(\sqrt{1+x^{2}}-x\right)=\frac{\pi}{2}-\frac{1}{2} \cot ^{-1} x$ Formula Used: 1) $\tan \left(\frac{\pi}{4}+A\right)=\frac{1+\tan A}{1-\tan A}$ 2)...
Prove that: 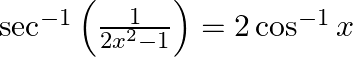
Solution: To Prove: $\sec ^{-1}\left(\frac{1}{2 x^{2}-1}\right)=2 \cos ^{-1} x$ Formula Used: 1) $\cos 2 A=2 \cos ^{2} A-1$ 2) $\cos ^{-1} A=\sec ^{-1}\left(\frac{1}{A}\right)$ Proof:...
Prove that: 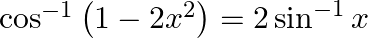
Solution: To Prove: $\cos ^{-1}\left(1-2 x^{2}\right)=2 \sin ^{-1} x$ Formula Used: $\cos 2 A=1-2 \sin ^{2} A$ Proof: $\operatorname{LHS}=\cos ^{-1}\left(1-2 x^{2}\right) \ldots(1)$ Let $x=\sin A...
Prove that: 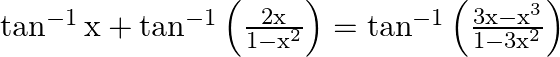
Solution: To Prove: $\tan ^{-1} x+\tan ^{-1}\left(\frac{2 x}{1-x^{2}}\right)=\tan ^{-1}\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right)$ Formula Used: $\tan ^{-1} x+\tan ^{-1} y=\tan...
Prove that: 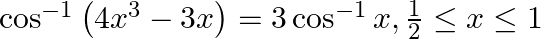
Solution: To Prove: $\cos ^{-1}\left(4 x^{3}-3 x\right)=3 \cos ^{-1} x$ Formula Used: $\cos 3 A=4 \cos ^{3} A-3 \cos A$ Proof: $\text { LHS }=\cos ^{-1}\left(4 x^{3}-3 x\right) \ldots(1)$ Let...
Prove that: 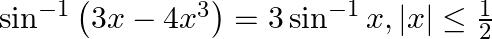
Solution: To Prove: $\sin ^{-1}\left(3 x-4 x^{3}\right)=3 \sin ^{-1} x$ Formula Used: $\sin 3 \mathrm{~A}=3 \sin \mathrm{A}-4 \sin ^{3} \mathrm{~A}$ Proof: $\operatorname{LHS}=\sin ^{-1}\left(3 x-4...
Prove that: 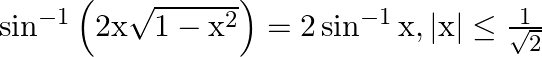
Solution: To Prove: $\sin ^{-1}\left(2 x \sqrt{1-x^{2}}\right)=2 \sin ^{-1} x$ Formula Used: $\sin 2 A=2 \times \sin A \times \cos A$ Proof: $\text { LHS }=\sin ^{-1}\left(2 x \sqrt{1-x^{2}}\right)...
Prove that: 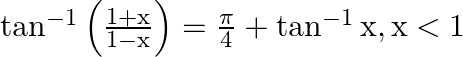
Solution: To Prove: $\tan ^{-1}\left(\frac{1+x}{1-x}\right)=\frac{\pi}{4}+\tan ^{-1} x$ Formula Used: $\tan \left(\frac{\pi}{4}+A\right)=\frac{1+\tan A}{1-\tan A}$ Proof: $\mathrm{LHS}=\tan...
