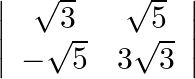Solution: $\left|\begin{array}{cc}\sqrt{3} & \sqrt{5} \\ -\sqrt{5} & 3 \sqrt{3}\end{array}\right| \cdot=3 \sqrt{3} \times \sqrt{3}-(-\sqrt{5} \times \sqrt{5})$ $=14$
Evaluate
Evaluate 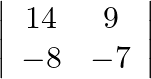
Solution: $\begin{array}{l} \left|\begin{array}{cc} 14 & 9 \\ -8 & -7 \end{array}\right|=14 \times(-7)-9 \times(-8) \\ =-26 \end{array}$
For what value of  , the given matrix
, the given matrix ![Rendered by QuickLaTeX.com A=\left[\begin{array}{cc}3-2 x & x+1 \\ 2 & 4\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-6d1f81dc4f5441083b9e76c825f8968a_l3.png) is a singular matrix?
is a singular matrix?
Solution: For $A$ to be singular matrix its determinant should be equal to 0 . $\begin{array}{l} 0=(3-2 x) \times 4-(x+1) \times 2 \\ 0=12-8 x-2 x-2 \\ 0=10-10 x \\ x=1 \end{array}$
Without expanding the determinant, prove that 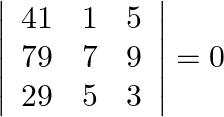 . SINGULAR MATRIX A square matrix
. SINGULAR MATRIX A square matrix 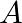 is said to be singular if
is said to be singular if 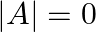 . Also,
. Also, 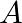 is called non singular if
is called non singular if 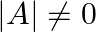 .
.
Solution: We know that $C_{1} \Rightarrow C_{1}-C_{2}$, would not change anything for the determinant. Applying the same in above determinant, we get $\left[\begin{array}{lll}40 & 1 & 5 \\...
Evaluate 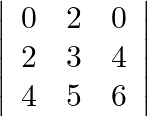
Solution: We know that expansion of determinant with respect to first row is $a_{11} A_{11}+a_{12} A_{12}+a_{13} A_{13}$. $0(3 \times 6-5 \times 4)-2(2 \times 6-4 \times 4)+0(2 \times 5-4 \times 3)$...
Evaluate 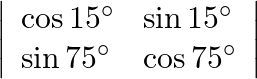
Solution: $\begin{array}{l} \cos 15^{\circ} \cos 75^{\circ}-\sin 75^{\circ} \sin 15^{\circ} \\ =\cos \left(15^{\circ}+75^{\circ}\right) \because \cos A \cos B-\sin A \sin B=\cos (A+B) \\ =\cos...
Evaluate 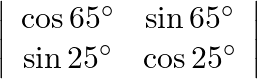
Solution: By directly opening this determinant $\begin{array}{l} \cos 65^{\circ} \times \cos 25^{\circ}-\sin 25^{\circ} \times \sin 65^{\circ} \\ =\cos \left(65^{\circ}+25^{\circ}\right) \because...
Evaluate 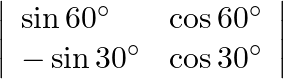
Solution: After finding determinant we will get, $\begin{array}{l} \operatorname{Sin} 60^{\circ}=\frac{\sqrt{3}}{2}=\cos 30^{\circ} \\ \operatorname{Cos} 60^{\circ}=\frac{1}{2}=\sin 30^{\circ} \\...
Evaluate 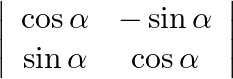
Solution: After finding determinant we will get a trigonometric identity. $\begin{array}{l} \cos ^{2} \alpha+\sin ^{2} \alpha \\ =1 \end{array}$ $\because \sin ^{2} \theta+\cos ^{2} \theta=1$
Evaluate 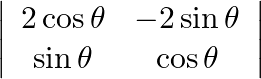
Solution: After finding determinant we will get a trigonometric identity. $\begin{array}{l} 2 \cos ^{2} \theta+2 \sin ^{2} \theta \\ =2 \\ \because \sin ^{2} \theta+\cos ^{2} \theta=1...
Evaluate 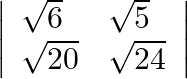 .
.
Solution: Find determinant $\begin{array}{l} \sqrt{6} \times \sqrt{24-\sqrt{2}} 20 \times \sqrt{5} \\ \sqrt{1} 144-\sqrt{1} 100 \\ =12-10 \\ =2 \end{array}$
Evaluate 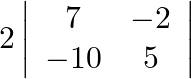 .
.
Solution: It is determinant multiplied by a scalar number 2 , just find determinant of matrix and multiply it by 2 . $\begin{array}{l} 2 \times(35-20) \\ 2 \times 15=30 \end{array}$
If ![Rendered by QuickLaTeX.com \mathrm{A}=\left[\begin{array}{ll}3 & 4 \\ 1 & 2\end{array}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-9332ef694cc023ffd6fab878ba6dae64_l3.png) , find the value of
, find the value of 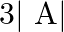 .
.
Solution: Find the determinant of $A$ and then multiply it by 3 $\begin{array}{l} |A|=2 \\ 3|A|=3 \times 2 \\ =6 \end{array}$
If 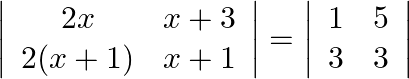 , write the value of
, write the value of  .
.
Solution: Simply by equating both sides we can get the value of $x$. $\begin{array}{l} 2 x^{2}+2 x-2\left(x^{2}+4 x+3\right)=-12 \\ \Rightarrow-6 x-6=-12 \\ \Rightarrow-6 x=-6 \\ \Rightarrow x=1...
If 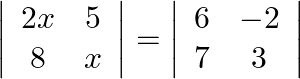 , write the value of
, write the value of  .
.
Solution: This question is having the same logic as above. $\begin{array}{l} 2 x^{2}-40=18+14 \\ \Rightarrow 2 x^{2}=72 \\ \Rightarrow x^{2}=36 \\ \Rightarrow x=\pm 6 \end{array}$
If 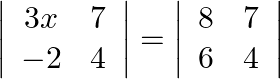 , write the value of
, write the value of  .
.
Solution: Here the determinant is compared so we need to take determinant both sides then find $\mathrm{x}$. $\begin{array}{l} 12 x+14=32-42 \\ \Rightarrow 12 x=-10-14 \\ \Rightarrow 12 x=-24 \\...
Evaluate 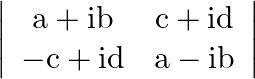
Solution: This we can very simply go through directly. $\begin{array}{l} ((a+i b)(a-i b))-((-c+i d)(c+i d)) \\ \Rightarrow\left(a^{2}+b^{2}\right)-\left(-c^{2}-d^{2}\right) \\ \Rightarrow...
Evaluate 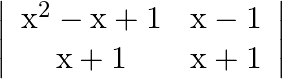
Solution: Theorem: This evaluation can be done in two different ways either by taking out the common things anc then calculating the determinants or simply take determinant. I will prefer first...
If 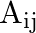 is the cofactor of the element
is the cofactor of the element 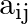 of
of 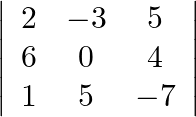 then write the value of
then write the value of 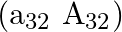 .
.
Solution: Theorem: $A_{i j}$ is found by deleting $j^{t h}$ rowand $j^{t h}$ column, the determinant of left matrix is called cofactor with multiplied by $(-1)^{(i+j)}$ Given: $\mathrm{j}=3$ and...
If 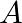 is a
is a  matrix such that
matrix such that 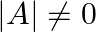 and
and 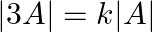 then write the value of
then write the value of 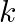 .
.
Solution: Theorem: If Let $A$ be $k \times k$ matrix then $|p A|=p^{k}|A|$. Given: $\mathrm{k}=3$ and $\mathrm{p}=3$. $\begin{array}{l} |3 \mathrm{~A}|=3^{3} \times|\mathrm{A}| \\ =27|\mathrm{~A}|...
If 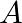 is a
is a  matrix such that
matrix such that 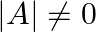 and
and 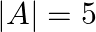 , write the value of
, write the value of 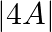 .
.
Solution: Theorem: If $A$ be $k \times k$ matrix then $|p A|=p^{k}|A|$. Given, $\mathrm{p}=4, \mathrm{k}=2$ and $|\mathrm{A}|=5$. $\begin{array}{l} |4 \mathrm{~A}|=4^{2} \times 5 \\ =16 \times 5 \\...