$\begin{array}{l} x^{2}+6 x-\left(a^{2}+2 a-8\right)=0 \\ \Rightarrow x^{2}+6 x-(a+4)(a-2)=0 \\ \Rightarrow x^{2}+[(a+4)-(a-2)] x-(a+4)(a-2)=0 \\ \Rightarrow x^{2}+(a+4) x-(a-2) x-(a+4)(a-2)=0 \\...
Solve 
read more
Quadratic Equations
Solve
Solve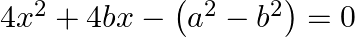 
$\begin{array}{l} 4 x^{2}+4 b x-\left(a^{2}-b^{2}\right)=0 \\ \Rightarrow 4 x^{2}+4 b x-(a-b)(a+b)=0 \\ \Rightarrow 4 x^{2}+2[(a+b)-(a-b)] x-(a-b)(a+b)=0 \\ \Rightarrow 4 x^{2}+2(a+b) x-2(a-b)...
Solve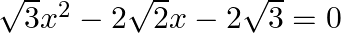 
$\begin{array}{l} \sqrt{3} x^{2}-2 \sqrt{2} x-2 \sqrt{3}=0 \\ \Rightarrow \sqrt{3} x^{2}-3 \sqrt{2} x+\sqrt{2} x-2 \sqrt{3}=0 \\ \Rightarrow \sqrt{3} x(x-\sqrt{6})+\sqrt{2}(x-\sqrt{6})=0 \\...
Solve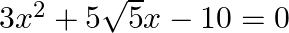 
$\begin{array}{l} 3 x^{2}+5 \sqrt{5} x-10=0 \\ \Rightarrow 3 x^{2}+6 \sqrt{5} x-\sqrt{5} x-10=0 \\ \Rightarrow 3 x(x+2 \sqrt{5})-\sqrt{5}(x+2 \sqrt{5})=0 \\ \Rightarrow(x+2 \sqrt{5})(3 x-\sqrt{5})=0...
Solve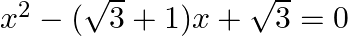 
$\begin{array}{l} x^{2}-(\sqrt{3}+1) x+\sqrt{3}=0 \\ \Rightarrow x^{2}-\sqrt{3} x-x+\sqrt{3}=0 \\ \Rightarrow x(x-\sqrt{3})-1(x-\sqrt{3})=0 \\ \Rightarrow(x-\sqrt{3})(x-1)=0 \\ \Rightarrow...
Find the value of 
for which the quadratic equation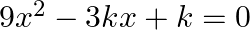 
has equal roots.
It is given that the quadratic equation $9 x^{2}-3 k x+k=0$ has equal roots. $\begin{array}{l} \therefore D=0 \\ \Rightarrow(-3 k)^{2}-4 \times 9 \times k=0 \\ \Rightarrow 9 k^{2}-36 k=0 \\...
If the roots of the quadratic equation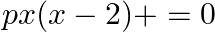 
are equal, find the value of 
.
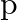It is given that the roots of the quadratic equation $p x^{2}-2 p x+6=0$ are equal. $\begin{array}{l} \therefore D=0 \\ \Rightarrow(-2 p)^{2}-4 \times p \times 6=0 \\ \Rightarrow 4 p^{2}-24 p=0 \\...
If one zero of the polynomial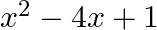 
is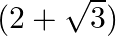 
, write the other zero.
Let the other zero of the given polynomial be $\alpha$. Now, Sum of the zeroes of the given polynomial $=\frac{-(-4)}{1}=4$ $\begin{array}{l} \therefore \alpha+(2+\sqrt{3})=4 \\ \Rightarrow...
If the quadratic equation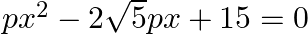 
has two equal roots then find the value of .
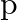It is given that the quadratic equation $p x^{2}-2 \sqrt{5} p x+15=0$ has two equal roots. $\begin{array}{l} \therefore D=0 \\ \Rightarrow(-2 \sqrt{5} p)^{2}-4 \times p \times 15=0 \\ \Rightarrow 20...
Find the solution of the quadratic equation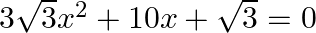 
.
The given quadratic equation is $3 \sqrt{3} x^{2}+10 x+\sqrt{3}=0$ $\begin{array}{l} 3 \sqrt{3} x^{2}+10 x+\sqrt{3}=0 \\ \Rightarrow 3 \sqrt{3} x^{2}+9 x+x+\sqrt{3}=0 \\ \Rightarrow 3 \sqrt{3}...
Find the roots of the quadratic equation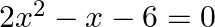 
.
The given quadratic equation is $2 x^{2}-x-6=0$ $\begin{array}{l} 2 x^{2}-x-6=0 \\ \Rightarrow 2 x^{2}-4 x+3 x-6=0 \\ \Rightarrow 2 x(x-2)+3(x-2)=0 \\ \Rightarrow(x-2)(2 x+3)=0 \\ \Rightarrow x-2=0...
Show that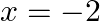 
is a solution of 
.
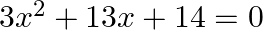The given equation is $3 x^{2}+13 x+14=0$. Putting $x=-2$ in the given equation, we get $L H S-3 \times(-2)^{2}+13 \times(-2)+14=12-26+14=0=R H S$ $\therefore x=-2$ is a solution of the given...
The roots of the quadratic equation 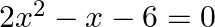. are
(a)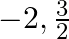 
(b)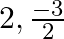 
(c) 
(d) 
Answer is (b) $2, \frac{-3}{2}$ The given quadratic equation is $2 x^{2}-x-6=0$. $\begin{array}{l} 2 x^{2}-x-6=0 \\ \Rightarrow 2 x^{2}-4 x+3 x-6=0 \\ \Rightarrow 2 x(x-2)+3(x-2)=0 \\...
If the equation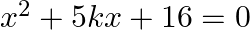 
has no real roots then
(a)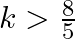 
(b)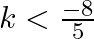 
(c)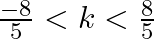 
(d) None of these
Answer is (c) $\frac{-8}{5}<k<\frac{8}{5}$ It is given that the equation $\left(x^{2}+5 k x+16=0\right)$ has no real roots. $\begin{array}{l} \therefore\left(b^{2}-4 a c\right)<0 \\...
In the equation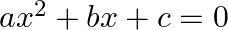 
, it is given that 
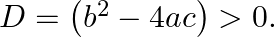Then, the roots of the equation are
(a) real and equal
(b) real and unequal
(c) imaginary
(d) none of these
Answer is (b) real and unequal We know that when discriminant, $D>0$, the roots of the given quadratic cquation are real and uncqual.
If the equation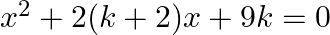 
has equal roots then 
?
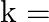(a) 1 or 4
(b)-1 or 4
(c) 1 or -4
(d) -1 or -4
Answer is (a) 1 or 4 It is given that the roots of the equation $\left(x^{2}+2(k+2) x+9 k=0\right)$ are equal. $\begin{array}{l} \therefore\left(b^{2}-4 a c\right)=0 \\ \Rightarrow\{2(k+2)\}^{2}-4...
If the roots of the equation 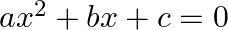are equal then 
?
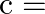(a)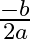 
(b)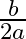 
(c)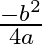 
(d)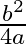 
Answer is (d) $\frac{b^{2}}{4 a}$ It is given that the roots of the equation $\left(a x^{2}+b x+c=0\right)$ are equal. $\begin{array}{l} \therefore\left(b^{2}-4 a c\right)=0 \\ \Rightarrow b^{2}=4 a...
If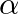 
and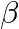 
are the roots of the equation 
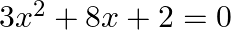then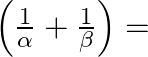 
?
(a)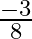 
(b)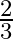 
(c)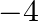 
(d) 4
Answer is (c) $-4$ It is given that $\alpha$ and $\beta$ are the roots of the equation $3 x^{2}+8 x+2=0$ $\therefore \alpha+\beta=-\frac{8}{3}$ and $\alpha \beta=\frac{2}{3}$...
If the sum of the roots of the equation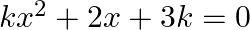 
is equal to their product then the value of
(a)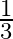 
(b)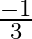 
(c)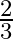
(d)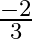 
Answer is (d) $\frac{-2}{3}$ Given: $k x^{2}+2 x+3 k=0$ Sum of the roots $=$ Product of the roots $\begin{array}{l} \Rightarrow \frac{-2}{k}=\frac{3 k}{k} \\ \Rightarrow 3 k=-2 \\ \Rightarrow...
The ratio of the sum and product of the roots of the equation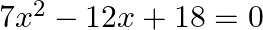 
is
(a)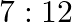 
(b)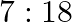 
(c)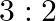 
(d)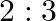 
Answer is (d) $2: 3$ Given: $7 x^{2}-12 x+18=0$ $\therefore \alpha+\beta=\frac{12}{7}$ and $\beta=\frac{18}{7}$, where $\alpha$ and $\beta$ are the roots of the equation $\therefore$ Ratio of the...
The sum of the roots of the equation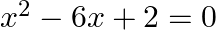 
is
(a) 2
(b)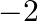 
(c) 6
(d)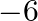 
Answer is (b) -2 Sum of the roots of the equation $x^{2}-6 x+2=0$ is $\alpha+\beta=\frac{-b}{a}=\frac{-(-6)}{1}=6$, where $\alpha$ and $\beta$ are the roots of the equation.
If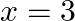 
is a solution of the equation 
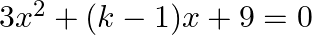, then 
?
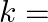(a)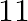 
(b)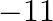 
(c)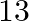 
(d)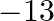 
Answer is (b) $-11$ It is given that $x=3$ is a solution of $3 x^{2}+(k-1) x+9=0$; therefore, we have: $\begin{array}{l} 3(3)^{2}+(k-1) \times 3+9=0 \\ \Rightarrow 27+3(k-1)+9=0 \\ \Rightarrow...
Which of the following is not a quadratic equation?
(a)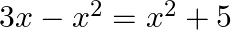 
(b) 
(c)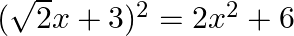 
(d)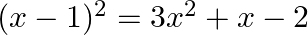 
Answer is (c) $(\sqrt{2} x+3)^{2}=2 x^{2}+6$ $\begin{array}{l} \because(\sqrt{2} x+3)^{2}=2 x^{2}+6 \\ \Rightarrow 2 x^{2}+9+6 \sqrt{2} x=2 x^{2}+6 \end{array}$ $\Rightarrow 6 \sqrt{2} x+3=0$, which...
The hypotenuse of a right-angled triangle is 1 meter less than twice the shortest side. If the third side 1 meter more than the shortest side, find the side, find the sides of the triangle.
Let the shortest side be $x \mathrm{~m}$. Therefore, according to the question: Hypotenuse $=(2 x-1) m$ Third side $=(x+1) m$ On applying Pythagoras theorem, we get: $\begin{array}{l} (2...
The hypotenuse of a right-angled triangle is 20 meters. If the difference between the lengths of the other sides be 4 meters, find the other sides
Let one side of the right-angled triangle be $x \mathrm{~m}$ and the other side be $(x+4) \mathrm{m}$. On applying Pythagoras theorem, we have: $\begin{array}{l} 20^{2}=(x+4)^{2}+x^{2} \\...
The area of right-angled triangle is 96 sq meters. If the base is three time the altitude, find the base.
Let the altitude of the triangle be $x \mathrm{~m}$. Therefore, the base will be $3 x \mathrm{~m}$. $\begin{array}{l} \text { Area of a triangle }=\frac{1}{2} \times \text { Base } \times \text {...
A farmer prepares rectangular vegetable garden of area 180 sq meters. With 39 meters of barbed wire, he can fence the three sides of the garden, leaving one of the longer sides unfenced. Find the dimensions of the garden.
Let the length and breadth of the rectangular garden be $x$ and $y$ meter, respectively. Given: $x y=180 \mathrm{sq} \mathrm{m}$$\ldots(i)$ and $\begin{array}{l} 2 y+x=39 \\ \Rightarrow x=39-2 y...
The sum of the areas of two squares is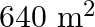 
. If the difference in their perimeter be 
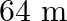, find the sides of the two square
Let the length of the side of the first and the second square be $x$ and $y \cdot$ respectively. According to the question: $x^{2}+y^{2}=640$ Also, $\begin{array}{l} 4 x-4 y=64 \\ \Rightarrow x-y=16...
The perimeter of a rectangular plot is 
and its area is 288 sq meters. Find the dimension of the plot
Let the length and breadth of the rectangular plot be $x$ and $y$ meter, respectively. Therefore, we have: $\begin{array}{l} \text { Perimeter }=2(x+y)=62 \quad \ldots . .(i) \text { and } \\ \text...
The length of a hall is 3 meter more than its breadth. If the area of the hall is 238 sq meters, calculate its length and breadth.
Let the breath of the rectangular hall be $x$ meter. Therefore, the length of the rectangular hall will be $(x+3)$ meter. According to the question: $\begin{array}{l} x(x+3)=238 \\ \Rightarrow...
Two water taps together can fill a tank in 6 hours. The tap of larger diameter takes 9 hours less than the smaller one to fill the tank separately. Find the time which each tap can separately fill the tank.
Let the tap of smaller diameter fill the tank in $x$ hours. $\therefore$ Time taken by the tap of larger diameter to fill the tank $=(x-9) h$ Suppose the volume of the tank be $V$. Volume of the...
Two pipes running together can fill a cistern in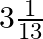 
minutes. If one pipe takes 3 minutes more than the other to fill it, find the time in which each pipe would fill the cistern.
Let one pipe fills the cistern in $x$ mins. Therefore, the other pipe will fill the cistern in $(x+3)$ mins. Time taken by both, running together, to fill the cistern $=3 \frac{1}{13} \min...
A motorboat whose speed is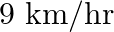 
in still water, goes 
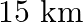downstream and comes back in a total time of 3 hours 45 minutes. Find the speed of the stream.
Let the speed of the stream be $x \mathrm{~km} / \mathrm{hr}$. $\therefore$ Downstream speed $=(9+x) \mathrm{km} / \mathrm{hr}$ Upstream speed $=(9-x) \mathrm{km} / \mathrm{hr}$ Distance covered...
A motor boat whose speed in still water is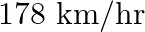 
, takes 1 hour more to go 
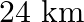upstream than to return to the same spot. Find the speed of the stream.
Let the speed of the stream be $x \mathrm{~km} / \mathrm{hr}$. Given: Speed of the boat $=18 \mathrm{~km} / \mathrm{hr}$ $\therefore$ Speed downstream $=(18+x) \mathrm{km} / h r$ Speed upstream...
A train covers a distance of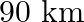 
at a uniform speed. Had the speed been 
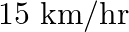more, it would have taken 30 minutes less for the journey. Find the original speed of the train.
Let the original speed of the train be $x \mathrm{~km} / \mathrm{hr}$. According to the question: $\frac{90}{x}-\frac{90}{(x+15)}=\frac{1}{2}$ $\begin{array}{l} \Rightarrow \frac{90(x+15)-90...
A train travels at a certain average speed for a distanced of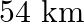 
and then travels a distance of 63 
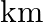at an average speed of 
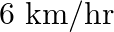more than the first speed. If it takes 3 hours to complete the total journey, what is its first speed?
Let the first speed of the train be $x \mathrm{~km} / \mathrm{h}$. Time taken to cover $54 \mathrm{~km}=\frac{54}{x} h .$ New speed of the train $=(x+6) \mathrm{km} / \mathrm{h}$ $\therefore$ Time...
A train covers a distance of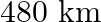 
at a uniform speed. If the speed had been 
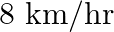less then it would have taken 3 hours more to cover the same distance. Find the usual speed of the train.
Let the usual speed of the train be $x \mathrm{~km} / \mathrm{h}$. $\therefore$ Reduced speed of the train $=(x-8) \mathrm{km} / \mathrm{h}$ Total distance to be covered $=480 \mathrm{~km}$ Time...
If one root of the equation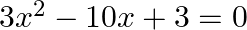 
is 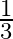then the other root is
(a)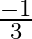
(b)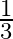
(c) -3
(d)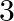 
Answer is (d)3 Given: $3 x^{2}-10 x+3=0$ One root of the equation is $\frac{1}{3}$. Let the other root be $\alpha$. Product of the roots $=\frac{c}{a}$ $\begin{array}{l} \Rightarrow \frac{1}{3}...
If the product of the roots of the equation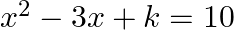 
is 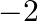then the value of 
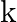is
(a)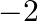
(b)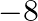 
(c) 8
(d) 12
Answer is (c) 8 It is given that the product of the roots of the equation $x^{2}-3 x+k=10$ is $-2$. The equation can be rewritten as: $x^{2}-3 x+(k-10)=0$ Product of the roots of a quadratic...
If one root of the equation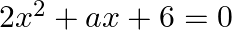 
is 2 then 
?
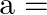(a) 7
(b)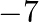 
(c)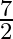 
(d)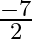 
Answer is (b) $-7$ It is given that one root of the equation $2 x^{2}+a x+6=0$ is 2 . $\begin{array}{l} \therefore 2 \times 2^{2}+a \times 2+6=0 \\ \Rightarrow 2 a+14=0 \\ \Rightarrow a=-7...
Which of the following is not a quadratic equation?
(a)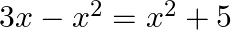
(b)
(c)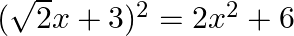
(d)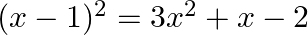
Answer is (c) $(\sqrt{2} x+3)^{2}=2 x^{2}+6$ $\begin{array}{l} \because(\sqrt{2} x+3)^{2}=2 x^{2}+6 \\ \Rightarrow 2 x^{2}+9+6 \sqrt{2} x=2 x^{2}+6 \end{array}$ $\Rightarrow 6 \sqrt{2} x+3=0$, which...
The area of right -angled triangle is 165 sq meters. Determine its base and altitude if the latter exceeds the former by 7 meters.
Let the base be $x \mathrm{~m}$. Therefore, the altitude will be $(x+7) m$. Area of a triangle $=\frac{1}{2} \times$ Base $\times$ Altitude $\begin{array}{l} \therefore \frac{1}{2} \times x...
The area of a right triangle is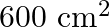 
. If the base of the triangle exceeds the altitude by 
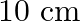, find the dimensions of the triangle.
Let the altitude of the triangle be $x \mathrm{~cm}$ Therefore, the base of the triangle will be $(x+10) \mathrm{cm}$ $\begin{array}{l} \text { Area of triangle }=\frac{1}{2} x(x+10)=600 \\...
The length of a rectangle is thrice as long as the side of a square. The side of the square is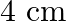 
more than the width of the rectangle. Their areas being equal, find the dimensions.
Let the breadth of rectangle be $x \mathrm{~cm}$. According to the question: Side of the square $=(x+4) \mathrm{cm}$ Length of the rectangle $=\{3(x+4)\} \mathrm{cm}$ It is given that the areas of...
A rectangular filed in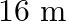 
long and 
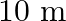wide. There is a path of uniform width all around it, having an area of 
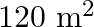. Find the width of the path
Let the width of the path be $x \mathrm{~m}$. $\therefore$ Length of the field including the path $=16+x+x=16+2 x$ Breadth of the field including the path $=10+x+x=10+2 x$ Now, (Area of the field...
The length of a hall is 3 meter more than its breadth. If the area of the hall is 238 sq meters, calculate its length and breadth.
Let the breath of the rectangular hall be $x$ meter. Therefore, the length of the rectangular hall will be $(x+3)$ meter. According to the question: $\begin{array}{l} x(x+3)=238 \\ \Rightarrow...
The length of rectangle is twice its breadth and its areas is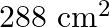 
. Find the dimension of the rectangle.
Let the length and breadth of the rectangle be $2 x \mathrm{~m}$ and $x \mathrm{~m}$, respectively. According to the question: $2 x \times x=288$ $\Rightarrow 2 x^{2}=288$ $\Rightarrow x^{2}=144$...
Two pipes running together can fill a tank in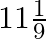 
minutes. If on pipe takes 5 minutes more than the other to fill the tank separately, find the time in which each pipe would fill the tank separately.
Let the time taken by one pipe to fill the tank be $x$ minutes. $\therefore$ Time taken by the other pipe to fill the tank $=(x+5) \min$ Suppose the volume of the tank be $V$. Volume of the tank...
A takes 10 days less than the time taken by 
to finish a piece of work. If both 
and together can finish the work in 12 days, find the time taken by to finish the work.
Let B takes $x$ days to complete the work. Therefore, A will take $(x-10)$ days. $\begin{array}{l} \therefore \frac{1}{x}+\frac{1}{(x-10)}=\frac{1}{12} \\ \Rightarrow...
The speed of a boat in still water is 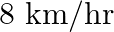. It can go 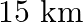upstream and 
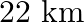downstream is 5 hours. Fid the speed of the stream
Speed of the boat in still water $=8 \mathrm{~km} / \mathrm{hr}$. Let the speed of the stream be $x \mathrm{~km} / \mathrm{hr}$. $\therefore$ Speed upstream $=(8-x) \mathrm{km} / \mathrm{hr}$ Speed...
The distance between Mumbai and Pune is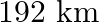 
. Travelling by the Deccan Queen, it takes 48 minutes less than another train. Calculate the speed of the Deccan Queen if the speeds of the two train differ by 
.
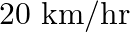Let the speed of the Deccan Queen be $x \mathrm{~km} / \mathrm{hr}$. According to the question: Speed of another train $=(x-20) \mathrm{km} / \mathrm{hr}$ $\begin{array}{l} \therefore...
A train covers a distance of 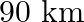at a uniform speed. Had the speed been 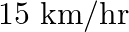more, it would have taken 30 minutes less for the journey. Find the original speed of the train.
Let the original speed of the train be $x \mathrm{~km} / \mathrm{hr}$. According to the question: $\frac{90}{x}-\frac{90}{(x+15)}=\frac{1}{2}$ $\begin{array}{l} \Rightarrow \frac{90(x+15)-90...
While boarding an aeroplane, a passengers got hurt. The pilot showing promptness and concern, made arrangements to hospitalize the injured and so the plane started late by 30 minutes. To reach the destination,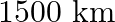 
away, in time, the pilot increased the speed by 
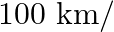hour. Find the original speed of the plane. Do you appreciate the values shown by the pilot, namely promptness in providing help to the injured and his efforts to reach in time?
Let the original speed of the plane be $x \mathrm{~km} / \mathrm{h}$. $\therefore$ Actual speed of the plane $=(x+100) \mathrm{km} / \mathrm{h}$ Distance of the journey $=1500 \mathrm{~km}$ Time...
The sum of the ages of a boy and his brother is 25 years, and the product of their ages in years is 126 . Find their ages.
Let the present ages of the boy and his brother be $x$ years and $(25-x)$ years. According to the question: $\begin{array}{l} x(25-x)=126 \\ \Rightarrow 25 x-x^{2}=126 \\ \Rightarrow x^{2}-(18-7)...
One year ago, man was 8 times as old as his son. Now, his age is equal to the square of his son’s age. Find their present ages.
Let the present age of the son be $x$ years. $\therefore$ Present age of the $\operatorname{man}=x^{2}$ years One year ago, Age of the son $=(x-1)$ years Age of the man $=\left(x^{2}-1\right)$ years...
A man buys a number of pens for Rs. 180 . If he had bought 3 more pens for the same amount, each pen would have cost him Rs. 3 less. How many pens did he buy?
Let the total number of pens be $x$. According to the question: $\begin{array}{l} \frac{80}{x}-\frac{80}{x+4}=1 \\ \Rightarrow \frac{80(x+4)-80 x}{x(x+4)}=1 \\ \Rightarrow \frac{80+320-80 x}{x^{2}+4...
A person on tour has Rs. 10800 for his expenses. If he extends his tour by 4 days, he has to cut down his daily expenses by Rs. 90 . Find the original duration of the tour.
Let the original duration of the tour be $x$ days. $\therefore \text { Original daily expenses }=\text { γ } \frac{10,800}{x}$ If he extends his tour by 4 days, then his new daily expenses...
The numerator of a fraction is 3 less than its denominator. If 1 is added to the denominator, the fraction is decreased by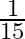 
. Find the fraction.
Let the denominator of the required fraction be $x$. Numerator of the required fraction $=x-3$ $\therefore$ Original fraction $=\frac{x-3}{x}$ If 1 is added to the denominator, then the new fraction...
A two-digit number is such that the product of its digits is 14 . If 45 is added to the number, the digit interchange their places. Find the number.
Let the digits at units and tens places be $x$ and $y$, respectively. $\therefore x y=14$ $\Rightarrow y=\frac{14}{x}$ According to the question: $\begin{array}{l} (10 y+x)+45=10 x+y \\ \Rightarrow...
Three consecutive positive integers are such that the sum of the square of the first and product of the other two is 46 . Find the integers.
Let the three consecutive positive integers be $x, x+1$ and $x+2$. According to the given condition, $\begin{array}{l} x^{2}+(x+1)(x+2)=46 \\ \Rightarrow x^{2}+x^{2}+3 x+2=46 \\ \Rightarrow 2...
Divide two natural numbers, the sum of whose squares is 25 times their sum and also equal to 50 times their difference.
Let the two natural numbers be $x$ and $y$. According to the question: $\begin{array}{l} x^{2}+y^{2}=25(x+y) \quad \ldots \ldots(i) \\ x^{2}+y^{2}=50(x-y) \end{array}$ From (i) and (ii), we get:...
Divide 27 into two parts such that the sum of their reciprocal is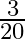 
.
Let the two parts be $x$ and $(27-x)$. According to the given condition, $\begin{array}{l} \frac{1}{x}+\frac{1}{27-x}=\frac{3}{20} \\ \Rightarrow \frac{27-x+x}{x(27-x)}=\frac{3}{20} \\ \Rightarrow...
The sum of natural number and its reciprocal is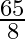 
. Find the number.
Let the natural number be $x$. According to the given condition, $\begin{array}{l} x+\frac{1}{x}=\frac{65}{8} \\ \Rightarrow \frac{x^{2}+1}{x}=\frac{65}{8} \\ \Rightarrow 8 x^{2}+8=65 x \\...
The difference of two natural numbers is 5 and the difference of heir reciprocals is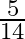 
. Find the numbers.
Let the required natural numbers be $x$ and $(x+5)$. Now, $x<x+5$ $\therefore \frac{1}{x}>\frac{1}{x+5}$ According to the given condition, $\begin{array}{l}...
The sum of two natural numbers is 15 and the sum of their reciprocals is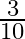 
. Find the numbers.
Let the required natural numbers be $x$ and $(15-x)$. According to the given condition, $\begin{array}{l} \frac{1}{x}+\frac{1}{15-x}=\frac{3}{10} \\ \Rightarrow \frac{15-x+x}{x(15-x)}=\frac{3}{10}...
Find the two consecutive positive even integers whose product is 288.
Let the two consecutive positive even integers be $x$ and $(x+2)$. According to the given condition, $\begin{array}{l} x(x+2)=288 \\ \Rightarrow x^{2}+2 x-288=0 \\ \Rightarrow x^{2}+18 x-16 x-288=0...
Find two consecutive multiples of 3 whose product is 648.
Let the required consecutive multiples of 3 be $3 x$ and $3(x+1)$. According to the given condition, $\begin{array}{l} 3 x \times 3(x+1)=648 \\ \Rightarrow 9\left(x^{2}+x\right)=648 \\ \Rightarrow...
The product of two consecutive positive integers is 306 . Find the integers.
Let the two consecutive positive integers be $x$ and $(x+1)$. According to the given condition, $\begin{array}{l} x(x+1)=306 \\ \Rightarrow x^{2}+x-306=0 \\ \Rightarrow x^{2}+18 x-17 x-306=0 \\...
The sum of the squares to two consecutive positive odd numbers is 514 . Find the numbers.
Let the two consecutive positive odd numbers be $x$ and $(x+2)$. According to the given condition, $\begin{array}{l} x^{2}+(x+2)^{2}=514 \\ \Rightarrow x^{2}+x^{2}+4 x+4=514 \\ \Rightarrow 2 x^{2}+4...
The sum of two natural number is 28 and their product is 192 . Find the numbers.
Let the required number be $x$ and $(28-x)$. According to the given condition, $\begin{array}{l} x(28-x)=192 \\ \Rightarrow 28 x-x^{2}=192 \\ \Rightarrow x^{2}-28 x+192=0 \\ \Rightarrow x^{2}-16...
The sum of natural number and its positive square root is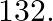 
Find the number.
Let the required natural number be $x$. According to the given condition, $x+\sqrt{x}=132$ Putting $\sqrt{x}=y$ or $x=y^{2}$, we get $y^{2}+y=132$ $\Rightarrow y^{2}+y-132=0$ $\Rightarrow y^{2}+12...
If the roots of the equations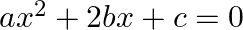 
and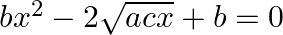 
are simultaneously real then prove that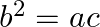 
It is given that the roots of the equation $a x^{2}+2 b x+c=0$ are real. $\begin{array}{l} \therefore D_{1}=(2 b)^{2}-4 \times a \times c \geq 0 \\ \Rightarrow 4\left(b^{2}-a c\right) \geq 0 \\...
Find the value of for which the roots of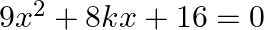 
are real and equal
Given: $\begin{array}{l} 9 x^{2}+8 k x+16=0 \\ \text { Here, } \\ a=9, b=8 k \text { and } c=16 \end{array}$ It is given that the roots of the equation are real and equal; therefore, we have:...
Find the value of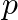 
for which the quadratic equation 
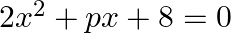has real roots.
$2 x^{2}+p x+8=0$ Here, $a=2, b=p$ and $c=8$ Discriminant $D$ is given by: $\begin{array}{l} D=\left(b^{2}-4 a c\right) \\ =p^{2}-4 \times 2 \times 8 \\ =\left(p^{2}-64\right) \end{array}$ If $D...
If 3 is a root of the quadratic equation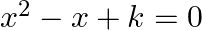 
., find the value of 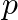so that the roots of the equation 
are equal.
It is given that 3 is a root of the quadratic equation $x^{2}-x+k=0$. $\begin{array}{l} \therefore(3)^{2}-3+k=0 \\ \Rightarrow k+6=0 \\ \Rightarrow k=-6 \end{array}$ The roots of the equation...
Find the values of 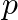for which the quadratic equation 
. , 
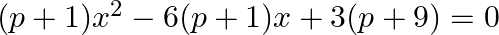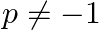has equal roots. Hence find the roots of the equation.
The given equation is $(p+1) x^{2}-6(p+1) x+3(p+9)=0$. This is of the form $a x^{2}+b x+c=0$, where $a=p+1, b=-6(p+1)$ and $c=3(p+9)$. $\begin{array}{l} \therefore D=b^{2}-4 a c \\ =[-6(p+1)]^{2}-4...
Find the values of 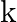for which the quadratic equation 
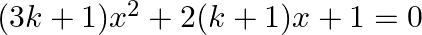. has real and equal roots.
The given equation is $(3 k+1) x^{2}+2(k+1) x+1=0$. This is of the form $a x^{2}+b x+c=0$, where $a=3 k+1, b=2(k+1)$ and $c=1$. $\begin{array}{l} \therefore D=b^{2}-4 a c \\ =[2(k+1)]^{2}-4 \times(3...
For what values of 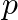are the roots of the equation 
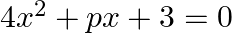. real and equal?
The given equation is $4 x^{2}+p x+3=0$. This is of the form $a x^{2}+b x+c=0$, where $a=4, b=p$ and $c=3$. $\therefore D=b^{2}-4 a c=p^{2}-4 \times 4 \times 3=p^{2}-48$ The given equation will have...
For what value of are the roots of the quadratic equation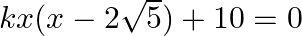 
real and equal.
The given equation is $\begin{array}{l} k x(x-2 \sqrt{5})+10=0 \\ \Rightarrow k x^{2}-2 \sqrt{5} k x+10=0 \end{array}$ This is of the form $a x^{2}+b x+c=0$, where $a=k, b=-2 \sqrt{5} k$ and $c=10$....
If a and b are distinct real numbers, show that the quadratic equations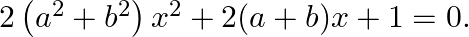 
has no real roots.
The given equation is $2\left(a^{2}+b^{2}\right) x^{2}+2(a+b) x+1=0$ $\begin{array}{l} \therefore D=[2(a+b)]^{2}-4 \times 2\left(a^{2}+b^{2}\right) \times 1 \\ =4\left(a^{2}+2 a...
Find the nature of roots of the following quadratic equations:
(i)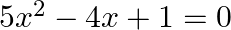 
(ii)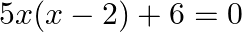 
(i) The given equation is $5 x^{2}-4 x+1=0$ This is of the form $a x^{2}+b x+c=0$, where $a=5, b=-4$ and $c=1$. $\therefore$ Discriminant, $D=b^{2}-4 a c=(-4)^{2}-4 \times 5 \times 1=16-20=-4<0$...
Find the roots of the each of the following equations, if they exist, by applying the quadratic formula: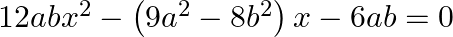 
, where 
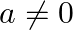and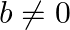 
$12 a b x^{2}-\left(9 a^{2}-8 b^{2}\right) x-6 a b=0$ On comparing it with $A x^{2}+B x+C=0$, we get: $A=12 a b, B=-\left(9 a^{2}-8 b^{2}\right)$ and $C=-6 a b$ Discriminant $D$ is given by:...
Find the roots of the each of the following equations, if they exist, by applying the quadratic formula: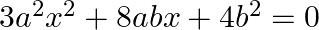 
$3 a^{2} x^{2}+8 a b x+4 b^{2}=0$ On comparing it with $A x^{2}+B x+C=0$, we get: $A=3 a^{2}, B=8 a b$ and $C=4 b^{2}$ Discriminant $D$ is given by: $\begin{array}{l} D=\left(B^{2}-4 A C\right) \\...
Find the roots of the each of the following equations, if they exist, by applying the quadratic formula: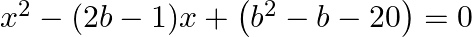 
.
The given equation is $x^{2}-(2 b-1) x+\left(b^{2}-b-20\right)=0$ Comparing it with $A x^{2}+B x+C=0$, we get $A=1, B=-(2 b-1)$ and $C=b^{2}-b-20$ $\therefore$ Discriminant, $D=B^{2}-4 A C=[-(2...
Find the roots of the each of the following equations, if they exist, by applying the quadratic formula: 
.
The given equation is $4 x^{2}-4 b x-\left(a^{2}-b^{2}\right)=0$ Comparing it with $A x^{2}+B x+C=0$, we get $A=4, B=4 b$ and $C=-\left(a^{2}-b^{2}\right)$ $\therefore$ Discriminant, $D=B^{2}-4 A...
Find the roots of the each of the following equations, if they exist, by applying the quadratic formula: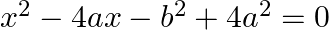 
.
The given equation is $x^{2}-4 a x-b^{2}+4 a^{2}=0$. Comparing it with $A x^{2}+B x+C=0$, we get $A=1, B=-4 a$ and $C=-b^{2}+4 a^{2}$ $\therefore$ Discriminant, $D=B^{2}-4 A C=(-4 a)^{2}-4 \times 1...
Find the roots of the each of the following equations, if they exist, by applying the quadratic formula: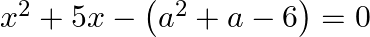 
.
The given equation is $x^{2}+5 x-\left(a^{2}+a-6\right)=0$. Comparing it with $A x^{2}+B x+C=0$, we get $A=1, B=5$ and $C=-\left(a^{2}+a-8\right)$ $\therefore$ Discriminant, $D=$ $\begin{array}{l}...
Find the roots of the each of the following equations, if they exist, by applying the quadratic formula: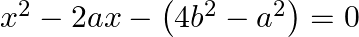 
The given equation is $x^{2}-2 a x-\left(4 b^{2}-a^{2}\right)=0$ Comparing it with $A x^{2}+B x+C=0$, we get $A=1, B=-2 a$ and $C=-\left(4 b^{2}-a^{2}\right)$ $\therefore$ Discriminant, $B^{2}-4 A...
Find the roots of the each of the following equations, if they exist, by applying the quadratic formula: 
The given equation is $\begin{array}{l} x-\frac{1}{x}=3, x \neq 0 \\ \Rightarrow \frac{x^{2}-1}{x}=3 \\ \Rightarrow x^{2}-1=3 x \\ \Rightarrow x^{2}-3 x-1=0 \end{array}$ This equation is of the form...
Find the roots of the each of the following equations, if they exist, by applying the quadratic formula: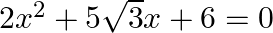 
.
The given equation is $2 x^{2}+5 \sqrt{3} x+6=0$. Comparing it with $a x^{2}+b x+c=0$, we get $a=2, b=5 \sqrt{3}$ and $c=6$ $\therefore$ Discriminant, $D=b^{2}-4 a c=(5 \sqrt{3})^{2}-4 \times 2...
Find the roots of the each of the following equations, if they exist, by applying the quadratic formula: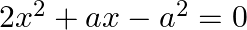 
.
The given equation is $2 x^{2}+a x-a^{2}=0$ Comparing it with $A x^{2}+B x+C=0$, we get $A=2, B=a$ and $C=-a^{2}$ $\therefore$ Discriminant, $D=B^{2}-4 A C=a^{2}-4 \times 2 \times-a^{2}=a^{2}+8...
Find the roots of the each of the following equations, if they exist, by applying the quadratic formula: 
The given equation is $2 \sqrt{3} x^{2}-5 x+\sqrt{3}=0$ Comparing it with $a x^{2}+b x+c=0$, we get $a=2 \sqrt{3}, b=-5$ and $c=\sqrt{3}$ $\therefore$ Discriminant, $D=b^{2}-4 a c=(-5)^{2}-4 \times...
Find the roots of the each of the following equations, if they exist, by applying the quadratic formula: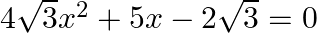 
The given equation is $4 \sqrt{3} x^{2}+5 x-2 \sqrt{3}=0$ Comparing it with $a x^{2}+b x+c=0$, we get $a=4 \sqrt{3}, b=5$ and $c=-2 \sqrt{3}$ $\therefore$ Discriminant, $D=b^{2}-4 a c=5^{2}-4 \times...
Find the roots of the each of the following equations, if they exist, by applying the quadratic formula: 
The given equation is $\sqrt{2} x^{2}+7+5 \sqrt{2}=0$. Comparing it with $a x^{2}+b x+c=0$, we get $a=\sqrt{2}, b=7$ and $c=5 \sqrt{2}$ $\therefore$ Discriminant, $D=b^{2}-4 a c=(7)^{2}-4 \times...
Find the roots of the each of the following equations, if they exist, by applying the quadratic formula: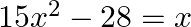 
Given: $\begin{array}{l} 15 x^{2}-28=x \\ \Rightarrow 15 x^{2}-x-28=0 \end{array}$ On comparing it with $a x^{2}+b x+c=0$, we get; $a=25, b=-1$ and $c=-28$ Discriminant $D$ is given by:...
Find the roots of the each of the following equations, if they exist, by applying the quadratic formula: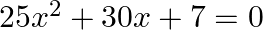 
Given: $25 x^{2}+30 x+7=0$ On comparing it with $a x^{2}+b x+x=0$, we get; $a=25, b=30$ and $c=7$ Discriminant $D$ is given by: $\begin{array}{l} D=\left(b^{2}-4 a c\right) \\ =30^{2}-4 \times 25...
Find the discriminant of the given equation: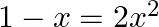 
$\begin{array}{l} 1-x=2 x^{2} \\ \Rightarrow 2 x^{2}+x-1=0 \end{array}$ Here, $\begin{array}{l} a=2 \\ b=1, \\ c=-1 \end{array}$ Discriminant $D$ is given by: $\begin{array}{l} D=b^{2}-4 a c \\...
Find the discriminant of the given equation: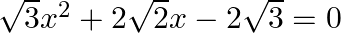 
Here, $\begin{aligned} a &=\sqrt{3} \\ b &=2 \sqrt{2} \\ c &=-2 \sqrt{3} \end{aligned}$ Discriminant $D$ is given by: $\begin{array}{l} D=b^{2}-4 a c \\ =(2 \sqrt{2})^{2}-4 \times...
Find the discriminant of the given equation: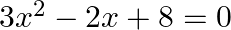 
Here, $a=3$ $b=-2$ $c=8$ Discriminant $D$ is given by: $D=b^{2}-4 a c$ $=(-2)^{2}-4 \times 3 \times 8$ $=4-96$ $=-92$
Find the roots of the given equation: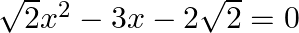 
$\sqrt{2} x^{2}-3 x-2 \sqrt{2}=0$ $\Rightarrow 2 x^{2}-3 \sqrt{2} x-4=0 \quad$ (Multiplying both sides by $\sqrt{2}$ ) $\Rightarrow 2 x^{2}-3 \sqrt{2} x=4$ $\Rightarrow(\sqrt{2} x)^{2}-2 \times...
Find the roots of the given equation: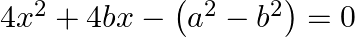
$\begin{array}{l} 4 x^{2}+4 b x-\left(a^{2}-b^{2}\right)=0 \\ \Rightarrow 4 x^{2}+4 b x=a^{2}-b^{2} \\ \Rightarrow(2 x)^{2}+2 \times 2 x \times b+b^{2}=a^{2}-b^{2}+b^{2} \text { (Adding } b^{2}...
Find the roots of the given equation: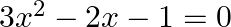 
$3 x^{2}-2 x-1=0$ $\Rightarrow 9 x^{2}-6 x-3=0 \quad$ (Multiplying both sides by 3) $\Rightarrow 9 x^{2}-6 x=3$ $\Rightarrow(3 x)^{2}-2 \times 3 x \times 1+1^{2}=3+1^{2} \quad$ [Adding $1^{2}$ on...
Find the roots of the given equation: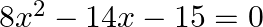 
$8 x^{2}-14 x-15=0$ $\Rightarrow 16 x^{2}-28 x-30=0 \quad$ (Multiplying both sides by 2) $\Rightarrow 16 x^{2}-28 x=30$ $\Rightarrow(4 x)^{2}-2 \times 4 x \times...
Find the roots of the given equation: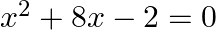 
$\begin{array}{l} x^{2}+8 x-2=0 \\ \Rightarrow x^{2}+8 x=2 \\ \Rightarrow x^{2}+2 \times x \times 4+4^{2}=2+4^{2} \\ \Rightarrow(x+4)^{2}=2+16=18 \\ \Rightarrow x+4=\pm \sqrt{18}=\pm 3 \sqrt{2} \\...
Find the roots of the given equation: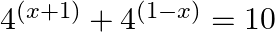 
Given: $\begin{array}{l} 4^{(x+1)}+4^{(1-x)}=10 \\ \Rightarrow 4^{x} \cdot 4+4^{1} \cdot \frac{1}{4^{4}}=10 \end{array}$ Let $4^{x}$ be $y$. $\begin{array}{l} \therefore 4 y+\frac{4}{y}=10 \\...
Find the roots of the given equation: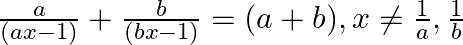 
$\begin{array}{l} \frac{a}{(a x-1)}+\frac{b}{(b x-1)}=(a+b) \\ \Rightarrow\left[\frac{a}{(a x-1)}-b\right]+\left[\frac{b}{(b x-1)}-a\right]=0 \\ \Rightarrow \frac{a-b(a x-1)}{a x-1}+\frac{b-a(b...
Find the roots of the given equation: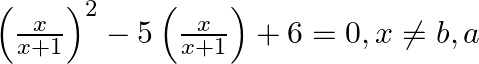 
$\left(\frac{x}{x+1}\right)^{2}-5\left(\frac{x}{x+1}\right)+6=0$ Putting $\frac{x}{x+1}=y$, we get: $\begin{array}{l} y^{2}-5 y+6=0 \\ \Rightarrow y^{2}-5 y+6=0 \end{array}$ $\begin{array}{l}...
Find the roots of the given equation: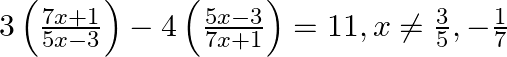 
$\begin{array}{l} 3\left(\frac{7 x+1}{5 x-3}\right)-4\left(\frac{5 x-3}{7 x+1}\right)=11, x \neq \frac{3}{5},-\frac{1}{7} \\ \Rightarrow \frac{3(7 x+1)^{2}-4(5 x-3)^{2}}{(5 x-3)(7 x+1)}=11 \\...
Find the roots of the given equation: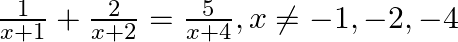 
$\begin{array}{l} \frac{1}{x+1}+\frac{2}{x+2}=\frac{5}{x+4}, x \neq-1,-2,-4 \\ \Rightarrow \frac{x+2+2 x+2}{(x+1)(x+2)}=\frac{5}{x+4} \\ \Rightarrow \frac{3 x+4}{x^{2}+3 x+2}=\frac{5}{x+4} \\...
Find the roots of the given equation: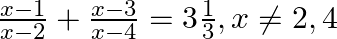 
$\begin{array}{l} \frac{x-1}{x-2}+\frac{x-3}{x-4}=3 \frac{1}{3}, x \neq 2,4 \\ \Rightarrow \frac{(x-1)(x-4)+(x-2)(x-3)}{(x-2)(x-4)}=\frac{10}{3} \\ \Rightarrow \frac{x^{2}-5 x+4+x^{2}-5 x+6}{x^{2}-6...
Find the roots of the given equation: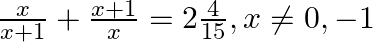 
$\begin{array}{l} \frac{x}{x+1}+\frac{x+1}{x}=2 \frac{4}{15}, x \neq 0,-1 \\ \Rightarrow \frac{x^{2}+(x+1)^{2}}{x(x+1)}=\frac{34}{15} \\ \Rightarrow \frac{x^{2}+x^{2}+2 x+1}{x^{2}+x}=\frac{34}{15}...
Find the roots of the given equation: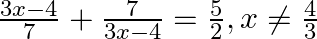 
$\begin{array}{l} \frac{3 x-4}{7}+\frac{7}{3 x-4}=\frac{5}{2}, x \neq \frac{4}{3} \\ \Rightarrow \frac{(3 x-4)^{2}+49}{7(3 x-4)}=\frac{5}{2} \end{array}$ $\begin{array}{l} \Rightarrow \frac{9...
Find the roots of the given equation: 57.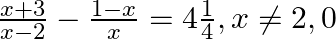 
$\begin{array}{l} \frac{(x+3)}{(x-2)}-\frac{(1-x)}{x}=\frac{17}{4} \\ \Rightarrow \frac{x(x+3)-(1-x)(x-2)}{(x-2) x}=\frac{17}{4} \\ \Rightarrow \frac{x^{2}+3 x-\left(x-2-x^{2}+2 x\right)}{x^{2}-2...
Find the roots of the given equation: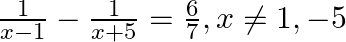 
$\begin{array}{l} \frac{1}{x-1}-\frac{1}{x+5}=\frac{6}{7}, x \neq 1,-5 \\ \Rightarrow \frac{x+5-x+1}{(x-1)(x+5)}=\frac{6}{7} \\ \Rightarrow \frac{6}{x^{2}+4 x-5}=\frac{6}{7} \\ \Rightarrow x^{2}+4...
Find the roots of the given equation: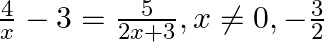 
$\begin{array}{l} \frac{4}{x}-3=\frac{5}{2 x+3}, x \neq 0,-\frac{3}{2} \\ \Rightarrow \frac{4}{x}-\frac{5}{2 x+3}=3 \\ \Rightarrow \frac{8 x+12-5 x}{x(2 x+3)}=3 \\ \Rightarrow \frac{3 x+12}{2...
Find the roots of the given equation: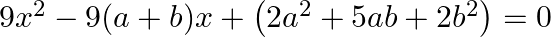 
We write, $-9(a+b) x=-3(2 a+b) x-3(a+2 b) x$ as $\begin{array}{l} 9 x^{2} \times\left(2 a^{2}+5 a b+2 b^{2}\right)=9\left(2 a^{2}+5 a b+2 b^{2}\right) x^{2}=[-3(2 a+b) x] \times[-3(a+2 b) x] \\...
Find the roots of the given equation: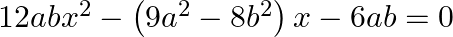
$\begin{array}{l} 12 a b x^{2}-\left(9 a^{2}-8 b^{2}\right) x-6 a b=0 \\ \Rightarrow 12 a b x^{2}-9 a^{2} x+8 b^{2} x-6 a b=0 \\ \Rightarrow 3 a x(4 b x-3 a)+2 b(4 b x-3 a)=0 \\ \Rightarrow(3 a x+2...
Find the roots of the given equation: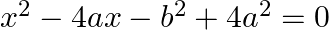
We write, $-4 a x=-(b+2 a) x+(b-2 a) x$ as $\begin{array}{l} x^{2} \times\left(-b^{2}+4 a^{2}\right)=\left(-b^{2}+4 a^{2}\right) x^{2}=-(b+2 a) x \times(b-2 a) x \\ \therefore x^{2}-4 a x-b^{2}+4...
Find the roots of the given equation: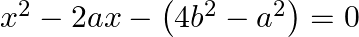
We have, $-2 a x=(2 b-a) x-(2 b+a) x$ as $\begin{array}{l} x^{2} \times\left[-\left(4 b^{2}-a^{2}\right)\right]=-\left(4 b^{2}-a^{2}\right) x^{2}=(2 b-a) x \times[-(2 b+a) x] \\ \therefore x^{2}-2 a...
Find the roots of the given equation: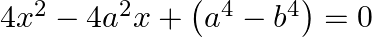 
We write, $-4 a^{2} x=-2\left(a^{2}+b^{2}\right) x-2\left(a^{2}-b^{2}\right) x$ as $\begin{array}{l} 4 x^{2} \times\left(a^{4}-b^{4}\right)=4\left(a^{4}-b^{4}\right)...
Find the roots of the given equation: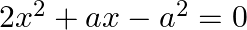
We write, $a x=2 a x-a x$ as $2 x^{2} \times\left(-a^{2}\right)=-2 a^{2} x^{2}=2 a x \times(-a x)$ $\begin{array}{l} \therefore 2 x^{2}+a x-a^{2}=0 \\ \Rightarrow 2 x^{2}+2 a x-a x-a^{2}=0 \\...
Find the roots of the given equation: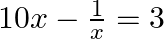 
$\begin{array}{l} 10 x-\frac{1}{x}=3 \\ \Rightarrow 10 x^{2}-1=3 x \end{array}$ [Multiplying both sides by $x]$ $\begin{array}{l} \Rightarrow 10 x^{2}-3 x-1=0 \\ \Rightarrow 10 x^{2}-(5 x-2 x)-1=0...
Find the roots of the given equation: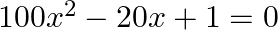 
We write, $-20 x=-10 x-10 x$ as $100 x^{2} \times 1=100 x^{2}=(-10 x) \times(-10 x)$ $\begin{array}{l} \therefore 100 x^{2}-20 x+1=0 \\ \Rightarrow 100 x^{2}-10 x-10 x+1=0 \end{array}$...
Find the roots of the given equation: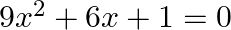 
$\begin{array}{l} 9 x^{2}+6 x+1=0 \\ \Rightarrow 9 x^{2}+3 x+3 x+1=0 \\ \Rightarrow 3 x(3 x+1)+1(3 x+1)=0 \\ \Rightarrow(3 x+1)(3 x+1)=0 \\ \Rightarrow 3 x+1=0 \text { or } 3 x+1=0 \\ \Rightarrow...
Find the roots of the given equation: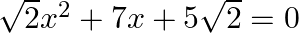 
We write, $7 x=5 x+2 x$ as $\sqrt{2} x^{2} \times 5 \sqrt{2}=10 x^{2}=5 x \times 2 x$ $\begin{array}{l} \therefore \sqrt{2} x^{2}+7 x+5 \sqrt{2}=0 \\ \Rightarrow \sqrt{2} x^{2}+5 x+2 x+5 \sqrt{2}=0...
Find the roots of the given equation: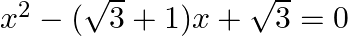
$\begin{array}{l} x^{2}-(\sqrt{3}+1) x+\sqrt{3}=0 \\ \Rightarrow x^{2}-\sqrt{3} x-x+\sqrt{3}=0 \\ \Rightarrow x(x-\sqrt{3})-1(x-\sqrt{3})=0 \\ \Rightarrow(x-\sqrt{3})(x-1)=0 \\ \Rightarrow...
Find the roots of the given equation: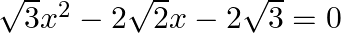
We write, $-2 \sqrt{2} x=-3 \sqrt{2} x+\sqrt{2} x$ as $\sqrt{3} x^{2} \times(-2 \sqrt{3})=-6 x^{2}=(-3 \sqrt{2} x) \times(\sqrt{2} x)$ $\therefore \sqrt{3} x^{2}-2 \sqrt{2} x-2 \sqrt{3}=0$...
Find the roots of the given equation: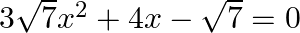 
$\begin{array}{l} 3 \sqrt{7} x^{2}+4 x-\sqrt{7}=0 \\ \Rightarrow 3 \sqrt{7} x^{2}+7 x-3 x-\sqrt{7}=0 \\ \Rightarrow \sqrt{7} x(3 x+\sqrt{7})-1(3 x+\sqrt{7})=0 \\ \Rightarrow(3...
Find the roots of the given equation: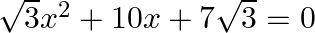 
We write: $10 x=3 x+7 x$ as $\sqrt{3} x^{2} \times 7 \sqrt{3}=21 x^{2}=3 x \times 7 x$ $\begin{array}{l} \therefore \sqrt{3} x^{2}+10 x+7 \sqrt{3}=0 \\ \Rightarrow \sqrt{3} x^{2}+3 x+7 x+7...
Find the roots of the given equation: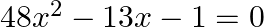 
$\begin{array}{l} 48 x^{2}-13 x-1=0 \\ \Rightarrow 48 x^{2}-(16 x-3 x)-1=0 \\ \Rightarrow 48 x^{2}-16 x+3 x-1=0 \\ \Rightarrow 16 x(3 x-1)+1(3 x-1)=0 \\ \Rightarrow(16 x+1)(3 x-1)=0 \\ \Rightarrow...
Find the roots of the given equation: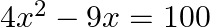 
$\begin{array}{l} 4 x^{2}-9 x=100 \\ \Rightarrow 4 x^{2}-9 x-100=0 \\ \Rightarrow 4 x^{2}-(25 x-16 x)-100=0 \\ \Rightarrow 4 x^{2}-25 x+16 x-100=0 \\ \Rightarrow x(4 x-25)+4(4 x-25)=0 \\...
Find the roots of the given equation: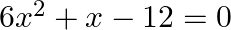 
.
$\begin{array}{l} 6 x^{2}+x-12=0 \\ \Rightarrow 6 x^{2}+9 x-8 x-12=0 \\ \Rightarrow 3 x(2 x+3)-4(2 x+3)=0 \\ \Rightarrow(3 x-4)(2 x+3)=0 \\ \Rightarrow 3 x-4=0 \text { or } 2 x+3=0 \\ \Rightarrow...
Find the roots of the given equation: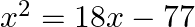 
$\begin{array}{l} x^{2}=18 x-77 \\ \Rightarrow x^{2}-18 x+77=0 \end{array}$ $\begin{array}{l} \Rightarrow x^{2}-(11 x+7 x)+77=0 \\ \Rightarrow x^{2}-11 x-7 x+77=0 \\ \Rightarrow x(x-11)-7(x-11)=0 \\...
Find the roots of the given equation: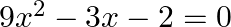 
.
We write, $-3 x=3 x-6 x$ as $9 x^{2} \times(-2)=-18 x^{2}=3 x \times(-6 x)$ $\begin{array}{l} \therefore 9 x^{2}-3 x-2=0 \\ \Rightarrow 9 x^{2}+3 x-6 x-2=0 \\ \Rightarrow 3 x(3 x+1)-2(3 x+1)=0 \\...
Find the roots of the given equation: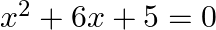 
We write, $6 x=x+5 x$ as $x^{2} \times 5=5 x^{2}=x \times 5 x$ $\begin{array}{l} \therefore x^{2}+6 x+5=0 \\ \Rightarrow x^{2}+x-5 x+5=0 \end{array}$ $\begin{array}{l} \Rightarrow x(x+1)+5(x+1)=0 \\...
Find the roots of the given equation: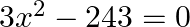 
$\begin{array}{l} 3 x^{2}-243=0 \\ \Rightarrow 3\left(x^{2}-81\right)=0 \\ \Rightarrow(x)^{2}-(9)^{2}=0 \\ \Rightarrow(x+9)(x-9)=0 \\ \Rightarrow x+9=0 \text { or } x-9=0 \\ \Rightarrow x=-9 \text {...
Find the value of for which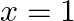 
is a root of the equation 
.
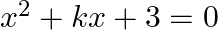It is given that $(x=1)$ is a root of $\left(x^{2}+k x+3=0\right)$. As a result, $(x=1)$ must satisfy the equation. $\begin{array}{l} \Rightarrow(1)^{2}+k \times 1+3=0 \\ \Rightarrow k+4=0 \\...
Which of the following are quadratic equation in 
?
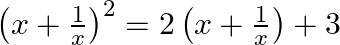
$\left(x+\frac{1}{x}\right)^{2}=2\left(x+\frac{1}{x}\right)+3$ $\begin{array}{l} \Rightarrow\left(\frac{x^{2}+1}{x}\right)^{2}=2\left(\frac{x^{2}+1}{x}\right)+3 \\...
Which of the following are quadratic equation in ?
(i)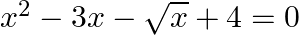 
(ii)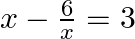 
(i) $\left(x^{2}-3 x-\sqrt{x}+4\right)$ contains a term with $\sqrt{x}$, i.e., $x^{\frac{1}{2}}$, where $\frac{1}{2}$ is not a integer. Therefore, it is not a quadratic polynomial. $\therefore...
10. Solve the following equation:
$10x – 1/x = 3$ Solution:- $10x – 1/x = 3$ $(10x-1)/x=3$ By cross multiplication we get, $10{{x}^{2}}-1=3x$ $10{{x}^{2}}-3x-1=0$ Divided by $10$ for both side of eachterm we get,...
15. Solve the following equation: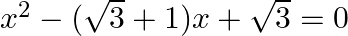
Solution: - ${{x}^{2}}-(\sqrt{3}+1)x+\sqrt{3}=0$ ${{x}^{2}}-\sqrt{3x}-x+\sqrt{3}=0$ Take out common in each term, $x(x-\sqrt{3})-1(x-\sqrt{3})=0$ $(x-\sqrt{3})(x-1)=0$ Equate both to zero, ...
14. Solve the following equation: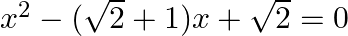
Solution: - ${{x}^{2}}-(\sqrt{2}+1)x+\sqrt{2}=0$ ${{x}^{2}}-x-\sqrt{2}x+\sqrt{2}=0$ Take out common in each term, $x(x-1)-\sqrt{2}(x-1)=0$ $(x-1)(x-\sqrt{2})=0$ Equate both to zero,...
13. Solve the following equation: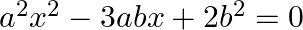
Solution: - ${{a}^{2}}{{x}^{2}}-3abx+2{{b}^{2}}=0$ Divided by${{a}^{2}}$ for both side of each term we get, ${{a}^{2}}{{x}^{2}}/{{a}^{2}}-3abx/{{a}^{2}}+2{{b}^{2}}/{{a}^{2}}=0$...
12. Solve the following equation: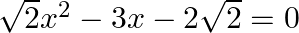
Solution: - $\sqrt{2}{{x}^{2}}-3x-2\sqrt{2}$ Divided by $\sqrt{2}$for both side of each term we get, $\sqrt{2}{{x}^{2}}/\sqrt{2}-3x/\sqrt{2}-2\sqrt{2}/\sqrt{2}=0$ ${{x}^{2}}-3x/\sqrt{2}-2=0$...
11. Solve the following equation: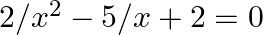
Solution: - $2/{{x}^{2}}-5{{x}^{2}}/x+2{{x}^{2}}=0$ Multiply by ${{x}^{2}}$for both side of each term we get, $2{{x}^{2}}/{{x}^{2}}-5{{x}^{2}}/x+2{{x}^{2}}=0$ $2-5x+2{{x}^{2}}=0$ Above equation can...
9. Solve the following equation:
$25x(x+1)=-4$ Solution:- $25x(x + 1) = -4$ Divided by \[25\]for both side of each term we get, \[25{{x}^{2}}/25\text{ }+\text{ }25x/25\text{ }=\text{ }\text{ }4/25\] \[{{x}^{2}}~+\text{ }x\text{...
8. Solve the following:
\[\mathbf{3}{{\mathbf{x}}^{\mathbf{2}}}~+\text{ }\mathbf{25x}\text{ }+\text{ }\mathbf{42}\text{ }=\text{ }\mathbf{0}\] Solution:- \[3{{x}^{2}}~+\text{ }25x\text{ }+\text{ }42\text{ }=\text{...
7. Solve the following equation:
\[\mathbf{4}{{\mathbf{x}}^{\mathbf{2}}}~-\text{ }\mathbf{13x}\text{ }-\text{ }\mathbf{12}\text{ }=\text{ }\mathbf{0}\] Solution:- \[4{{x}^{2}}~-13x\text{ }-12\text{ }=\text{ }0\] Divided by \[4\]for...
6. Solve the following question:
\[\mathbf{5}{{\mathbf{x}}^{\mathbf{2}}}~-\mathbf{11x}\text{ }+\text{ }\mathbf{2}\text{ }=\text{ }\mathbf{0}\] Solution:- \[5{{x}^{2}}~-\text{ }11x\text{ }+\text{ }2\text{ }=\text{ }0\]...
5. Solve the following equation:
\[\mathbf{2}{{\mathbf{x}}^{\mathbf{2}}}~-\text{ }\mathbf{x}\text{ }-\text{ }\mathbf{6}\text{ }=\text{ }\mathbf{0}\] Solution:- \[2{{x}^{2}}~-x\text{ }-\text{ }6\text{ }=\text{ }0~~~~~~\] Divided by...
4. Solve the following equation
\[\mathbf{2}{{\mathbf{x}}^{\mathbf{2}}}-\mathbf{3x}-\mathbf{9}\text{ }=\text{ }\mathbf{0}\] Solution:- \[2{{x}^{2}}-3x-9\text{ }=\text{ }0\] Divided by \[2\]for both side of each term we get,...
3. Solve the following equation:
\[\mathbf{4}{{\mathbf{x}}^{\mathbf{2}}}~+\text{ }\mathbf{16x}\text{ }=\text{ }\mathbf{0}~~~~~~\] Solution:- \[\mathbf{4}{{\mathbf{x}}^{\mathbf{2}}}~+\text{ }\mathbf{16x}\text{ }=\text{...
2. Solve the following equation:
$(2x + 3) (3x – 7) = 0$ Solution:- $(2x + 3) (3x – 7) = 0$ Equate both to zero, $(2x + 3) = 0, (3x – 7) = 0$ $2x = -3$, $3x = 7$ $x = -3/2$ Or $x = 7/3$
1. Solve the following equation:
$(x – 8) (x + 6) = 0$ Solution:- $(x – 8) (x + 6) = 0$ Equate both to zero, $(x – 8) = 0, (x + 6) = 0$ $x = 8$ or $x =...
1. The sum of the square of the 2 consecutive natural numbers is 481. Find the numbers.
Solution:- 1. The sum of the square of the 2 consecutive natural numbers is 481. Find the numbers. Solution:- let us assume the two consecutive number be \[P\] and \[P\text{ }+\text{ }1\] As per the...