A long straight cable of length
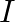
is placed symmetrically along the z-axis and has radius
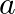
. The cable consists of a thin wire and a co-axial conducting tube. An alternating current
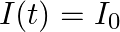
sin
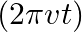
flows down the central thin wire and returns along the co-axial conducting tube. The induced electric field at a distance
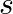
from the wire inside the cable is
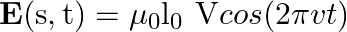
. In
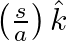
,
a) calculate the displacement current density inside the cable
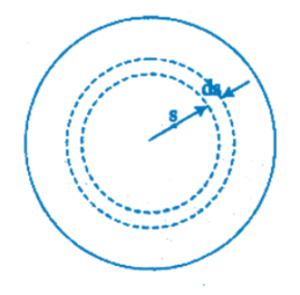
b) integrate the displacement current density across the cross-section of the cable to find the total displacement current I
![]()
![]()
![]()
![]()
![]()
![]()
