Login/Sign Up
Home » An air chamber of volume V has a neck area of cross-section into which a ball of mass just fits and can move up and down without any friction. Show that when the ball is pressed down a little and released, it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Figure]
An air chamber of volume V has a neck area of cross-section into which a ball of mass m just fits and can move up and down without any friction. Show that when the ball is pressed down a little and released, it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Figure]
CBSE | Class 11 | NCERT | Oscillations | Physics
An air chamber of volume V has a neck area of cross-section into which a ball of mass m just fits and can move up and down without any friction. Show that when the ball is pressed down a little and released, it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Figure]

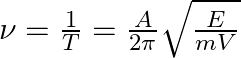
Solution:

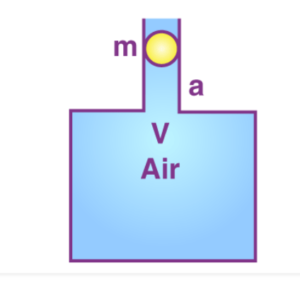
Volume of the air chamber is given as \mathrm{V}

Cross-sectional area of the neck is given as \mathrm{A}

Mass of the ball be m

The ball is fitted in the neck at position given as \mathrm{C}

The atmospheric pressure is equal to the pressure of the air beneath the ball in the chamber.

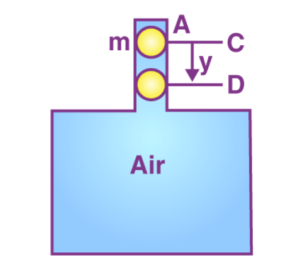
By raising the pressure by a little amount p, the ball is pressed down to position D.

Increase the pressure on the ball by a small amount p until the ball reaches position D.

The distance C D=y

The air chamber’s volume shrinks while the pressure rises.

The volume of air inside the chamber will decrease, resulting in an increase in pressure. \Delta V= Ay is the reduction in volume of air inside the chamber.

Volumetric strain = change in volume/ original volume

=\Delta \mathrm{V} / \mathrm{V}=\mathrm{A} y / \mathrm{N}

Bulk Modulus of elasticity, \mathrm{B}=\mathrm{S} tress/ volumetric strain

=-p /(A y / N)

=-p V / A y

p=-B A y / N

The restoring force on the ball due to the excess pressure

F=p \times A=(-B A y / N) \times A=-\left(B A^{2} / V\right) \cdot y

The negative sign in F \propto y shows that the force is directed toward the equilibrium position.

If the increased pressure is removed, the ball will move in the neck of the chamber in a simple harmonic motion, with C being the mean position.

In S.H.M., the restoring force, \mathrm{F}=-\mathrm{ky}

Comparing (1) and (2),

-k y=-\left(B A^{2} N\right) \cdot y

\mathrm{k}=\left(\mathrm{BA}^{2} \mathrm{~N}\right)

Inertia factor = mass of ball =\mathrm{m}

Time period, T=2 \pi \sqrt{\text { inertia factor } / \sqrt{\text { spring factor }}}

\mathrm{T}=2 \pi \sqrt{\mathrm{m}} / \sqrt{\mathrm{k}}

T=2 \pi \sqrt{\frac{m}{\frac{m}{V}^{2}}}=\frac{2 \pi}{A} \sqrt{\frac{m V}{E}}

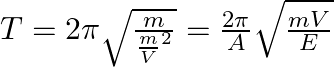
Frequency, \nu=\frac{1}{T}=\frac{A}{2 \pi} \sqrt{\frac{E}{m V}}

 

i

More Material