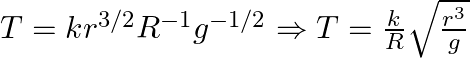Kepler’s third law states that,
![]() i.e., square of time period
i.e., square of time period ![]() of a satellite revolving around a planet, is proportional to the cube of the radius of the orbit
of a satellite revolving around a planet, is proportional to the cube of the radius of the orbit ![]() .
.
On applying Kepler’s third law,
![]()
Also, ![]() depends on
depends on ![]() and
and ![]() .
.
Let ![]()
![]() …..(i)
…..(i)
where,
![]() dimensionless constant.
dimensionless constant.
On writing the dimensions of various quantities on both the sides, we get
![Rendered by QuickLaTeX.com \begin{aligned} \left[M^{0} L^{0} T\right] &=[L]^{3 / 2}\left[L T^{-2}\right]^{a}[L]^{b} \\ &=\left[M^{0} L^{a+b+3 / 2} T^{-2 a}\right] \end{aligned}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-ecd102f02dc42a7d416be601278a6b60_l3.png)
Comparing the dimensions of both sides,
![]() …..(ii)
…..(ii)
![]() …..(iii)
…..(iii)
From Eq. (ii), we get
![]()
Putting the values of ![]() and
and ![]() in Eq. (i), we get
in Eq. (i), we get