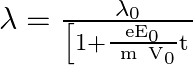Answer is (3)
Initial de-broglie wavelength will be,
![]() …(i)
…(i)
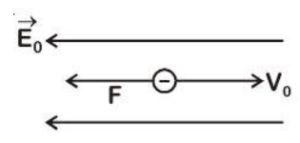
Acceleration of electron will be,
![]()
Velocity after time t,
![]()
So, 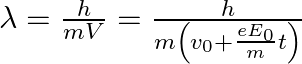
![Rendered by QuickLaTeX.com =\frac{h}{m V_{0}\left[1+\frac{e E_{0}}{m V_{0}} t\right]}=\frac{\lambda_{0}}{\left[1+\frac{e E_{0}}{m V_{0}} t\right]}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-318b4b2b72f4e4380b759b6a4b38081f_l3.png) …(ii)
…(ii)
Divide (ii) by (i) we get,
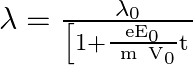
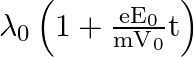
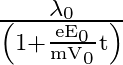
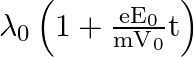
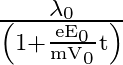
Answer is (3)
Initial de-broglie wavelength will be,
![]() …(i)
…(i)

Acceleration of electron will be,
![]()
Velocity after time t,
![]()
So, 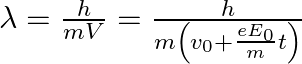
![Rendered by QuickLaTeX.com =\frac{h}{m V_{0}\left[1+\frac{e E_{0}}{m V_{0}} t\right]}=\frac{\lambda_{0}}{\left[1+\frac{e E_{0}}{m V_{0}} t\right]}](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-318b4b2b72f4e4380b759b6a4b38081f_l3.png) …(ii)
…(ii)
Divide (ii) by (i) we get,