Solution:
(i)
As per the question,
It is known that the value of ![]() lies between
lies between ![]()
![]()
Multiply by negative sign, we have
Or ![]()
When we add 1, we have
![]() (i)
(i)
So now,
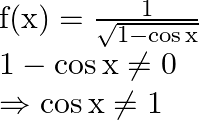
Or, ![]()
As a result, the domain of ![]()
(ii)
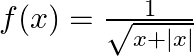
As per the question,
For real value of ![]() ,
,
![]()
When ![]()
![]()
When ![]()
![]()
Therefore, ![]() , to satisfy the provided equation.
, to satisfy the provided equation.
As a result, the domain of ![]()
